WKPowerMeans多径簇识别算法

杨晋生，吴旭曌

WKPowerMeans多径簇识别算法

杨晋生，吴旭曌

(天津大学电子信息工程学院，天津 300072)

针对KPowerMeans聚类算法多径散射簇的估计过程复杂及聚类结果高度依赖随机初始簇中心的问题，提出了一种改进的多径簇识别算法——WKPowerMeans算法．首先利用小波变换的尖峰检测技术估计出多径散射簇的数目和初始簇中心的位置，然后以结合了多径功率加权的多径分量距离为准则进行多径簇聚类．仿真结果表明：与KPowerMeans算法相比，采用所提出的WKPowerMeans算法能得到更稳定、准确的聚类结果，而且具有较低的时间复杂度．

多径簇识别；KPowerMeans算法；信息熵；尖峰检测

在无线通信中，电磁波的传播可以用传播径近似表征．传播径可以通过一个多维参数集描述，该参数集一般包括能量、时延、到达角和离开角等多径特性．一般将具有相近参数的多径归为一个簇进行统计特性研究，一些主流的无线宽带信道模型(SCM/SCME/WINNER)都是基于多径散射簇进行建模的．对传播径进行簇识别的准确性有助于分析多径簇的生灭过程和多径分量的簇统计特性，进而影响信道建模的准确性．

多径簇识别算法是目前基于多径簇的信道建模和信道特性分析领域的研究热点．将模式识别中的聚类算法应用于无线信道自动簇识别研究的多径簇识别算法大致分为3类：基于层次的多径簇识别聚类算法[1]、基于划分的多径簇识别聚类算法[2]和基于密度的[3]多径簇识别聚类算法．

基于划分的聚类算法的代表是KMeans算法．文献[2]提出了一种基于KMeans算法的改进的簇识别算法KPowerMeans，此算法在计算相互邻近的多径的距离时考虑了多径功率的影响，并且引入了2个衡量聚类效果的参数来确定多径簇的数目．但该算法没有考虑多径属性的差异性对多径加权因子的影响，并且有严重依赖于对初始聚类中心的选择、容易陷入局部最优解等缺陷．针对这些不足，本文引入了小波变换和信息熵自适应加权技术以改进KPowerMeans聚类算法．

本文提出的改进KPowerMeans算法在进行多径聚类之前通过小波尖峰检测技术确定多径簇的数目及初始簇中心，有效克服了KPowerMeans算法对初始聚类中心的敏感性，然后根据多径的属性对于分类不同的贡献度，利用信息熵原理对多径分量距离进行特征加权以提高分类精度．由于引入了小波尖峰检测技术和自适应信息熵加权算法，笔者将此算法命名为WKPowerMeans(wavelet weighted KPowerMeans)算法．

本文详细介绍了所提出的改进算法的框架、流程及相关技术，并通过仿真给出了与文献[2]算法的性能比较．

1 KPowerMeans算法

KPowerMeans算法通过对可能范围内的多径簇的数目[Kmin，Kmax]进行多径聚类，引入了2个衡量聚类效果的参数CH(calinski-harabasz)和DB(daviesbouldin)，取最大的CH或DB指数所对应的K作为最优的的多径簇的数目[4]．KPowerMeans算法的具体流程如图1所示，步骤如下所述．

图1 KPowe rMeans算法流程Fig.1 Flow chart of KPowerMeans algorithm

步骤2 将不同多径分量分配给不同的簇，并保存索引值．

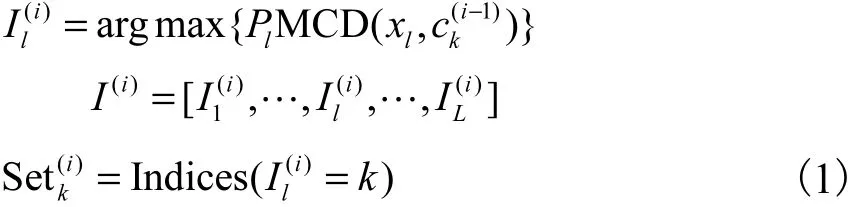
步骤3 重新计算K个簇中心的位置cK(0)，根据新分配的每一个簇内的多径信息，使得簇内多径的差异性之和D最小，即

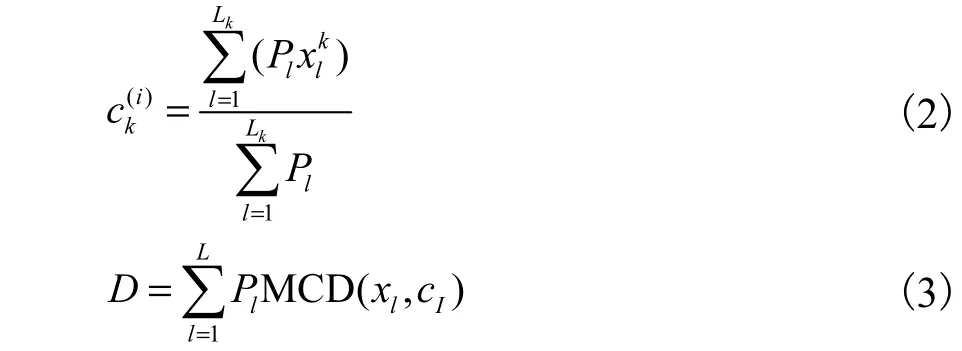
2 WKPowerMeans算法

本文提出的WKPowerMeans算法的基本流程和KPowerMeans算法有相同的框架，但在具体步骤中有所改进．流程如图2所示．

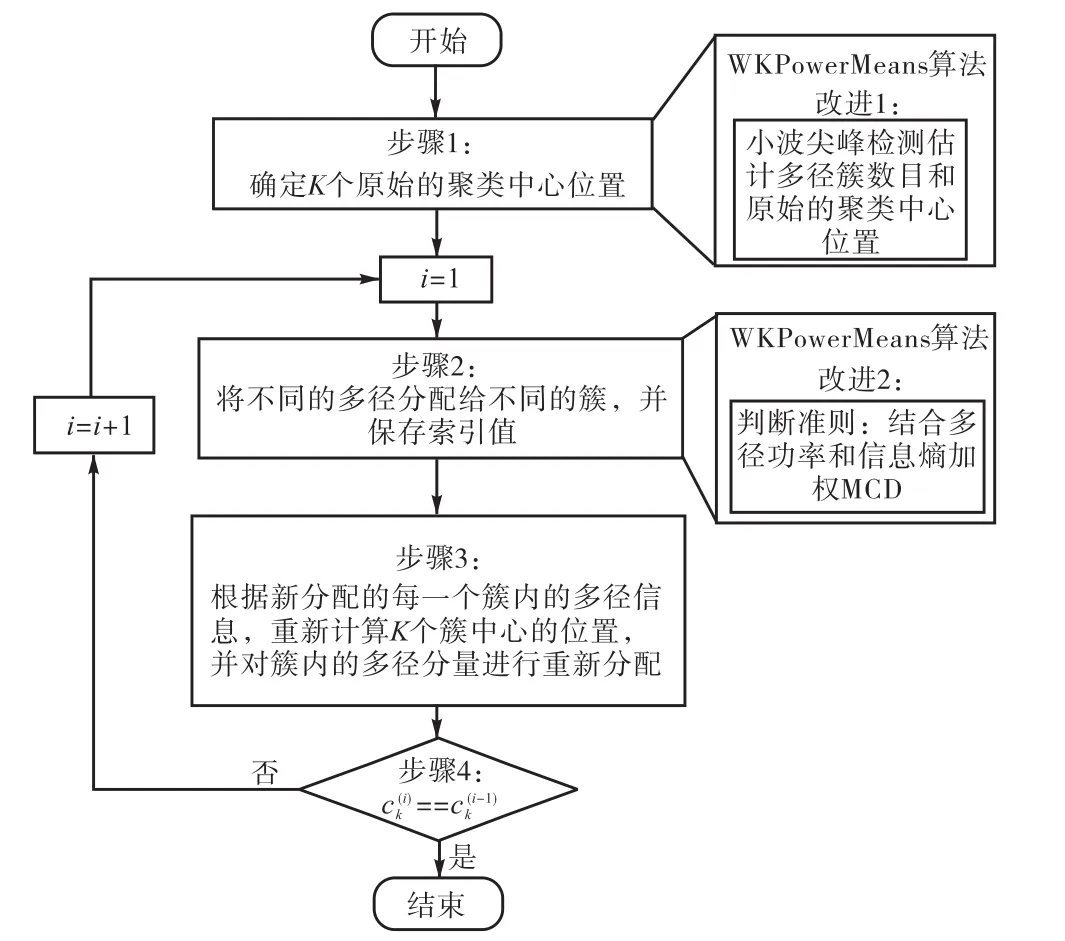
图2 WKPowerMeans算法流程Fig.2 Flow chart of WKPowerMeans algorithm

WKPowerMeans算法的改进点在于：在步骤1中，采用小波变换的尖峰检测技术代替随机选择，这种带监督的聚类算法能克服对初始聚类中心的敏感性，从而获得稳定的聚类效果；步骤2中，在考虑了多径功率影响的基础上，引入信息熵原理计算多径属性自适应加权的多径分量距离(MCD)．

2.1 小波尖峰检测技术

根据Saleh-Valenzuela信道模型的描述[5]，接收信号的多径分量以簇的形式到达，并且多径幅度大小呈双指数形式衰减．图3所示为Saleh-Valenzuela信道模型的功率时延谱(power delay profile，PDP)．

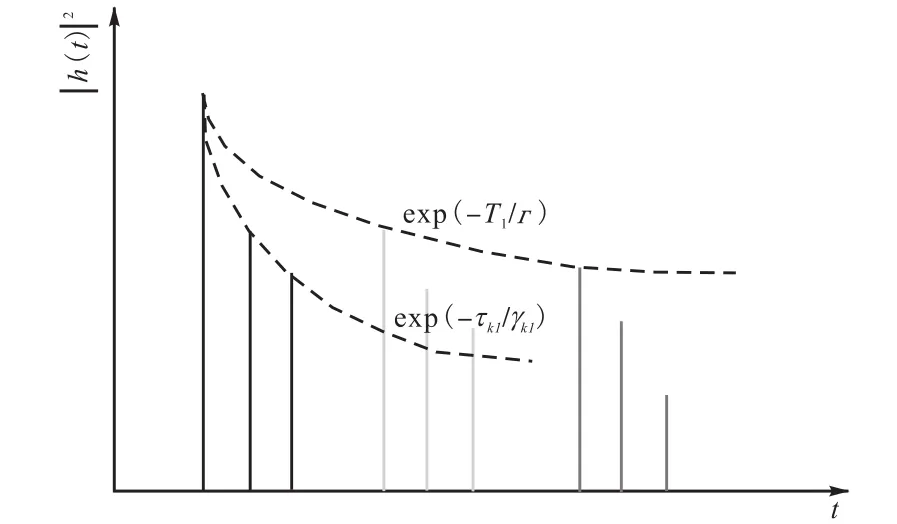
图3 SV模型功率时延谱Fig.3 PDP of SV model

这种多径成簇的现象导致功率时延谱有明显的尖峰，因而可采用小波变换来得到多径能量的跳变点的位置[6]．小波基函数一般可用尺度参数α和位移参数β来表示[7]．对信道冲击响应CIR进行小波变换，可得到

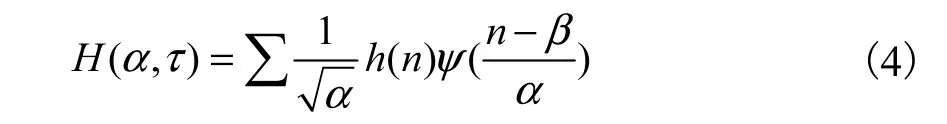
式中ψ(·)为母小波．本文选择Daubechies小波来进行多径能量的峰值检测，因为相比于其他小波，Daubechies小波的瞬时消失特性更适于用来检测信号的跳变点[8]．

2.2 多径分量距离

文献[9]用多径分量距离来衡量多径分量之间、簇心之间、多径分量和簇心之间的距离，即多径分量i与j之间的距离可表示为

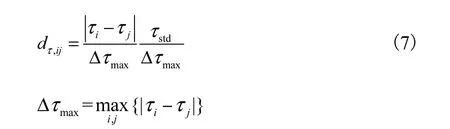
式中：wAOA、wAOD、wτ分别表示dAOA,ij、dAOD,ij、dτ,ij等不同属性参数所对应的权值；dAOA,ij和dAOD,ij分别表示到达角、离开角的角度距离MCD值；dτ,ij为多径时延的多径分量距离；stdτ为时延的标准差．

2.3 信息熵加权

由于不同的多径属性对MCD的影响权值随着不同的场景、频段而变化．借助信息论中的信息熵原理[10]，本文提出的改进算法根据各多径属性的变异程度，计算各多径属性对MCD的权重影响因子，为无序数据对象集聚类提供依据[11]．

(1) 假设有n条多径(即n个待聚类数据对象)，每一径数据对象具有m维属性．根据实时数据可构造一个n×m大小的属性值矩阵，即

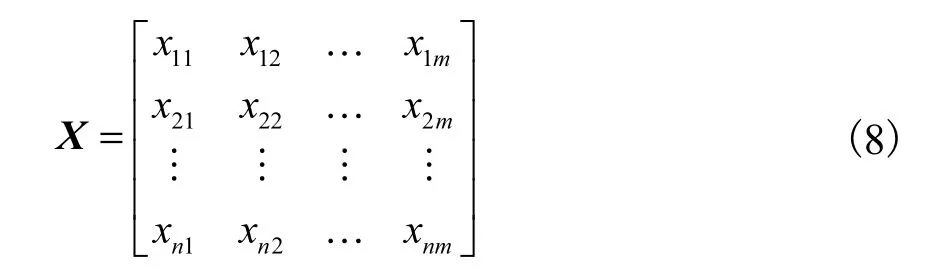
式中xij为第i条多径分量的第j维属性．

本文的算法中取m=3，分别对应多径的到达角AOA、离开角AOD和时延τ这三维信道的属性参数.

(2) 计算第j维属性对应的第i个数据对象的属性值比重．由于角度属性的范围是(-π，π]，为保证计算的影响因子为正数，将角度数据集进行线性映射变换，即将数据压缩到区间[0，1]上，再计算其属性比重，即

式中：Mij为xij属性值所占比重；j∈[1，m]且j∈Z；i∈[1，n]且i∈Z．

(3) 计算第j维属性的熵值．

式中Hj为属性熵值，当Mij=0时，令Hj=0．(4) 计算第j维属性的差异性系数．

式中qj为差异性系数．qj越小，该属性的聚类作用就越小．

(5)计算第j维属性的权值比重．

式中0≤wj≤1．∑wj=1，j∈[1，m]且j∈Z．将得到的各属性的权值wj带入式(5)，用于计算多径分量的MCD．而KPowerMeans聚类算法在进行多径簇的识别的过程中，将属性参数的权值wj分别设置为经验值[12]：wAOA=0.5，wAOD=0.5，wτ=5，不具有普适性．

3 实例分析

本文以3,GPP的SCM信道模型[13]为例，实际测量中可通过SAGE算法进行信道参数的提取，得到每一条多径分量的到达角AOA、离开角AOD和时延信息．本文使用多径分量的信道参数由3,GPP的SCM信道模型自动生成，没有涉及信道参数的提取过程．根据SCM模型的定义，所有的角度信息均为二维的方位角(不考虑俯仰角)．然后利用本文提出的WKPowerMeans算法对多径分量进行聚类分析，并与文献[2]提出的KPowerMeans算法的聚类结果进行分析比较．

SCM模型设置为收发端均采用8元均匀线性天线阵，天线间隔为0.5,λ，场景设置为城市微小区(urban micro)．SCM信道模型中的多径时延通过指数分布确定(其中均方根时延扩展为高斯分布的随机变量)，而每一路径的到达角与离开角由均匀分布的簇到达角和服从拉式分布的簇内偏移角度随机变量叠加构成．

图4是从SCM信道冲击响应提取的多径分量的到达角AOA、离开角AOD和时延的分布．图中每一个点表示每一条多径分量，每一个点的灰度值表示此多径分量的功率．图中，通过SCM信道模型得到的多径分量共有120条，可分辨出6组多径散射簇．

图5为对信道冲击响应CIR进行3层小波分解后的一级细节信号的小波系数．图中的能量峰值即为多径能量的跳变点的位置，即每一多径散射簇中的能量主径．能量峰值的数目即检测到的多径散射簇的数目，能量峰值所对应的x轴的数值即是簇的中心位置所对应的多径分量的编号．可见，采用尖峰检测技术不仅确定了多径散射簇的数目K=6，同时还得到了聚类算法的初始簇中心的位置x=(4，25，44， 64，81，102)．

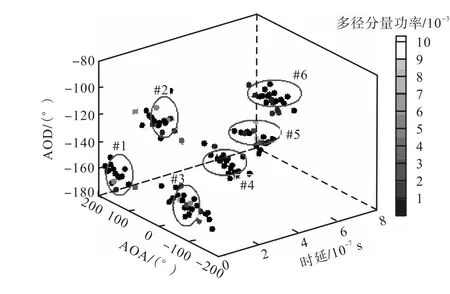
图4 信道冲击响应的一次实现Fig.4 Snapshot of channel impulse response

图5 小波变换的能量跳变点Fig.5 Energy peak using wavelet transformation

图6 为分别采用KPowerMeans算法和WKPower Means算法对图4中SCM模型得到的多径分量进行自动簇识别的结果对比．不同形状的点标识用于区分多径分量所属的不同的多径散射簇．图6(a)和图6(b)显示的KPowerMeans算法聚类的结果与图4所示有偏差，原本不属于同一散射簇的多径分量被错误地归为一类．通过图6(a)和图6(b)对比还显示，由于初始簇中心位置的随机性导致每一次聚类的结果不尽相同．图6(c)显示的结果则为通过本文提出的WKPowerMeans算法得到的多径散射簇的分布图．多次仿真的结果显示，由于采用小波变换的尖峰检测技术，唯一地确定了初始簇中心位置，从而保证了聚类结果的唯一性．

3.1 聚类精确度分析

表1为2种算法对SCM信道模型的多径数据集的聚类精确度比较，改进后的WKPowerMeans算法的聚类精确度不仅提高到98.33%，并且由于所有的多径簇都以每个多径簇中的最强径为中心，不会出现文献[2] WKPowerMeans算法的聚类结果不稳定的情况．

表1 两种算法的聚类比较Tab.1 Comparison of two kinds of clustering algorithm

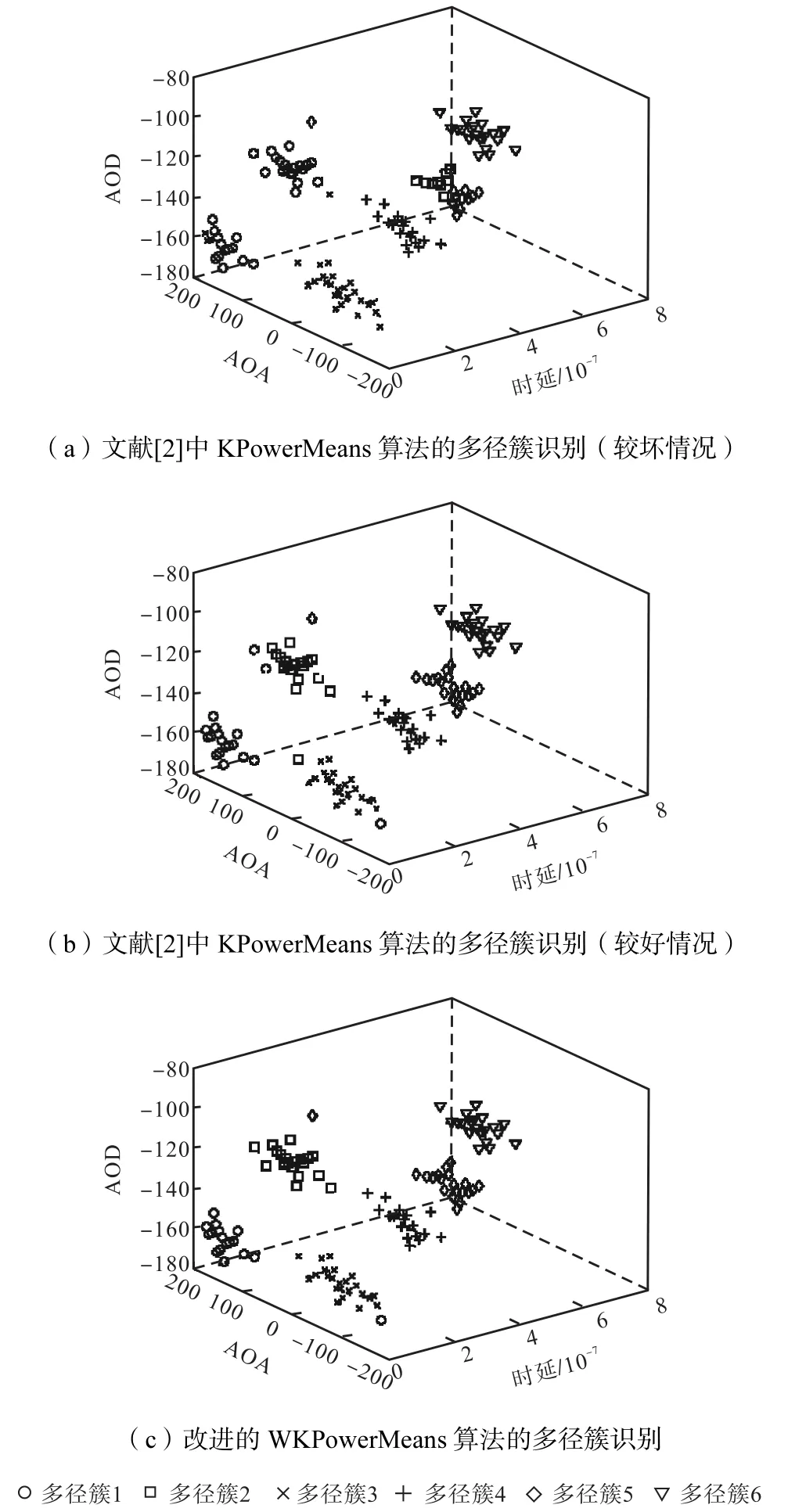
图6 自动多径簇识别结果Fig.6 Results of automatic clustering identifitio n

3.2 时间复杂度分析

KPowerMeans算法由于需要先通过遍历可能范围内的多径簇的数目[Kmin，Kmax]进行多径聚类，取最大的CH或DB指数所对应的K作为最优的多径簇的数目．其算法的时间复杂度为O(Ltkn)，其中n为待聚类数据对象数，k为聚类的类数，t为聚类稳定的迭代次数，L为可能的多径簇数目的范围(L=Kmax-Kmin+1)．

本文提出的WKPowerMeans算法由于利用信道冲击响应的特性直接确定多径簇的数目，其时间复杂度为O(tkn)，是KPowerMeans算法的1/L．

4 结 语

针对KPowerMeans算法确定类别数的过程复杂和由于随机簇中心导致聚类结果不稳定的问题，本文提出的WKPowerMeans算法采用小波尖峰检测技术进行初始聚类中心点选择和多径簇数目的估计，并根据待聚类的数据集进行自适应的属性加权，强化了不同属性对多径分量距离(MCD)的聚类影响．仿真结果表明：相比于KPowerMeans算法，本文提出的WKPowerMeans算法提高了多径簇识别的稳定性和准确度，降低了时间复杂度．

［1］ Czink N，Mecklenbrauker C，Del G G. A novel automatic cluster tracking algorithm [C]// IEEE 17th International Symposium on Personal，Indoor and Mobile Radio Communication. Helsinki，Finland，2006：1-5.

［2］ Czink N，Cera P，Salo J，et al. A Framework for automatic clustering of parametric MIMO channel data including path powers [C] // IEEE 64th Vehicular Technology Conference 2006. Montreal，Canada，2006：1-5.

［3］ Bernado L，Roma A，Czink N，et al. Cluster-based scatterer identification and characterization in vehicularchannels [C] // Wireless Conference 2011 Sustainable Wireless Technologies(European Wireless)，11th European. Vienna，Austria，2011：1-6.

［4］ Li Tian，Yin Xuefeng. Multi-path grouping using a novel clustering algorithm for stochastic channel modeling[C]// 2010 6th International Conference on Wireless Communications Networking and Mobile Computing(WiCOM). Chengdu，China，2010：1-4.

［5］ Saleh A A M，Valenzuela R. A statistical model for indoor multipath propagation [J]. IEEE Journal on Selected Areas in Communications，1987(5)：128-137.

［6］ Liang J Y，Zhao X W，Li D Y，et al. Determining the number of clusters using information entropy for mixed data [J]. Pattern Recognition，2011，45：2251-2265.

［7］ Du Pan，Kibbe W A，Lin S M. Improved peak detection in mass spectrum by incorporating continuous wavelet transform-based pattern matching[J]. Bioinformatics，2006，22(17)：2059-2065.

［8］ Fard P J M，Moradi M H，Tajvidi M R. A Novel approach in R peak detection using hybrid complex wavelet(HCW)[J]. International Journal of Cardiology， 2008，124(2)：250-253.

［9］ Czink N. Improving clustering performance using multipath component distance[J]. Electronics Letters，2006，42(1)：33-35

［10］ Zhang Zhen，Yeung R W. On characterization of entropy function via information inequalities [J]. IEEE Transactions on Information Theory，1998，44(4)：1440-1452.

［11］ Jing Liping，Ng M K，Huang J Z. An entropy weighting k-means algorithm for subspace clustering of highdimensional sparse data [J]. IEEE Transactions on Knowledge and Data Engineering，2007，19(8)：1026-1041.

［12］ Huang J Z，Ng M K，Rong H Q，et al. Automated variable weighting in k-means type clustering [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，2005，27(5)：657-668.

［13］ Salo J，Galdo D G，Salmi P，et al. MATLAB implementation of the 3,GPP spatial channel model(3,GPP TR 25.996)[EB/OL]. http： //www.ist-winner.org/3gpp_scm. html，2012-07-06.

(责任编辑：金顺爱)

WKPowerMeans Approach to Multipath Cluster Identification

Yang Jinsheng，Wu Xuzhao
(School of Electronic Information Engineering，Tianjin University，Tianjin 300072，China)

In order to solve the problems of KPowerMeans multipath cluster recognition algorithm，which has a complex process of multipath scattering cluster estimation and whose clustering result is highly dependent on the random initial cluster cancroids. An improved algorithm，named WKPowerMeans，is proposed. The peak detection and information entropy methods are combined to develop the framework of automatic cluster identification. The improved algorithm not only acquires the number of cluster and initial centroids by using the wavelet transformation，but also adaptively obtains the different weights of the attributes of the multipath component. Simulation results indicate that the proposed WKPowerMeans clustering method can produce more robust and more accurate solutions than KPowerMeans method；furthermore it has lower time complexity.

multipath cluster identification；KPowerMeans algorithm；information entropy；peak detection

TN929

A

0493-2137(2014)03-0237-06

10.11784/tdxbz201209015

2012-09-06；

2012-12-14.

国家科技重大专项资助项目(2010ZX03005-001).

杨晋生（1965— ），男，博士，副教授．

杨晋生，jsyang@tju.edu.cn.