紊动对黏性泥沙絮凝沉降影响的实验研究

乔光全，张金凤，张庆河，肖金龙，夏 波

(1.天津大学水利工程仿真与安全国家重点实验室，天津 300072；2.国家海洋局南海工程勘察中心，广州510300；3.湖南省水沙科学与水灾害防治重点实验室，长沙 410004)

紊动对黏性泥沙絮凝沉降影响的实验研究

乔光全1,2，张金凤1，张庆河1，肖金龙1，夏 波3

(1.天津大学水利工程仿真与安全国家重点实验室，天津 300072；2.国家海洋局南海工程勘察中心，广州510300；3.湖南省水沙科学与水灾害防治重点实验室，长沙 410004)

在圆柱形沉降筒中利用多层格栅产生近似各向同性紊流场，研究盐水和淡水中紊动对黏性泥沙絮凝沉降的影响，分析絮团粒径、体积含量和泥沙浓度变化．研究结果表明：在相同剪切率条件下，和在淡水中相比，盐水中黏性泥沙絮凝时间缩短，絮团粒径增加，然而盐度对絮团体积含量影响并不明显；最大絮团粒径随着紊动剪切率的增加先增大后减少，最大絮团粒径对应的紊动剪切率在盐水中为 20.8,s-1，淡水中为 15.6,s-1；随着紊动剪切率的增加，水体中泥沙平衡浓度增大，达到平衡所需要的时间缩短．

振动格栅；紊动剪切；盐度；黏性泥沙；絮凝沉降；泥沙浓度

黏性泥沙的絮凝沉降对细颗粒泥沙构成的淤泥质河口海岸地形及环境演化有重要影响，而絮凝沉降本身又受到颗粒大小、泥沙浓度、水体盐度、水体紊动以及有机物等多种因素的影响．对于处于不断运动状态的河口海岸水体而言，水体紊动是影响泥沙絮凝沉降的重要影响因素．

不少学者利用现场观测、室内实验和数值模拟手段研究了紊动对黏性泥沙絮凝的影响规律. Winterwerp等[1]对 Scheldt河口黏性泥沙絮团进行现场测量，提出了包含水体紊动参数的黏性泥沙沉速公式并应用于计算模型中．唐建华等[2]、Liu等[3]和杨扬等[4]分别通过室内实验和现场观测等方法研究了水体紊动、盐度和腐殖酸含量等因素对长江口细颗粒泥沙絮凝沉降的影响，认为水流动力条件会直接导致絮凝体的破碎，而盐度和腐殖酸的增加则促进絮凝体的形成．张金凤等[5]建立均匀各向同性紊流中黏性泥沙絮凝沉降的格子玻耳兹曼数学模型，模拟了不同紊动剪切率对黏性泥沙絮凝沉降的过程，认为低强度紊动水体促进絮凝，而高强度紊动抑制絮凝．Gratiot等[6]利用单层格栅振动实验研究了紊动和有机物对河口泥沙絮凝特性的影响，认为紊动剪切率在 3～19,s-1范围内时，水体紊动促进黏性泥沙的絮凝．吴荣荣等[7]通过环形水槽研究了钱塘江口泥沙的动水絮凝沉降现象，认为流速是影响泥沙动水沉降的主要因素，钱塘江河口细颗粒泥沙的絮凝临界流速为 60,cm/s．Mietta等[8]用烧杯和沉降筒两种尺度的实验容器研究了紊动引起的黏性泥沙絮凝特性，认为紊动水体中絮团粒径受水体环境(包括pH值、盐度和有机物含量等)影响，紊动剪切率为20,s-1左右时，絮团粒径最大．Cuthbertson等[9]在多层格栅振动产生的均匀紊流场中研究了黏性泥沙以及混合沙的絮凝沉降特点，认为高紊动水体中，泥沙絮凝时间与絮团粒径及泥沙初始浓度有关；而低紊动水体中，其关系不明显.

上述研究结果从多种角度揭示了紊动对黏性泥沙絮凝的影响规律，然而，现有的振荡格栅实验研究并未考虑海水和淡水不同环境中紊动对絮凝过程的影响．为此，笔者在沉降筒中采用多层振动格栅产生均匀紊流场，研究不同紊动条件下盐水和淡水中黏性泥沙的絮凝沉降过程，分析黏性泥沙絮凝稳定时间、絮团体积含量、絮团粒径以及实验过程中泥沙浓度的变化，比较盐水和淡水中紊动对黏性泥沙絮凝沉降的影响规律．

1 实验设备与方法

1.1 实验设备和材料

实验所用沉降筒系统主要由沉降筒、格栅和电机3个部分组成，其结构及尺寸如图1所示．沉降筒材料为有机玻璃，高100,cm，外直径 30.00,cm，筒壁厚1.00,cm. 为在沉降筒中产生较大范围的均匀紊流[9-10]，共设 3层振动格栅，相邻格栅间距 H=30,cm，对每个格栅，相邻格栅孔的距离M=5.50,cm，格栅条厚度和宽度都为1.00,cm，格栅空隙率(格栅开口面积与总面积之比)为 0.67，能产生较稳定的紊流场[9]．底层格栅平衡位置距离沉降筒底部15,cm，大于2.5,M，格栅边缘和壁面的距离为0.50,cm，能有效避免二次回流的影响[11]，格栅之间通过连杆相连，格栅上部和电机相连．电机转动速度为 0～600,r/min，对应格栅的振动频率 f=0～10,Hz，冲程为 S=1～10,cm，皆无级可调．实验中电机带动格栅做上下振动，通过调整电机转速产生不同紊动强度的近似各向同性均匀紊流．

图1 沉降筒及振动格栅示意(单位：cm)Fig.1 Schematic diagrams of settling column and oscillating grid(unit：cm)

在下两层格栅对应的沉降筒外壁上设置 5个取样口(见图 1)．通过取样口对泥沙粒度分布和絮团含量进行测量．通过测量泥沙样品的浊度，然后根据浊度和浓度的关系反算得到泥沙浓度[12]．本实验采用美国哈希 2100P型便携式浊度仪进行浊度测量，浊度仪测量范围为 0～1,000,NTU，分辨率为测量精度的 1.0%，连续读数模式的测量反应时间为 6,s，每组测量3次取平均值作为实验结果．

泥沙粒度分布采用马尔文MasterSize 2000激光粒度仪进行测量和分析，它由激光器、滤波扩束系统、样品窗、光电探测器和计算机处理系统组成，测量范围为 0.02～2,000,µm，测量准确度为±1.0%．测量时将一定量待测泥沙样品加入到蒸馏水中，在螺旋桨的作用下充分分散，对样品颗粒进行粒度分析，当需要测量泥沙单颗粒粒径分布时要开启超声波作用，以将泥沙悬浮液中的絮团充分打散．每组实验测量 3次取平均值作为最终结果．

实验用沙为煅烧高岭土，其中d50=3.93,µm，d10= 1.26,µm，d90=10.23,µm，粒径分布较集中且都属于黏性泥沙范畴(见图2)．实验用盐水采用人工配制的Sunbow海水[4]，组成物成分比例见表1，盐度为0.5%．

1.2 实验原理和参数率定

已有研究表明，振动格栅能够在沉降筒中产生稳定的近似各向同性均匀紊流[11]．Camp和 Stein[13]提出紊动剪切率和耗散率之间的关系为

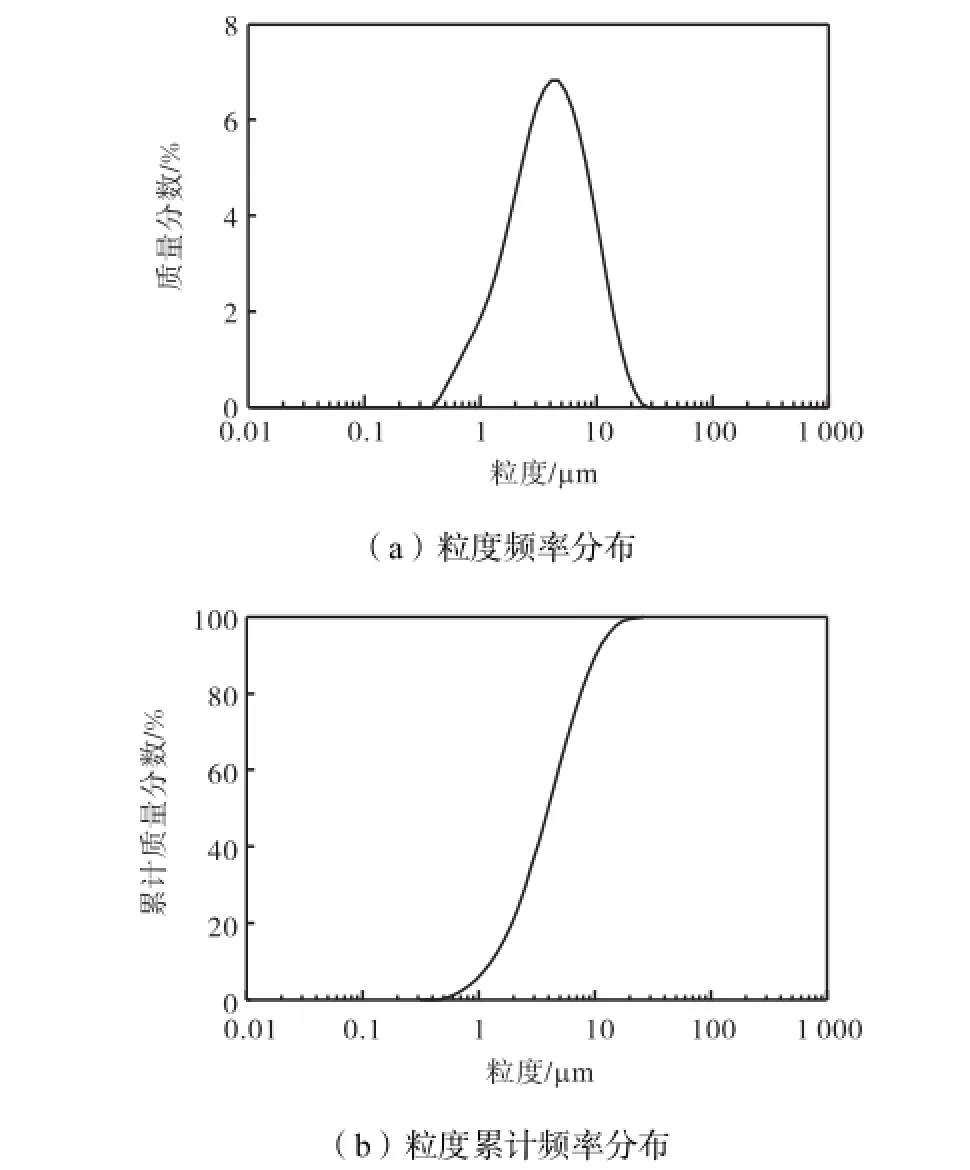
图2 泥沙粒度频率和累计频率分布Fig.2 Distributions of sediment size and its cumulative percentage

表1 人工配制海水成分Tab.1 Composition of artificial sea water

式中：G为紊动剪切率；ε为紊动能量耗散率；ν为流体运动黏滞系数．其中，紊动能量耗散率ε和紊动能量积分尺度有关[9]，其表达式为

式中：A为接近于 1的常数；u'为紊动场的均方根流速(root-mean-square velocity)；l为紊动空间积分尺度．Shy等[10]认为当紊流场中只有某点(而不是场)速度的时间序列时，紊动空间积分尺度l可以通过时间积分尺度lt求得，即

式中：lt为紊动时间尺度；t0为Rt(r，t)首次为0时的t值；Rt(r, t)为时间相关函数，其表达式为

式中 uτ、uτ+t分别为场中某点间隔时间 t的脉动速度．由于本实验采用 ADV测量单点的速度时间序列，因此紊动空间积分尺度由式(3)～(5)求得，实验时脉动速度由ADV测得．

均方根速度与格栅尺寸、格栅振幅、振动频率及测量点有关，在多层格栅实验中均方根流速的求解可以看成是两层格栅作用效果的叠加[9]．定义两层格栅中间位置处为z=0，u'(z)的表达式为

通过以上分析可知，为得到紊动剪切率 G，需要通过实验对速度系数 B和空间(时间)相关尺度 l(lt)进行率定．为了得到速度系数 B，利用 ADV测量不同格栅冲程、不同振动频率产生的紊动场中某点的速度历时，计算出均方根速度，绘制出其和 M0.5S1.5fz-1的关系，如图3所示．

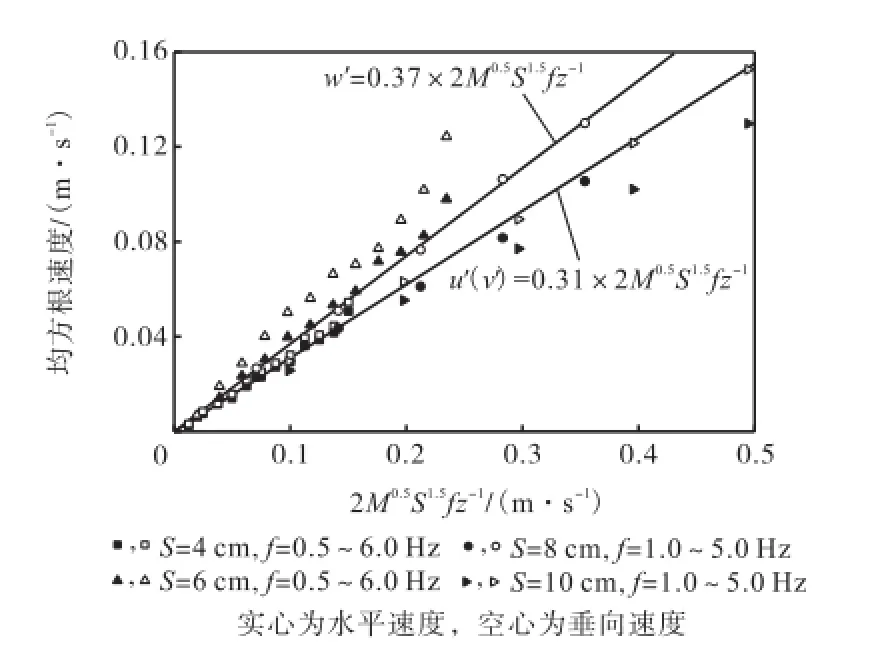
图3 均方根速度和M0.5S1.5fz-1关系Fig.3 Relationship between root-mean-square velocity and M0.5S1.5fz-1

当冲程 S＜10,cm时，二者呈现很好的正比例关系．对于本文的振动格栅装置，拟合得到水平向速度系数为 0.31，垂向速度系数为 0.37．上述结果与其他学者得到的结果较为接近，如 Shy等[10]认为 B= 0.445；Medina等[14]根据实验得到B=0.30．根据所得数据和式(5)绘制出紊动场中的时间相关函数曲线，如图4所示(冲程S=4,cm)．将时间相关曲线进行积分计算并带入式(3)，得到水平和垂向空间积分尺度为 1.11,cm和1.49,cm，与 Cuthbertson等[9]在双层振荡格栅紊动场得到的结论(S/H＜0.15时，l=1.35,cm)接近．由于本实验主要研究泥沙在垂向的运动，且两个方向上的积分尺度相差不大，因此紊动空间积分尺度采用1.49,cm．

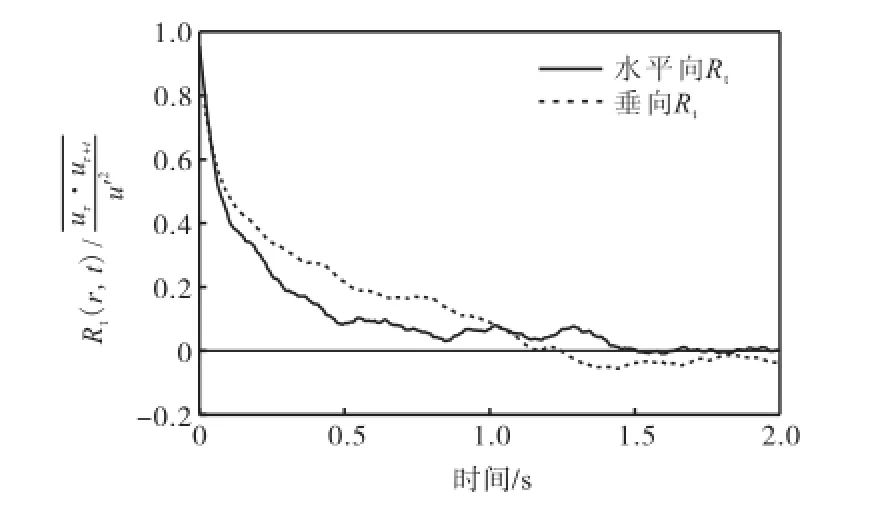
图4 时间相关系数曲线Fig.4 Time correlation coefficient

将上述系数依次带入式(6)、式(2)和式(1)中，得到冲程S为4,cm时该实验装置产生的紊动剪切率G和格栅振动频率f之间的关系为

1.3 实验过程

考虑到浊度仪等实验仪器的测量范围，实验中泥沙质量浓度选 0.1,g/L，水体盐度取 0.5%[15]，紊动剪切率 G为 0、5、10、20、30、40、60、80 s-1，同时每组实验在淡水(盐度为0)中重复1次，共计16组实验．

实验之前先安装好测量仪器并向沉降筒中注入约40,L水备用．首先称量盐度为0.5%盐水的用盐量和质量浓度为 0.1,g/L的实验用沙，分别置于 5,L水中充分搅拌使其均匀分布；然后把盐水和泥沙悬浮液分别注入沉降筒中，整个过程一直保持格栅10,Hz振动，以使泥沙在沉降筒中混合均匀且尽量减少絮凝的发生[8]；待泥沙混合均匀后，调整电机转速，将格栅振动频率调至所需频率并开始计时，用ADV不间断地测量上两层格栅中间的流速，采样频率 200,Hz．在下两层格栅中间取样口取沙洋，使用浊度仪测量样品泥沙浓度，测量时间间隔为 2～20,min，同时每隔20,min用激光粒度仪测量样品泥沙粒径分布，这样流速测量和取样测量两者互不干扰．实验水温也通过ADV测量，每次实验前后温差小于0.5,℃，全部组次的实验水温在(23.5±1.5),℃范围内．由于温差较小，本文暂不考虑温度对泥沙絮凝的影响．

2 实验结果与讨论

2.1 絮凝结果分析

图 5为实验过程中泥沙悬浮液典型的粒度体积含量分布，图中左侧峰值对应泥沙单颗粒粒度分布，右侧峰值对应絮团粒度分布．若以 cp表示单组分泥沙颗粒的含量，cf和df分别表示单组分泥沙絮团含量及对应的粒度，则图中左侧峰值下面以横线填充的面积可以认为是单颗粒泥沙体积含量，即单颗粒泥沙体积与泥沙总体积之比，右侧峰值下面斜线填充的面积为絮团体积含量，即泥沙絮团体积与泥沙总体积之比．Cp与 Cf的和为100%，絮团平均粒径

图 6给出了实验过程中絮团粒径和絮团体积含量(絮团体积占泥沙总体积的百分比)历时变化曲线，实线和虚线分别表示盐水(s=0.5%)和淡水的实验结果，图中只给出了G为5、20、60、80 s-1的情形．从图6中可以看出，黏性泥沙在盐水中的絮凝沉降过程表现为：高紊动水体中，由于颗粒碰撞频率增加促进絮团形成，絮团粒径和体积含量先迅速增大，之后水体紊动使得大絮团破裂形成较小絮团，絮团粒径逐渐减小至趋于平衡，而絮团含量则从开始缓慢增大至趋于平衡；低紊动水体中絮团粒径和含量均是逐渐增大达到平衡后基本保持不变．淡水中，絮团粒径和体积含量随时间的变化规律和盐水中低紊动剪切率的表现基本相同，只是达到稳定絮凝的时间较长．在不同的紊动剪切率(G为 0、5、10、20、30、40、60、80 s-1)条件下，以絮团体积含量达到稳定作为絮凝稳定的时间，盐水和淡水絮凝稳定时间分别为 170、150、150、130、90、70、50、30 min和 210、210、190、150、130、110、90、70 min．

图 7给出了絮凝平衡时絮团粒径和紊动剪切率的关系，并给出了实验结果的拟合曲线．结合图6(b)可以看出：紊动剪切率的增加虽然会使黏性泥沙絮团含量一直增大，但其对絮团粒径的影响却表现为先使其增大后减小．盐水中，絮团粒径最大值出现在紊动剪切率 G=20.8,s-1时，与已有的实验结果[16]和数值模拟结果[5]一致．如张金凤等[5]对紊动引起的絮凝进行数值模拟，通过剪切应力τ求得剪切率G=τ/µ，认为絮凝剪切率的转折点是 200,s-1；如果剪切率按照式(1)计算，相当于数值模拟得到的最佳絮凝对应的紊动剪切率为17.6,s-1，与本文实验结果接近．

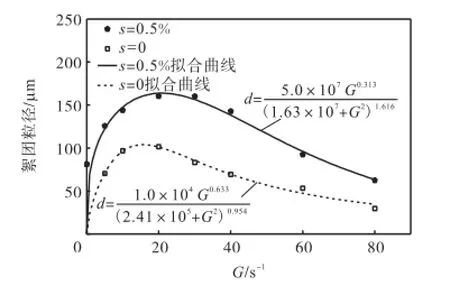
图7 絮凝平衡时絮团粒径随紊动剪切率的变化Fig.7 Relationship between the floc size and turbulence shear rate at the steady state

此外，淡水和盐水中，最有利絮凝的紊动剪切率不同，盐水中为20.8,s-1，而在淡水中絮团粒径最大值则出现于紊动剪切率15.6,s-1；紊动剪切率相同时，盐水中絮团粒径明显大于淡水中的粒径，前者是后者的1.48～2.10倍，说明水体盐度对泥沙絮凝有促进作用.

2.2 泥沙浓度结果分析

盐水中不同紊动条件下，泥沙相对体积浓度变化如图8所示，图中只给出了G为0、20、40、80 s-1的情形，纵坐标表示泥沙相对浓度，C和C0分别是时刻t和初始时刻的泥沙浓度．

本文采用二级动力学沉降模式[15]分析实验数据，其表达式为

式中 a、b为无量纲拟合参数．当絮凝沉降达到平衡时，泥沙相对浓度将减小 1/b，达到 1-1/b，b越大，稳定浓度越大；浓度变化量达到其最大变化量一半(0.5/b)时，需要的时间 t0.5=a/b，浓度平均变化率为1/2,a，即 a越大，浓度变化越慢，达到稳定浓度的时间越长．图 8中，线表示采用式(8)对不同紊动剪切率实验结果的拟合．从图中可以看出：静水中泥沙相对浓度呈线性递减，这主要是由泥沙颗粒不断沉降导致的；而在紊动水体中，由于泥沙颗粒沉降，相对浓度先有所减少，但由于紊动水体具有一定的挟沙能力，泥沙趋于沉降与悬浮的平衡，相对浓度又逐渐趋于平衡状态．紊动剪切强度越大，水体挟沙能力越大，趋于平衡的相对浓度也越大．

图8 泥沙浓度历时曲线Fig.8 Time series of sediment concentration

图9给出了盐水和淡水环境下，拟合曲线中参数a和 b随紊动剪切率的变化，从图中可以看出，相同紊动剪切率条件下，盐度增大，b增大，说明泥沙的稳定浓度增大；a减小，说明浓度达到稳定的时间变短．淡水条件下泥沙絮凝慢，泥沙浓度变化也慢，泥沙稳定浓度小．

图9 系数a、b随紊动剪切率G的变化Fig.9 Relationship between parameters a，b and turbulence shear rate G

3 结 语

本文利用多层振动格栅产生近似均匀紊流场，取样测量了中值粒径 3.93,µm 的黏性泥沙在紊动流场中的絮凝沉降特性，包括絮团体积含量、絮团粒径和泥沙浓度等，分析了紊动剪切率和盐度对絮团特性及泥沙浓度的影响，主要结论如下：

(1) 针对本实验的格栅参数，紊动剪切率和格栅振动频率的关系为G=7.30,f1.5；

(2) 絮凝平衡时，絮团粒径随着紊动强度的增强呈先增加后减少的趋势，同时紊动对黏性泥沙的絮凝沉降作用受到盐度的影响；

(3) 相同紊动剪切率下，盐水中(s=0.5%)黏性泥沙的絮凝特性和淡水中的相比，絮团体积含量略有增加，絮凝时间明显缩短，絮团粒径明显增大；

(4) 相同盐度条件下，紊动增强使絮团含量增加，絮凝时间缩短，絮团粒径随紊动强度增大先增大后减小，最大絮团粒径对应的紊动剪切率在盐水和淡水中分别为20.8,s-1和15.6,s-1；

(5) 相同紊动剪切条件下，盐度增大了泥沙的稳定浓度；同时在相同盐度条件下，随着紊动剪切率增加，泥沙稳定浓度也随之增大，稳定时间变短．

［1］ Winterwerp J C，Manning A J，Martens C，et al. A heuristic formula for turbulence-induced flocculation of cohesive sediment[J]. Estuarine，Coastal and Shelf Science，2006，68(1/2)：195-207.

［2］ 唐建华，何 青，王元叶，等. 长江口浑浊带絮凝体特性[J]. 泥沙研究，2008(2)：27-33.

Tang Jianhua，He Qing，Wang Yuanye，et al. Study on in-situ flocs size in turbidity maximum of the Changjiang Estuary[J]. Journal of Sediment Research，2008(2)：27-33(in Chinese).

［3］ Liu Q Z，Li J F，Xu C H，et al. Flocculation process of fine-grained sediments by the combining effect of salinity and humus in the Changjiang Estuary in China[J]. Acta Oceanologica Sinica，2007，26(1)：140-147．

［4］ 杨 扬，庞重光，金 鹰，等. 长江口北槽黏性细颗粒泥沙特性的试验研究[J]. 海洋科学，2010，34(1)：18-24.

Yang Yang，Pang Chongguang，Jin Ying，et al. Experimental study on characteristics of cohesive sediment in North Passage of the Yangtze River (Changjiang)estuary[J]. Marine Sciences，2010，34(1)：18-24(in Chinese).

［5］ 张金凤，张庆河，乔光全. 水体紊动对黏性泥沙絮凝影响研究[J]. 水利学报，2013，44(1)：67-72，82.

Zhang Jinfeng，Zhang Qinghe，Qiao Guangquan. The effects of turbulence on flocculation of cohesive sediments[J]. Journal of Hydraulic Engineering，2013，44(1)：67-72，82(in Chinese).

［6］ Gratiot N，Manning A J. An experimental investigation of floc characteristics in a diffusive turbulent flow[J]. Journal of Coastal Research，2004，SI 41：105-113.

［7］ 吴荣荣，李九发，刘启贞，等. 钱塘江河口细颗粒泥沙絮凝沉降特性研究[J]. 海洋湖沼通报，2007(3)：29-34.

Wu Rongrong，Li Jiufa，Liu Qizhen，et al. Study on flocculation and settling characteristics of cohesive fine grain sediment in the Qiantang Estuary[J]. Transactions of Oceanology and Limnology，2007(3)：29-34(in Chinese).

［8］ Mietta F，Chassagne C，Manning A J，et al. Influence of shear rate，organic matter content，pH and salinity on mud flocculation [J]. Ocean Dynamics，2009，59：751-763.

［9］ Cuthbertson A J S，Dong P，Davies P A. Nonequilibrium flocculation characteristics of fine-grained sediments in grid-generated turbulent flow [J]. Coastal Engineering，2010，57：447-460.

［10］ Shy S S，Tang C Y，Fann S Y. A nearly isotropic turbulence generated by a pair of vibrating grids [J]. Experimental Thermal and Fluid Science，1997，14(3)：251-262.

［11］ 闫 静，唐洪武，程年生，等. 振动格栅紊流及其应用综述[J]. 水利学报，2005，36(12)：1503-1509.

Yan Jing，Tang Hongwu，Cheng Niansheng，et al. Review on study of vibrating grid turbulence and its application [J]. Journal of Hydraulic Engineering，2005，36(12)：1503-1509(in Chinese).

［12］ 彭永勤，李克锋，曹 薇. 利用浑浊度推算含沙量方法的限制性与适应性研究[J]. 四川环境，2009，28(1)：20-23.

Peng Yongqin，Li Kefeng，Cao Wei. The restriction and applicability for the method of using turbidity to deduce sand content [J]. Sichuan Environment，2009，28(1)：20-23(in Chinese).

［13］ Camp T R，Stein P C. Velocity gradients and internal work in fluid motion [J]. Journal of the Boston Society of Civil Engineers，1943，85：219-237.

［14］ Medina P，Sánchez M A，Redondo J M. Grid stirred turbulence：Applications to the initiation of sediment motion and lift-off studies[J]. Physics and Chemistry of the Earth，2001，26(4)：299-304.

［15］ 关许为，陈英祖. 长江口泥沙絮凝静水沉降动力学模式的试验研究[J]. 海洋工程，1995，13(1)：46-50.

Guan Xuwei，Chen Yingzu. Experimental study on dynamic formula of sand coagulation sinking in stationary water in Changjiang Estuary [J]. The Ocean Engineering，1995，13(1)：46-50(in Chinese).

［16］ Mietta F，Chassagne C，Winterwerp J C. Shear-induced flocculation of a suspension of kaolinite as function of pH and salt concentration [J]. Journal of Colloid and Interface Science，2009，336(1)：134-141.

(责任编辑：赵艳静)

Experimental Investigation of the Influence of Turbulence on the Flocculation and Settling of Cohesive Sediment

Qiao Guangquan1,2，Zhang Jinfeng1，Zhang Qinghe1，Xiao Jinlong1，Xia Bo3
(1. State Key Laboratory of Hydraulic Engineering Simulation and Safety，Tianjin University，Tianjin 300072，China；2. South China Sea Marine Engineering Surveying Center，State Oceanic Administration，Guangzhou 510300，China；3. Hunan Province Key Laboratory of Water，Sediment Sciences and Flood Hazard Prevention，Changsha 410004，China)

An array of oscillating grids was applied in the cylindrical settling column to generate quasi-isotropic turbulence flow. The experiments were carried out to clarify the influences of turbulence on cohesive sediment flocculation and settling in salt water and fresh water. The floc size distribution，volume fraction and suspended sediment concentration were analyzed based on the experimental results. The results show that the flocculation time is shorter and the floc size is larger in salt water than those in fresh water. However，the effect of salinity on the floc volume fraction is not obvious under the same shear rate conditions. The maximum floc size firstly increases，then decreases with increasing shear rate. When the maximum floc size is formed，the shear rates are 20.8,s-1and 15.6 s-1in salt water and fresh water，respectively. Furthermore，with the increase of the shear rate，the sediment equilibrium concentration increases and the time required for equilibrium decreases.

oscillating grid；turbulent shear；salinity；cohesive sediment；flocculation and settling；sediment concentration

TV142

：A

：0493-2137(2014)09-0811-06

10.11784/tdxbz201303022

2013-03-10；

2013-04-07.

国家自然科学基金资助项目(50909071)；湖南省水沙科学及水灾害防止重点实验室开放基金资助项目(2010SS01).

乔光全（1986— ），男，博士研究生.

张金凤，jfzhang@tju.edu.cn.

时间：2013-11-18.

http：//www.cnki.net/kcms/detail/12.1127.N.20131118.1632.002.html.