多孔孔板流量计流场仿真

于洪仕，张 涛，赵珊珊，蒋 伟

(1. 天津大学电气与自动化工程学院，天津 300072；2. 辽宁工程技术大学电子与信息工程学院，葫芦岛 125105)

多孔孔板流量计流场仿真

于洪仕1,2，张 涛1，赵珊珊1，蒋 伟1

(1. 天津大学电气与自动化工程学院，天津 300072；2. 辽宁工程技术大学电子与信息工程学院，葫芦岛 125105)

为准确计算多孔孔板流量计流场，采用Standard-kω模型、SST(剪切应力传输) -kω模型、Standard k-ω+ SST k-ω(Standard k-ω模型的计算结果作为SST-kω模型仿真计算的初始值)组合模式分别对100,mm口径、节流比为0.6的3种结构多孔孔板流量计流场进行数值计算，并结合射流理论以及实流实验结果对数值计算结果进行分析．结果表明：对于中心节流孔与环形排列孔之间距离较小的多孔孔板，SST-kω模型收敛性较好；反之，SST-kω模型计算结果收敛困难，Standard-kω+SST-kω组合模式在保证计算精度的前提下改善了收敛效果．相对于Standard-kω模型，SST-kω模型更适合计算多孔孔板流量计的流场，计算结果符合射流理论，能反映出不同多孔孔板流出系数线性度的差异，与实流实验结果的最大误差为4.2%．

多孔孔板；流出系数；湍流模型；仿真

多孔孔板流量计是一个对称的多孔圆盘，是在标准孔板基础上发展起来的非标准节流装置．2006年该流量计被引入中国市场，开始应用于天然气、化工、炼油等工业领域．从相关文献[1-3]可以看出该流量计具有比标准孔板更为出色的计量性能，如测量精度高、量程范围宽、压力损失小、前后直管段要求低等优点．多孔孔板流量计结构参数多，如节流孔的大小、个数及排列方式等，优化结构参数是提高多孔孔板流量计性能的前提条件．实现这一研究有实流实验和数值模拟2种方法．数值模拟方法是研究流量传感器特性的有效手段之一，既可降低成本，又可提高效率．目前，关于对多孔孔板流量计流场仿真方法的研究国内外尚鲜见文献报道．

因此，笔者在对多孔孔板流量计的研究过程中引入该方法，一方面可以加速研究进程，另一方面通过选择合适的计算模型提高多孔孔板流量计流场计算的准确性．

1 湍流模型的选择

由于目前尚无对流场具有普适性的湍流模型，科研人员只能根据流场概况选择相对合理的湍流模型．在近几年的研究中，-kω湍流模型被广泛应用，吴军等[4]采用SST-kω模型对汽车绕流仿真；EIBehery等[5]采用Standard-kω模型对二维非对称扩散器进行仿真；Garg等[6]利用SST-kω对跨音速涡轮叶片上热量传递进行仿真．上述研究取得较好的效果，这说明双方程形式的-kω模型在计算近壁区流场、含有尾涡及剪切层等流场具有较好的计算效果．

由于多孔孔板孔分布具有分散性，流体经过多孔孔板后在管道中形成受限性多股射流．射流自孔口出射后与周围静止流体间形成速度不连续的间断面，速度间断面是不稳定的，必定会产生波动，并发展成漩涡，从而引起紊动．这样就把原来周围处于静止状态的流体卷吸到射流中，形成射流的卷吸现象[7]．根据文献[7]中的双股射流理论，流体经过多孔孔板后多股射流间形成会聚区，最终合而为一进入联合区．由于卷吸现象的存在，会聚区内形成射流间回流区，各股射流与壁面之间产生近壁面回流区，在壁面回流区和射流间回流区中有大量的漩涡存在，流场如图1所示．

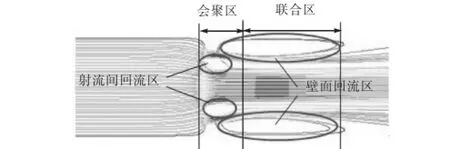
图1 多孔孔板流场示意Fig.1 Flow field of multi-hole orifice

由于射流与周围静止流体的卷吸与掺混，相应地产生了对射流的阻力，使射流边缘部分流速降低，难以保持原来的初始流速．射流与周围流体的掺混自边缘部分向中心发展，经过一定的距离发展到射流中心，自此以后射流的全断面上都发展成湍流．由孔口边界开始向内外扩展的掺混区即为剪切层，因此，流体经过多孔孔板形成的多股射流流场中存在较多的剪切层．综上所述，多孔孔板流量计的流场情况较为复杂，这就要求湍流计算模型对含有大量漩涡及剪切层的流场具有较好的计算效果；由于多孔孔板流量计采用壁面取压方式，该取压方式要求湍流计算模型对近壁区域有较好的计算效果．

基于上述两方面原因，本研究采用双方程形式的Standard-kω模型、SST-kω模型以及Standard-kω+ SST-kω组合形式分别对10块100,mm口径、β= 0.6的多孔孔板进行了数值模拟与实流实验，流速范围为0.5～7.5,m/s．本文选择了其中3块具有代表性的多孔孔板对研究结果进行说明．

2 湍流模型

Standard-kω模型是一个通用双方程湍流模型[8-9]，其中一个变量是湍动能k，另一个变量为耗散率ω．Standard-kω模型是基于Wilcox-kω模型，该模型对近壁区域的流动、尾流、射流、剪切层及低雷诺数流动有较好的预测效果．SST-kω模型是由Menter提出的双方程湍流模型，该模型不但集成了Standard-kω模型特点与Standard -kω模型对高雷诺数流动具有较好计算效果的优点，而且增加了横向扩散导数项，在湍流黏度定义中考虑了湍流剪切应力的传输过程．其模型为

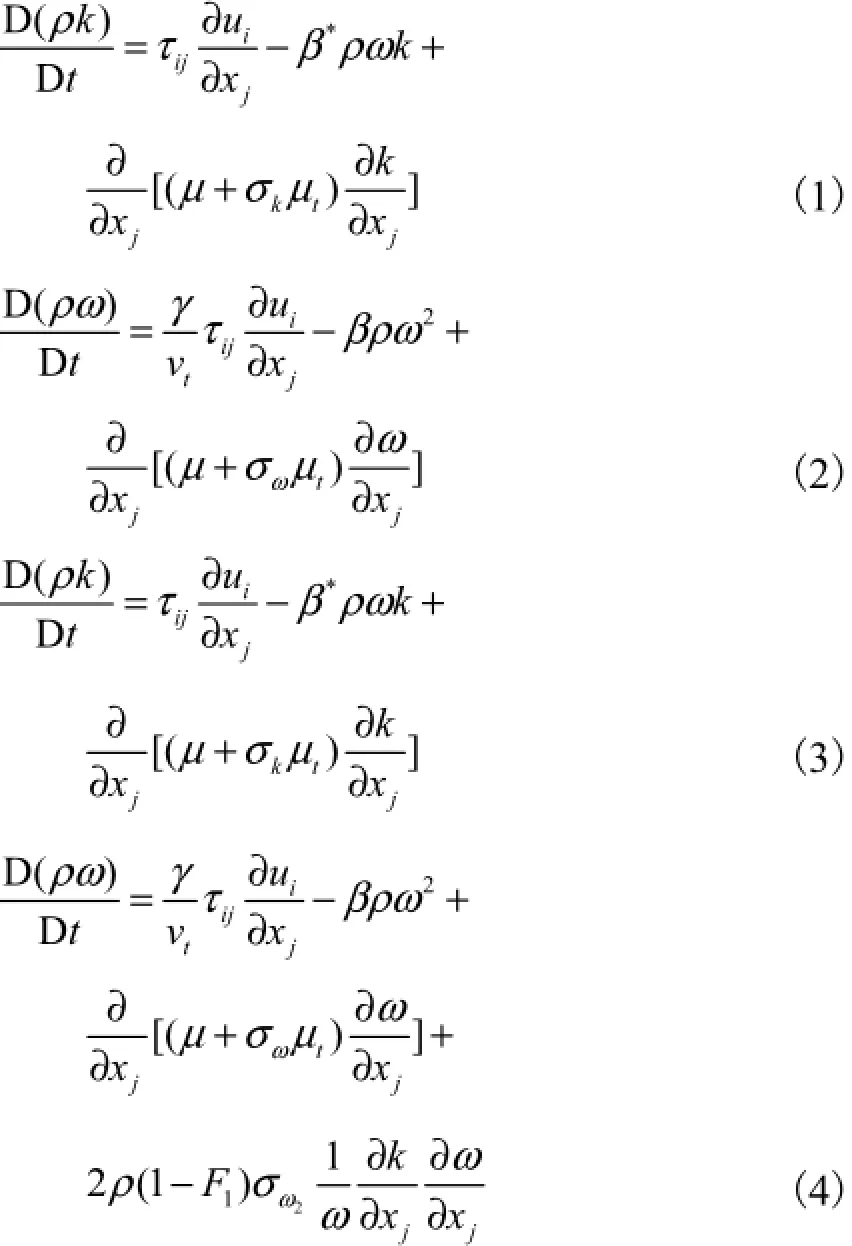
其中

3 建模网格剖分

3.1 多孔孔板流量计的几何结构

图2为多孔孔板流量计结构，其中图2(a)为流量计的整体结构，图2(b)为多孔孔板的结构及参数定义．图2(b)中D为多孔孔板流量计的管径；D1为中心节流孔直径；D2为环状排列孔直径；D3为环状排列孔的中心圆直径；多孔孔板中心节流孔与环形排列孔之间的距离为d1，环形排列孔与管壁之间的距离为d2．图3为多孔孔板实验样机，d1、d2的大小决定了射流间回流区及壁面回流区的尺寸，因此表1中给出了各样机的d1、d2的具体数值．

图2 多孔孔板流量计结构Fig.2 Structure of multi-hole orifice flow meter

图3 多孔孔板实验样机Fig.3 Experimental prototype of multi-hole orifice

3.2 网格剖分

按照流量计的实际尺寸在GAMBIT中建立三维计算模型，前直管段长度设置为10倍管径，后直管段长度设置为30倍管径．为了准确获得多孔孔板附近的流场变化情况，多孔孔板附近采用size function函数进行加密处理，特别在多孔孔板的下游，加密区域更大，而在远离多孔孔板的上下游直管段区域的网格逐渐变得稀疏，最密处网格尺寸与两侧稀疏处的比为1∶5．网格质量为EquiSize Skew值为0.75，EquiAngle Skew值为0.80，Aspect Ratio值为1.0∶3.4．图4为多孔孔板B仿真模型局部网格．

表1 实验样机的几何参数Tab.1 Geometric parameters of experimental prototype

图4 多孔孔板仿真模型局部网格Fig.4 Gridding shape in simulation of multi-hole orifice

4 计算结果分析

衡量湍流模型对节流式流量计数值计算效果优劣标准如下.

(1)在同样的流量范围内，比较数值计算得出的流出系数C与实流实验结果是否具有一致性；

(2)通过对不同物理量的流场分析，判断计算结果是否与相应流体力学理论一致.

4.1 流出系数C的计算结果与分析

节流式流量计测量不可压缩流体的体积流量计算公式为

式中：qV为体积流量，m3/s；Δp为上下游取压点测得的差压值，Pa，在仿真实验中，来自流场数值计算结束后压力场数据的提取，在实流实验中则直接来自差压变送器的读数；ρ为流体的密度，kg/m3；β与d分别是多孔孔板的等效直径比和节流孔的等效直径，在实验中均为确定的几何参数；C为节流式流量计的流出系数，该参数是从仿真计算或者是实流实验中得出，因此节流式流量计的流出系数C是评价节流式仪表性能的最重要参数．

为了便于书写，Standard-kω、SST-kω、Standard-kω+SST-kω分别采用如下缩写形式：STD、SST、STD+SST．图5～图7是STD模型、SST模型及STD+SST组合形式在同一雷诺数范围内对不同结构的多孔孔板流量计计算得出的流出系数C值和实流实验值(EXP)的比较．每个湍流模型的8个仿真实验点对应入口流速分别为0.5,m/s、1.0,m/s、2.0,m/s、3.0,m/s、4.0,m/s、5.0,m/s、6.0,m/s和7.5,m/s．

在数值计算过程中，对于多孔孔板A、B，SST模型在计算过程中发散．从图5～图7可以看出，在这3种数值计算方式中，SST模型或STD+SST模式计算得到的流出系数C在变化趋势与实流实验结果吻合得最好；STD模型计算得到的流出系数C的变化趋势与实流实验之间有轻微的差异，但总体趋势一致．

图5 多孔孔板A仿真结果与实验结果比较Fig.5 Comparison of the results between simulations and experiments of multi-hole orifice A

图6 多孔孔板B仿真结果与实验结果比较Fig.6 Comparison of the results between simulations and experiments of multi-hole orifice B

图7 多孔孔板C仿真结果与实验结果比较Fig.7 Comparison of the results between simulations and experiments of multi-hole orifice C

表2和表3中定量地给出了采用各数值计算方法得出的计算结果．表2中定量地给出了采用各数值计算方法得到的流出系数平均值、实流实验得出的流出系数平均值及其平均值相对误差，该误差定义为

表3中定量地给出了采用各数值计算方法得到流出系数线性度ELA以及实流实验得出的流出系数线性度ELE，计算流出系数线性度的表达式为

式中：Cmax为所有流量点中流出系数最大值；Cmin为所有流量点中流出系数最小值．

表2 不同数值计算方法计算的多孔孔板流出系数结果比较Tab.2Comparisons of calculating discharge coefficient of multi-hole orifice using different models

表3 不同数值计算方法计算的多孔孔板流出系数线性度结果比较Tab.3Comparisons of calculating discharge coefficient linearity of multi-hole orifice using different models

从表2中可以看出，对于多孔孔板C，3种计算模式均收敛，STD模型计算结果的相对误差为6.90%，SST模型与STD+SST模式计算结果的相对误差较小，分别为4.30%与4.20%．对于多孔孔板A与B，STD模型与STD+SST模式计算结果的相对误差均较小，其中STD+SST模式对多孔孔板计算结果的相对误差随着d2值的减小而减小．从表3中可以看出，利用STD+SST模式计算多孔孔板可以较好地反映出不同形式多孔孔板的流出系数线性度．

4.2 不同物理量流场分析

图8 多孔孔板A的速度云图(STD)Fig.8 Velocity nephogram of multi-hole orifice A(STD)

图9 多孔孔板A的速度云图(SST)Fig.9 Velocity nephogram of multi-hole orifice A(SST)

图10 多孔孔板B的速度云图(STD)Fig.10 Velocity nephogram of multi-hole orifice B(STD)

图11 多孔孔板B的速度云图(STD+SST)Fig.11 Velocity nephogram of multi-hole orifice B(STD+SST)

(1) 从上述分析可知，分别用STD湍流模型和STD+SST组合模式计算多孔孔板A、B得出的流出系数计算结果与实流实验结果相对误差均较小，但是速度场和湍流强度场却有很大差别，如图8～图13所示．Standard k-ε 湍流模型对高雷诺数湍流及具有自由剪切层的湍流具有很好的计算效果，SST模型中集成了Standard k-ε 湍流模型的这一优点，所以利用STD+SST模式仿真多孔孔板A得到的下游速度流场具有明显的会聚趋势，符合文献[4]中的双股理论，而利用STD仿真多孔孔板A得到的下游射流没有明显会聚趋势．多孔孔板B的速度场云图虽然符合射流理论，但是利用STD+SST模式计算的湍流强度场中湍流强度最大的位置在射流的剪切层中，与文献[10]结论一致．因此可以看出SST湍流模型比STD湍流模型更适合计算受限性多股射流相互作用的流场．

(2) 从图9、图11和图14中可以看出，相对于多孔孔板C，多孔孔板A、B的射流间回流区域较大，壁面回流区域较小．直接使用SST模型计算射流间回流区域较大多孔孔板时的收敛比较困难，而STD+SST组合模式不但克服了上述缺点并且计算效果较好．

图12 多孔孔板B的湍流强度云图(STD)Fig.12 Turbulence intensity nephogram of multi-hole orifice B(STD)

图13 多孔孔板B的湍流强度云图(STD+SST)Fig.13 Turbulence intensity nephogram of multi-hole orifice B(STD+SST)

图14 多孔孔板C的速度云图(SST)Fig.14 Velocity nephogram of multi-hole orifice C(SST)

(3)如前文所述，SST模型在近壁区以外及剪切层中集成了Standard k-ε 湍流模型的特点，而Standard k-ε 湍流模型本身存在缺陷，该模型在弯曲壁面、弯曲流线等情况下会产生失真．多孔孔板A、B、C的壁面回流区依次增大，所以采用壁面取压方式时，计算得出流出系数平均值与实流实验得出的流出系数平均值之间的相对误差依次减小．

5 结 语

通过有限体积法数值求解Reynolds平均N-S方程，湍流模型分别用STD模型、SST模型及STD+ SST组合模式对3块多孔孔板流量计进行了数值模拟．结果表明：对于中心节流孔与环形排列孔之间距离较小的多孔孔板，SST模型收敛性较好；对于中心节流孔与环形排列的小孔之间距离较大的多孔孔板，SST模型计算结果收敛困难，STD+SST组合模式在保证计算精度的前提下改善了收敛效果．相对STD模型，SST模型更加适合计算多孔孔板流量计的内部流场，计算结果与射流力学中的双股射流理论一致，与实流实验结果误差的最大值为4.2%，并且能反映出不同多孔孔板流出系数线性度的差异．因此，利用该方法计算多孔孔板流场对优化多孔孔板结构具有一定的指导意义，并且对其他具有射流性质的流场仿真具有一定的参考价值．

［1］ 周 人. A+K平衡流量计的独特性能和典型应用[J].医药工程设计，2011，32(3)：54-57.

Zhou Ren. Unique characteristic and typical application of A+K balanced flow meter[J]. Pharmaceutical and Engineering Design，2011，32(3)：54-57(in Chinese).

［2］ 马太义，王 栋，张炳东，等. 多孔板流量测量的实验研究[J]. 核动力工程，2010，31(2)：126-130.

Ma Taiyi，Wang Dong，Zhang Bingdong，et al. Experimental on metering characteristics of multi-hole orifice[J]. Nuclear Power Engineering，2010，31(2)：126-130(in Chinese).

［3］ Zhao Tianyi，Zhang Jili. Experimental investigation of key parameters pertinent to multi-hole orifice throttling characteristic[J]. Journal of Harbin Institute of Technology：New Series，2008，15(1)：9-12.

［4］ 吴 军，谷正气，钟志华. SST湍流模型在汽车绕流仿真中的应用[J]. 汽车工程，2003，25(4)：326-329.

Wu Jun，Gu Zhengqi，Zhong Zhihua. The application of SST turbulence model in the aerodynamic simulation of the automobile[J]. Automobile Engineering，2003，25(4)：326-329(in Chinese).

［5］ EI-Behery S M，Hamed M H. A comparative study of turbulence models performance for separating flow in a planar asymmetric diffuser[J]. Computers and Fluids，2011，44(1)：248-257.

［6］ Gary V K，Ameri A A. Two-equation turbulence models for prediction of heat transfer on a transonic turbine blade[J]. Heat and Fluid Flow，2001，22(6)：593-602.

［7］ 董志勇. 射流力学[M]. 北京：科学出版社，2005.

Dong Zhiyong. Jet Mechanics[M]. Beijing：Science Press，2005(in Chinese).

［8］ Bakabel A，Hegab A M，Nasr M，et al. Assessment of turbulence modeling for gas flow in two dimensional convergent-divergent rocket nozzle[J]. Applied Mathematical Modelling，2011，35：3408-3422.

［9］ Qiu Yunming，Liu Zuyuan，Chen Xide，et al. Numerical calculation of maneuvering hydrodynamic forces of drift ship based on SST κ-ω turbulence model[C] // The 2nd International Conference on Computer Engineering and Technology. Chengdu，China，2010：285-288.

［10］ Fujisawa N，Nakamura K，Srinivas K. Interaction of two parallel plane jets of different velocities[J]. Journal of Visualization，2004，7(2)：135-142.

(责任编辑：孙立华)

Simulation of the Flow Field of Multi-Hole Orifice Flow Meter

Yu Hongshi1,2，Zhang Tao1，Zhao Shanshan1，Jiang Wei1
(1. School of Electrical Engineering and Automation，Tianjin University，Tianjin 300072，China；2. School of Electronic and Information Engineering，Liaoning Technical University，Huludao 125105，China)

In order to calculate the flow field of multi-hole orifice flow meter accurately，Standard k-ω turbulence model，SST(shear-stress transport)k-ω turbulence model and the composite pattern of Standard k-ω and SST kω (the calculation result of Standard k-ω as the original value of SST k-ω) were applied to simulate the flow field of three multi-hole orifice flow meters，each with the inside diameter of 100,mm and the equivalent diameter ratio β of 0.6，but with different structures，and the calculation result was analyzed according to the real physical experiment data and theory of jet. The result shows：for the multi-hole orifice with a short distance between the center hole and the holes arrayed on the ring，the convergence of SST k-ω model is better；oppositely，the convergence of SST kω model is difficult，and the composite pattern of Standard k-ω and SST k-ω enhance effect of convergence on the premise of calculation accuracy. Relative to Standard k-ω，the SST k-ω model is more accurate and performs better in calculating flow field of multi-hole orifice，the calculation result conforms to the theory of jet and shows the difference of linearity of different multi-hole orifices，and the maximum deviation between calculation result and real physical experiment result is 4.2%.

multi-hole orifice；discharge coefficient；turbulence model；simulation

TH814

A

0493-2137(2014)01-0061-06

10.11784/tdxbz201207058

2012-07-21；

2012-10-22.

于洪仕（1980— ），男，博士研究生，yuhongke_2004@163.com.

张 涛，zt50@tju.edu.cn.