TiH2脱氢规律与动力学计算

曹杰义，肖平安，戴坤良，李晨坤，张 霞

(湖南大学 材料科学与工程学院，长沙 410082)

TiH2是钛的一种氢化物，晶格类型为面心立方，属于CaF2结构，在常温时化学性质稳定，加热后分解，释放出氢气，变成纯钛。近年来，随着对这种金属型氢化物的研究逐渐深入，其应用范围也越来越广阔。在泡沫铝的生产中，TiH2粉末作为理想的发泡剂，已被广泛应用[1]；在粉末冶金生产中，将TiH2粉末与合金粉末混合，可以生产出需要的钛合金产品[2−3]；关于这种材料作为未来储氢与电池材料的研究也方兴未艾[4−5]。

TiH2在加热过程中的分解行为和脱氢规律一直是研究人员的研究重点，主要方向则集中在其作为泡沫铝发泡剂的使用及钛粉末冶金领域[6−9]。JIMÉNEZ等[10]研究了 TiH2粉末在不同气氛脱氢和吸氢时晶体结构的演变规律，并结合平衡相图得到TiH2颗粒随径向深度变化的相变化模型。ERSHOVA等[11]采用等压热分析设备对球磨20 min后的TiH2粉末进行等温加热和冷却，仪器记录下整个过程中氢气体积变化量曲线。与球磨前的粉末相比，球磨后粉末的焓降低了73 kJ/mol，且相转变温度点也有所下降。BORCHERS等[12]采用DSC技术测试了TiH2的几个吸热峰，将准备好的粉末加热到每个吸热峰结束温度时再快速冷却，使相结构得以保留，得出了氢化钛的脱氢步骤TiH1.92→TiH2−x→ Ti(H)→{TiH2−x+ TiH+Ti(H)}→Ti。

以上研究包含了近年TiH2研究的主要方向，多采用实验方法探索其脱氢相变规律。本文作者首先用DSC/TG/DTG与XRD检测手段得到TiH2脱氢的相变步骤，再从动力学角度出发，运用几种经典热分析动力学计算方法研究TiH2热分解相变、反应模型与活化能，提出TiH2热分解行为比较合理的热分析动力学研究方法。

1 实验

1.1 XRD谱

将 TiH2粉末压制成块状压坯，放入管式烧结炉中，炉管中通过2 L/min的高纯流动氩气(99.999%)，开始以 5 ℃/min的升温速率分别升温到 400、460、500、600、660、680和 700 ℃，在预定温度保温 10 min后在氩气保护下淬火，磨去试样表面氧化层后采用X射线衍射仪检测其相组成。

实验所用TiH2粉末粒度范围是63～75 μm，氧含量低于 0.34%(质量分数)，氮含量低于 0.57%(质量分数)。X射线衍射仪为D8−advance，Cu靶石墨单色器Kα辐射X射线衍射。气氛烧结炉是合肥科晶材料技术有限公司生产的GSL1600型纳米管真空烧结炉。

1.2 TG/DSC检测

使用德国Netzsch公司生产的Sta 449C同步差热分析仪进行TG和DSC检测，在100 mL/min的高纯氩气流中将TiH2粉体分别以10、20和30 ℃/min的加热速率从室温加热到900 ℃。

2 结果与讨论

2.1 TiH2热分解规律

图1 TiH2在不同温度下加热10 min后的XRD谱Fig. 1 XRD patterns of TiH2 at different heating temperatures for 10 min

图1 所示为TiH2原料粉和TiH2压坯在氩气气氛中于不同温度下加热处理10 min后的XRD谱。从上到下依次是700、680、660、600、500、460和400 ℃的热处理坯样衍射谱线和TiH2原料粉的衍射谱线。Ti有多种金属氢化物，其中大部分为面心立方晶体结构，它们的衍射峰值比较接近。由 TiH2原料粉末的XRD谱可以看出，其d值与TiH1.97的最接近。在氩气气氛中将压坯加热到400 ℃时，其衍射峰变宽，到500 ℃时衍射峰又变窄，但衍射角已向高角度偏移。与标准图谱对比可知，氢化物已转变为 TiH1.5，这表明500 ℃时TiH1.97已完全转变为TiH1.5，温度低于500 ℃时是这两种氢化物的混合物。500 ℃时衍射谱线在 2θ为30°～40°之间的位置出现了部分α-Ti衍射峰，说明在此温度下部分氢化物已转变成Ti，成为TiH1.5与Ti的混合物加热温度。到600 ℃时，α-Ti衍射峰明显加强，TiH1.5衍射峰依然存在。当温度升高到 660 ℃时，衍射谱主要是α-Ti 衍射峰，加热到700 ℃后，仅有Ti衍射峰。由此说明坯样在500～700 ℃之间发生了TiH1.5向Ti的转变。

图2所示为TiH2粉末以10 ℃/min升温速率升温时测定的DSC/TG曲线。可以明显看到，在升温过程中有两个分离的吸热峰，通过标定与计算得到第一个吸热峰的温度范围是436～526 ℃，样品质量损失率约为0.8%；第二个吸热峰的温度范围是526～666 ℃，样品质量损失率约为 2.9%，总过程质量损失率约为3.7%，较TiH2的理论脱氢率(4.0%)略低，这可能与氢在钛中的固溶、原料的纯度、仪器误差及氧化有关。第一个吸热峰样品质量损失率约为 0.8%，与 TiH2转变成 TiH1.5的质量损失率(1%)相当；第二个吸热峰样品质量损失率约为2.9%，与TiH1.5转变成Ti的质量损失率(3%)相当。

由此可知，TiH2的 XRD测试结果基本反映了其DSC/TG曲线原位连续分解的成分变化规律。即TiH2粉体在氩气气氛中加热分解基本分3步完成，分别是TiH2→TiH1.5、TiH1.5→Ti(固溶)和 Ti(H 固溶)→Ti。

图2 TiH2的DSC/TG曲线Fig. 2 DSC and TG curves of TiH2

2.2 TiH2热分析动力学计算

从前面的分析知，TiH2→Ti的转变分3步完成，前两步是化合态氢化钛的分解，最后一步是氢在固溶体中的脱除。体现在DSC/TG曲线中则是3个变化阶段，图2表示TiH2分解的典型DSC/TG曲线，将不同温度下的TG曲线分别划分为3个阶段，第一阶段与第二阶段以 dα/dT(脱氢分数对温度的微分)的最高峰为分界点，第二阶段与第三阶段以第二阶段DSC峰完结处作为分界点，便可得不同升温速率下 TG曲线 3个阶段的温度区间，将其列于表1。

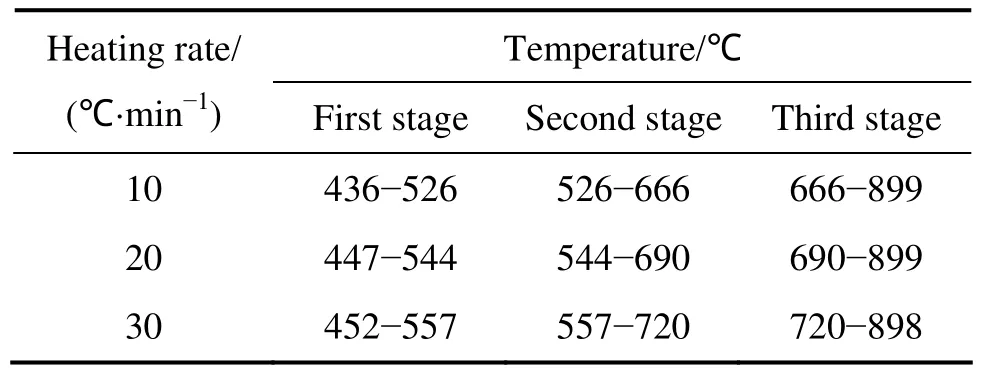
表1 不同升温速率下TiH2的TG曲线的3个阶段Table 1 Three stages of TG curve of TiH2 at different heating rates

将TG曲线的3个阶段视为3个独立的分解阶段，m0为每个阶段的初始质量，Δmt为该阶段总质量损失，m为温度T时的质量，α=(m−m0)/Δmt×100%表示分解率，通过计算得到每个阶段的分解率随温度变化的规律，即图3所示的3组曲线。将图3中的曲线进行微分处理，得到各个阶段的DTG曲线(见图4)。

图3和4分别为不同升温速率下TiH2在各分解阶段的分解率α和DTG曲线，图中各阶段的曲线从左至右升温速率分别为10、20和30 ℃/min。可以看到，随着升温速率的提高，TiH2脱氢的起始温度和结束温度都相应提高(见图3)。DTG 曲线有一个共同的规律：随着温度升高，分解速率首先逐渐增大，在某一温度值达到最大值，然后减小，升温速率越快，最大分解速率dα/dT越小(见图 4)。

图3 不同升温速率下TiH2 3个脱氢阶段的分解率变化曲线Fig. 3 Decomposition rate curves of three dehydrogenation stages of TiH2 at different heating rates

图4 不同升温速率下TiH2 3个脱氢阶段的DTG曲线Fig. 4 DTG curves of three dehydrogenation stages of TiH2 at different heating rates

DSC/TG分析是一种测定样品整体物理性质(能量、质量)随温度和时间变化的技术，因此表征反应进度的α也只是一个表观、综合的概念，如果一个反应实际上包含了多个基元反应，就无法将这种物理量合理地分解成某个基元反应的贡献[13]，固态反应往往是多个基元反应平行、部分重叠或递次发生的过程，这是由非均相反应体系本身的复杂性决定的。多年来，研究人员针对这个问题，提出了无数的处理方法。这些方法从数学上分为积分法和微分法，从操作方法上分为单个扫描速率法(模式函数法)和多重扫描速率法(无模式函数法)[14]。有研究证明，对固体的多步反应机理，用多重扫描速率法和等转化率法处理比较有效[15]。

本文作者分别采用单个扫描速率法和多重扫描速率法处理TiH2热分析结果。

2.2.1 单个扫描速率法

由于反应机理与反应动力学函数是一一对应的，不同阶段的反应机理不尽相同，因此需要对不同阶段分别进行计算与分析。选取升温速率为10 ℃/min的热分析数据，用Satava-Sestak 法、Coats-Redfern法和Achar-Brindley-Sharp-Wendworth法分别计算反应的每一个阶段。

Coats-Redfern方程：

Achar-Brindley-Sharp-Wendworth方程：

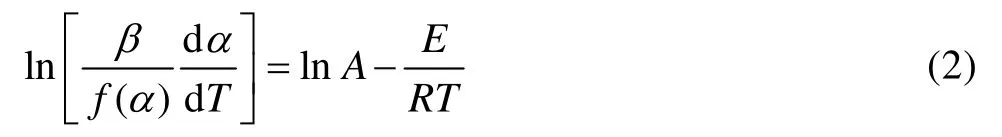
Satava-Sestak方程：

式中：α为反应分数(分解率)；G(α)为反应机理函数的积分形式；f(α)为反应机理函数；A为频率因子；E为反应活化能，kJ/mol；R为摩尔气体常数，8.314 J/(mol·K)；β为升温速率，K/min；T为反应温度，K。将图3和4中的基本数据α、T、dα/dT和常用动力学机理函数[16]代入式(1)～(3)中。通过线性回归，得到一系列E、A、线性相关系数r和标准误差SD。

参考ZHANG等[17]和HU等[18]提出的最概然机理函数的推断条件：1) 活化能为 80～250 kJ/mol，lgA为7～30；2) 线性相关系数|r|＞0.98；3) 标准误差较小(SD＜0.3)；4) 采用不同模式函数方法、同一机理函数时，动力学参数值近似相等。对比后得到TiH2→TiH1.5转变机理为球形对称边界反应，机理函数为G(α)=1−(1−α)1/3，TiH1.5→Ti(固溶)转变机理为化学反应，机理函数为G(α)=(1−α)−1，Ti(固溶)→Ti转变机理为三维球形对称扩散，机理函数为G(α)= [1−(1−α)1/3]2。

2.2.2 多重扫描速率法

多重扫描速率法避免了反应机理函数的选择而直接求出E值。与其他方法相比，它避免了因反应机理函数的假设不同而可能带来的误差。使用 Friedman-Reich-Levi法、 Kissinger-Akahira-Sunose法 和 Flynn-Wall-Ozawa法分别计算反应的每个阶段。Friedman-Reich-Levi 方程：

Kissinger-Akahira-Sunose方程：

Flynn-Wall-Ozawa 方程：

将图3和图4中的基本数据α、T和dα/dT代入方程(4)～(6)中，通过线性回归，求得表观活化能(E)及线性相关系数(r)。

图5所示为利用以上方法所求得的不同转化率时的E值。显然，3 种方法求得的活化能值及其变化规律基本一致，其中 Friedman-Reich-Levi法和Kissinger-Akahira-Sunose 法得到的值非常接近。Flynn-Wall-Ozawa法得到的部分值偏低。

图5 TiH2各脱氢阶段的表观活化能Fig. 5 Apparent activation energy of each dehydrogenation stage of TiH2: ●—Kissinger-Akahira-Sunose; ■—Friedman-Reich-Levi; ▲—Flynn-Wall-Ozawa

还可以看到，虽然3个阶段的激活能是分开计算的，但是前后连贯有规律地呈阶梯状下降，在每个阶段中随着反应的进行，表观活化能E也是逐渐降低。TiH2分解过程包括 TiH2→TiH1.5→Ti(固溶)→Ti的 3 个转变阶段，此外还包括H原子在钛表面结合成H2和H2从钛表面脱附与向外扩散。转变分解过程并非各步骤相继进行，而是有的部分重叠，同时发生。所以，计算所得活化能不是表征某一简单过程，而是表征了在不同反应阶段各个简单过程对整个反应的贡献。因此，可以从表观活化能的极值估计各简单过程的活化能[19]。

综上所述，TiH2→TiH1.5，TiH1.5→Ti(固溶)及 Ti(固溶)→Ti的相转变反应实质上是同时进行的，只是在不同阶段，某一步反应占主导地位，随着温度的升高，它们对总反应的贡献不断变化。第一阶段主要包括TiH2→TiH1.5与 TiH1.5→Ti(固溶)两个相转变反应。由于H原子很小，在钛中很容易扩散，而钛颗粒的外部是流动的氩气，H2的生成与外扩散也很容易进行，它们对整体反应速率影响不大。第一阶段最初是以TiH2→TiH1.5的相变为主，由极值可得其激活能约为240kJ/mol；随着反应的进行，活化能较低的TiH1.5→Ti(固溶)转变也开始发生，而且所占比例越来越高，TiH2→TiH1.5相变对反应的贡献逐渐减小，所以整体表观活化能持续降低。在第一阶段快结束时以TiH1.5→Ti(固溶)的相变为主，此时整体的表观活化能即其活化能，约为190 kJ/mol。同理可知，第二阶段主要是TiH1.5→Ti(固溶)与Ti(固溶)→Ti两个相转变反应。第三阶段以Ti(固溶)→Ti为主，第二阶段结束与第三阶段开始时的表观活能为其活化能，约为 145 kJ/mol。最后阶段的转变过程包含H原子的内扩散、H2的生成与外扩散，其中 H2的生成是这一阶段脱氢速率的主要控制因素，所以实质上这一阶段的表观激活能主要是H+H→H2的激活能。H原子的扩散激活能较低，对过程影响不大，所以第三阶段激活能大部分保持不变，直到快结束时才开始下降；下降过程中的激活能H原子的扩散激活能和H2的生成激活能。

3 结论

1) TiH2粉体在氩气气氛中加热分解分3步完成：第一步 TiH2→TiH1.5转变机理为球形对称边界反应；第二步TiH1.5→Ti(固溶)转变机理为化学反应；第三步Ti(固溶)→Ti转变机理为三维球形对称扩散。TiH2→TiH1.5和 TiH1.5→Ti(固溶)、Ti(固溶)→Ti相转变的活化能分别为240、190和145 kJ/mol。

2) 单个扫描速率法的目标是以整个分解过程确定一个机理函数、提取一个E值和A值，而TiH2分解过程比较复杂，同时涉及多个转变过程，随着反应的进行，控制速率的主要环节或进程在不断渐变，当只有一种机理在过程中占主导地位时，单个扫描速率法才比较适合。多重扫描速率法在不考虑机理的条件下不仅非常明显地展示了活化能与 TiH2分解程度的关系，而且通过对E−α曲线形状的分析，还可以大致了解不同反应进程在不同阶段对分解的贡献情况。因此，对于研究TiH2分解动力学，多重扫描速率法比较合适。

[1]杨东辉, 何德坪, 杨上闰. 氢化钛热分解反应动力学及铝合金熔体泡沫化研究[J]. 中国科学(B辑): 化学, 2004, 34(3):195−201.YANG Dong-hui, HE De-ping, YANG Shang-run. Thermal decomposition kinetics of titanium hydride and aluminum alloy melt foaming research[J]. Science in China (Series B):Chemistry, 2004, 34(3): 195−201.

[2]张家敏, 易健宏, 雷 霆. TiH2粉末制备钛合金的烧结脱氢规律及工艺[J]. 科技导报, 2012, 30(1): 65−68.ZHANG Jia-min, YI Jian-hong, LEI Ting. Dehydrogenation and sintering process of titanium hydride for manufacture titanium and titanium alloy[J]. Technology Review, 2012, 30(1): 65−68.

[3]喻 岚, 李益民, 邓忠勇, 李笃信. TiH1.924-Al-Nb混合粉球磨过程中物相变化研究[J]. 湖南冶金, 2004, 32(5): 17−19.YU Lan, LI Yi-ming, DENG Zhong-yong, LI Du-xin.TiH1.924-Al-Nb mixed powder milling process of phase change[J].Hunan Metallurgy, 2004, 32(5): 17−19.

[4]DHAOU H, MELLOULI S, ASKRI F, JEMNI A, NASRALLAH S B. Experimental and numerical study of discharge process of metal-hydrogen tank[J]. International Journal of Hydrogen Energy, 2007, 32(12): 1922−1926.

[5]CHANWOO P, TANG X D, KWANG K J, JOSEPH G, QUINN L. Metal hydride heat storage technology for directed energy directed weapon systems[C]//Proceedings of IMECE’07.Washington DC, 2007.

[6]王耀奇, 张 宁, 任学平, 侯红亮, 王宝伟. 氢化钛的动态分解行为与规律[J]. 粉末冶金材料科学与工程, 2011, 16(6):795−798.WANG Yao-qi, ZHANG Ning, REN Xue-ping, HOU Hong-liang,WANG Bao-wei. Behavior and rule of titanium hydride dynamic decomposition[J]. Materials Science and Engineering of Powder Metallurgy, 2011, 16(6): 795−798.

[7]MATIJASEVIC-LUX B, BANHART J, FIECHTER S, GORKE O, WANDERKA N. Modification of titanium hydride for improved aluminium foam manufacture[J]. Acta Materialia,2006, 54: 1887−1900.

[8]罗洪杰, 吉海宾, 杨国俊, 姚广春. 氢化钛的分解行为及其在制备泡沫铝中的应用[J]. 东北大学学报: 自然科学版, 2007,28(1): 87−90.LUO Hong-jie, JI Hai-bin, YANG Guo-jun, YAO Guang-chun.Decomposition behavior of TiH2and its application to fabricating aluminum foam[J]. Journal of Northeastern University: Natural Science, 2007, 28(1): 87−90.

[9]ZEPPELIN F V, HIRSCHER M, STANZIDE H, BANHART J.Desorption of hydrogen from blowing agents used for foaming metals[J]. Composites Science and Technology, 2003, 63:2293−2300.

[10]JIMÉNEZ C, GARCIA-MORENO F, PFRETZSCHNER B,KLAUS M, WOLLGARTEN M, ZIZAK I, SCHUMACHER G,TOVAR M, BANHART J. Decomposition of TiH2studied in situ by synchrotron X-ray and neutron diffraction[J]. Acta Materialia,2011, 59: 6318−6330.

[11]ERSHOVA O G, DOBROVOLSKY V D, SOLONIN Y M,KHYZHUN O Y. Hydrogen-sorption and thermodynamic characteristics of mechanically grinded TiH1.9as studied using thermal desorption spectroscopy[J]. Journal of Alloys and Compounds, 2011, 509: 128−133.

[12]BORCHERS C, KHOMENKO T I, LEONOV A V,MOROZOVA O S. Interrupted thermal desorption of TiH2[J].Thermochimica Acta, 2009, 493: 80−84.

[13]VYAZOVKIN S. Kinetic concepts of thermally stimulated reactions in solids: A view from a historical perspective[J]. Int International Reviews in Physical Chemistry, 2000, 19(1):45−60.

[14]BROWN H E. Introduction to thermal analysis: Techniques and applications[M]. London: Chapman and Hall Ltd, 1988: 127.

[15]BROWN M E, MACIEJEWSKI M, VYAZOVKIN S,NOMEN R, SEMPERE J, BURNHAM A, OPFERMANN J,STREY R, ANDERSON H L, KEMMLER A, KEULEERS R,JANSSENS J, DESSEYN H O, LI C R, TANG T B, RODUIT B,MALEK J, MITSUHASHI T. Computational aspects of kinetic analysis. Part A: The ICTAC kinetics project—Data, methods and results[J]. Thermochimca Acta, 2000, 355: 125−143.

[16]胡荣祖. 热分析动力学[M]. 北京: 科学出版社, 2008: 151.HU Rong-zu. Thermal analysis kinetics[M]. Beijing: Science Press, 2008: 151.

[17]ZHANG T L, HU R Z, LI F P. A method to determine the non-isothermal kinetic parameters and select the most probable mechanism function using a single non-isothermal DSC curve[J].Thermochimica Acta, 1994, 244: 177−184.

[18]HU R Z, YANG Z Q, LI Y J. The determination of the most probable mechanism function and three kinetic parameters of exothermic decomposition reaction of energetic materials by a single non-isothermal DSC curve[J]. Thermochimica Acta, 1988,123: 135−151.

[19]VYAZOVKIN S. Conversion dependence of activation energy for model DSC curves of consecutive reactions[J].Thermochimica Acta, 1994, 236: 1−13.