基于蚁群-关键链的资源受限项目调度
2014-06-02宫丽娜
宫丽娜
(枣庄学院 信息科学与工程学院,山东枣庄277160)
资源约束下的项目调度问题 (Resource con-strained proj ect scheduling problem,RCPSP)是一类广义优化问题,主要目的是在满足项目任务的紧前关系和资源约束的条件下,优化项目的进度安排,从而最小化项目工期.传统的项目管理方法,如关键路线法 (Critical Path Method,CPM)、计划评审技术 (Program Eval uation and Review Technique,PERT)[1-4]和设计结构矩阵 (Design Str uct ure Matrix,DSM),能很好地应用于单个项目的管理,但却忽视了资源约束的存在.在资源有限的情况下,上述方法已经不能有效地对并行多项目进行管理.[5]
1 问题描述
典型资源受限的多项目调度问题 (Resource—constrained Multi—Project Scheduling Proble m,RCPSP)可以描述如下:在一个项目组内包含N个相互独立的并行项目,共包含D个任务,该项目组具有两个不消耗任何时间和资源的虚工序:虚拟开始任务和虚拟结束任务.第i个项目包含ni个任务,这N个项目共享K种可更新资源,其中第k种资源的容量为Rk.用Aij表示第i个项目中的第j个任务,其工期为dij,对第k种资源的需求量为rijk,任务的开始时间标记为Sij,结束时间标记为fij,它的所有紧前任务形成的集合记为Pij,用ai表示第i个项目的权重,在时间t时正在进行的所有任务的集合标记为It.综合上述假设和采用的符号,可以描述为以下形式:
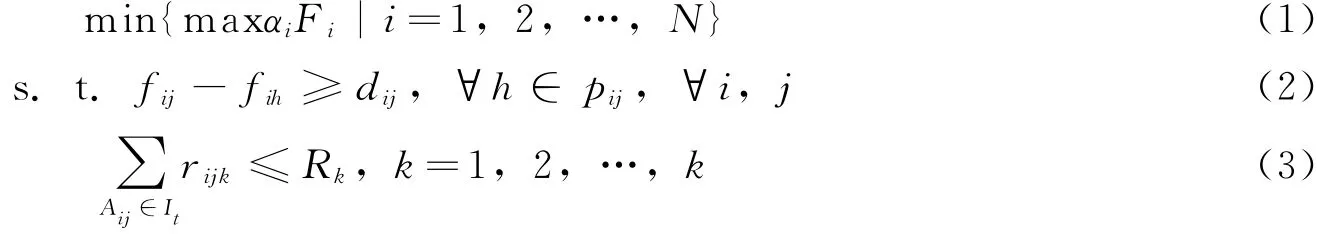
其中:Fi是第i个项目的完成时间.式 (1)表示目标函数代表项目组的总工期最短,需要通过优化使该项目标函数最小;式 (2)表示了任务间的紧前关系,一个任务没有完成之前不能开始它的任何后续任务;式 (3)则表示在任意时刻所有项目正在执行的任务对每种资源的需求总量不得超过该资源的总量.
对于多个项目中任务调度的确定,首先将各个项目的网结构图通过增加虚拟节点,合并为一个单一的网络结构图,这并不改变每个项目中任务间的关系,也不是对各个项目进行整合,而是各个项目的任务在整个新网络图中重新进行唯一标示.网络图增加两个不消耗任何时间和资源的虚拟节点用于标示整个设计过程的开始和结束:虚拟开始节点S和虚拟结束节点E作为整个设计过程唯一的开始节点和结束节点.
2 蚁群-关键链算法
2.1 蚁群优化算法 (ACO)
蚁群算法 (Ant Colony Opti mization)是由意大利学者Dorigo等人在20世纪90年代初首先提出来的.蚁群算法设计虚拟 “蚂蚁”,让他们摸索不同路线,并留下会随时间逐渐消失的虚拟 “信息素”.根据 “信息素较浓的路线更近”的原则,即可选择出最佳的路线.
通过蚁群算法构造的任务列表I=(l0,l1,…,ln+1)(其中n=ni),任务是逐个的被分配到列表I从l0到ln+1,所以每个分配可以代表蚂蚁的一次决策.当活动lr分配到列表I的r位置时,后序集Nr包含了这些活动,这些活动的紧前任务已经分配到列表中.这些后序集在构建列表过程中是逐步被修改的.在构建活动列表过程中,蚂蚁先分配l0=0,然后在每一阶段,蚂蚁都要利用信息素和启发信息在后序集Nr里选择一个活动j,使lr=j;从r=0决策到r=n.很明显,通过ACO构建的活动列表遵守优先可行性.而且当r-1个活动被选择的同时,也安排了这些活动的开始时间、结束时间以及分配给它们的资源.
2.1.2 算法描述
在每一代中存在着m个蚂蚁,每个蚂蚁都生成一个解决方案,即一个有序的活动列表,然后根据这个活动列表应用串行调度生成算法,生成调度方案.
在第一代生成时,初始化所有活动的信息素为1,然后根据启发信息和信息素的一定比例来生成活动转移概率.其中后序列表中转移概率大的被选入到活动列表.当第一代结束后,以后的每代对活动的信息素进行本地更新、蒸发和全局更新,然后进行寻找,直到找到合适的活动列表位置.
具体算法如下:
初始化
Loop
把蚁群中所有蚂蚁置于开始活动处
Loop
For 每个蚂蚁
构造可行活动集合
对活动集合中的活动进行计算,选择下一个活动
根据公式 (2)对信息素进行本地更新
将活动加入活动列表
Next
Until所有的蚂蚁都构造了一个完全可行解
使用串行调度生成方案求出每个可行解的工期
进行信息蒸发和全局信息素更新
Until满足停机条件
2.2 关键链调度方法
关键链管理方法采用关键链代替关键路径.但针对一个RCPSP,关键链数量、长度以及关键链上包含的工作集合均决定于RCPSP的求解过程.
应用关键链方法需要解决以下问题:1)活动时间消减的系数;2)在关键链的活动中设置缓存问题.
针对第一个问题,主要是应用在不受资源限制时项目的完成时间T1和受资源限制时资源的完成时间T2的比值来对活动时间进行消减,并且只消减关键链上的活动时间.[6]与使用50%的剪贴法比,使用比值的方法进行消减,使得项目活动是根据项目的具体情况进行消减的,更有效地正确估算出项目的完工时间.
针对第二个问题,对于资源缓存、对于关键链上每个活动的缓存可采用如下公式:

其中F.Tm表示缓存的大小,表示有资源限制时的活动时间,表示没有资源限制时的活动时间.
而对于全局的缓存可以采用如下公式:
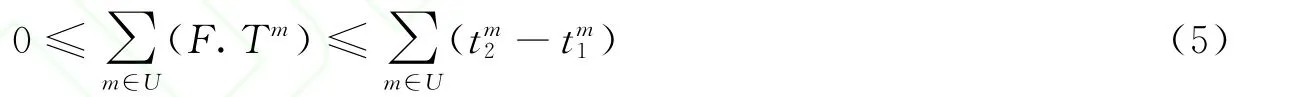
与此同时,本文还引入了两个变量系数:项目灵活系数Kp和活动灵活系数,用于更准确地确定项目的完工时间.
a)如果资源限制是由于政策因素,如由于机器太贵而决定自己生产机器等,则项目灵活系数就可以用来改变项目活动时间.

如果Kp>0,则表明考虑到战略上的原因,项目的完工时间需要延长.于是,会得到下面的式子:

如果Kp<0,则表明通过其他方法来缩短完工时间,比如增加新员工.可以得到如下式子:
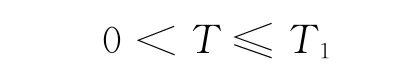
b)基于项目自身的特点,活动灵活系数可以应用于关键链的活动中来调整活动时间.通过修改,项目的完工时间可用如下公式表示:
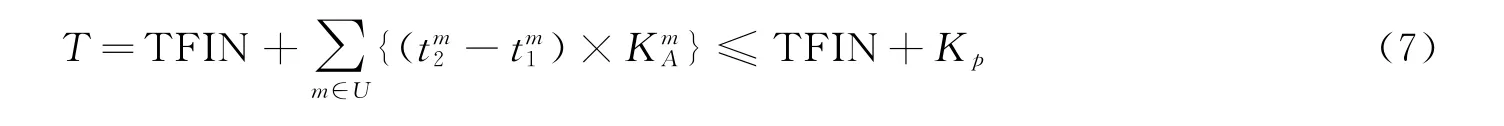
2.3 具体算法描述
在此主要介绍具体的执行算法.
第一步:计算没有资源限制时的完工时间T1,利用蚁群算法计算资源限制时项目的完工时间T2和关键链;
第二步:计算关键链活动的消减系数CR=T1/T2,并对活动时间进行消减;
第三步:利用项目灵活系数和活动灵活系数对项目的关键链完工时间进行调整;
第四步:在关键链活动的前边设置资源缓存.
3 实例分析
为了分析算法的有效性,采用文献 [7]的实例加以验证,其网络结构如图1所示.节点处的二元组分别表示工序最可能持续时间、资源R1的需求量.R1可使用量为3个单位,且工序中资源需求是不可分的.
步骤1 在资源不受限制时,关键路径为A→D→G,项目完成时间T1=9;在资源受限时,应用第三部分的蚁群算法得到关键链为:A→B→D→G→H;项目的完成时间T2=15;
步骤2 消减系数C2=T1/T2=9/15=60%,则得到新的项目网络如图2所示,项目完工时间为9;
步骤3 利用项目或者活动的灵活系数对项目或者活动时间进行调整.对于一般是利用活动在项目中的重要性及活动本身的简单性来定义的.一般取重要性和简单性系数的最大值.假设=1、=0.75=0.5、.6、=0.75,那么,项目的完成时间T=9+(2-1.2)×1+(3.5-2.1)×0.75+(3.5-2.1)×0.5+(3.5-2.1)×0.6+(2.5-1.5)×0.75=9+0.8+1.05+0.7+0.84+0.75=13.2;通过修改得到的项目网络如图3所示;

图1 项目网络图

图2 消减后的项目网络图

图3 修改后的项目网络图
步骤4 设置缓存.得到的最后结果如图3所示.
总之,资源约束下的多项目调度的算法是先通过蚁群算法找到一个合适的解,然后通过关键链的方法对可优解进行调整,以便准确地估计出项目的完工时间,主要有以下优点:
1)对于蚁群算法的启发信息主要采用了资源利用率改变量的方法;
2)用蚁群算法在安排活动时,对于具有相同活动时间的两个活动可以同时进行安排;
3)对于关键链的活动时间消减系数采用了用没有资源限制的时间T 1和有资源限制的时间T 2的比值的方法.
[1]BERMAN E B.Resource allocation in a PERT net wor k under continuous activity ti me-cost f unction[J].Manage ment Science,1964(10):734-745.
[2]ROBILLARD P.Expected co mpletion ti me in PERT net works[J].Operations Research,1976,24:177-182.
[3]LA WRENCE P,JEFFERY K.Cochran A new co mputational appr oach f or pr oject management net wor ks[J].Co mputers ind.Engng,1995,29:339-343.
[4]FATEMI GHOMI S M T,RABBANI M.A new str uct ural mechanis mfor reducibility of stochastic PERT net wor ks[J].Eur opean Jour nal of Operational Research,2003,145:394-402.
[5]施淑洪,郑荣良.电动助力转向系统及系统模型分析 [J].江苏大学学报:自然科学版,2002,23(5):57-60.
[6]Chiu-Chi Weia,Ping-Hung Liub,Ying-Chin Tsaic.Resource-constrained pr oject management using enhanced t heory of constraint[J].International Journal of Project Management,2002,20:561-567.
[7]张静文,胡信布,王茉琴.关键链项目计划调度方法研究 [J].科技管理研究,2008(3):280-283.
