加权Bergman空间上的Rudin正交性问题
2014-06-02郑桃霞徐宪民
郑桃霞,徐宪民
(1.浙江师范大学 数理与信息工程学院,浙江金华321004;2.嘉兴学院 数学研究所,浙江嘉兴314001)
本文将参照文献 [5]中的方法,利用单位圆盘上解析自映射的广义Nevanlinna计数函数,对加权Bergman空间(D)上的Rudin问题进行研究.
1 相关概念及基本符号
记C为复平面,C中开单位圆盘为D= {z:z∈C}.dA表示开单位圆盘D的规范面积测度,即dA(z)=drdθ,其中z=reiθ.

显然,当p=2时,加权Bergman空间Aα2是Hilbert空间.
定义2 对解析函数φ:D→D,定义φ的诱导测度μφ:

因此,dλφ为单位圆盘D上的有限测度.

则称μ是径向的.
如果函数f (reiθ)与θ无关,则称函数f是本性径向的.
2 引理
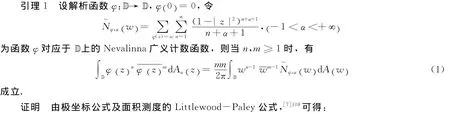
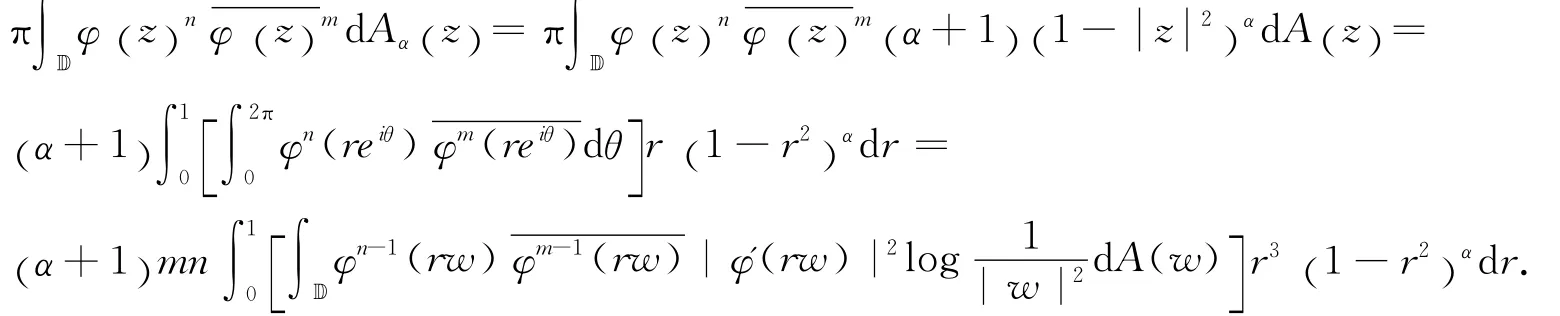
令u=rw,dA (u)=sdsdθ,则有:


引理3[5]57设φ1,φ2,…,φm是 D上的解析函数,若是径向的,则每个φk都是z的多项式.
3 主要结论

成立.
综上可知,当n≠m时,有

由上述 (b)⇒(a)证明过程可知,当n≠m时,有:


假设φ(0)=0,由littlewood不等式:[7]


对w∈φ(D)且w≠0,有


设λ0=0,于是有

从而有

[1]PAUL S BOURDON.Rudin’s orthogonality problem and the Nevanlinna counting functions[J].Proceedings of the American Mathmatical Society,1997(125):1187-1192.
[2]CARL SUNDBERG.Measure induced by analytic functions and a problem of Walter Rudin[J].Journal of the American mathematical society,2002(16):69-90.
[3]CHRISTOPHER J BISHOP.Orthogonal functions in H∞[M].Pacific Journal of.Mathematics,2005(220):1-31.
[4]GERARDO A.CHACON,JOSE GIMENEZ.Composition Operators on the Dirichlet space and related problems[J].Boletin de la Asociacion Matematica Venezolana.,2006 (2):155-164.
[5]KUNYU GUO,DECHAO ZHENG.Rudin orthogonality problem on the Bergman space[J].Journal of Functional Analysis,2011(261):51-68.
[6]KEHE ZHU.Theory of Bergman spaces[M].New York:Springer-Verlag,2000.
[7]徐宪民.复合算子理论 [M].北京:科学出版社,1999:108.
[8]WALTER RUDIN.Real and complex analysis,2nd edition[M].New York:McGraw-Hill,1974:336.
