EEMD在道路载荷谱降噪处理中的应用

李建康，宋向荣，周宏月，曾发林

(1.江苏大学 汽车工程研究院，镇江 212013;2.江苏大学 汽车与交通工程学院，镇江 212013)

在室内道路模拟试验中，作为期望响应信号的原始道路载荷谱信号(简称载荷谱)，在实际采集过程中会混入各种干扰噪声成分［1］，从而具有非平稳特征。噪声的存在会造成两大问题:① 使用雨流计数法统计时会产生虚假的应力循环［2］，影响强化道路组合的优化和整车疲劳寿命的估计;② 进行台架试验时，影响生成伺服作动器驱动信号的迭代次数和精度。因此，道路载荷谱前期需要根据车辆特性和载荷谱信号特征进行滤波降噪处理［3］。基于Fourier变换的传统频域滤波法，严格意义上而言，对于处理实质具有非平稳特征的道路载荷谱存在一定局限性［4］。

EMD［5］是一种处理非平稳非线性信号的时频分析方法，具有简单高效、自适应性强、高分辨率等优点。EEMD［6－7］是EMD方法的改进，可以抑制噪声的干扰。运用EEMD进行滤波降噪处理，已在机械、化工、土木、电力等领域得到广泛应用［8－11］。在汽车工程领域，尝试引入EEMD进行道路载荷谱信号降噪研究，具有现实工程意义与应用价值。

本文以某自卸车实测道路载荷谱为研究对象，提出了基于EEMD滤波降噪的计算步骤和原则，同EMD降噪效果进行了对比，并研究EEMD计算参数对降噪性能的影响。结果表明，EEMD可以较好地估算原始非平稳道路载荷谱中的噪声水平，可提高信噪比和应力循环次数统计的精度。

1 EEMD理论与方法

1.1 EEMD的基本理论简介

EMD是Hilbert－Huang变换的内核，已被各领域学者成功地用于处理多种非线性非平稳信号，但无法克服信号中的非白噪声干扰所引起的模态混淆现象［12］，导致分解出的固有模态函数(Intrinsic Mode Function，IMF)失真，使EMD对于包含异常事件的非平稳信号的降噪效果不佳［10］，直接影响后续的分析工作。EMD的具体步骤请参阅文献［5］。EEMD仍以EMD为基础，通过向原始信号中添加高斯白噪声进行EMD运算，最后对分解的IMF作平均处理，可解决模态混叠问题。EEMD的步骤归纳如下:

(1)通过给目标信号x(t)加上等长度的高斯白噪声w(t)，获得一个总体 X(t)，即X(t)=x(t)+w(t)。其中，w(t)的强度由标准差比Rstd(Ratio of Standard Deviation)参数决定:

式中，STD1和STD2分别是白噪声与目标信号的标准差。

(2)对进行X(t)进行EMD分解，得到各个IMF分量。

(3)重复以上两步，给目标信号第i次加入不同的白噪声wi(t)，分解后得到:

式中，imfij表示第i次加入白噪声经EMD分解后的第j个IMF分量。

(4)取相应IMF均值最为最终的IMF，例如最终的第 j个 IMF分量为，原始信号表示为:

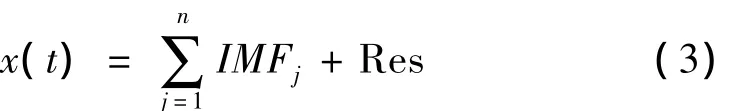
式中，N表示集合数，即添加白噪声序列的数目，Res是最终的残余项。

该方法利用高斯白噪声统计均值为零的特性，使加入白噪声后的信号具有均匀分布的分解尺度，同时也平滑了脉冲干扰等异常事件，可有效解决模态混叠问题。在步骤(1)中，相关文献［10－11］建议Rstd取值为0.1－0.4，但是添加白噪声强度量级的不准确会影响到处理效果。针对原始载荷谱信号中所含真实噪声水平未知的问题，本文提出了通过迭代准则来确定Rstd参数的求取方法。此外，步骤(3)中总体平均计算不仅可消除添加白噪声的附加影响，也可降低原始信号中的噪声影响。

1.2 EEMD的降噪步骤

通过1.1节可以发现，原始信号经过EEMD层层“筛分”得到从高频到低频有序排列IMF分量，即EEMD本质上是一个从高频到低频不断滤波的过程。进行室内道路模拟试验之前，载荷谱前期滤波方法使用的是Fourier低通或带通滤波法，是在频域内进行的，而EMD和EEMD滤波法是在时域内进行的，避免状态域的转换而丢失相关重要信息。载荷谱分解后得到的前若干阶高频IMF通常情况下为干扰噪声，而其中最低频的IMF为残余项。EEMD的降噪过程，即通过删除前若干阶IMF及残余项，将剩余IMF进行重新构造，从而实现道路载荷谱降噪的目的。EEMD整个降噪流程见图1所示。

图1 EEMD降噪流程Fig.1 Denoising process based on EEMD

2 基于EEMD的道路载荷谱降噪处理

本节内容是以某型号自卸车在不整齐石块路上的实测载荷谱为研究对象，与EMD降噪效果分别在时域、频域和雨流域进行了比较，并探讨了EEMD在不同计算参数下的降噪效果，并为后期室内道路模拟试验奠定了一定基础。

图2 道路载荷谱采集现场Fig.2 Road load spectra acpuisition site

图3 前轴右轴头原始道路载荷谱Fig.3 Original signal of front－axle right axis head

2.1 EEMD的标准差比参数确定

步骤2 相关计算:将得到的前2阶IMF分量以及二者之和作为广义应力信号，分别使用雨流计数法统计载荷循环数，并按照预先给定的标准S－N曲线，根据Miner法则估算伪累积损伤值。

步骤3 判别条件:如果循环统计次数与伪累积损伤值变化变化误差不在3%以内，那么需要重新计算新的Rstd，即用前2阶IMF分量之和的标准差除以原始载荷谱的标准差，重复以上两个步骤。如果相对误差在3%以内，即可认为当前添加的白噪声水平接近真实的噪声水平，确定最终的Rstd值。

本次原始载荷谱的EEMD标准差比Rstd迭代过程见表1。由于EEMD进行初始分解后，前2阶IMF分量之后的标准差过大，说明标准比取0.1不合理，不宜作为新的Rstd迭代，因此使用IMF1的标准差除以原始载荷谱的标准差，得到下一步的Rstd值为0.1786。经过反复迭代，确定最佳Rstd值为0.2841，则同时可以估算出原始噪声的标准差约为4.5484 m·s－2。

表1 标准方差比的迭代Tab.1 Iteration of Rstd

2.2 EMD与EEMD的分解对比

对原始载荷谱进行EMD和EEMD计算，其中EEMD的Rstd设置为0.2841，添加白噪声数目是200次。图4列出了前7阶IMF分量以及残余项Res的计算结果。

观察图4可知，EMD和EEMD分解得到的IMF分量在局部尺度上存在差别，筛分后的累积效应最终体现在残余项上，显然EMD所得残余项的幅值相对较大。由表2可知，EMD得到的IMF1与IMF2的标准差经计算分别是 3.9270 m·s－2和 10.8809 m·s－2，且EEMD的 IMF1和 IMF2的标准差分别是 1.8246 m·s－2和3.4471 m·s－2，表明 EEMD 将干扰噪声分解到两个不同尺度的IMF中，而EMD只分解到第1阶IMF中。二者分解得到的IMF3都是原始载荷谱的主要分量，只是由EMD得到的IMF3的部分真实信号成分已泄漏到IMF2里，即产生了模态混叠现象。

表2 IMF的标准差计算结果Tab.2 Stand deviation results of IMF

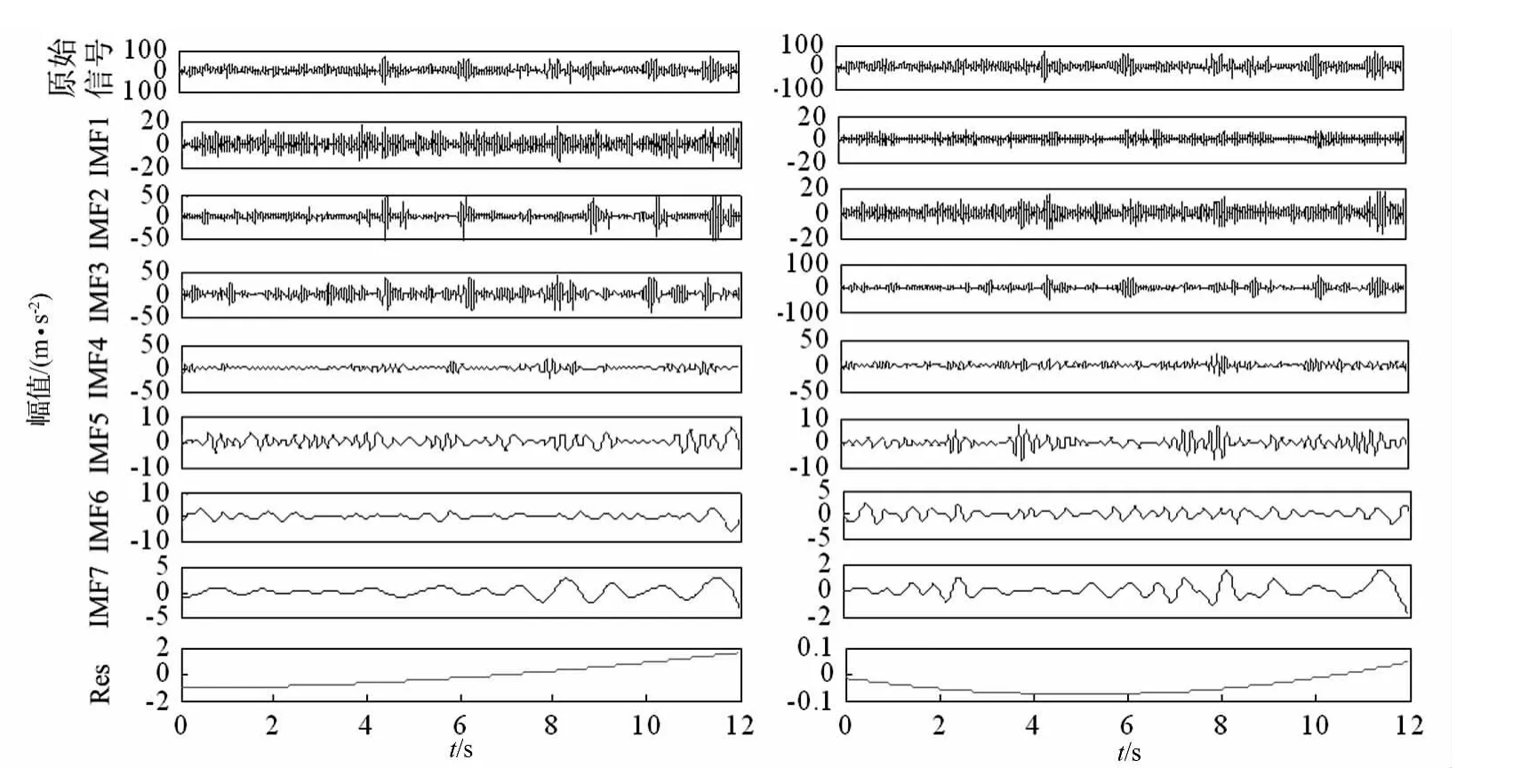
图4 EMD和EEMD的前7阶IMF和残余项Fig.4 Partial decomposition results of EMD and EEMD

2.3 降噪效果评价

2.3.1 时域波形对比

删除前若干阶IMF与残余项Res，将剩余分量进行叠加重构，生成新的道路载荷谱。图5是滤波前后的载荷谱波形对比，为观察方便，时域长度截取4－5 s区段。删除IMF1分量及Res(图5(a))，两种方法重构后的载荷谱能够保持原始载荷谱的非平稳特征，但是删除前2阶IMF分量及Res(图5(b))后，EEMD重构后的载荷谱仍然能够保持原始局部非平稳特征，为后续试验的处理提供了较为真实的载荷谱数据，而EMD得到的载荷谱已经产生明显的失真，说明EEMD提高信噪比的精度相对优于EMD。

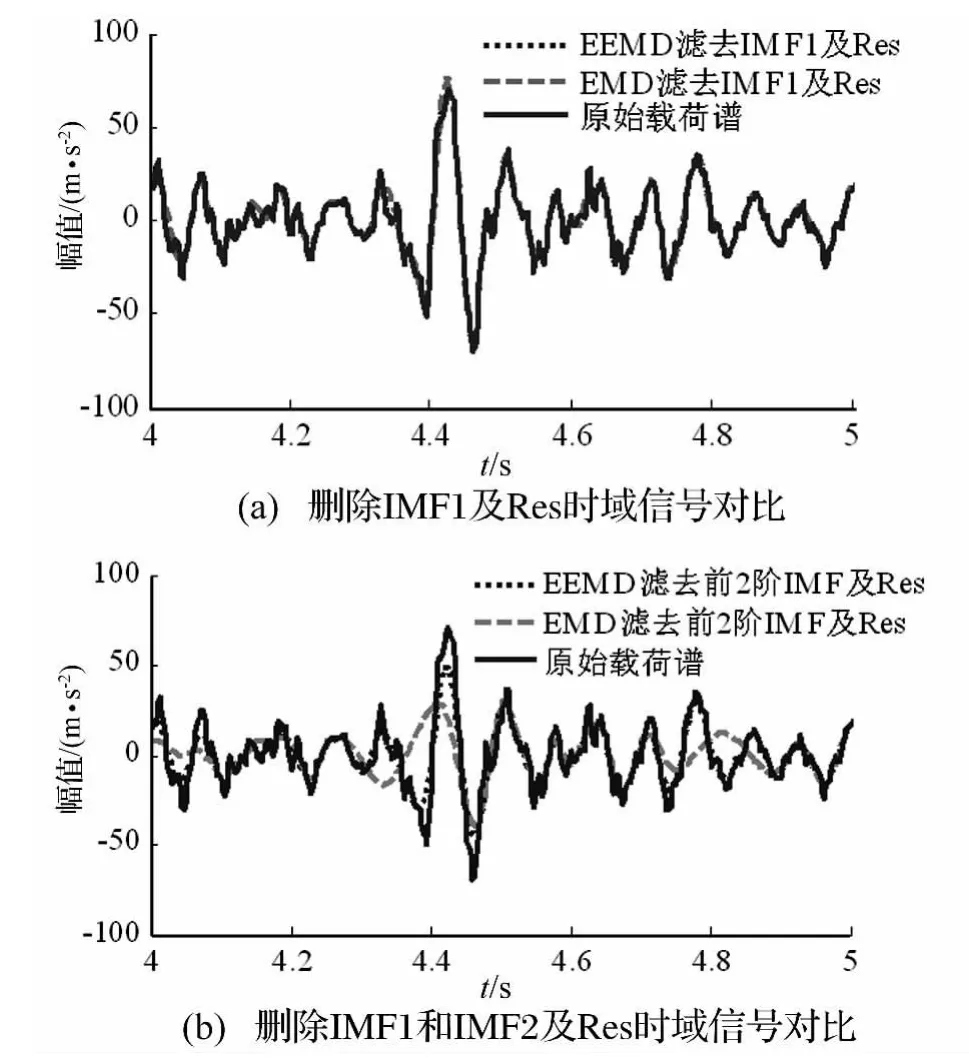
图5 重构时域波形对比Fig.5 Comparision of reconstructed signals in time domain

2.3.2 频域能量对比

Hilbert边际谱［5］是Hilbert时频谱在时间轴上的积分，表示信号在概率意义上的累积幅值(或能量)大小，反映出信号幅值(或能量)在整个(瞬时)频率段上随(瞬时)频率的变化规律。由Hilbert边际谱对比图(图6)可以看出，原始载荷谱的能量主要集中在0.5－20 Hz频带内，60 Hz以上明显存在干扰噪声，表3列出了EMD和EEMD的降噪效果。删除第1阶IMF及Res，EMD和EEMD分别滤去50 Hz以上和60 Hz以上的高频能量;删除前2阶IMF及Res，EMD和EEMD分别滤去20－50 Hz和25－60 Hz的能量。对于例如自卸车一类的重型工程车辆而言，在进行室内道路模拟试验时，一般要求滤波后的载荷谱信号在约0.5－30 Hz即可满足迭代要求，而EEMD去除前2阶IMF及Res能够满足要求。

观察PSD对比图(图7)可知(为观察方便，选取三组数据，幅值采用对数坐标形式)，删除前2阶IMF及Res，EMD和EEMD相对于原始载荷谱都保持了30 Hz以内的主要能量，30 Hz以外的高频噪声信号得到有效抑制，可作为后期室内道路模拟试验的迭代目标。

图6 Hilbert边际谱对比Fig.6 Comparision of Hilbert marginal spectrum

图7 功率谱密度函数PSD对比Fig.7 Comparision of Power Spectrum Density Function

2.3.3 雨流域损伤对比

室内道路模拟试验的关键步骤之一就是各强化道路段组合系数的获取，而最优化组合系数的计算依赖于伪损伤值的计算。伪损伤值一般通过雨流计数法求得。然而干扰噪声的存在，使得雨流法统计时会产生虚假的应力循环，显著降低疲损伤估计的精度，并且目前室内道路模拟试验依据的是远程参数控制(Remote Parameter Control，RPC)技术，要求目标道路载荷谱具有很高的信噪比，但是噪声会严重影响室内道路模拟试验中影响迭代的次数和精度。

循环次数是评价疲劳寿命的一个重要指标，图8是载荷谱消噪前后的雨流循环统计结果。观察图8可知，重构之后的载荷谱，主要被滤去了均值较大、幅值较小的疲劳循环，并且缩减了部分均值较小的疲劳循环累积频次。为方便计算结果的对比，通过预先设定的S－N曲线，将各载荷谱名义疲劳累积损伤值作归一化处理(以原始载荷谱的损伤值为基准，其名义疲劳累积损伤值为1，即预设材料在原始载荷状态下达到极限寿命)，结果见表3。可见噪声对疲劳损伤的计算有很大影响，如不作降噪处理会导致强化道路组合的优化结果存在误差。基于EEMD方法的降噪处理能够保留真实的疲劳循环次数。

图8 雨流计算结果对比图Fig.8 Comparision of rainflow calculation results

表3 EMD与EEMD降噪后的循环次数与伪损伤Tab.3 Calculation of cycle number and pseudo-damage after denoising based on EMD and EEMD

3 EEMD计算参数对降噪效果的影响

EEMD降噪算法主要依赖于两大计算参数，即Rstd与加入白噪声的数目N，并且对分析信号的影响服从下式的统计规律［9］:

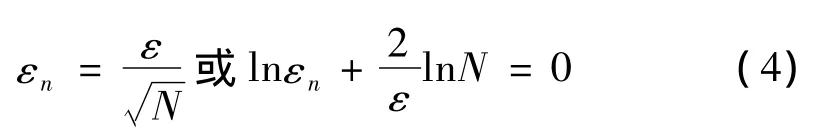
式(4)中，ε是白噪声强度(由Rstd参数决定)，εn是原始信号与最终IMF重构信号之间的误差。式(4)表明白噪声强度与分解结果的精度成反比。为了在分解精度和计算量之间取得折衷，要求确定合适的白噪声强度和集合数N。本文在2.1节已提出Rstd参数合适的选择方法，为了研究两参数对EEMD计算结果的具体影响情况，将原始载荷谱分解完成后均删除前2阶IMF分量及残余项，计算结果如表4所示。表4说明，若添加白噪声的强度太小，则无法影响到EMD运算中极点的选取，进而失去补充尺度的作用，从而不能很好地解决模态混叠问题;反之，若所加入的噪声强度太大，反而形成二次噪声污染。为保证分解误差满足精度要求，集合数必须选取的较大，然而随着集合数的增加，计算时间亦明显增加。显然，EEMD计算时加入噪声的强度越接近于实际噪声的强度，统计循环次数值越稳定，表明降噪效果越好。

表4 EEMD计算参数对降噪效果的影响Tab.4 Effects of the EEMD computational parameters on denoising

4 结论

综合本文，主要有以下三点结论:

(1)EEMD克服了EMD的固有缺陷，不用选择基函数且具有自适应性，分解出的IMF分量具有实际的物理意义。该方法更为方便、灵活，可应用于室内道路模拟试验道路载荷谱的降噪处理中。

(2)EEMD计算参数Rstd能通过有限次的迭代试验求得，同时可估算出原始噪声水平，而集合数N在保证计算精度前提下可适当减小，以节省计算时间，提高计算效率。

(3)通过与EMD在时域、频域、雨流域的对比，表明运用EEMD降噪后可以保持原始道路载荷谱的主要能量，同时提高道路载荷谱的信噪比和应力循环次数统计的精度，为进行后期室内道路模拟试验奠定了一定基础。该方法实际应用于某自卸车道路模拟试验，对确定滤波频率范围以及迭代信号预处理起到较好的辅助作用。

针对EEMD方法的降噪优势，将其引入作为道路载荷谱前期分析及处理工具，为载荷谱的降噪处理提供了新思路。

［1］宋勤，姜丁，赵晓鹏，等.道路模拟试验载荷谱的采集、处理与应用［J］.仪表技术与传感器，2011，3:104 －106.SONG Qin， JIANG Ding， ZHAO Xiao－peng，et al.Acquisition，processing and application of load spectrum for road simulation test［J］.Instrument Technique and Sensor，2011，3:104 －106.

［2］陈隽，李想.运用总体经验模态分解的疲劳信号降噪方法［J］.振动、测试与诊断，2011，31(1):15 －19.CHEN Jun，LI Xiang.Application of ensemble empirical mode decomposition to noise reduction of fatigue signal［J］.Journal of Vibration，Measurement＆ Diagnosis，2011，31(1):15－19.

［3］钱立军，吴道俊，杨年炯，等.基于室内道路模拟技术的整车加速耐久性试验的研究［J］.汽车工程，2011，33(2):91－96.QIAN Li－jun，WU Dao－jun，YANG Nian－jiong，et al.A research on vehicle accelerated durability test based on indoor road simulation tchnology ［J］.Automotive Engineering，2011，33(2):91－96.

［4］陈淑萍，程磊.基于Hilbert－Huang变换理论的非线性系统分析［J］.系统工程与电子技术，2008，30(4):719 －722.CHEN Shu－ping，CHENG Lei.Nonlinear system analysis based on Hilbert－Huang transform theory ［J］.Systems Engineering and Electronics，2008，30(4):719 －722.

［5］Huang N E，Shen Z，Long R S.et al.The empirical mode decomposition and Hilbert spectrum for nonlinear and nonstationary time series analysis［C］.Proceedings of the Royal Society of London A，1998，454:903 －995.

［6］Wu Z H，Huang N E.A study of the characteristics of white noise using the empirical mode decomposition method［J］.Proceedings the Royalof Society A，2004，460:1597－1611.

［7］Wu Z H， Huang N E. Ensemble empirical mode decomposition:a noise－assisted data analysis method ［J］.Advances in Adaptive Data Analysis，2009，1(1):1－41.

［8］吕建新，吴虎胜，田杰.EEMD的非平稳信号降噪及其故障诊断应用［J］.计算机工程与应用，2011，47(28):223－227.LÜ Jian－xin，WU Hu－sheng，TIAN Jie.Signal denoising based on EEMD for non－stationary signals and its application in fault diagnosis ［J］.Computer Engineering and Applications，2011，47(28):223－227.

［9］陈文驰，刘飞.一种基于EEMD的过程数据混合去噪方法［J］.计算机应用研究，2012，29(4):1368 －1370.CHEN Wen－chi，LIU Fei.Hybrid process data denoising method based on EEMD ［J］.Application Research of Computers，2012，29(4):1368 －1370.

［10］曹冲锋，杨世锡，杨将新.大型旋转机械非平稳振动信号的EEMD 降噪方法［J］.振动与冲击，2009，28(9):33－37.CAO Chong－feng， YANG Shi－xi， YANG Jiang－xin. Denoising method for non－stationary vibration signals of large rotating machineries based on ensemble empirical mode decomposition［J］.Journal of Vibration and Shock，2009，28(9):33－37.

［11］焦彦军，胡春.基于改进EEMD方法的数字滤波器［J］.电力自动化设备，2011，31(11):64 －68.

JIAO Yan－jun，HU Chun.Digital filter based on improved EEMD method ［J］.Electric Power Automation Equipment，2011，31(11):64 －68.

［12］Huang N E，Wu M L，Long S R，et al.A confidence limit for the empirical mode decomposition and Hilbert spectral analysis［J］.Proceeding of Royal Society London A，2003，459:

2317－2345.