An experimental study of impact loading on deck of shore-connecting jetties exposed to oblique waves and current*

MENG Yan-qiu (孟艳秋), CHEN Guo-ping (陈国平)

Key Laboratory of Coastal Disaster and Defence, Ministry of Education, Hohai University, Nanjing 210098, China, E-mail: yqmeng@126.com

YAN Shi-chang (严士常)

College of Harbour, Coastal and Offshore Engineering, Hohai University, Nanjing 210098, China

TONG Chao-feng (童朝锋)

State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Hohai University Nanjing 210098, China

An experimental study of impact loading on deck of shore-connecting jetties exposed to oblique waves and current*

MENG Yan-qiu (孟艳秋), CHEN Guo-ping (陈国平)

Key Laboratory of Coastal Disaster and Defence, Ministry of Education, Hohai University, Nanjing 210098, China, E-mail: yqmeng@126.com

YAN Shi-chang (严士常)

College of Harbour, Coastal and Offshore Engineering, Hohai University, Nanjing 210098, China

TONG Chao-feng (童朝锋)

State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Hohai University Nanjing 210098, China

(Received December 3, 2012, Revised May 8, 2013)

The impact pressure from waves is an important issue to be considered in the design of coastal structures. In this paper, the waves acting on the deck of a shore-connecting jetty on a slope exposed to oblique waves and in the presence of current are examined based on laboratory experiments. The impact pressures are measured on a 1:50 scale model of a jetty head with down-standing beams and berthing members. The relations of the impact pressure with the incident wave angle and the current velocity are examined. It is shown that the impact pressure is sensitive to the wave angle and the current velocity. A computational model for the impact load on the deck of shore-connecting jetties exposed to oblique waves and current is developed.

wave, current, impact pressure, shore-connecting jetty on a slope

Introduction

Recently, in a number of ocean structures like jetties, bridges and coastal platforms extensive deck damages were found under a large wave action. It is shown that the wave-in-deck uplift loads are very critical in the overall design of the superstructures in storm-prone areas (44 highway bridges were destroyed by Hurricane Katrina[1]). In most cases, the damage is caused by high impact pressures and loads when large wave crests slam onto the deck due to the improper selection of the deck elevation. Therefore, it is necessary to assess the typical environmental forces at the location before the design of such structures. The accurate prediction of the wave slamming force on the deck of ocean structures is of importance in the structural design.

The pure wave slamming on superstructures of jetties and similar ocean structures was well studied. In some investigations, based on momentum and energy considerations, the forces were typically modeled as the rate of change of the momentum of the water due to the waves hitting the element. Physical model tests were carried out to investigate the vertical wave load on the deck of jetties and prediction models were proposed for design purposes[2-11]. Their main findings regarding the vertical wave load are that the load is affected by the clearance of the deck (the vertical distance between the deck and the still water level) and can be expressed as a function of the deck clearance.

These studies are based on model tests in the wave field only. However, coastal structures are often exposed to combined wind, wave and current actions. When the waves propagate toward a structure in a current field, the wave properties, the diffraction pattern and the resultant loading on the ocean structures canbe significantly different from the wave-only case. Assessing the behavior of coastal structures under the wave-current action is of importance for design.

Fig.1 Experiment setup

The wave-current interactions were studied in various cases. Based on the principle of conservation of the wave action flux, Li and Teng[12]investigated the wave transformations during oblique waves travelling in a steady uniform current, with the angle between the wave and the current in the range ofoo5＜α＜85 and 95o＜α＜175o. Variations of the wave height will influence the wave impact on the ocean structure. The wave-current forces on ocean structures could be classified into two categories, the wave and current actions on structures of small size (such as piles and other cylinder-like structure) and those on structures of large size (for example, jetties, bridges and platforms). For a large ocean structure, such as a jetty and a platform, numerical models were proposed based on the perturbation-based potential theory in the frequency domain[13]. Numerical solutions were obtained based on directly solving the problem in the time domain[14,15].

However, the wave-current induced slamming load onto the deck of jetties is not well studied. In this paper, the impact pressure on the deck under oblique waves and in steady uniform current is examined based on laboratory experiments. The relations of the impact force with the incident wave angle and the current velocity are analyzed.

Fig.2 The layout of pressure transducers and force transducers on the test deck model

Fig.3 Sketch of test conditions

1. Experimental setup

The wave tests were conducted in a wave tank of 50 m long, 17.5 m wide and 1.5 m deep at Nanjing Hydraulic Research Institute, China. Irregular waves were generated by a wave maker at one end of the tank. In order to mitigate the wave reflection on the boundaries, a mild slope was laid at the other end of the tank and wave absorbers were installed on the twosides of the tank. Pumps were arranged in the wave tank to generate steady currents of different velocities in various directions inducted by the current inducting wall, as shown in Fig.1(a).

The test model was designed as an undistorted model with scale of 1:50 to the prototype structure jetty of Harbor Beilun according to the Froude law. In order to make the environmental conditions around the test section more close to the real field and keep the test section from the influence of waves and currents at the two ends of the jetty model, the length of the model was selected to be 10 m and a part of 0.32 m long in the middle was used as the test section. The organic glass model is of 1.116 m wide with two kind of berthing members in front of the model jetty head, as shown in Fig.1(b). Four force transducers and ten pressure gauges were fitted on the deck, the rest three pressure gauges were fitted on the down-standing longitudinal beams. Load measurements were recorded at a sampling frequency of 125 Hz. The duration for each wave set was 5 min-9 min and the wave number was 120. Each group of tests was repeated 3 times so that the reliability of the measured data could be guaranteed. The average value was finally adopted.

The water depth at the jetty model was d=0.4 m. The slope of the bottom in the test was 1:2. The tests covered a range of wave conditions (JONSWAP Spectra γ=3.3, the model scale: the significant incident wave height Hs=0.045 m, 0.065 m, 0.085 m, the mean incident wave period Tm=1.0 s, 1.38 s, 1.54 s, the prototype scale: the significant incident wave height Hs_f=2.25 m, 3.25 m, 4.25 m, the mean incident wave period Ts_f=7.071 s, 9.758 s, 10.899 s ). The wave incident angles were β=0o, 15o, 30o, 45o, 60o. The angle between the wave and the current α was used to distinguish two conditions, the oblique wave propagating in a following currento(90) α＜and the oblique wave propagating in an opposing current (α＞90o). For the above two angles, the relationship β=is held. The angle 90o-α less than zero denotes the cases that the oblique waves travel against the current. The current velocities (model scale) selected were U=0 m/s , 0.14 m/s, 0.21 m/s, 0.28 m/s, 0.35 m/s. Four different clearances (model scale) Δh were tested: Δh=0.025 m, 0.055 m, 0.075 m, 0.115 m, achieved by raising the deck. The experimental setup and a sketch of the tested configuration are shown in Figs.1-3.

The wave incident angle β (the angle between the wave propagation direction and the normal line of the jetty) was changed by turning the model. Seven cases were tested: Case 1: the wave normal to the deck without current, Case 2: the wave oblique to the deck without current, Case 3: the wave normal to the deck with following currents, Case 4: the wave normal to the deck with opposing currents, Case 5: the wave normal to the deck with currents perpendicular to the wave, Case 6: the wave oblique to the deck with following currents, Case 7: the wave oblique to the deck with opposing currents, as shown in Fig.3.

The velocity of the steady uniform current in tests was controlled by the pumps, the direction was determined through the inducting wall, as shown in Fig.1(b). The current was generated in advance, the wave was generated after the velocity and the direction of the current at the test section became steady.

2. Results and discussions

The recorded impact pressure data from experiments are analyzed. The maximum pressure of the total 13 pressure measurements (the statistical pressure p1/3is applied here) is used.

Fig.4 Variation of K1with the wave incident angle β

2.1 Effect of the wave incident angle on the impact pressure

The factor K1is plotted against the wave incident angle β in Fig.4. Here we define the factor K1= pβ,0/p0,0, as the ratio of the impact pressure pβ,0induced by the oblique wave with the incident angle β to the impact pressure p0,0obtained from the normal incident wave, without current. Although there are some scatters in Fig.5, we still can see an influence of increasing incident angle β on decreasing K1, particularly whenoo0＜β＜45, which indicates that thenormal wave gives the maximum impact pressure. The impact pressure decreases by about 60% at β= 60owith respect to that under the normal wave attack (β=0o). This reduction can be attributed to the fact that the component of the wave perpendicular to the structure reduces under the oblique attack. Due to the random behaviour of the wave impact pressure on the deck of shore-connecting jetties, there are some scatters in the data sets. Figure 4 shows all available data points pertaining to different wave conditions and deck clearances. When all effects are incorporated into one figure, some scatters can be shown. It is noted that not enough data are available to give a satisfactory explanation for the scatters.

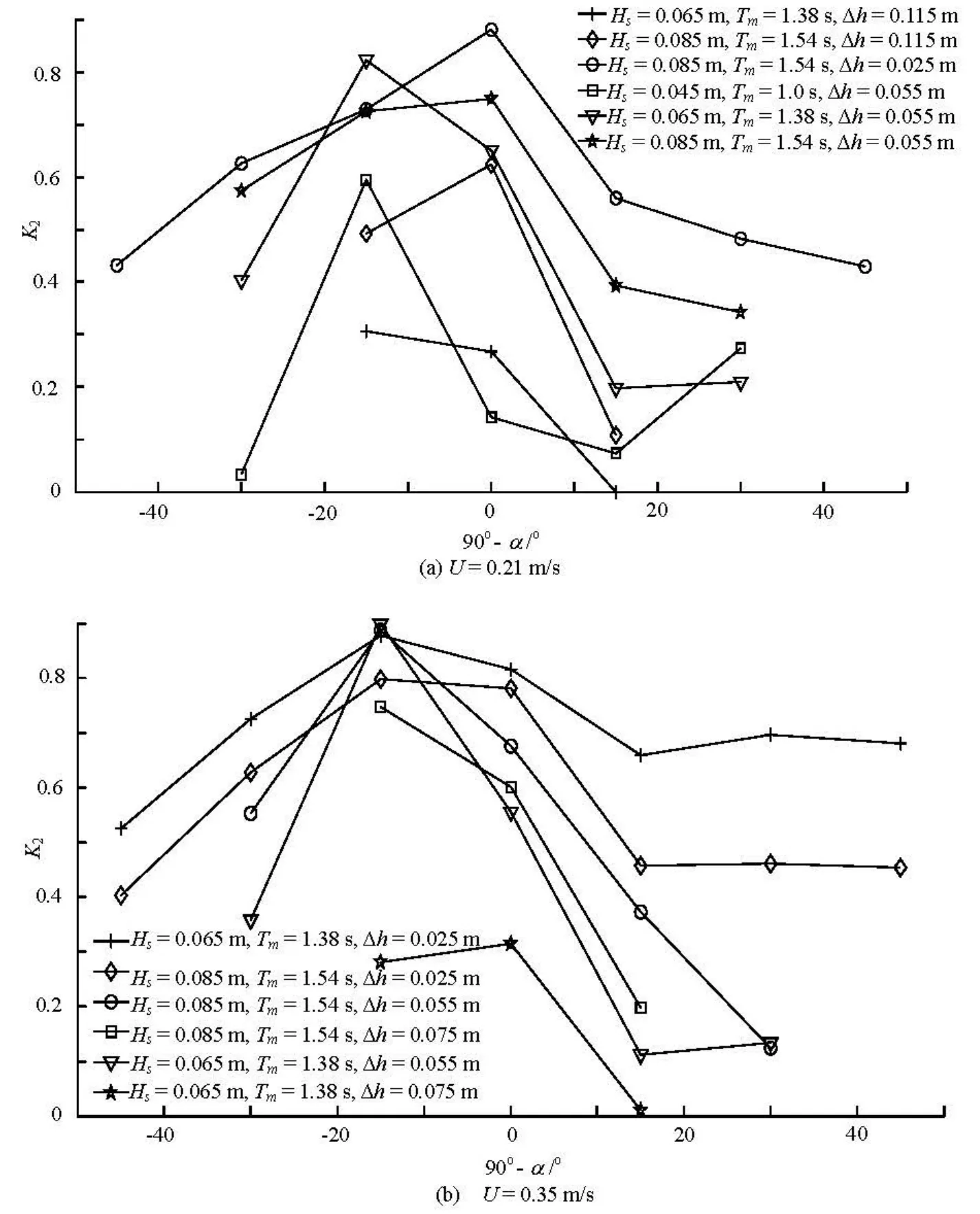
Fig.5 Variation of K2with the angleo90-α at given current velocity

2.2 Combined effect of oblique wave and current on the impact pressure

Figure 5 shows the variation of the factor K2against the angle 90o-α, for a fixed current magnitude U =0.21m/s and U =0.35 m/s .

The factor K2=p90o-α,U/p0o ,0is used to reveal the combined effect of the current and the oblique wave on the impact pressure, where p0o ,0denotes the impact pressure from the wave normal to the deck, without current, p90o -α,Uis the impact pressure of the oblique wave traveling at an angle α to the direction of the current. From these figures, although there are some scatters, it can still seen that, (1) with waves propagating on a favorable current (90o＜90o-α＜90o), the values of K decrease rapidly with the in-

2crease of 90o-α from 0oto 15o, then the values slightly decrease as 90o-α increases from 15oto 45o, as shown in Fig.5, (2) with wave propagating onan adverse current (-90°＜90°-α＜0°), the values of K2increase as 90o-α decreases from-15o, then decrease as 90o-α decreases from -15oto -45o, as shown in Fig.5.

The influence of the current on the wave impact pressure is not so straightforward. It might be interpreted as follows: when a wave encounters a uniform current, they interact with it, so that the wave height changes in the wave-current field. Zhou et al.[2]shows that, for a fixed clearance, the wave impact pressure on the deck is related to the wave height. As a result, the wave impact is significantly affected by the current.

Li[12]investigated the wave transformations for the case with a current flowing at an angle to the direction of the wave propagation. He shows that the wave refraction has a more complicated behavior, which can be described as follows: when the waves travel with a current, the refracted wave height initially decreases up to the angleoo90-α=30, outside of this range the refraction effect due to the current becomes pronounced, which makes the refracted wave height increase with the increase ofo90-α, and with the increase of the current velocity, the effects become more evident. Based on the above analysis of the wave height variations, it can be concluded that the changes of the impact pressures follow similar trends, though there are some slight inconsistencies. It should be noted that the impact pressure variation is related not only to the wave refraction through a current, but also to the oblique incident wave attack. In the present tests, the transitional phenomenon takes place at 90o-α=15o, which could be attributed to the combined effect of the wave and the current. From the above analysis, for 90o-α larger than 15o, the effect of the oblique incident wave results in a decrease of the impact pressure with the increase of the incident wave angle(β=), while the refraction effect may lead to an increase of the impact pressure with the increase of 90o-α. The effect of the oblique incident wave is found to be more dominant in the range of 15o＜90o-α＜30o. The resulting pattern is that in the range of 15o＜90o-α＜30o, K2decreases fairly slowly with the increase of 90o-α, wheareas, when 90o-α is larger than 30o, K slightly increases with

2the increase of 90o-α.

Li[12]also shows that for the case when the current is in the opposite direction, an opposite trend can be detected. The refracted wave height increases with the increasing angle up to=15o. With a further increase of the angle, a decrease of the refracted wave height values would be resulted. The same influence is found for the impact pressure, as shown in Fig.5.

Fig.6 Variation of K3with the relative current velocity U/ C when wave propagates in a favorable current

Fig.7 Variation of K3with the relative current velocity U/ C when wave propagates in an adverse current

2.3 Effect of the current velocity on the impact pressure

Figures 6, 7, respectively, show the variation of the factor K3due to the varying relative current velocity U/ C (the ratio between the current velocity U and the wave celerity C) for differento90-α. Five current velocities are considered: U=0 m/s , U= 0.14 m/s, U =0.21m/s , U =0.28 m/s , and U= 0.35 m/s. The celerity velocity can be expressed by the following equation:C=(g/ k)tanh(kd), where the wave number k=2π/L, d is the water depth, and L is the wave lengh for T=Tm. Three different wave celerities in the model scale are used: C= 1.4625 m/s, 1.7 m/s, 1.755 m/s. The factor K3= pβ,U/pβ,0reflectes the influence of the current speed, where pβ,Udenotes the impact pressure from the oblique wave (with incident angle β) along with currents, pβ,0denotes the impact pressure induced by the same wave without currents. Figure 6 shows that for the waves travelling with the current (90o-α＞0o), the variations of K3with the relative current velocity have differnt trends for differnto90-α. The factor K3decreases with the increasing presence of the current for 90o-α=15o. When 90o-α=30o, as the current is strengthened, the descent of K3slows down, and in some cases K3goes up at a large relative current velocity. A significant increase of K3occurs whenoo

90-α=45.

The results of changes of K3for waves propagating in an adverse current are shown in Fig.7. The factor K3is shown increasing with the increasing current velocity for 90o-α=-15o. When 90o-α=-30o, as the current is strengthened, the increase of K3is insignificant with respect to the scatters of the data. As 90o-α is equal to -45o, the increase of K3slows down and furthur K3goes decreasing.

The observations mentioned above are due to the intense refraction of the oblique wave in the current, which has a great influnence on the wave height and hence affects the impact pressure.

3. Predictions

With the information from the previous sections, a multiple regression analysis is carried out on the data sets. First the influence of the incident wave angle β on K is checked. The combination of a cosine function and a power function is fitted through the data points in Fig.4. The tests with varying incident wave angles are used to determine the power index and the coefficient. The influences of the current velocity and the angle between the wave and the currenthave to be taken into account. From Figs.5 to 7, it is shown that K is dependent on the relative current velocity U/ C and the angleo90-α. The above observation leads to the following assumption: the assumed hyperbolic tangent functions describing the relation of K with the relative current velocity U/ C and the angleo90-α are used to fit the data from experiments. A non-linear regression is applied to the data, using the least squares method. Some of the coefficient values in Eq.(1) are not the results directly obtained by the regression analysis, they are based on the results of a manual fitting to the plotted data. An adjustment is made to yield a smooth variation of the coefficient values with respect to the relative deck clearance Δh/ Hs. When large scatters are present, an average trend might be drawn by using the regression method. However, for a design or safety assessment of the structure, it is advisable not to follow the average trend, but to include an uncertainty margin of the prediction. In this study, we apply the upper envelope to the random wave test results. Eventually, Eq.(1) for prediction is obtained as

Fig.8 Comparison of the measured and predicted factors K

This computation procedure is to solve the actualdesign problems of the wave impact on the deck of shore-connecting jetties exposed to oblique waves and current. Comparisons between the measured and the predicted results are made to evaluate its validity. It can be seen from Fig.8 that the prediction formula of Eq.(1) approximately represents the upper envelope of the random wave test results. The agreement between the formula and the laboratory data is therefore not perfect. A reason for this can be that the relative deck clearance Δh/ Hshas some influence on the value of K, however, it is not clear what the exact influence is .This derived formula is a simple method to correct the results from head-on wave attacks without current presence for an oblique wave attack with current presence. In the computation method for calculating the impact pressure on the deck from head-on waves without current presence, the influence of the relative deck clearance has been taken into account[12]. In engineering practice, the difference between the measured and the predicted correction factor K may be disregarded for one needs simple and quick design methods. So we simplify the relevant processes and propose a conservative assumption of a formula about the correction factor K.

Equation (1) is useful and can be recommended when assessing the wave impact pressure for Δh/ Hsin the range of around 0.3-0.4 (note that the scatter around the prediction is significantly reduced in this range) and the wave impact on the deck of a shoreconnecting jetty exposed to oblique waves and currents for which limited information is available in literature. From the practicing engineers’ viewpoint, it is suggested to effectively employ the prediction formulas for a preliminary design only. Further investigations through hydraulic model tests are necessary for achieving more reliable information.

The best way to deal with the impact pressure is to include a design prevention of dangerous conditions by estimating the impact pressure on the deck. The deck must have its clearance optimized. In the design of a deck against the wave impact pressure, one should be very careful. If the deck must be designed to have a dangerous deck clearance, measures should be taken to resist such impact pressures.

4. Conclusions

In this study, model tests were conducted to investigate the impact pressure on the deck of a shore-connecting jetty on a slope of oblique waves with the presence of a current.

The following conclusions can be drawn from the experimental results:

(1) The impact pressure depends significantly on the wave angles. It is shown that the maximum pressure occurs at the normal wave incidence.

(2) With waves propagating in a favorable current (0o＜90o-α＜90o), the impact pressure decreases rapidly as 90o-α increases from 0oto 15o, then the values slightly decrease as 90o-α increases from 15oto 45o. With waves propagating in an adverse current (-90o＜90o-α＜0o), the values of K2increase as 90o-α decreases from 0oto -15o, then K2decreases as 90o-α decreases from -15oto -45o.

(3) Changing the current velocity affects the wave impact pressure. With the increase of the current velocity, the effects become more evident.

(4) An empirical formula is established for the calculation of the correction factor, which is used to correct the wave impact pressure on the deck from head-on waves attack without current presence for an oblique wave attack with current presence.

[1] CHEN Q., WANG L. and ZHAO H. Hydrodynamic investigation of coastal bridge collapse during Hurricane Katrina[J].Journal of Hydraulic Engineering,ASCE,2009, 135(3): 175-186.

[2] ZHOU Yi-ren, CHEN Guo-ping and HUANG Hai-long et al. Uplift pressure of waves on a horizontal plate[J].China Ocean Engineering,2003, 17(3): 355-368.

[3] ZHOU Yi-ren, CHEN Guo-ping and HUANG Hai-long et al. Experimental study on uplift forces of waves on a horizontal plate of wharf on a slope[J].Journal of Hydrodynamics, Ser. A,2004, 19(5): 687-694(in Chinese).

[4] ZHOU Yi-ren, CHEN Guo-ping and WANG Deng-ting. Calculation methods of uplift forces of waves on a horizontal plate of wharf on a slope[J].Journal of Hydro-dynamics, Ser. A,2005, 19(5): 73-78(in Chinese).

[5] REN B., WANG Y. Laboratory study of random wave slamming on a piled wharf with different shore connecting structures[J].Coastal Engineering,2005, 52(5): 463-471.

[6] REN B., WANG Y. Experimental study of irregular wave impact on structures in the splash zone[J].OceanEngineering,2003, 30(18): 2363-2377.

[7] MENG Yan-qiu, Chen Guo-ping and YAN Shi-chang. Wave-in-deck uplift force on detached high-piled wharf[J].Journal of PLA University of Science and Technology (Natural Science Edition),2010, 11(1): 72-78(in Chinese).

[8] SERINALDI F., CUOMO G. Characterizing impulsive wave-in-deck loads on coastal bridges by probabilistic models of impact maxima and rise times[J].CoastalEngineering,2011, 58(9): 908-926.

[9] CUOMO G., TIRINDELLI M. and ALLSOP W. Wavein-deck loads on exposed jetties[J].Coastal Egineen-ring,2007, 54(9): 657-679.

[10] CUOMO G., SHIMOSAKO, K. I. and TAKAHASHI S. Wave-in-deck loads on coastal bridges and the role of air[J].Coastal Engineering,2009, 56(8): 793-809.

[11] CHEN Guo-ping, MENG Yan-qiu and YAN Shi-chang. Experimental investigation of irregular wave upliftforce on deck of exposed high-pile jetties[J].ChinaOcean Engineering,2010, 24(1): 67-78..

[12] LI Yu-cheng. TENG Bin.Wave-current interaction in wave action on maritime structure[M]. Beijing, China: China Ocean Press, 2002(in Chinese).

[13] JIN J., MENG B. Computation of wave loads on the superstructures of coastal highway bridges[J].Ocean Engineering,2011, 38(17): 2185-2200.

[14] SKOURUP J., CHEUNG K. F. and BINGHAM H. B. et al. Loads on a 3D body due to second-order waves and a current[J].Ocean Engineering,2000, 27(7): 707-727.

[15] WANG Yong-xue, REN Xiao-zhong and DONG Ping et al. Three-dimensional numerical simulation of wave interaction with perforated quasi-ellipse caisson[J].Water Science and Engineering,2011, 4(1): 46-60.

10.1016/S1001-6058(14)60024-X

* Project supported by the Fundamental Research Funds for the Central Universities (Grant No. 2009B10614), the National Key Techonology Research and Development Program (Grant No. 2012BAB03B00), the National Natural Science Foundation of China (Grant No. 51339005).

Biography: MENG Yan-qiu (1974-), Female, Ph. D., Lecturer