双目显微系统光路偏转与平行性检测
2014-06-01张齐元张中华刘文滨聂英华吴泉英
徐 鹍,韩 森,张齐元,谢 翔,张中华,刘文滨,聂英华,吴泉英
(1.苏州慧利仪器有限责任公司,江苏 苏州215123;2.苏州科技学院,江苏 苏州215000;3.上海理工大学,上海200093;4.六六视觉科技股份有限公司,江苏 苏州215000;5.黑龙江省计量检定测试院,黑龙江 哈尔滨150036)
引言
随着现代科学之高速发展,双目系统已经渗透到各个学科领域,从显微镜、望远镜到机器视觉、人工智能,高性能复杂结构双目系统层出不穷,这同时也给系统检测提出了新的挑战。如何高效地检测系统,评估其整体性能的优略,在研发和生产中起着至关重要的作用。好的检测方法在检测出性能指标的同时,还可以通过对检测结果的分析,逆向优化双目系统的设计和装配[1],找到提高系统性能的突破口。现今的双目系统光学检测方法按检测光束宽度可以分为宽光束检测和细光束检测。宽光束检测主要是检测系统的波像差及光学元件的面形误差[2-3],测试精度高,信息量大,内容丰富全面,可以反映大空间尺度内系统的综合属性。但其检测仪器价格比较昂贵,检测过程较复杂,而且不易找到系统病症之部位。细光束检测主要是检测系统的光路特性。文中通过使激光束从待测系统的入射端入射,观测研究反射光线和出射光线的位置和方向,检测了待测系统的光路偏转和平行性,分析了造成光路偏转和不平行的原因。
1 系统组成
待测双目系统如图1所示,文中主要检测了虚线框中的部分系统。其中各字母不仅仅表示光学元件,而是代表由光学元件和其机械结构组成的整体元件。
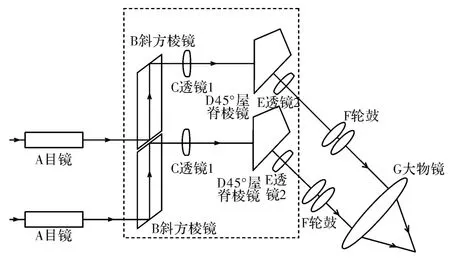
图1 待测系统组成示意图Fig.1 Schematic diagram of system under test
2 检测方法
2.1 总体检测方案
将待测双目系统拆分成元件,先检测各元件,然后逐步组合元件,由简单到复杂,由部分到整体,层层检测光路偏转和平行性。
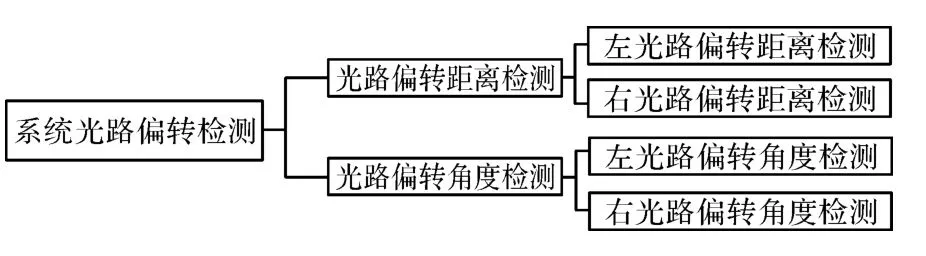
2.2 系统光路偏转检测方法
图2所示为激光束从待测系统入射端面中心O1垂直入射,理想情况下光束应从出射端面中心O2垂直射出,但实际情况光束会从O3射出,O3与O2点间的距离为d,实际出射光线O3P3和理想出射光线O2P2的夹角为θ,定义d为光路偏转距离,θ为光路偏转角度,文中采用测量d和θ的方法来检测光路偏转。
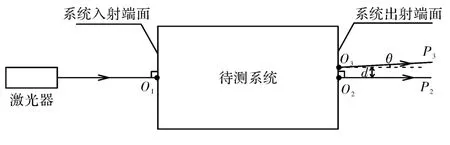
图2 光路偏转检测原理图Fig.2 Principle diagram of optical path deflection measurement
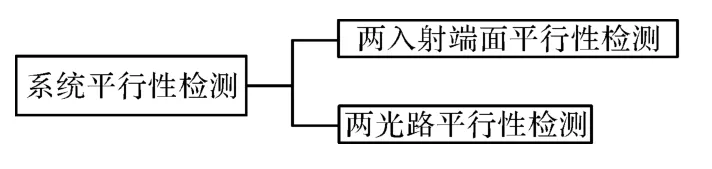
2.3 系统平行性检测方法
两入射端面平行性检测。如图3所示,理想系统两光路入射端面平行,实际系统由于安装误差,两入射端面将存在一夹角φ,文中采用测量角φ的方法来检测两入射端面平行性。
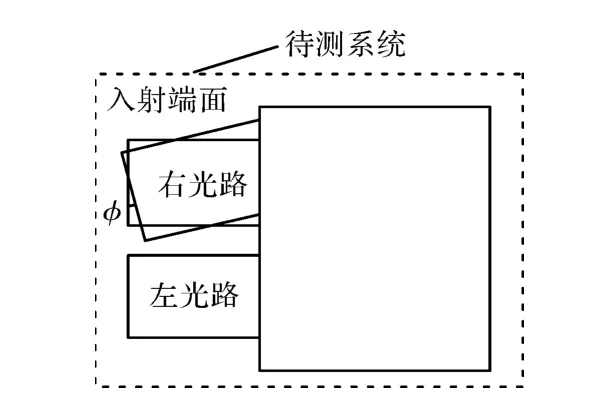
图3 系统入射端面夹角示意图Fig.3 Schematic of angle between incident faces of system
两光路平行性检测。理想双目系统两光路完全对称,2束平行光分别从左右光路入射端面中心垂直入射,光束出射后仍然平行。实际系统2束光出射后成一夹角α,文中采用测量角α的方法来检测两光路平行性,如图4所示。
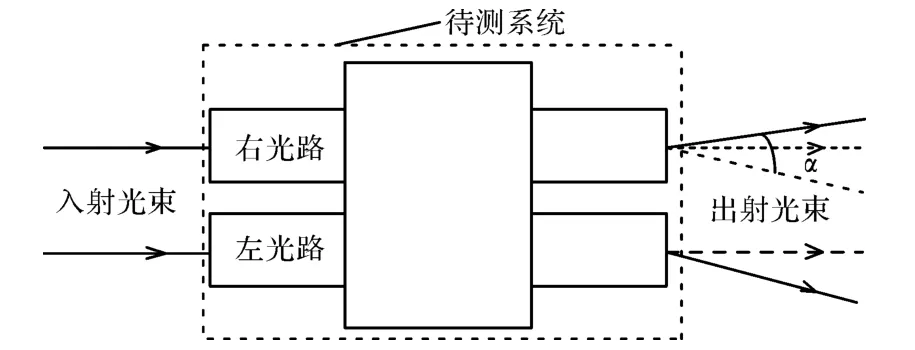
图4 两光路出射光线平行性测量原理图Fig.4 Principle diagram of emergent light parallelism detection of double-light paths
3 实验装置和检测结果
3.1 光路中心点基准建立
采用被检元件端面安装中心小孔光阑的方法建立光路中心点基准。安装于元件内侧或外测,如图5和图6。装于内测时只有中空部分的加工误差被包含在内,装于外侧时整体的加工误差均含在内。
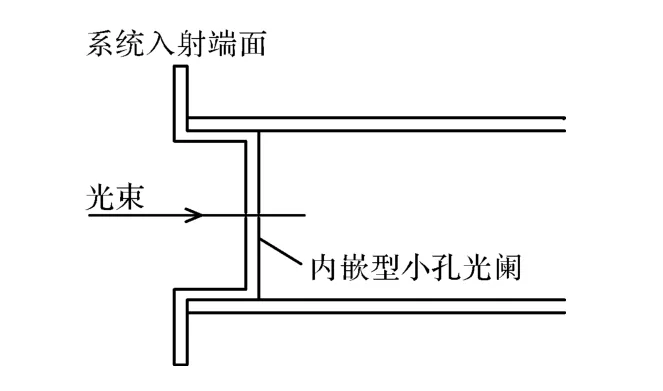
图5 内嵌法小孔光阑安装示意图Fig.5 Schematic of embedded installation of pinhole diaphragm
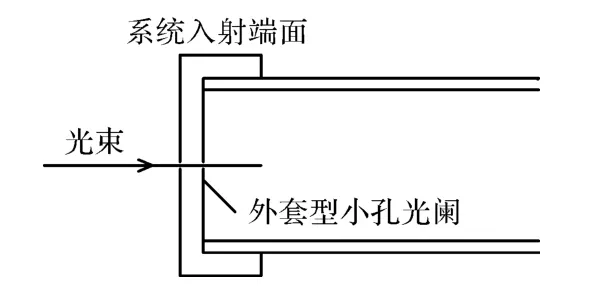
图6 外套法小孔光阑安装法示意图Fig.6 Schematic of wrapped installation of pinhole diaphragm
如图7,设M点为光阑安装于内侧时确定的光路中心,N点为安装于外侧时确定的光路中心,用M和N间的距离Δr来描述2种中心点基准建立方法的差异。易测出值Δr,将待测系统安置在四维调整台上,先用内嵌法安装光阑,让激光束从光阑小孔垂直入射,保持光束不动,将光阑取下后用外套法重新安装光阑,此时光束不能从小孔中心射出,调节四维调整台的水平和竖直位移量,使激光束重新从小孔射出,并记下水平位移调整量Δa和竖直位移调整量
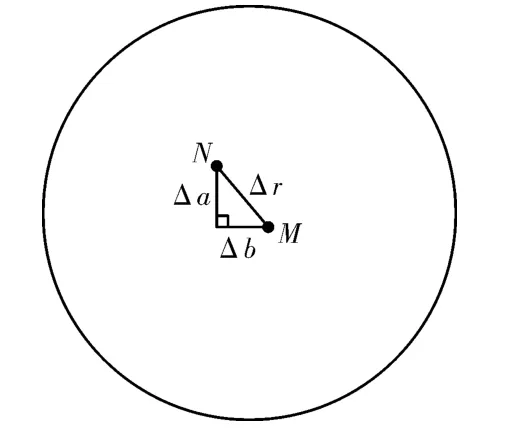
图7 2种中心点基准建立方法之差异Fig.7 Difference between two methods of centre point datum set up
如图8所示,图中省略了机械结构部分,直接画出各光学元件,实际检测中是在机械镜筒两端安装光阑,待测系统可以安装光阑的位置有B的入射端面,B的出射端面,C的入射端面,C的出射端面,E的出射端面。有些端面由于端面结构,只能用内嵌法安装,有些端面只能用外套法安装,还有的两法均可,具体情况见表1,“内(外)”表示该端面既可用内嵌法亦可用外套法安装光阑,检测中选用了内嵌法安装,“内”表示该端面只能用内嵌法安装光阑,“外”表示该端面只能用外套法安装光阑。经测定B入射端面和C出射端面的Δr值约为0.1mm。
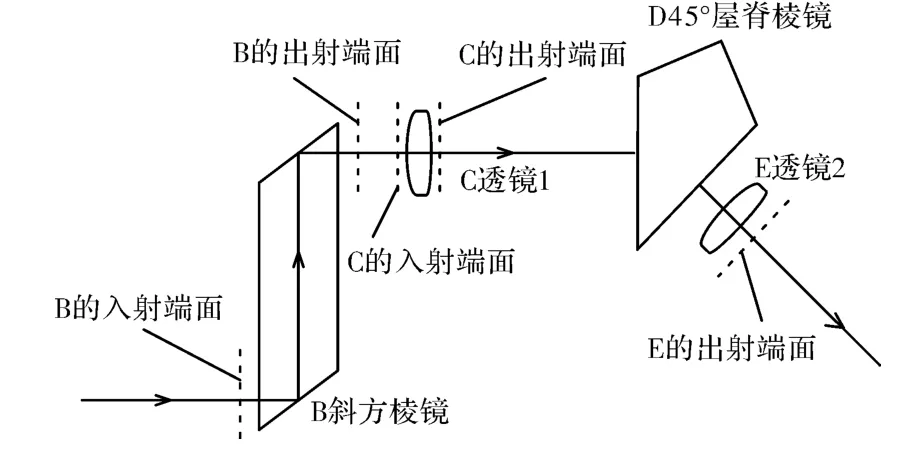
图8 系统端面示意图Fig.8 Schematic diagram of faces of system
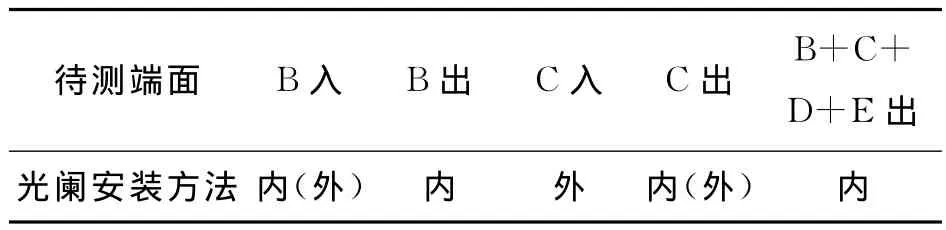
表1 系统各入射端面之光阑安装Table 1 Diaphragm installation of incident faces of system
3.2 系统光路偏转检测
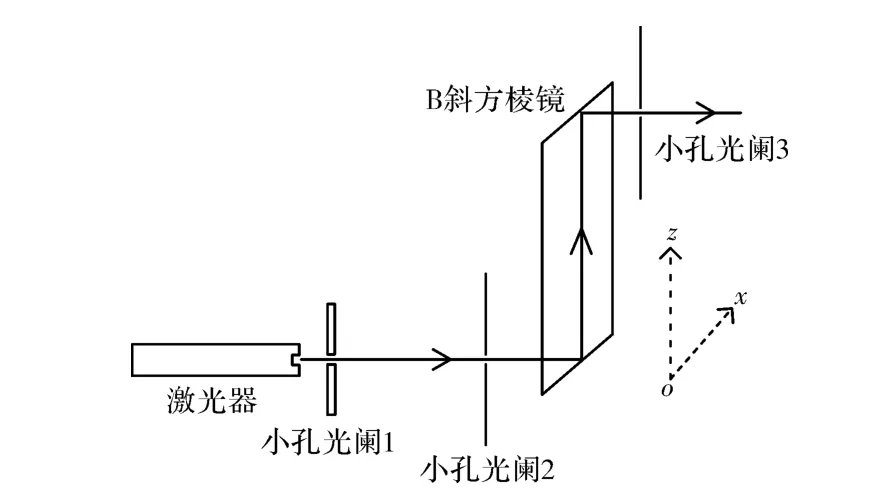
图9 B偏转距离检测示意图Fig.9 Schematic of deflection distance detection of B

图10 B偏转距离检测照片Fig.10 Picture of deflection distance detection of B
光路偏转距离检测。以左光路元件B为例,如图9和图10所示将B放置在四维调整平台上,调节激光使光束入射光斑相对于光阑2中心孔对称分布,同时使斜方棱镜的入射端面反射光点通过小孔光阑1,此时说明激光已校准好,恰好从光阑2中心垂直于斜方棱镜入射端面入射,若激光从小孔光阑3中心孔对称射出,说明偏转距离d为0,若观察到激光从光阑3中心孔非中心对称射出,此时记录调整平台的水平和竖直坐标值x1和z1,然后取下小孔光阑2,微调待测部件的水平和竖直位移量,直到激光恰好从光阑3中心孔对称射出,记录此时的水平、竖直坐标值x2、z2。Δx=x2-x1,Δz=z2-z1即水平偏转距离和竖直偏转距离,为偏转距离d的绝对值。用同样的方法测量了C、B+C、B+C+D+E的光路偏转距离(如图11~图14所示)。检测结果如表2所示,其中“左”表示左光路,“右”表示右光路。
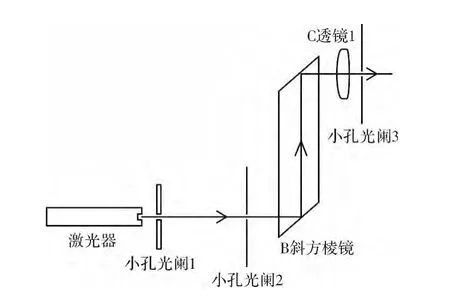
图11 B+C偏转距离检测示意图Fig.11 Schematic of deflection distance detection of B+C
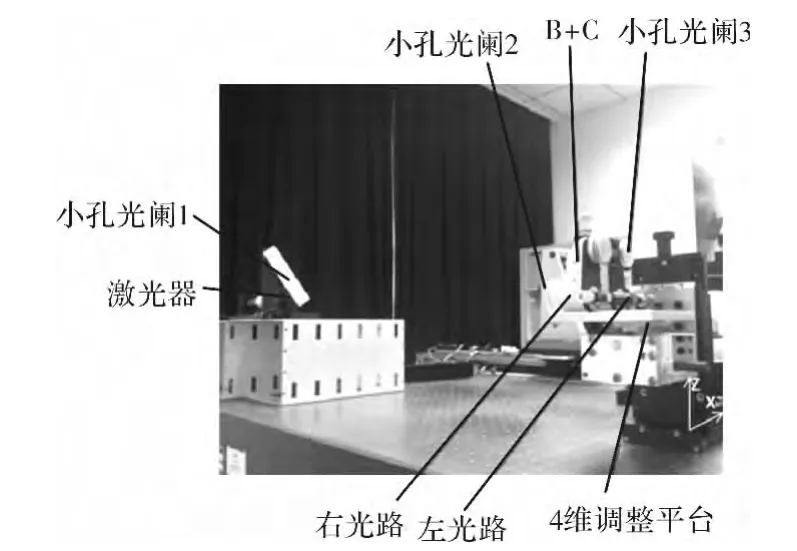
图12 B+C偏转距离检测照片Fig.12 Picture of deflection distance detection of B+C
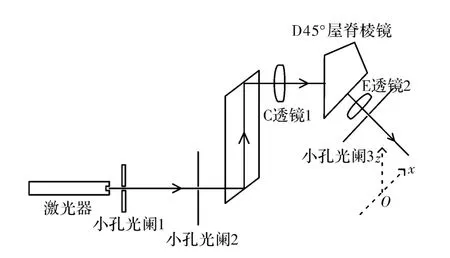
图13 B+C+D+E偏转距离检测示意图Fig.13 Schematic of deflection distance detection of B+C+D+E

图14 B+C+D+E偏转距离检测照片Fig.14 Picture of deflection distance detection of B+C+D+E
光路偏转角度检测。先以左光路为例,如图15调节光路使激光束从B的入射端面中心垂直入射,O点为理想出射光线与斜方棱镜出射端面的交点,A1点是激光束不经过系统直接到达接收屏上的位置,A2点是光束通过B或B+C后到达接受屏的理想位置,A3是光束仅通过B后的实际位置,A4是光束通过B+C后的实际位置,光线通过B后的光路偏转角度为θ1,通过B+C后的光路偏转角度为θ2,近似计算可以认为θ1等于OA2与OA3的夹角,θ2等于OA2与OA4的夹角,e是斜方棱镜的光线横向偏转位移理想值,由待测系统所用斜方棱镜公差图可知e=(51±0.1)mm,取e=51mm,s是斜方棱镜出射端面到接收屏的距离,实验时测得s=5 760mm,选A1为坐标原点,O点坐标为[0,51,-5 760],然后保持入射激光束和接收屏位置不变,换用右光路元件B、C作实验,亦可得到光束通过右光路元件后接收屏上各点的位置,最终如图16所示,“B左”表示把左光路的元件B放入光路中,其他的类同。由以上数据求得光路偏转角度如表3所示。
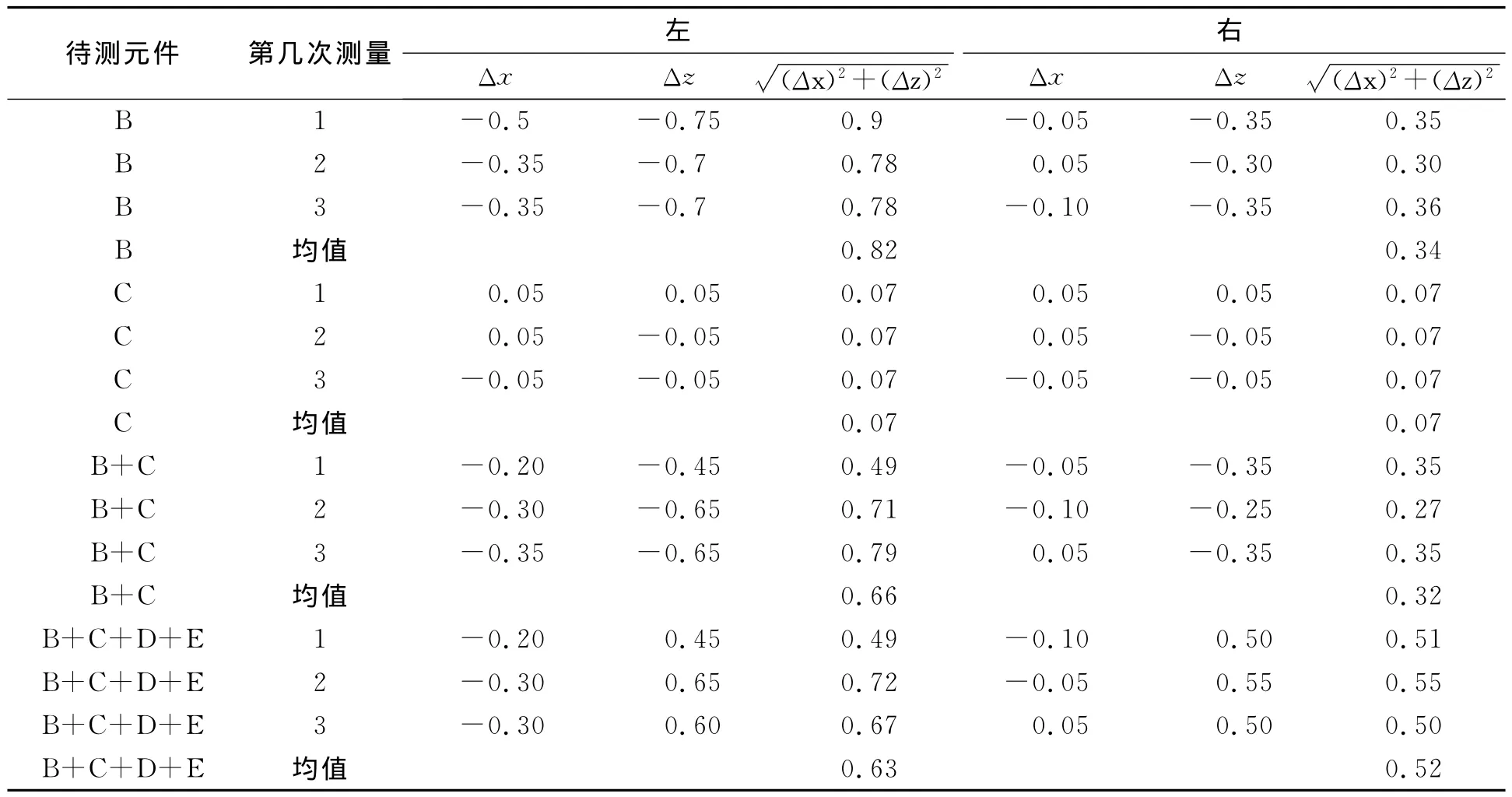
表2 光路偏转距离测量结果Table 2 Measured results of light path deflection distance mm
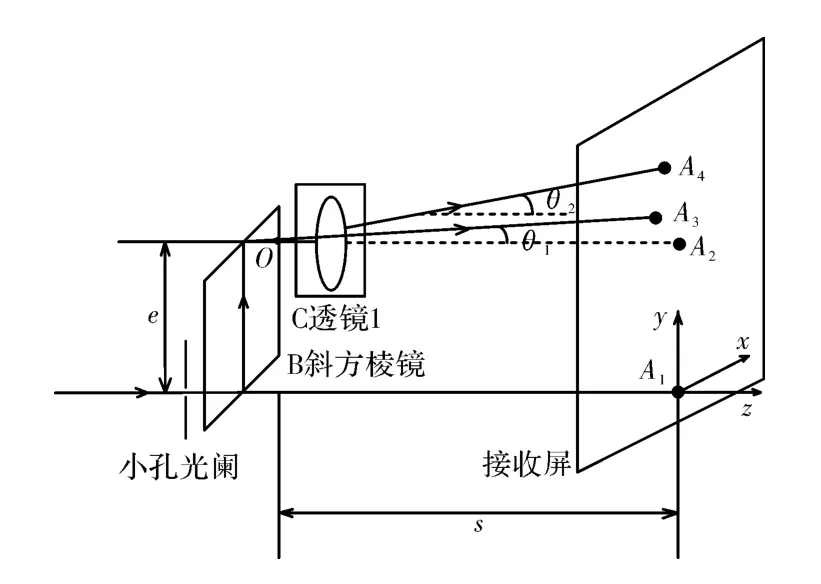
图15 光路偏转角度检测示意图Fig.15 Schematic of deflection angle detection of light path
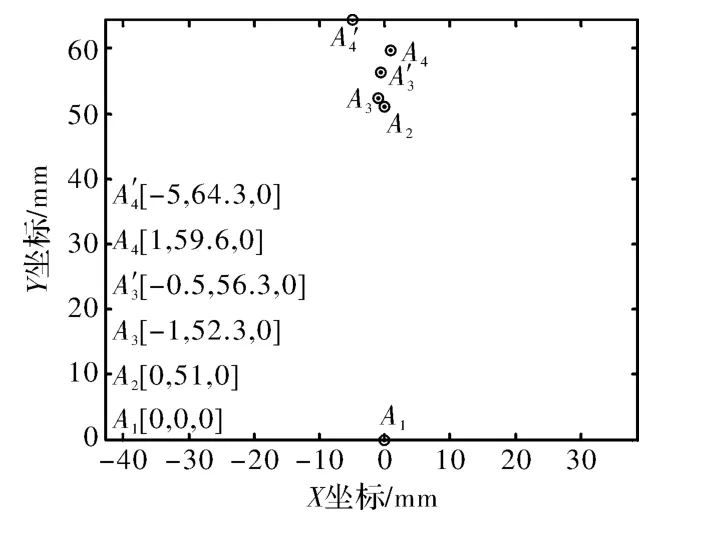
图16 接收屏光点分布坐标图Fig.16 Map of receiving screen light spot location
3.3 系统平行性检测
平行光校准,2束激光分别通过小孔光阑1、2后入射到标准平面镜上,调节激光使2束激光各自的反射光斑分别与光阑1、2的小孔重合,如图17所示。
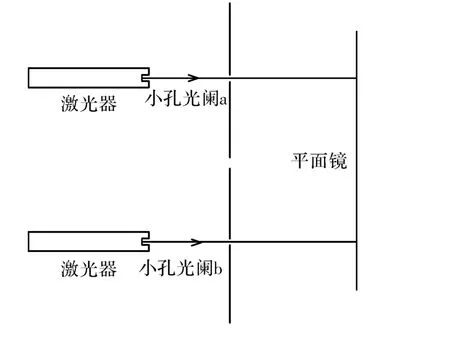
图17 平行光校准Fig.17 Alignment of parallel light
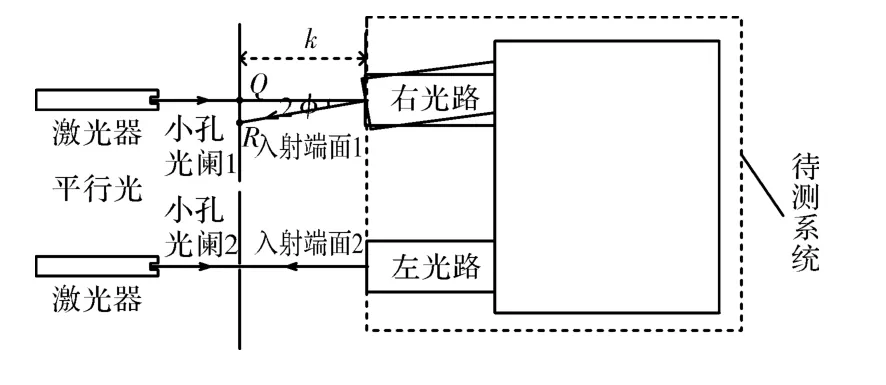
图18 入射端面平行性检测方法Fig.18 Schematic of detection of parallelism between incident faces
两入射端面平行性检测。图18为2束平行光通过小孔光阑后打到入射端面上,调节光路,使光线垂直于入射端面2入射,此时记录入射端面1在小孔光阑1上反射光斑的位置点R,量出其相对于小孔光阑1中心点Q的距离|QR|,小孔光阑1到入射端面1的距离k,则两入射端面夹角φ≈|QR|/2k。
由于A(待测目镜)的入射端面接近平面,亦可用上述方法检测,用上述方法依次检测了A、B、D的入射端面平行性,检测结果如表4所示。
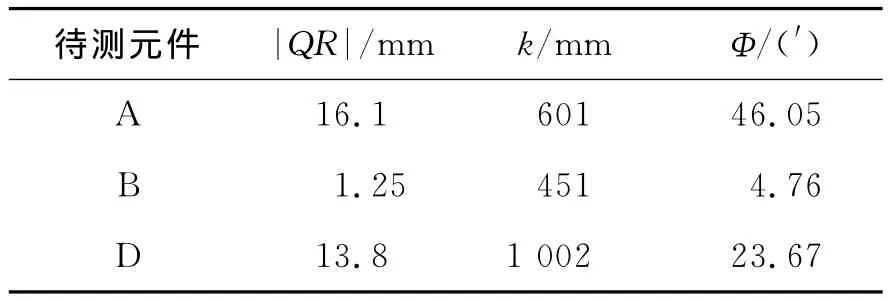
表4 入射端面平行性测量结果Table 4 Measured results of parallelism between incident faces
两光路平行性检测。图19为2束平行光分别从左右光路入射端面中心入射,由于左右光路入射端面不平行,入射时无法使2束光均与端面垂直入射,检测时使左光束垂直于入射端面入射,出射端两光轴间的距离为d1,出射端面到接收屏的距离为s1,两出射光束到达接收屏上的点为B1、B2,间距为d2,依次检测B、B+C、B+C+D+E的两光路平行性,检测中发现O1O2B1B2四点基本上在一个平面内,且O1O2与B1B2大致平行,s1≫d2,s1≫d1,因此有α≈(d2-d1)/s1,测量结果如表5所示。
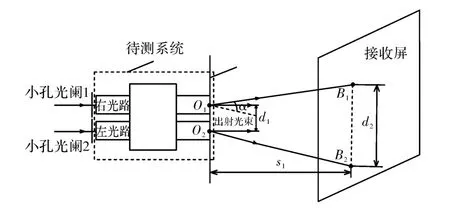
图19 两光路出射光线平行性测量示意图Fig.19 Schematic of emergent light parallelism detection of double-light paths
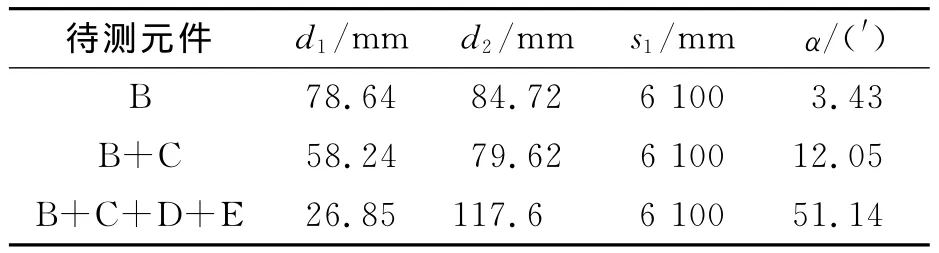
表5 两光路出射光线夹角测量结果Table 5 Measured results of angle between emergent light of double-light paths
4 检测结果分析
光束通过B后出现了较大的偏转距离,左光路为0.82mm,右光路为0.34mm,通过C后,左光路为0.66mm,右光路为0.32mm,偏转距离有所减小,通过D+E后,左光路为0.63mm,稍有减小;右光路为0.52mm,有了明显增大。总体来看,B对控制整个系统的偏转距离大小来说是极为重要的,B造成的偏转距离将影响到后续光学元件,C的影响较小,D+E对偏转距离有放大作用。B大的偏转距离是其加工误差或安装误差过大引起的[4-8]。光束在通过B后的光路偏转角度在几分的数量级,右光路为3.18′,左光路为0.98′,说明左光路B的性能比右光路好,再通过C后,光路偏转角度有所增大,左光路为5.17′,右光路为8.48′,C对偏转角度有放大作用,这使得对B的性能要求增加,更需选用小偏转角的B元件。
A入射端面夹角最大为46.05′,D其次为23.67′,B最小为4.76′,总体上看 A、B、D的入射端面夹角都较大,说明左右光路元件安装对称性较差。平行光通过B后出射光线夹角为3.43′,通过C后增大为12.05′,通过 D和E后增大为51.14′,总体上看,系统的左右光路对称性不太好,放大作用主要是C和E所致,也与D有关。
5 结束语
设计了将系统拆分成元件,再逐步组合分层检测的方法,可以方便地检测分析系统各部件对光路偏转和平行性的影响,以便于逆向设计优化系统。不足之处:1)通过在入射端面安装小孔光阑的方法建立光路中心点基准后,采用的是目视法判断光束是否从小孔中心入射,并通过调节四维支架的位移值来测量偏转距离,速度较慢,精度有限,而且人眼在观察光斑过程中极容易疲劳,如果能研发一种光斑位置探测传感器来替代小孔光阑,直接把光斑位置读出并传输给计算机分析,检测效率和精度都将大大提高;2)检测系统平行性时,由于实验条件所限,没有采用自准直仪[9],若采用自准直仪测量精度至少还可以上升2个量级。
[1] 段学霆.共轴光学系统计算机辅助光轴一致性装调研究[D].西安:中国科学院西安光学精密机械研究所,2006.DUAN Xue-ting.Research of computer aided alignment of coaxial optical system[D].Xi'an:Xi'an Institute of Optics and Precision Mechanics of Cas,2006.(in Chinese with an English abstract)
[2] 王一凡.应用干涉仪对经纬仪光学系统主镜的装调和检 测 [J]. 红 外 与 激 光 工 程,2013,42(5):1275-1279.WANG Yi-fan.Alignment and detecting of photoelectric theodolite system through Utilizing interferometer[J].Infrared and Laser Engineering,2013,42(5):1275-1279.(in Chinese with an English abstract)
[3] 阚珊珊,黄煜,王淑荣.高精度检测球面面形的方法研究[J].光学学报,2005 25(2):195-197.KAN Shan-shan,HUANG Yu,WANG Shu-rong.Methodological disquisition of spherical fine metrical precision[J].Acta Optica Sinica,2005,25(2):195-197.(in Chinese with an English abstract)
[4] 王涌天.复杂棱镜的实际光路追迹[J].光学学报,1991,11(7):640-645.WANG Yong-tian.Ray-tracing formulate for complex prisms[J].Acta Optica Sinica,1991,11(7):640-645.(in Chinese with an English abstract)
[5] 刘树民.高精度棱镜的高效制造技术[J].光学技术,1999(4):70-72.LIU Shu-min.High speed making technology of high-grade prisms[J].Optical Technique,1999 (4):70-72.(in Chinese with an English abstract)
[6] 李政阳,付跃刚.直角屋脊棱镜与立方角锥棱镜的光学特性[J].应用光学,2008,29(5):833-836.LI Zheng-yang,FU Yue-gang.Optical characteristics of right-angle roof prism and corner-cube prism[J].Journal of Applied Optics,2008,29(5):833-836.(in Chinese with an English abstract)
[7] 何平安,王基尧,翁兴涛,等.角锥棱镜直角误差斜入射法检测的理论分析[J].武汉测绘科技大学学报,2000,25(5):449-452.HE Ping-an,WANG Ji-yao,WENG Xing-tao,et al.Theoretical analysis on testing method of corner cube prism's rectangular angle error with inclined incidence[J].Journal of Wuhan Technical University of Surveying and Mapping,2000,25(5):449-452.(in Chinese with an English abstract)
[8] 宫杰,伍凡.施密特屋脊棱镜的角度误差分析及加工工艺方法[J].光电工程,1992,19(3):47-51.GONG Jie,WU Fan.An analysis for angular error and production technology of schmidt ridge prism[J].Opto-Electronic Engineering,1992,19(3):47-51.(in Chinese with an English abstract)
[9] 胡新和,杨博雄.角锥棱镜数字化检测中自准直回像的重影研究[J].光学与光电技术,2010,8(1):91-93.HU Xin-he,YANG Bo-xiong.Research on the layer shadow of collimation echo image in cone prism digitalized testing[J].Optics & Optical Technique,2010,8(1):91-93.(in Chinese with an English abstract
)
