Costas编码信号高分辨动态二维成像方法研究
2014-05-29尚朝轩韩壮志王永磊
王 良 尚朝轩 何 强 韩壮志 王永磊
Costas编码信号高分辨动态二维成像方法研究
王 良*尚朝轩 何 强 韩壮志 王永磊
(军械工程学院电子与光学工程系 石家庄 050003)
Costas编码信号是一种对速度敏感的信号形式,在多目标的情况下,速度补偿不精确时,其较高的旁瓣会淹没较小的目标。论文针对Costas编码信号的这种特点,结合稀疏成份分析的方法,研究了一种高分辨的2维成像方法。该方法根据目标回波在距离-速度是2维稀疏的这一先验信息构造词典,引入波形熵作为信号稀疏性的度量函数,通过对推广的正则化FOCUSS算法进行改进,并采用卡尔曼滤波器进行状态预测,迭代寻找最优原子,实现了动态的距离和速度的高分辨。最后,通过仿真验证了这种方法的有效性,并对算法的容噪性和时效性进行了分析。
高分辨成像;Costas编码;稀疏成份分析;速度补偿
1 引言
Costas编码信号具有理想的图钉形模糊函数,能够同时实现距离和速度上的高分辨,不存在距离-速度耦合现象,同时Costas编码信号又是一种对速度非常敏感的信号,速度的变化会引起距离像的迅速衰减和相位噪声迅速的提高,最终距离像淹没在相位噪声里,因此速度补偿成为这种信号成像的关键。文献[1]针对宽带信号下的高速目标,提出了一种改进的Costas编码跳频信号Stretch处理方法。在多目标多速度环境下,Stretch方法不可能同时实现所有目标速度的匹配补偿,速度补偿不匹配会使整个信号处理的基底噪声增加,RCS小的目标甚至会淹没在相位噪声中,造成严重的遮挡效应,尤其是编码个数比较少的时候,遮挡效应更加严重[2]。文献[3]探讨了多目标散射和多路径传播环境中雷达信号的设计问题,采用在接收机中将两个不同Costas序列跳频编码信号的模糊函数相乘的方法进行旁瓣抑制。近年,更多学者致力于基于Costas编码的复合调制波形的研究:文献[4]将Costas跳频信号和相位编码信号相结合,设计了一种隐蔽性能更好的信号;文献[5,6]从模糊函数和自相关函数的角度分析Costas编码跳频信号和其它调制方式相结合的复合波形的性能;文献[7]结合线性调频信号和Costas频率编码信号设计波形,用于海中目标尺寸的识别。
稀疏成份分析主要是从一个过完备的词典中选择少数几个元素来表示已知的信号,近几年来受到了广泛的关注,为了解决双基地角造成的1维距离像分辨率下降问题,文献[8]针对一类可分稀疏性度量函数,结合最优化理论,研究了稀疏信号重构的快速算法;文献[9]在研究双基地ISAR目标基带回波稀疏性的基础上,提出了利用目标基带回波信号稀疏分解系数生成1维距离像的方法;文献[10]结合贝叶斯模型,在考虑原子之间统计关系的基础上,利用稀疏分解进行信号重构。文献[11]在正则化FOCUSS算法的基础上,提出了推广正则化FOCUSS算法,该算法的稀疏性度量函数更具普遍性,使用方便,稀疏度量值易于求取,具有广阔的应用前景。运动目标的回波由有限个散射点回波叠加组成,每个散射点对应固定的距离和速度信息,信号本质上是稀疏的,Costas编码信号距离像对速度的敏感特性更有利于信号的稀疏表示,因此目标距离-速度的2维像可以通过采用稀疏成份分析的方法得到。本文根据Costas编码信号动目标回波的模型,研究了这种信号进行稀疏成份分析的原子构造方法和算法实现过程,通过选择稀疏度量函数和设置合理的正则化参数,实现了目标距离-速度2维像的高分辨。
2 Costas跳频雷达信号模型分析
2.1 速度对距离像的影响
编码个数为的Costas频率编码脉冲串相参信号的复包络可以表示为

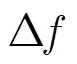

对回波进行码间采样,采样时间为()=iT+/2+2/,对采样信号重新整序并归一化得








2.2 Stretch信号处理方法
传统的Stretch信号处理方法[12]如图1所示,接收机对每个回波脉冲进行码间采样,得到个复数字信号S,这个数字信号经过重新整序,然后经IFFT得到零多普勒频移时的匹配响应输出,同时,信号S和不同的多普勒补偿相位矩阵相乘,然后进行加权处理,再做IFFT得到了对应的多普勒频移时目标的距离像。由于受到发射信号时宽和带宽的限制,传统的Stretch信号处理方法受到距离和速度分辨率的影响,这种信号处理的方法不能分辨在距离或速度上相差小于分辨率的目标。
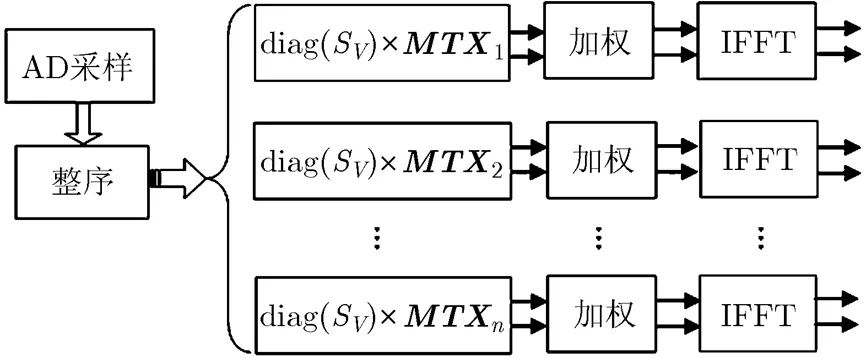
图1 Stretch信号处理框图
3 稀疏成份分析高分辨算法设计
本文针对Costas编码信号对动目标回波模型构造词典,利用稀疏成份分析设计算法,获得目标的高分辨2维像。
3.1 稀疏词典构造方法
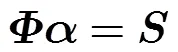

3.2 稀疏度量函数的构造


对于一个波形,若其能量沿参数轴分布越均匀,则波形熵越大;反之越小。由第2节分析知道,目标速度越大,多普勒失配越严重,表现为距离像峰值衰减,能量沿距离轴发散,因此,1维距离像的波形熵在速度轴上具有全局最小值,且位于散射点的径向速度为零的位置。若用波形熵来度量峰值衰减和发散的程度,当目标速度补偿误差为零时,波形熵达到最小。
距离像能量沿距离轴发散越严重,对应像的稀疏性越差,波形熵的最小值与距离像的最稀疏值相对应。以波形熵作为稀疏成份分析的度量函数,波形熵的大小也反映了距离像稀疏性的好坏,如果构造的词典中距离-速度信息和散射点的真实值相同,就能够得到度量函数最小值。令


()在可行集上是凹函数,()也是凹函数,它的局部最小值也就是可行集上的全局最小值。因此,可以用作度量函数进行优化求解。
3.3 算法设计和分析
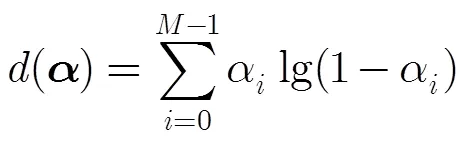
式(12)改写为

推广的正则化FOCUSS算法[11]对回波信号进行稀疏成份分析,对于给定的约束问题,惩罚函数法不一定能够通过有限次的无约束极小化,除非的无约束极小点本身在可行集中[14]。根据乘子法将等式约束的极小化问题转化为

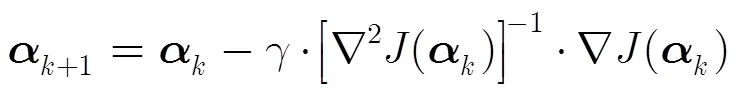

迭代过程中,拉格朗日乘子的选取规则为

为了优化词典,在构造词典的过程中首先采用脉冲累计的方法进行速度估计[15],然后在估计得到的速度周围构造词典,这样可以大大减少词典的维数,减少迭代的次数和计算量。
3.4 动态稀疏成份分析算法

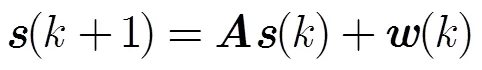
测量方程为
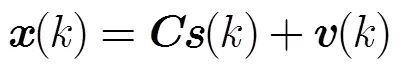
根据包括时间在内的前面全部数据得到的预测方程如下:

其中,预测增益为

预测均方误差为

式(25)和式(26)中,()和()分别为观测噪声()和系统噪声()的协方差矩阵。稀疏成份分析通过迭代计算求解最优原子,迭代的初始值是随机选择的,每次都要经过多次的迭代才能收敛到最优解。
本文提出一种基于卡尔曼预测的动态稀疏成份分析过程,该过程通过信号的过去和当前状态,估计将来的状态,将这个状态赋予稀疏成份分析迭代的初始值,并根据估计状态进行稀疏词典的构造。虽然通过卡尔曼预测得到的初始值仍然存在误差,但相对随机产生的数据已经很接近目标的真值,这样就在一定程度上减少了计算量,提高了稀疏成份分析的效率。动态稀疏成份分析算法的流程图如图2所示。

图2 算法流程图
4 仿真分析
4.1 算例仿真

目标的4个散射点在初始时刻的距离参数为r= [372.60, 373.77, 370.61, 373.43] m,各散射点对应的速度为v=[-5.83, -5.66,-5.81, -6.02] m/s,对应的散射系数为=[1.00, 0.43, 0.12, 0.13]。根据第3节分析,用乘子法将等式约束寻优问题转化为无约束寻优问题,设置正则化参数=1,拉格朗日乘子=0进行仿真,重新构造词典,进行稀疏成份分析,得到距离-速度2维像如图5所示。图中各个峰值的位置反映了目标距离、速度和散射强度的大小,验证了算法的正确性。同时,由于散射点的距离和速度参数没有在整数倍的分辨率上,造成2维像能量向附近距离-速度单元的泄露,从而使对应的散射点的散射强度有所衰减。
采用动态的稀疏成份分析算法,首先根据散射点之前的状态对将来的状态进行预测,然后根据状态预测值构造词典,设置迭代原子初始值,进行40 s的仿真,得到所有散射点的距离和速度变化情况如图6所示。图6是一个3维图,由一组的2维像组成,在目标运动的整个过程中,所有散射点相对雷达的高分辨距离和速度信息,各个散射点的强度信息都反映在了图上,更加有利于目标识别。
4.2 仿真结果分析
4.2.1高效算法分析 本文3.5节中提出用Kalman滤波的方法进行状态预测,并将状态预测的结果用于词典构造和原子初始化,这在一定程度上减少了寻优过程中的迭代次数,从而减少了计算量。仿真过程中,采用和未采用Kalman滤波进行寻优,迭代次数的统计结果如图6所示。其中,未采用Kalman滤波的迭代次数的均值为70.8次,采用Kalman滤波之后的均值为50.3次,计算量下降了30%。
在原子寻优的过程中,高分辨成像需要构造的词典和原子阶数都很高,因此每步迭代的计算量都很大,随着Costas编码阶数越高,计算量越大,收敛速度越慢。对仿真各个阶段耗时进行监测,得到寻优过程耗时最多的是式(19)中的求逆运算,平均约0.104 s,而其余的运算只用0.065 s。因此只需要提高求逆的运算速度,就能够提高整个寻优的效率。在应用过程中,可以考虑采用以下方法提高矩阵求逆的效率:
(1)采用Q-R分解代替式(19)的求逆过程,这在相控阵雷达的STAP信号处理中经常用到。
(2)根据其它成像算法得到的先验信息,对词典进行降维处理,减少无用的基,降低矩阵的阶数。
4.2.2容噪性分析 杂波和噪声会对高分辨成像带来很大的影响,特别是在信噪比较小(< 10 dB)的情况下,因为这时信号稀疏性的先验信息不再成立。在一定信噪比下,可以通过调整正则化参数来调整信号稀疏表示和误差之间的平衡,进而实现信号的稀疏表示。为了评估算法的容噪性能,采用信号失真度[16]进行分析。信号的失真度采用归一化的均方误差来衡量,定义为
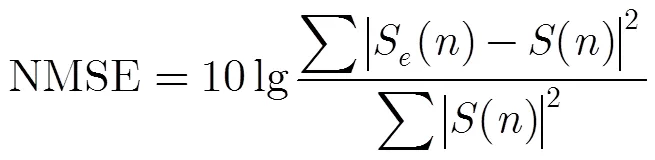
其中()为没有噪声的情况下回波的高分辨像,S()为有噪声的情况下回波的高分辨像,2维像的失真表现为峰值的衰减和2维像位置的误差,这都会给目标的检测和识别带来影响。图8给出了不同信噪比下高分辨像的信号失真度,从图中可以看出,在一定信噪比下,2维像的失真还是很小的,在允许的误差范围内,并且信噪比越高,2维像的失真度越小。
5 结束语
稀疏成份分析和实际的物理现象相结合,在信号分析和超分辨重构方面具有很好的应用价值。本文根据回波信号在距离-速度2维像上的稀疏特性,结合Costas编码信号回波的特点,采用波形熵作为稀疏性的度量函数,构造词典设计稀疏成份分析算法,并用卡尔曼滤波器进行动态状态预测,在采样率有限的情况下实现了2维像的高分辨,避免了大目标旁瓣对小目标的遮挡,并且实现了散射点距离、速度和散射强度等信息的精确探测,在目标识别中具有很高的应用价值,最后对算法的高效算法和容噪性进行了分析。这种算法虽然提高了分辨率,同时也增加了算法的复杂度,更高效的词典构造方法和更快速的实现算法仍需进一步研究。
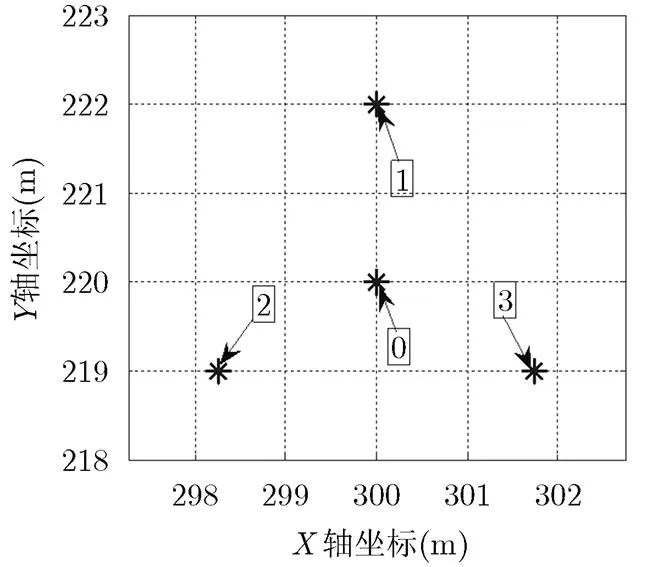
图3 散射体模型

图4 目标运动轨迹

图5 4个散射点通过稀疏成份分析得到的2维像
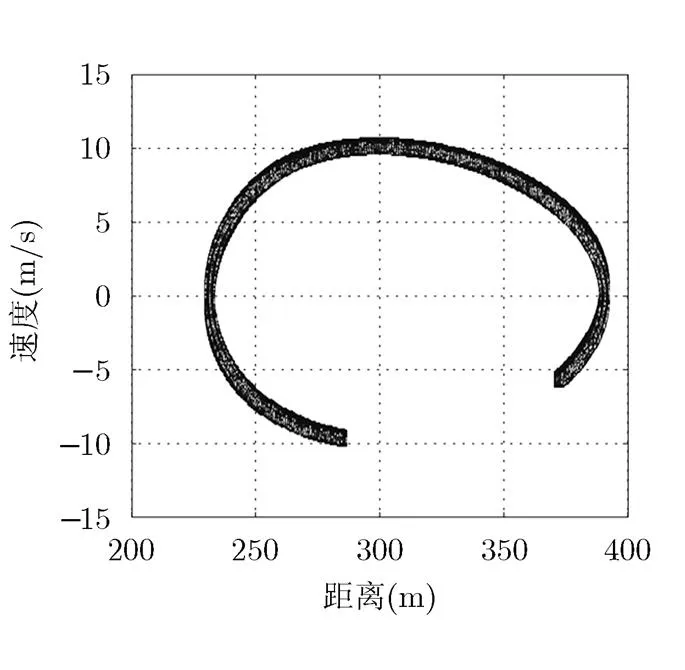
图6 目标散射点信息变化情况
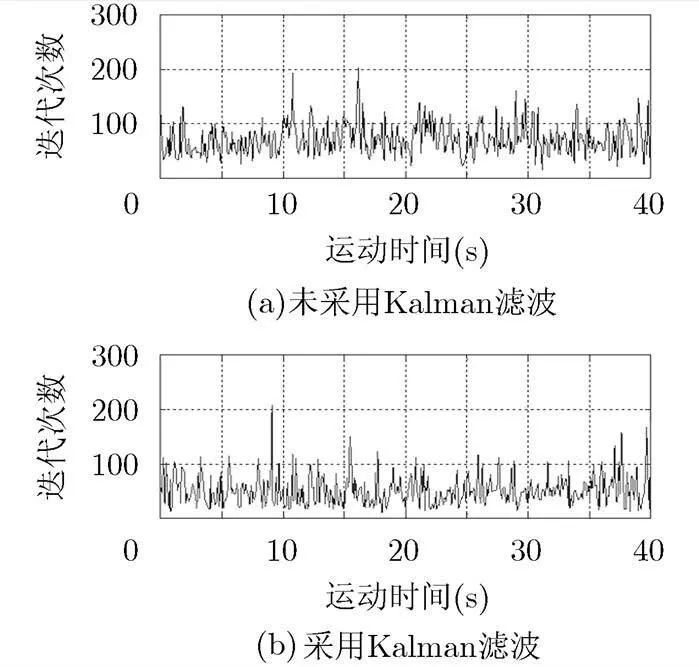
图7 迭代次数对比

图8 不同信噪比的信号失真度
[1] 魏玺章, 刘振, 邓斌, 等. Costas编码跳频宽带雷达信号测速技术研究[J]. 电子学报, 2010, 38(10): 2426-2429.
[2] Levanon N. Stepped-frequency pulse-train radar signal[J].-, 2002, 149(6): 297-309.
[3] 姚建国, 黄清. Costas序列在多目标散射雷达系统中的应用研究[J]. 南京邮电大学学报(自然科学版), 2010, 30(4): 61-70,74.
[4] Yang Hong-bing, Zhou Jian-jiang, Wang Fei,.. Design and analysis of Costas/PSK RF stealth signal waveform[C]. Proceedings of 2011 IEEE CIE International Conference on Radar, Chengdu, China, 2011: 1247-1250.
[5] Guang Hua and Saman Abeysekera. Collocated MIMO radar waveform coding using Costas and Quadratic Congruence arrays[C]. 2011 8th International Conference on Information, Communications & Signal Processing, Singapore, 2011: 1-5.
[6] Pace P E and Ng C Y. Costas CW frequency hopping radar waveform: peak sidelobe improvement using Golay complementary sequences[J]., 2010, 46(2): 169-170.
[7] 李永胜, 吕林夏. LFM-Costas编码信号在水下目标识别中的应用[J]. 舰船科学技术, 2012, 34(6): 74-78.
[8] 韩宁, 尚朝轩. 基于粒子群优化的稀疏分解变尺度快速算法[J]. 系统工程与电子技术, 2012, 34(1): 46-49.
[9] 韩宁, 尚朝轩, 何强, 等. 基于稀疏分解的双基地ISAR一维距离成像方法[J]. 信号处理, 2012. 28(1): 54-59.
[10] Peleg T, Eldar Y C, and Elad M. Exploiting statistical dependencies in sparse representations for signal recovery[J]., 2012, 60(5): 2286-2303.
[11] 杜小勇, 胡卫东, 郁文贤. 推广的正则化FOCUSS算法及收敛性分析[J]. 系统工程与电子技术, 2005, 27(5): 922-925.
[12] Levanon N and Mozesona E. Radar Signals[M]. New Jersey: John Wiley & Sons, 2004: 74-99.
[13] Du Xiao-yong, Hu Wei-dong, and Yu Wen-xian. A criterion for the construction of a regularization function in sparse component analysis[J].,,, 2005, 24(4): 315-325.
[14] 粟塔山. 最优化计算机原理与算法程序设计[M]. 长沙: 国防科技大学出版社, 2001: 151-164.
[15] 王良, 何强, 尚朝轩, 等. Costas编码跳频信号自测速方法研究[J]. 现代雷达, 2013, 35(1): 24-28.
[16] 原浩娟, 刘国满, 姜伟, 等. 步进频信号距离-多普勒成像的干扰抑制[J]. 系统工程与电子技术, 2009, 31(9): 2059-2062.
王 良: 男,1983年生,博士生,研究方向为雷达信号处理和目标探测.
尚朝轩: 男,1964年生,教授,研究方向为武器系统性能检测与故障诊断.
何 强: 男,1972年生,副教授,研究方向为雷达信号处理、语音信号处理.
Study on Two-dimensional High ResolutionDynamic Imaging Algorithm of Costas-coded Signal
Wang Liang Shang Chao-xuan He Qiang Han Zhuang-zhi Wang Yong-lei
(,050003,)
Costas-coded Frequency Hopping (FH) signal is very sensitive to velocity changes. As a result, in multi- targets scenario, sidelobe pedestal arisen induced by inaccuracy compensation will make possible masking if one target is much stronger than the others. Based on this property of Costas-coded FH signal a high resolution rang- velocity two-dimensional imaging algorithm is studied by using sparse component analysis. Echoes can be regarded to be sparse in rang-velocity dimensions, and a sparse dictionary is constructed based on the sparsity feature, where the waveform entropy is used as the sparse measuring function. By improving the generalized regularized FOCUSS algorithm and making use of Kalman filter, the best atom can be found iteratively and high resolution in rang and velocity is realized. The algorithm is validated by simulations, and the noise tolerance as well as the time effectiveness are analyzed.
High resolution imaging; Costas-coded; Sparse component analysis; Velocity compensation
TN957.52
A
1009-5896(2014)03-0559-06
10.3724/SP.J.1146.2013.00829
2013-06-07收到,2013-09-09改回
国家自然科学青年基金(51107147)资助课题
王良 kevin20911@163.com
