创设对称性简化积分计算的几种方法

左俊梅

（周口师范学院数学与统计学院 河南周口 466001）

创设对称性简化积分计算的几种方法

左俊梅

（周口师范学院数学与统计学院 河南周口 466001）

本文对积分区域不具有对称性的情形，总结了几种方法来创造对称性，如平移变换、伸缩变换、区域划分等，从而简化积分运算。

对称性；平移变换；积分计算；伸缩变换

在积分计算中，运用积分区域的对称性和被积函数的奇偶性可以简化计算，当积分区域不具有对称性时，我们也可以通过适当的变换来创造对称性。本文总结了几种创造对称性的方法。

方法一：通过区域划分来创造对称性

当积分区域不具有对称性时，如果可以将区域划分为几个部分，其中每个部分都具有对称性，就可以根据积分的性质以及前面得出的对称性定理来简化每一部分积分的计算，从而达到简化整个积分计算的目的.

方法二：通过平移变换来创造对称性

当积分区域关于某条平行于坐标轴(或坐标平面)的直线(或平面)对称或关于某一点(非原点)对称时，可以通过平移变换将区域化为关于坐标轴(或坐标平面)对称或关于原点对称的情形，进而可以简化计算.

方法三：通过伸缩变换来创造对称性

当积分区域不具有对称性(主要指轮换对称性)时，可以通过伸缩变换来创造对称性，比如当积分区域为椭圆、椭球体等时，若根据其它对称性不能简化计算，可以通过伸缩变换将区域化为圆、球等，再利用轮换对称性简化计算.有时我们需要先进行平移变换，再进行伸缩变换，如中心不在原点的椭圆.

方法四：对具体问题作具体变换

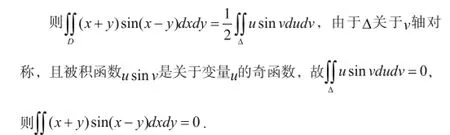
[1]严水传.关于对称性在积分计算中的应用补遗[J].高等数学研究,2002(5):28-31.

[2]李久平.广义对称性在积分计算中的应用[J].工科数学,2001,17(3):97-99.

On several methods create symmetry to simplify integral calculation

Zuo Jun-mei
(College of Mathematics and Statistics Zhoukou Normal University, Zhoukou Henan, 466001, China)

This paper has no symmetry of integral area situation, summarizes several methods to create symmetry, such as translation, scaling, division, thus simplifying the integral operation.

symmetry; translation; calculation; stretching transformation

O172.2

A

1000-9795（2014）04-0037-01

［责任编辑：董 维］

2014-02-15

左俊梅（1986-），女，河南周口人，助教，从事分形几何与小波分析方向的研究。