基于混沌与分形理论的电机故障诊断方法

温 华

（山西焦煤集团公司机电部，山西太原030024）

基于混沌与分形理论的电机故障诊断方法

温 华

（山西焦煤集团公司机电部，山西太原030024）

通过对鼠笼式异步电机故障电流信号的研究，提出了一种基于混沌以及分形理论的电机故障诊断方法。用互信息量确定了信号时间序列相空间重构的最佳延时，并对关联维数、分形维数进行了分析和计算，探讨了故障和正常状态下信号的混沌及分形特性。根据电机定子电流在不同工作情况下的分形维数和关联维数，便可确定电机故障的类型。

混沌理论；分形；故障诊断；相空间重构；盒子维数；关联维数

三相交流异步电动机是应用非常广泛的电气设备，在电力系统中，异步电机用电量占整个系统总用电量60%以上。因此，研究电机故障诊断方法，准确诊断出电机故障，对于保证电机设备安全运行以及保障企业安全生产，具有重大经济和社会意义。

在异步电机中，大中型异步电机多采用鼠笼型转子。由于电机启动时，转子绕组内流过很大电流，导条承受较大冲击力，很快升温，产生热应力，并承受离心应力。电机在反复启动、运行、停转时，导条和端环受到循环热应力和变形作用。由于受力不均匀，导条因应力不均匀而断裂。目前，使用较多的在线监测方法有：功率谱分析、小波变换、Fourier频率谱分析、Park矢量法和扩展Park矢量法以及神经网络遗传算法、灰色理论等。

1 基本理论

1.1 分形理论概述

分形理论属于非线性科学，由IBM的法国数学家B.B.Mandelbrot于1975年创建。分形学试图通过混乱现象和不规则构型，揭示隐藏在它们背后的局部与整体的本质联系和运动规律。分形中的常用维数有：Hausdorff维、分形维和盒维（box dimension）。关联维数属于混沌学的范畴。

1.2 盒维数

盒维数是一种普遍使用的维定义，它易于数学计算和实验测量，出现在20世纪20年代并冠以种种其他名称，如度量维、信息维、Kol-Mogorov熵、熵维以及容量维等。由于它是1929年首先被Bouligand引入，故又称Bouligand维。其定义如下：

F是Rn中的非空有界子集，记N（A，δ）表示最大直径为δ且能够覆盖F集合的最小数，则F的盒维数定义为：

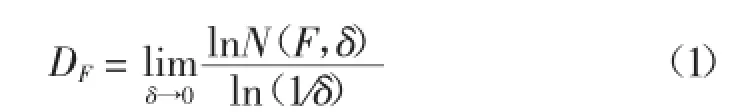
在双对数图上画出lnN（F，δ）对lnδ的曲线，其直线部分的斜率即为该分形体的盒维数。

1.3 关联维数

Grassberger和Procaccia根据嵌入理论和重建相空间思想，提出了用时间序列直接计算关联维数的算法—GP算法。

设（xi，i=1，2，3，…，N）为一时间序列，将其嵌入到m维欧式空间Rm中，得到一个向量集J（m），其元素记为：

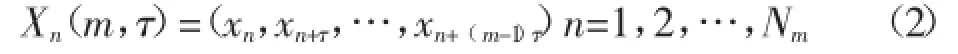
式中:τ=kΔt是固定时间间隔，即时间延迟；Δt为采样间隔；k为整数。

从这Nm个点中任意选定一个参考点Xi，计算其余Nm－1个点到Xi的距离：

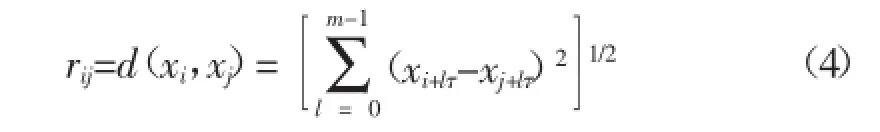
对于任意给定的一个数r＞0，相关函数的定义如下：

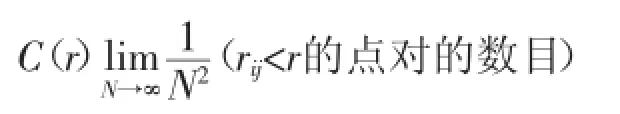
其表示在重构的相空间中距离小于r的点占所有点的比例。

r的取值范围（尺度变换）受到大小两端的限制，r取值过大，相关函数C（r）=1，这样的r值不能反映系统内部的性质。r取值过小，相关函数C（r）=0，这时r又不能反映客观实体。可见，r取值一定要适当，有关系式：

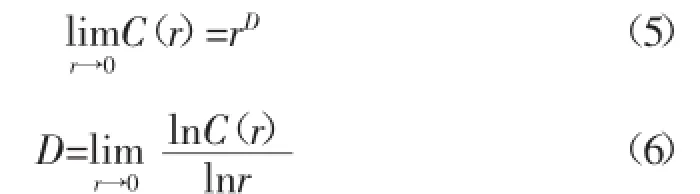
式中，D称为关联维数。

其中：

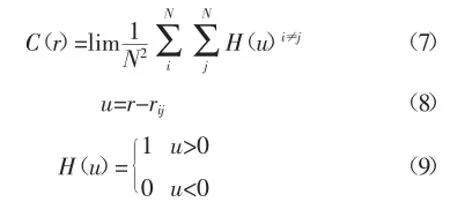
在实际应用中，常给定一些m的值，画出lnC（δ）－lnδ的曲线，除斜率为0或m的直线外，考察其间的最佳拟合直线，则该直线的斜率就是关联维数D。为使m的选择合适，可以增大m，通常D也相应增大，直到m= mmin，此时D不再增大且近乎不变，mmin就可以视为能容纳该分形吸引子的最小重构相空间维数。

2 实例分析

在进行了电机故障实验之后，采集了以下4种情况：正常工作情况、1根导条断裂、3根导条断裂和匝间短路电机的定子电流数据，因为是三相对称电流，所以只对A项数据进行处理。1根导条断裂电机的A相定子电流时域波形图见图1。

2.1 降噪

在所采集的数据中，存在许多高频信号，即噪声，这样的噪声会对计算结果产生影响，故先对数据进行小波降噪处理。降噪前后的波形对比见图2。

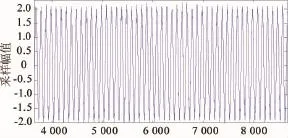
图1 1根断条A相定子电流时域波形图

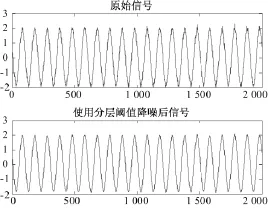
图2 降噪前后波形图对比图

2.2 计算盒维数

将计算盒维数的理论公式编写为程序，对所得电流序列进行盒维数计算，得到如下数据，见表1。

表1 不同工作情况下的盒维数表

通过对比表1数据，可以发现，故障电机的分形维数较低，且断条故障电机维数高于偏心启动故障电机，好电机分形维数最高。其中，断条越多，分形维数越低，这符合实际情况，因为断条数越多，说明电机故障越严重。所以，用盒维数来诊断电机故障时，可以通过盒维数的大小初步判断发生哪种故障以及故障的严重程度。

2.3 找时间延迟常数

根据互信息量方法的递归算法，将实验所采集的离散点进行处理，得到互信息量随延时变化的曲线。无故障电机、1根导条断裂、3根导条断裂和偏心启动故障电机的曲线见图3。

由图3得知，无故障电机在延时为4时就达到了第一个最低点，1根断条在延时为3时达到最低点，3根断条在延时为25左右时达到最低点，偏心启动在延时为28左右第一次达到最低点。因此，可得到不同工作情况下的时间延迟表，见表2。

分析以上数据，可以得出如下结论：无故障电机和1根断条电机互信息量随时间延时变化较快，而3根断条电机和偏心启动电机的互信息量则随时间变化缓慢，且3种故障的时间延迟各不相同。因此，根据时间序列互信息量随延时的变化同样可以较有效地检测电机故障。

2.4 确定嵌入维数

由前面的理论推导可知，混沌特征值是随嵌入维数的不同而改变的，因此，要较为准确地找到特征值趋于不变时的嵌入维数，在此嵌入维数下计算的关联维数才较为准确。利用Cao方法求出的无故障电机、1个断条电机、3根断条电机以及偏心启动电机的特征值随嵌入维数变化的曲线见图4。

分析图4，最终确定各类故障嵌入维数见表3。

2.5 计算关联维数

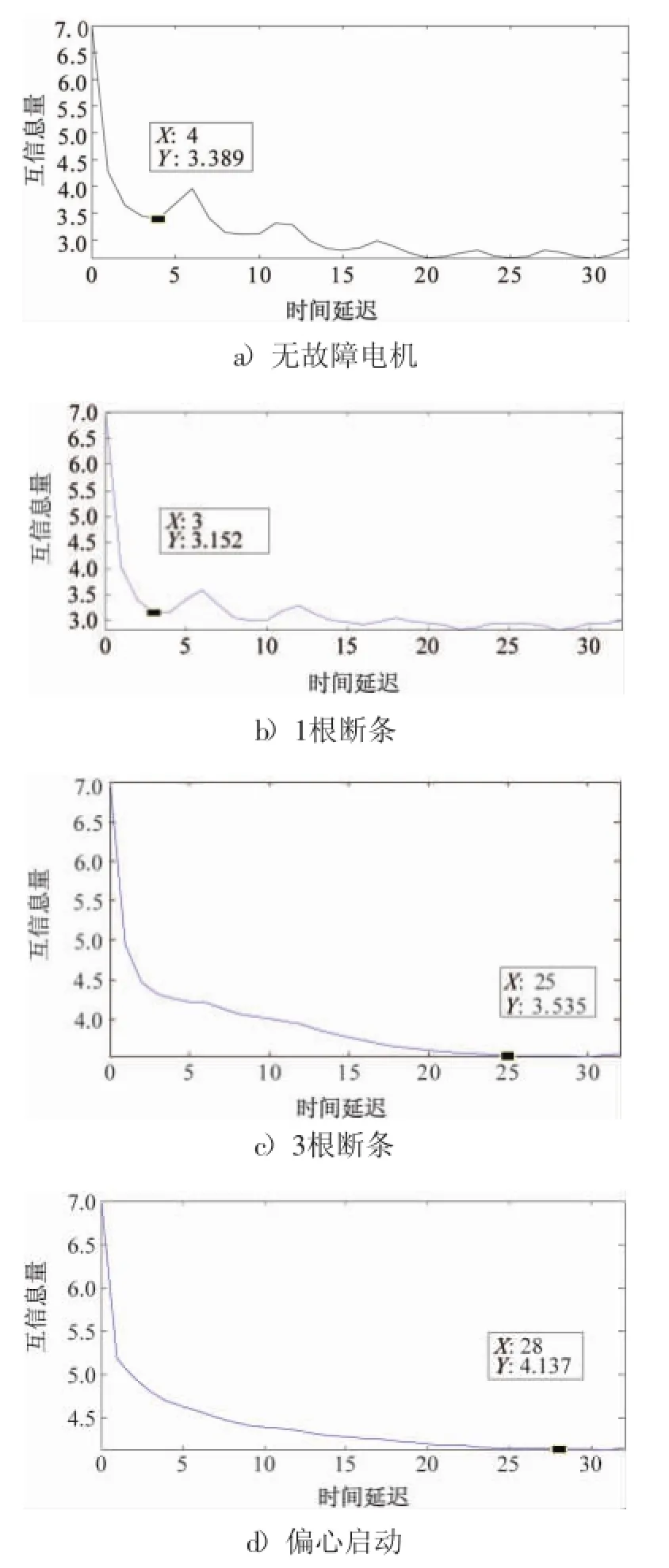
图3 各类故障的互信息量与时间延迟示意图

表2 不同工作情况下的时间延迟表

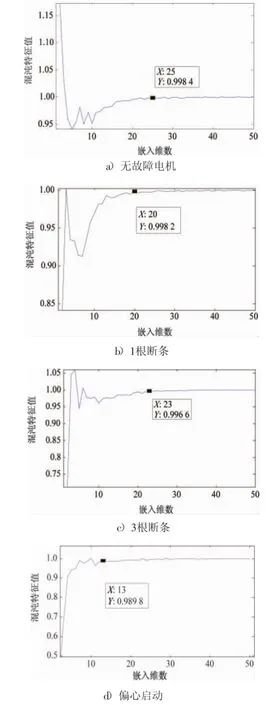
图4 各类故障的混沌特征值与嵌入维数图

得出了时间延迟常数和嵌入维数，接着进行相空间重构，进而求取关联维数。关联维数的函数是两个对数的比值极限，因此，其在图形中的含义便是双对数关系曲线的斜率。可先画出其双对数曲线，然后编程求取斜率，即为对应情况下的关联维数。无故障电机的双对数曲线见图5。

表3 不同工作情况下的嵌入维数表

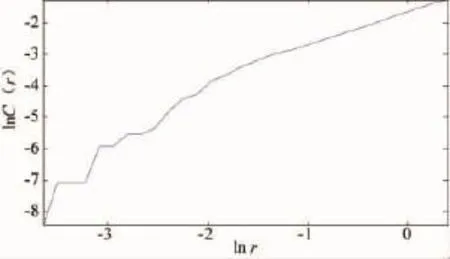
图5 无故障电机双对数曲线图

把其他3种故障情况下的双对数曲线画出后，便可以得到时间序列的关联维数，见表4。

表4 不同工作情况下的关联维数表

分析表4中数据可得出：对于不同的故障情况，其关联维数不同，且无故障电机关联维数最大，随着断条数增加，关联维数逐渐降低。故可用关联维数来检测电机故障。

3 结论

通过对无故障电机和故障电机定子电流（A相）的分形和混沌特征进行分析，得出了故障电机电流序列的盒维数和关联维数均低于正常电机，且不同故障情况下的分形和混沌特征也有较为明显的区别，因此，可以用盒维数和关联维数对电机故障进行在线检测。

［1］李立华，张强.基于混沌理论的金融系统稳定性研究［J］.经济数学，2010，27（4）:62-72.

［2］谢忠玉，张立.相空间重构参数选择方法的研究［J］.中国科技信息，2009，27（16）：84-90.

［4］陈引峰，李继伟.黑河日径流量混沌变化特性研究-Ⅱ相空间嵌入维数的确定［J］.地下水，2010，32（6）:143-144.

［5］陈伟根，云玉新，杜林，等.基于互相关和李雅普诺夫指数的微弱正弦信号混沌检测［J］.电力系统自动化，2008，32（18）:44-48.

［6］马骏，张印硕，曹占辉.基于Cao方法的空间目标RCS混沌性分析［J］.现代雷达，2009，31（5）:61-64.

［7］李春胜，王宏.脑电Alpha波的混沌关联维数分析［J］.仪器仪表学报，2009，30（3）:477-480.

［8］王凤利，赵德有，马孝江.基于局域波和混沌的转子系统早期故障诊断［J］.大连理工大学学报，2009，49（1）:77-81.

［9］王炳成，任朝晖，闻邦椿.故障诊断中的混沌参数分析［J］.机床与液压，2010，38（23）:144-147.

［10］周力行，李毅，窦鹏，等.混沌-分形理论在变压器油热老化故障诊断中的应用［J］.电工技术学报，2008，23（12）:28-34.

［11］史丽晨，段志善.基于混沌-分形理论的往复式活塞隔膜泵磨损故障分析［J］.农业机械学报，2010，41（4）:222-226.

［12］赵经，张杨，朱立宗，等.基于分形理论的滚动轴承故障诊断的研究［J］.洛阳理工学院学报（自然科学版），2008，18（1）:43-44.

［13］杨永发，张杨，许鹏辉.基于分形理论的旋转机械故障诊断的研究［J］.煤矿机械，2008，29（2）:207-208.

［14］谢文彪，樊绍胜，费洪晓，等.基于互信息梯度优化计算的信息判别特征提取［J］.电子与信息学报，2009，31（12）:2975-2979.

Motor Fault Diagnosis Methods Base on Chaos and Fractal Theory

Wen Hua

By studying the signal of squirrel-cage asynchronous motor fault current，an diagnostic method bases on chaotic and fractal theory about motor fault is proposed.The best delay of the phase space reconstruction of signal time series are determined by using mutual information，and calculates and analyzes the correlation dimension and fractal dimension，discusses the chaos and fractal characteristics of signal in fault and normal state. According to fractal dimension and correlation dimension of motor stator current under different working condition，determines the type of motor fault.

Chaos theory；Fractal；Fault diagnosis；Phase space reconstruction；Box dimension；Correlation dimension

TD60

A

1672-0652（2014）12-0025-04

2014-11-08

温华（1977—），男，山西灵石人，2000年毕业于太原理工大学，工程师，主要从事机电管理工作，（E-mail）wen_h@139.com