基于ACO 优化小波神经网络的语音识别

赵 群

(渤海船舶职业学院，辽宁 葫芦岛125003)

语音识别技术经过几十年的发展，目前已经取得了长足的进步。实际环境中总是存在各种各样的噪声，噪声的存在会使得所提取的语音特征参数数据产生偏差，噪声越大所产生的偏差也会越严重，从而使识别系统的性能下降，正确识别率会降低直至识别系统完全失效。

长期以来，语音识别系统大多采用概率统计模型，概率统计模型适合于对海量数据进行训练，从本质上来说，它是是一种浅层网络建模，所以概率统计模型是不能充分描述特征的状态空间分布的。人工神经网络的原理是模拟人脑的多层结构，通过采取逐级进行信息特征抽取的方式，最终得到适合进行模式分类的性能优良的特征，从而大幅度提升语音识别系统的识别率。

蚁群优化(Ant Colony Optimization，ACO)算法是一种优化算法，该算法根据多个蚂蚁算法所归纳得出，用于解决复杂的组合优化问题［1］。本文首先对蚁群算法的原理和算法的结构框架进行研究，在此基础上，把蚁群优化算法与小波神经网络进行有机的组合，建立蚁群优化小波神经网络。研究了蚁群优化算法训练小波神经网络的基本原理和方法步骤。并与BP 算法、遗传算法、模拟退火算法进行性能比较，将各种方法训练的小波神经网络用于噪声背景下的语音识别，最后，进行仿真实验来验证所研究方法的有效性。

1 小波神经网络

小波神经网络(Wavelet Neural Network，WNN)是一种比较新颖的神经网络模型，该模型是基于小波变换所构造而成的，小波神经网络结合小波变换和神经网络的特点(小波变换良好的高频域时间精度、低频域频率精度，神经网络的自学习能力)，因而具有很强的容错能力和逼近性能。

小波变换定义如下:

设ψ(t)∈L2(R)，(L2(R)代表的是实数空间，该空间平方可积，即能量有限)，对ψ(t)进行傅里叶变换，结果用Ψ(ω)表示。当Ψ(ω)满足条件

时，ψ(t)被称作是基本小波或者称作母小波(Mother Wavelet)，将母小波函数ψ(t)进行伸缩变换和平移变换以后，得到的将是一个小波序列:

式中a 为伸缩因子，b 为平移因子。

对于任意的函数f(t)∈L2(R)，其小波变换定义为:其逆变换(重构公式)为:

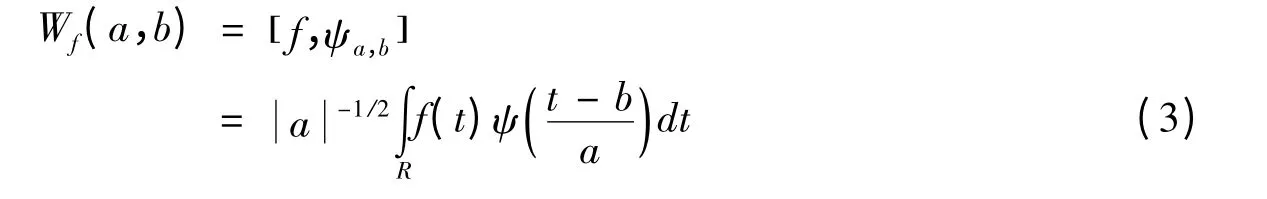
将(4)式离散化，可以得到:

公式(5)中k 表示的是小波基的个数，对公式(5)的理解是:由加权小波基做线性叠加可以构建得到原信号函数。公式(6)给出的是一个三层前向神经网络的输出:

式中i 代表的是第i 个神经元的序号，神经元激励函数用f(x)表示，加权系数为ωi，xi代表输入，θi表示偏移量。

将公式(5)和公式(6)进行对比，可以得出，可以基于以上知识来构造一个三层的神经网络，然后选取合适的小波基，将小波基进行线性加权叠加求和从而逼近非线性函数，即公式(5)。小波神经网络的结构参见图1。

图1 小波神经网络结构

2 ACO 算法训练神经网络

蚁群算法是一种仿生进化算法，是在20世纪90年代初提出的，该算法是一种启发式搜索方法，具有离散性、并行性、鲁棒性、正反馈性等特点。和其他的模拟进化算法，如粒子群算法、人工蜂群算法等进行比较，这些算法的共同点都是通过在进化过程中对候选解组成的群体进行最优解的寻找［1，2］。

蚂蚁、白蚁、蜜蜂、黄蜂等社会性昆虫的个体行为是很简单的，但是一个群体(colony)的集体行为却是复杂的。它们可以通过跟随其它个体所留下的踪迹等简单的相互作用方式，来对困难的问题进行求解，比如，可以从众多的路径之中选择出通往食物源的一条最短的路径。这种由一组社会昆虫表现出的集体行为称为群体智能(Swarm Intelligence)。

群体智能具有灵活性、容错性、自组织特征，这些特点使得一个群体能够适应变化的环境，在一个或多个个体失败的情况下，群体能够仍然完成任务，并且其行动既没有集中控制也没有局部监视。ACO 算法有很重要的2 个特征，第一个特征是正反馈过程，它是蚂蚁在群体觅食的过程中表现出来的，在正反馈过程中，通过反馈机制的调节，系统的较优解会实现自身的增强，就会使得问题的求解趋于全局最优，第二个特征是能够实现分布式并行计算，能同时在全局中的很多点上搜索解，避免使算法陷入局部最优［4，5］。

本文利用ACO 算法的全局最优化特征及ACO 的启发式寻优特征来训练神经网络的权值，从而达到智能寻优神经网络模型的目的［6－8］。对神经网络进行训练要基于如下原理:首先设定神经网络中有M 个参数，包括所有的权值参数和所有的阈值参数;然后对所有参数进行排序，对参数Pi(1 ≤i ≤M)，将属于该参数的所有的可能值进行组合，形成一个参数集合ΩPi，接下来定义一个蚂蚁群体，该群体具有一定数量;让蚂蚁群体从蚁巢开始出发，进行觅食;根据集合中各个元素的状态信息，蚂蚁从第1 个集合出发，从集合ΩPi(1 ≤i ≤M)按照随机的方式选取一个元素，同时调节所选取元素的信息素，当每一只蚂蚁都完成对集合中元素的选择以后，蚂蚁就到达了食物源，而后，按照前面所走过的路径再向蚁巢返回，调节相应元素的信息素，经过这样反复的迭代，蚂蚁最后实现最优参数的求解。

设有N 个蚂蚁，集合ΩPi(1 ≤i ≤M)有Dpi个元素，Pj(Ωpi)表示集合中第j 个元素的信息素。

蚁群进行搜索时，每一个蚂蚁在各个时间步骤之内只能选1 个元素，并且，在每一个时间步内，不同的蚂蚁所选择的元素的隶属集合是各不相同的。

此外，蚂蚁所选择的元素信息素的增量用符号I 表示，信息素的发挥用符号E 表示，如果E ＜0，则令E 恒等于0［9－11］。

3 基于ACO 算法的参数搜索步骤

第一步:初始化集合ΩPi(1 ≤i ≤M)中的每个元素的信息素Pj(Ωpi)，让N 只蚂蚁从蚁巢出发，每一只蚂蚁都执行第二步操作。

第二步:从集合1 开始，依据路径选择规则，每次让蚂蚁在每个集合中选择一个元素，然后给信息素一个增量I。

第三步:当所有蚂蚁对元素完成选择后，对每个元素的信息量进行调整，减去E。

第四步:从所有集合中对每一只蚂蚁进行元素的选择，之后执行第三步操作，沿着前面走过的路径向蚁巢折返，根据信息素调节的规则，对所选的元素的信息素提供一个增量。当所有的蚂蚁都返回蚁巢之后，转到第二步2。同时，对每一个时间步，都执行第三步操作。

信息素的调节需要遵循一定的规则:对每一只蚂蚁，当它从食物源返回蚁巢的期间内，根据如下公式(7)来实现信息素的调节。

在式(7)中，Ppl表示与元素pl 相对应的信息素，c 是一个常数，常数c 的作用是调节信息素的速度，e表示的是所进行的采样值的输出误差的最大值。

K 代表的是样本的个数，神经网络的实际输出用On表示，神经网络的期望输出用Oex表示。误差的大小反映信息素的水平，误差越小，相应信息素的增加的就越多。

步骤5:对上面的几个步骤进行重复，直到所有蚁群都寻找到最优的参数［6－9］。

4 仿真实验

为了对蚁群优化算法进行性能的评价，本论文进行了如下的仿真实验。实验网络选用前向神经网络，对公式(9)的函数进行逼近。蚁群规模为100，神经网络的输入层设定为1 个神经元，神经网络隐层设定为8 个神经元，输出层为1 个神经元，并与BP 算法、遗传算法、模拟退火算法进行性能比较，实验结果如表1所示。本文还针对不同噪声背景下的语音识别进行了仿真实验，实验数据是由女声数据组成，在实验室环境下录制，80 个人的录音，每人40 个词，每个词15 遍。本论文将实验室环境下所录制的语音视为纯净语音，然后将语音数据分别施加不同信噪比的白噪声、公交车内噪声、音乐噪声，形成5dB、10dB、15dB、20dB 信噪比的带噪信号。语音采样率为10KHz，其中前70 人的数据作为训练集，后10 人的数据作为测试集。每个语音文件分帧长度为30ms，帧移10ms。语音特征参数为提取每帧语音的归一化能量和每帧语音的12 维MFCC 系数，计算混合参数的一阶差分、二阶差分系数，这样一共构成39 维的特征参数矢量。实验结果如表2所示。

表1 4 种模型训练函数的比较

图2 不同信噪比条件下4 种模型的平均识别率比较

由表1、图2的数据可以看出，相比于BP 算法、遗传算法、模拟退火算法，算法在小波神经网络的训练方面具有较大的优势，相同的迭代次数，ACOMH 算法的均方误差最小。从语音识别的实验结果来看，ACOMH 算法训练的小波神经网络具有更强的抗噪识别性能，是一种有效的抗噪语音识别方法。

5 结 语

本文对ACO 算法的原理和小波神经网络结构及原理进行了研究，应用蚁群优化算法来训练小波神经网络，对其基本原理和步骤进行了研究，与遗传算法、模拟退火算法以及BP 算法进行了实验对比，实验仿真结果表明，ACO 算法具有更快的收敛速度，获得的均方误差更小，在算法的收敛上具有更加明显的优势和稳定性，对于抗噪声语音识别来说，该算法训练的神经网络也具有更优越的识别性能。

［1］Amr Badr，Ahmed Fahmy.A Proof of Convergence for Ant Algorithms［J］.Information Sciences.2004，16:267－279.

［2］GUO ZhiHua，CAO HuaiXin，CHEN ZhengLi＆YIN JunCheng.Operational properties and matrix representations of quantum measures［J］.Chinese Science Bulletin，2011，56(16):1671－1678.

［3］Dahl G E，Ranzato M，Mohamed A，et al.Phone recognition with the mean－covariance restricted Boltzmann machine［J］.Advances in Neural Information Processing Systems，2010，23:469－477.

［4］Thomas Stutzle，Marco Dorigo.A Short Convergence Proof for a Class of Ant Colony 0ptimization Algorithms［J］.IEEE Trans on Evolutionary Computation.2002，6(4):358－365.

［5］宋崇智，王璐.基于蚁群优化算法的神经网络训练的研究［J］.自动化与仪表，2006(5):10－12.

［6］张航，罗熊.蚁群优化算法的研究现状及研究展望［J］.信息控制，2004，33(3):3l8－324.

［7］詹士昌，徐婕，吴俊.蚁群算法中有关算法参数的最优组合选择［J］.科技通报，2003，19(5):29－34.

［8］Maniezzo V，Colorni A，Dorigo M.The Ant System Applied to the Quadratic Assignment Problem［J］.1EEE Trans on Knowledge and Data Engineering，1999，l1(5):769－778.

［9］W.J.Gutjahr.A graph—based ant system and its convergence［J］.Future Generation Computer System，2000，16:837－888.

［10］胡娟，王厂庆，韩伟.蚁群算法及其实现方法研究［J］.计算机仿真，2004，21(7):110－114.

［11］钱晓山.一种改进的混沌粒子群优化混合算法［J］.应用科技.2012，39(1):5－8.