任意四边形剖分二维MT有限元正演模拟

毕 武，刘 云

（1．乌鲁木齐金维图文信息科技有限公司，乌鲁木齐 830091；2．新疆地矿局物化探大队，昌吉 831100；3．中国科学院地球化学研究所，贵阳 550002）

任意四边形剖分二维MT有限元正演模拟

毕 武1，2，刘 云3

（1．乌鲁木齐金维图文信息科技有限公司，乌鲁木齐 830091；2．新疆地矿局物化探大队，昌吉 831100；3．中国科学院地球化学研究所，贵阳 550002）

为了模拟实际的起伏地形，在前人研究的基础上，单元网格设计为任意四边形网格，单元内的场值双线性变化，采用了高斯数值积分法计算单元系数矩阵，并给出二维大地电场的辅助场表达式。通过模型算例表明，模拟结果与解析解的均方误差在1%以内，地形模型与前人的模拟结果相吻合。分析对比了两个不同坡度模型对视电阻率和相位的影响。采用任意四边形网格剖分法，降低了编程难度，可以方便地适应野外地形的起伏变化。

大地电磁；起伏地形；任意四边形网格；有限单元法

0 引言

大地电磁测深法（MT）的野外观测，往往在地形条件复杂的山区进行，起伏地形对于电磁场的影响非常大，有必要研究带地形的 MT数值模拟技术。

Wannamaker［1］、陈小斌［2］等采用自适应地形的三角网格剖分，双线性插值有限元数值模拟起伏地形影响。刘云［3－4］等采用自适应地形的曲边四边形网格剖分双二次插值方法，以及采用四边形结合三角形剖分的电导率连续变化的二维有限元模拟技术，对起伏地形的大地电磁法观测取得较好的效果。

作者在前人研究基础上，导出了任意四边形单元剖分、双线性插值的大地电磁二维数值计算方法。实现了以高斯数值积分计算单元系数矩阵以及辅助场和视电阻率的计算。

1 变分问题

选择如图1所示的坐标系，假定地下电性结构是二维的，取走向为z轴，那么三维地电模型可以简化为二维地电模型来进行处理。经过推导与 MT二维边值问题相应的变分问题为［11］：

其中 ：σ为介质电导率；μ为磁导率取为常数μ≈μ0＝4π×10－7；ω是电磁波的角频率；k是传播系数，k

2 有限单元法

2．1 区域剖分

对于形如图1所示的地形，采用四边形网格剖分，可在地面各点加入高程信息形成二维起伏地形。由于网格单元不再是常规的矩形单元，将不满足矩形剖分的公式，需导出任意四边形单元线性插值场分量计算方法。公式（1）离散之后为

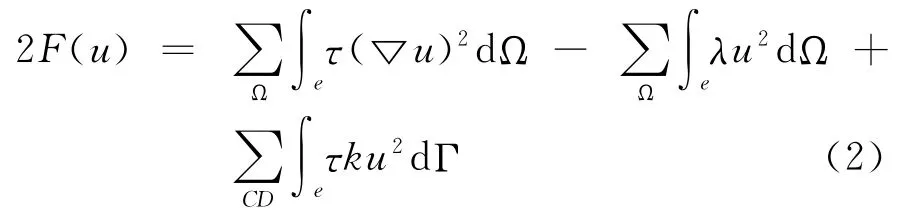
图1 区域剖分示意图Fig．1 Division of region with FEM grids

在图1中，加入高程信息的计算公式为

其中：Yp是点p的高程数据（水平地形条件下Yp＝0，正地形时Yp＞0，负地形Yp＜0）；yi是水平地形下，y方向上第i个节点的y坐标；Y为水平条件下y方向的最大距离；N为y方向上剖分的网格节点个数。带入此公式运算之后，Yi即为y方向上第i个节点添加了高程信息之后的y坐标。这样高程便以一个较小的变化依次加入到y方向上的节点中［13］。对于TE模式，空气层中高程信息的加入类比于TM模式中对于地下网格的处理。

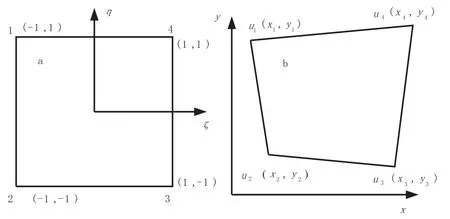
图2 任意四边形单元Fig．2 Arbitrary quadrilateral element

2．2 单元分析

单元如图2所示。

双线性插值的形函数为

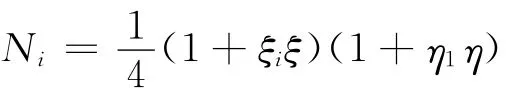
其中ξi、ηi是点i（i＝1，2，3，4）的坐标。图2（a）所示的二维等参单元分别表示场值u和坐标x、y为：

将每个单元的矩阵按照单元和节点编号带入总体矩阵中，采用变带宽存储总体矩阵。F（u）＝UTKU，令其变分为0，得到KU＝0，带入上边界条件之后，解方程组，就可以得到各个节点的U值。

当网格较多时，对所有单元系数均使用高斯数值积分计算是比较费时的。考虑到剖分区域时大量的单元是矩形的，只有涉及地形的部分是四边形的，所以在单元分析的程序部分，加入一个条件判断，如果该单元是矩形，那么直接使用常规系数矩阵，若不是矩形单元，则使用上述方法计算系数矩阵。下面给出矩形线性插值的单元系数矩阵：

3 计算视电阻率和阻抗相位

3．1 辅助场的求取

使用四边形剖分，根据单元分析中的推导有：

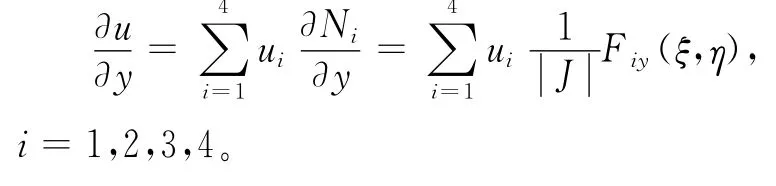
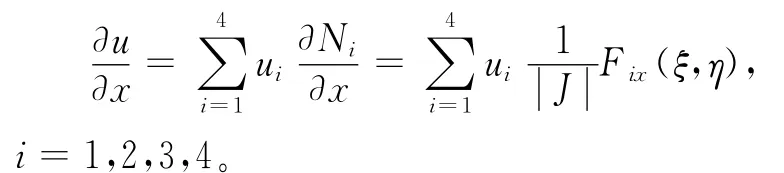
3．2 视电阻率和阻抗相位的计算

在TE模式中，由于磁场的连续性，起伏地形条件下Ez和Hx均可测得，所以起伏地形TE模式的视电阻率和阻抗相位的定义与水平地形条件相同。

在TM模式中，磁场分量Hz可以测得，但是电场在倾斜的地形线上不连续，电场水平分量Ex无法测得，只能测得沿地形线的El。根据矢量分解的定义，El分解为Ex和Ey分量［2］，即

此时，视电阻率和阻抗相位的定义为：

易知当水平地形时，由于Ey为零，同样可以应用该表达式。

4 模型算例

在以下模型算例中使用的网格剖分相同，研究区域两侧分别取18个稀疏网格，TE模式下，空气层取14个网格，地下介质剖分为56个网格（y方向），求解区域x方向剖分的网格数取为测点数。

4．1 层状模型

模型如图3所示，水平层状KH型地电模型（4层），模型参数为：第一层ρ1＝20Ω·m，h1＝200 m；第二层ρ2＝200 Ω·m，h2＝1 000 m；第三层ρ3＝20Ω·m，h3＝2 500 m；基底层ρ4＝200Ω·m。地面测线长4 km，测点间距100 m，一共41个测点，频率范围为1 000 Hz～0．01 Hz，对数等间隔采样，一共41个频点。

使用有限单元法求解，在CPU为T6600（2．2 GHz），内存2 GB的计算机上计算，TE模式每个频点的计算时间为0．58 s，TM模式每个频点的计算时间为0．31 s。

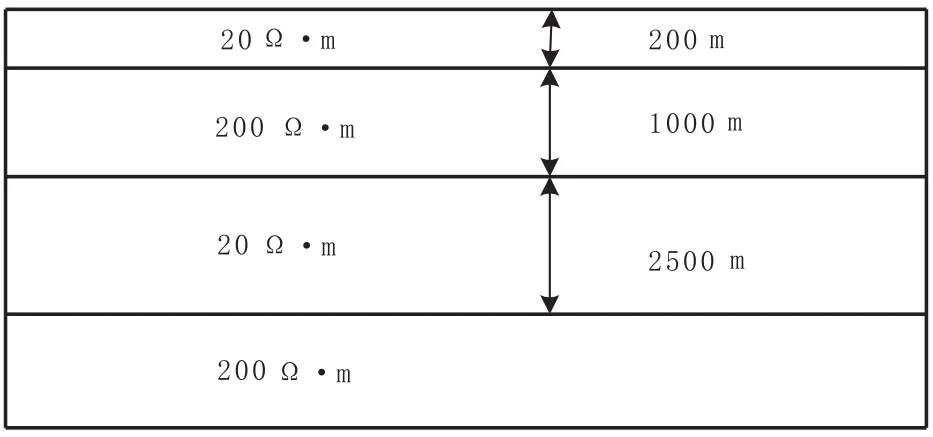
图3 KH型地电模型Fig．3 Schematic of KH－type geoelectric model

取21号测点（测区中间）的数值解与该模型的解析解进行对比，如图4所示。

图4 KH型模型解析解数值解对比Fig．4 Comparison between analytical and numerical solutions by FEM

从图4中可以看到，数值解与解析解是基本重合的。通过计算其他模型与解析解对比发现，视电阻率和阻抗相位值的均方误差均小于1%。

4．2 梯形山模型

模型具体参数如图5所示，该模型引自文献［1］，测线水平宽度为4 km，测点距50 m，梯形山位于测区中心，背景电阻率ρ＝100Ω·m，求解的频率为2 Hz。

模拟结果如图6所示。

对比文献［1］中的结果，可以看出响应曲线的形态和值的大小是一致的。

4．3 斜坡地形1

图5 梯形山模型Fig．5 Trapezoidal hill

如图7所示，测线水平宽度为6 km，测点距50 m，共121个测点，斜坡高度为1．2 km，斜坡跨度为3．0 km，斜坡坡度为23．6°，背景电阻率ρ＝100Ω·m，求解的频率为1 Hz。模拟结果的视电阻率以及相位曲线，如图8所示。

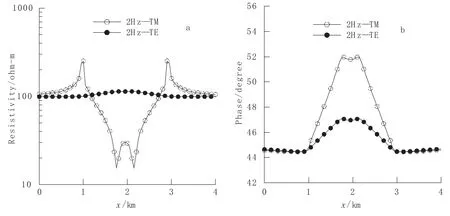
图6 梯形山模型2 Hz TE，TM模式视电阻率以及相位响应曲线Fig．6 TE／TM response curve at 2Hz of trapezoidal hill

对比文献［1，12］中的模拟结果，视电阻率以及相位的响应曲线基本一致。

从梯形山模型以及斜坡模型的数值模拟结果可以看出，TM模式的视电阻率以及相位受地形的影响较为严重，而TE模式受到影响相对较小。

4．4 斜坡地形2

下面通过对两个不同坡度模型的模拟结果，对比不同频率以及坡度对大地电磁场测量的影响。

如图9所示，斜坡高度为2 km，斜坡跨度为3．0 km，斜坡坡度为41．8°，背景电阻率ρ＝100Ω·m，测量参数与4．3中一致，求解频率为0．1 Hz、1 Hz以及10 Hz。

两个坡度的视电阻率模拟结果如图10所示。

图8 斜坡模型10 Hz的TE，TM响应曲线Fig．8 TE／TM response curve at 10Hz of the ramp terrain model

图9 斜坡地形2Fig．9 Ramp terrain model 2

在图10（a）、（b）中，为了突出对视电阻率的影响，纵轴为线性变化，从模拟结果可以看出，低频时，TE模式受到的影响较小，越往高频，受到地形的影响越大，同时对比图（a）、（b）两图可以看出，斜坡2视电阻率受到的影响相对于斜坡1更大，说明坡度越大，对视电阻率的影响越大。图10（c）、（d）中纵轴为对数值，可以看出TM模式下，视电阻率在低频和高频均受到很大的影响，并且坡度越大，其视电阻率畸变越大。在远离坡脚1 km处，高频视电阻率趋于背景电阻率，而低频视电阻率依然受到斜坡的影响。

从图11中发现，斜坡对于TE模式相位的影响相对较小，对TM模式的影响较大，并且坡度越大，阻抗相位的率畸变越大。在远离坡脚1 km处，高频的阻抗相位趋于45°，而低频的阻抗相位依然受到斜坡的影响。这些影响特点，与斜坡对视电阻率的影响是一致的。

5 结论

使用任意四边形剖分方式可以方便的适应地形变化，同时因为总体网格的剖分是采用矩形剖分，所以构建网格的部分是比较简单的。通过对层状模型以及地形模型的模拟，验证了方法的正确性。对斜坡地形，TE模式视电阻率和相位受地形影响较小，TM模式受到的影响较大。坡脚越大，视电阻率与阻抗相位畸变越大。远离斜坡测点的视电阻率和阻抗相位依然受到斜坡的影响，并且低频受到的影响更为严重。

图10 视电阻率曲线图Fig．10 Curve of apparent resistivity

图11 阻抗相位曲线图Fig．11 Curve of impedance phase

［1］ WANNAMAKER P E，STODT J A，RIJOFI L．Two－dimensional topographic responses in magnetotellurics modeled using finite elements［J］．Geophysics，1986，51（11）：2131－2144．

［2］ 陈小斌．MT二维正演计算中地形影响的研究［J］．石油地球物理勘探，2000，39（3）：112－120．

［3］ 刘云，王绪本．大地电磁二维自适应地形有限元正演模拟［J］．地震地质，2010，32（3）：382－391．

［4］ 刘云，王绪本．电性参数分块连续变化二维MT有限元数值模拟［J］．地球物理学报，2012，55（6）：2079－2086．

［5］ 朴化荣．电磁测深法原理［M］．北京：地质出版社，1990．

［6］ 王绪本，李永年，高永才．大地电磁测深二维地形影响及其校正方法研究［J］．物探化探计算技术，1999，21（4）：327－332．

［7］ 史明娟，徐世浙，刘斌．大地电磁二次函数插值的有限元法正演模拟［J］．地球物理学报，1997，40（3）：421－430．

［8］ 徐世浙，王庆乙，王军．用边界单元法模拟二维地形对大地电磁场的影响［J］．地球物理学报，1992，35（3）：380－388．

［9］ 徐世浙，于涛，李予国，等．电导率分块连续变化的二维MT有限元模拟（Ⅰ）［J］．高校地质学报，1995，1（2）：65－73．

［10］李予国，徐世浙，刘斌，等．电导率分块连续变化的二维MT有限元模拟（Ⅱ）［J］．高校地质学报，1996，2（4）：448－452．

［11］徐世浙．地球物理中的有限单元法［M］．北京：科学出版社，1994．

［12］尤淼．电性参数分块连续的大地电磁二维有限元数值模拟［D］．成都：成都理工大学，2011．

［13］吕玉增，阮百尧．复杂地形条件下四面体剖分电阻率三维有限元数值模拟［J］．地球物理学进展，2006，21（4）：1302－1308．

［14］彭国伦．Fortran 95程序设计（第一版）［M］．北京：中国电力出版社，2002．

［15］徐士良．计算机常用算法（第二版）［M］．北京：清华大学出版社，1995．

Two－dimensional magnetotelluric forward modeling by arbitrary quadrilateral finite element method

BI Wu1，2，LIU Yun3
（1．Urumqi Jinwei Map－character Information And Science＆Technology Co．Ltd，Urumqi 830091，China；2．Geophysical and Geochemical Party，Xinjiang Bureau of Geology and Mineral Resource Exploration and Development，Changji 831100，China；3．Institute of Geochemistry Chinese Academy of Sciences，Guiyang 550002，China）

In order to easily model topography in field work，on the basis of predecessors＇achievements，the arbitrary quadrilateral element grid was used in the finite element method（FEM），and the electromagnetic field of models were designed to bilinear variation within each quadrilateral element in our numeric modeling．We deduced the specific formula to calculate the unit coefficient matrix by Gaussian numerical integral and the expression of the auxiliary field when using arbitrary quadratic element．Model calculation shows that the mean square error between the simulation results with the analytical solution is less than 1 percent，and the results of terrain model is consistent with the one of other scholar＇s．Through modeling of two ramp terrain modes with different pitch，comparing and analyzing the effect of the apparent resistivity and the phase．Due to the use of arbitrary quadrilateral element grid，the difficulty of programing was reduced，forward modeling can be more easily adapt to the topography variation．

MT；topography；arbitrary quadratic element；FEM

P 631．3＋25

A

10．3969／j．issn．1001-1749．2014．05．02

1001-1749（2014）05-0521-08

2014-01-17 改回日期：2014-07-17

毕武（1970－），男，高级工程师，主要从事物化探数据处理解释等方面的研究工作，E-mail：382280581＠qq．com。