一类二阶变系数线性齐次微分方程的通解

张玉兰，曹亚萍

（南京铁道职业技术学院社科部，江苏南京 210015）

一类二阶变系数线性齐次微分方程的通解

张玉兰，曹亚萍

（南京铁道职业技术学院社科部，江苏南京 210015）

结合文献［1］中的结论（见引理3）进行推导，得出方程y″+P（x）y′+Q（x）y=f（x）所对应的齐次方程相对应的Riccati方程特解的求法，在此基础上，得出方程y″+P（x）y′+Q（x）y=0对应的通解。

二阶变系数微分方程；Riccati方程；特解；通解

二阶线性齐次微分方程在微分方程理论和应用上都占有重要位置。关于常系数线性微分方程的通解结构，一般的文献中有完美的结论，但对于二阶线性变系数微分方程却无通用的求解方法［1-7］。笔者结合文献［1］中的结论（见引理3）进行推导，得出了方程

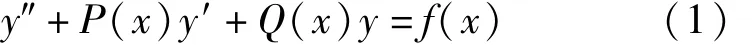
所对应的齐次方程

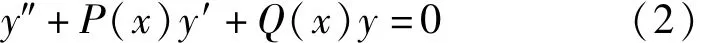
相对应的Riccati方程特解的求法。

1 引 理

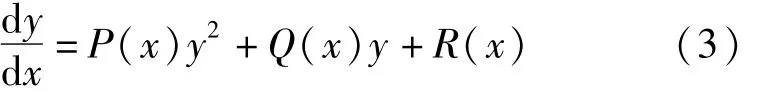
法国数学家刘维尔（Liouville）在1841年证明了著名的黎卡提（Riccati）方程一般是不可积的，即不能用初等积分法求解。相关文献［2-4］给出了待定系数满足定理条件时Riccati方程的通积分。如

引理1对于方程（3），若系数满足

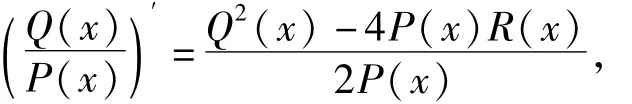
则可积，且其通积分为

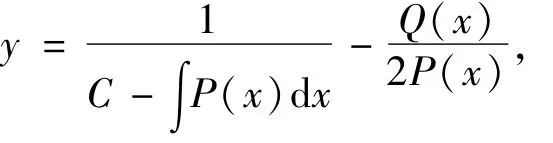
其中，C为常数［2］。

文献［5］给出了方程（1）在得知Riccati方程

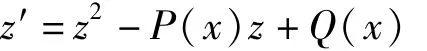
的1个特解z=z（x）时的通解积分公式（见引理2）。

引理2设P（x），Q（x）及f（x）是连续函数，且z=z（x）是Riccati方程

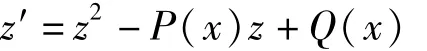
的1个特解，则方程（1）可积且其通积分为

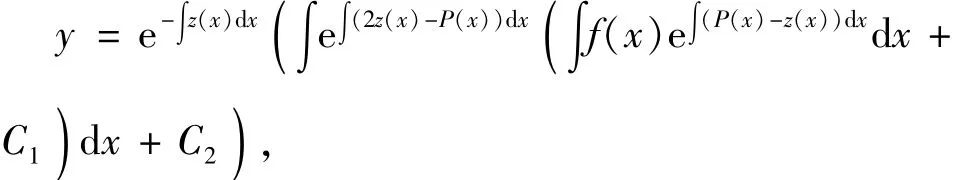
其中，C1，C2为常数。

引理3设P（x），Q（x）及f（x）是连续函数，且

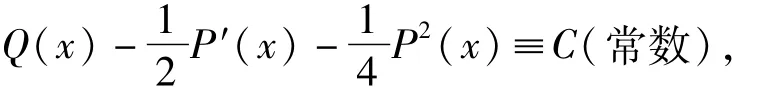
则方程（1）的通解可求出。

2 定理及其证明

首先，考察方程（1）对应的Riccati方程

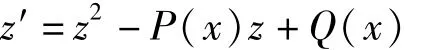
在

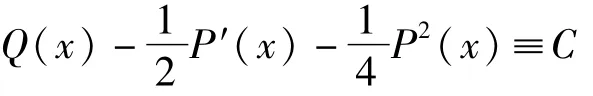
下的特解，在此基础上，得出方程（2）对应的通解。

定理1若

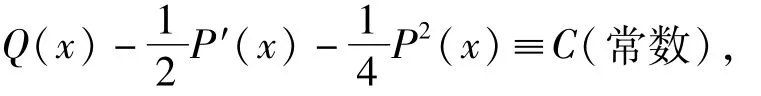
则方程（1）对应的Riccati方程

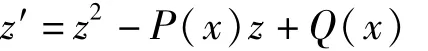
的特解是

1）当C=0时，

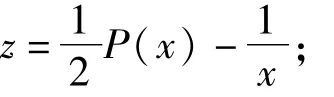
2）当C＞0时，

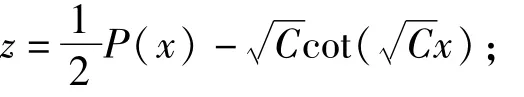
3）当C＜0时，

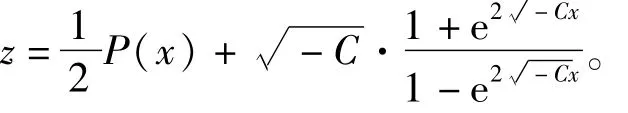
证明 1）当C=0时，

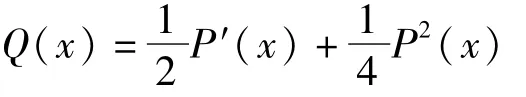
所以

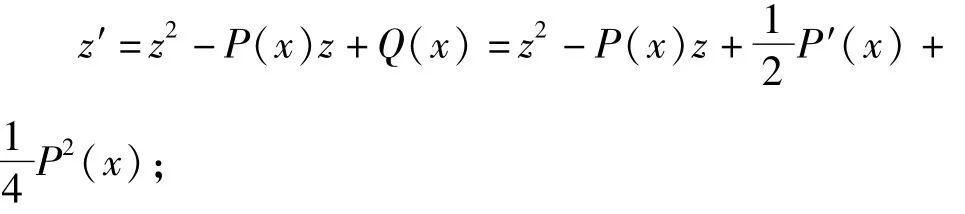
令

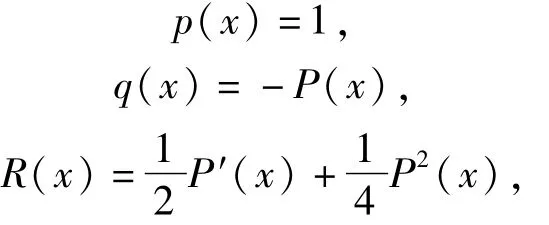
所以

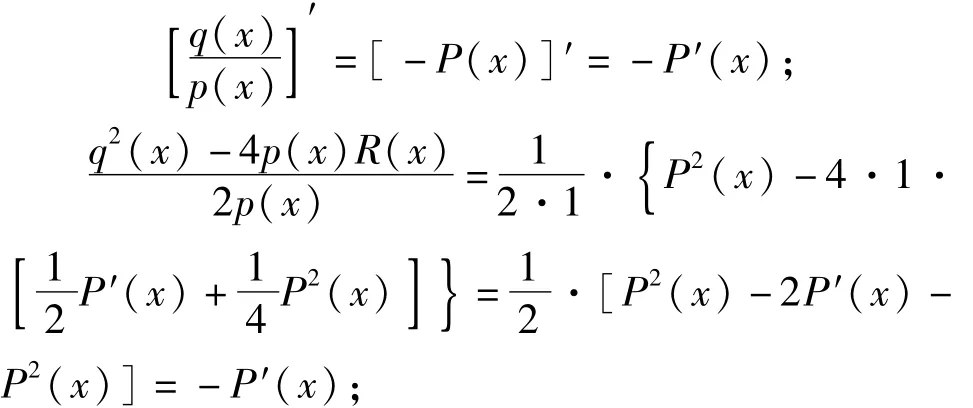
即

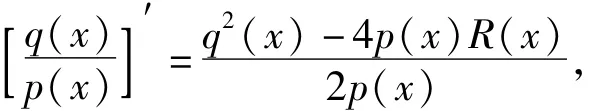
亦即Riccati方程

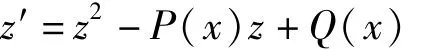
的系数满足引理1的条件，故其可积且其通积分为

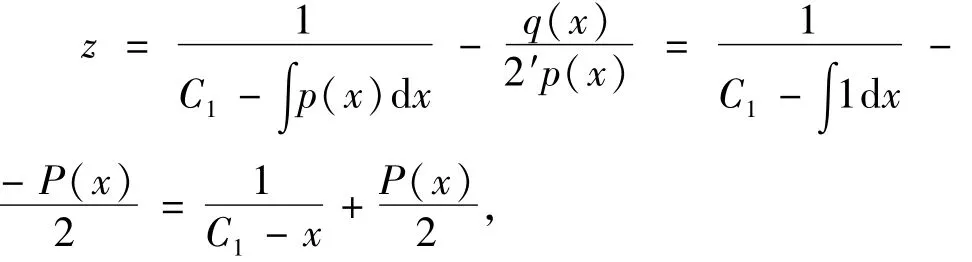
其中，C1为常数。当C1=0时，得其特解，即

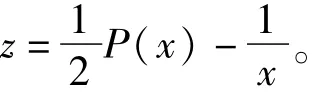
而当C≠0时，将

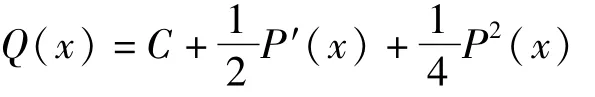
代入Riccati方程

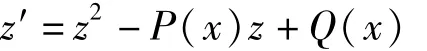
得

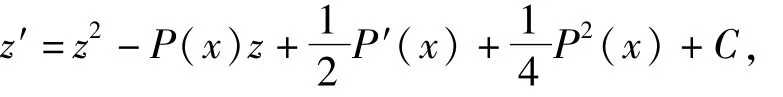
即

令

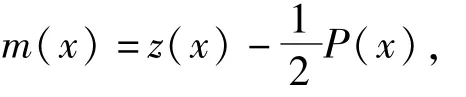
则方程（4）可化为

即

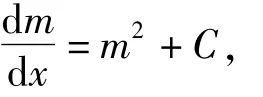
整理得

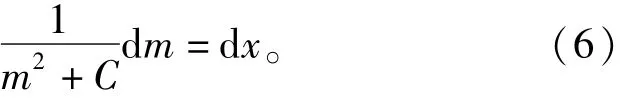
当C＞0时，方程（6）即为

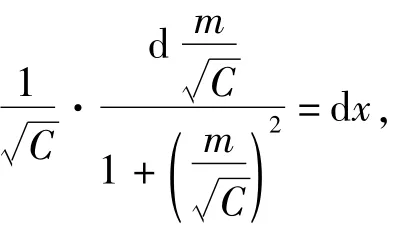
两边积分得

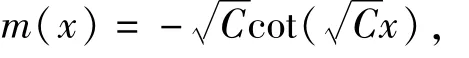
从而得方程（5）的1个特解为

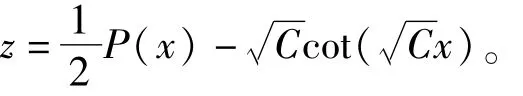
当C＜0时，方程（6）即为

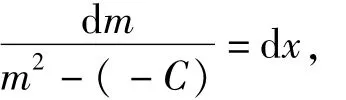
亦即

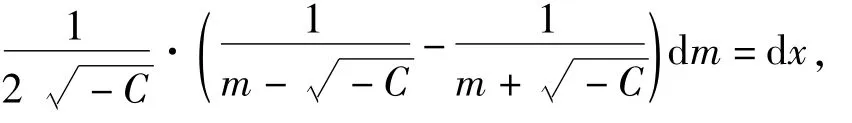
两边积分得

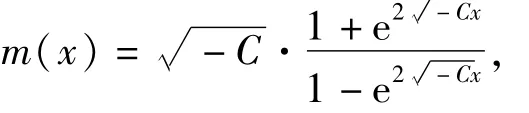
从而得方程（5）的1个特解为

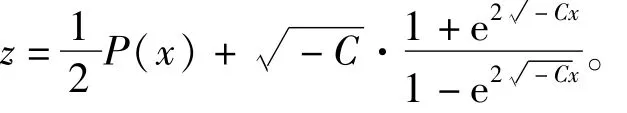
定理2设P（x），Q（x）及f（x）是连续函数，且

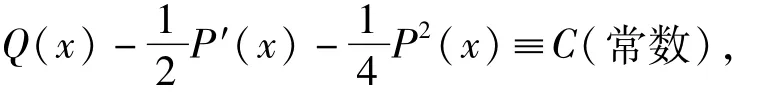
则方程（2）的通解为

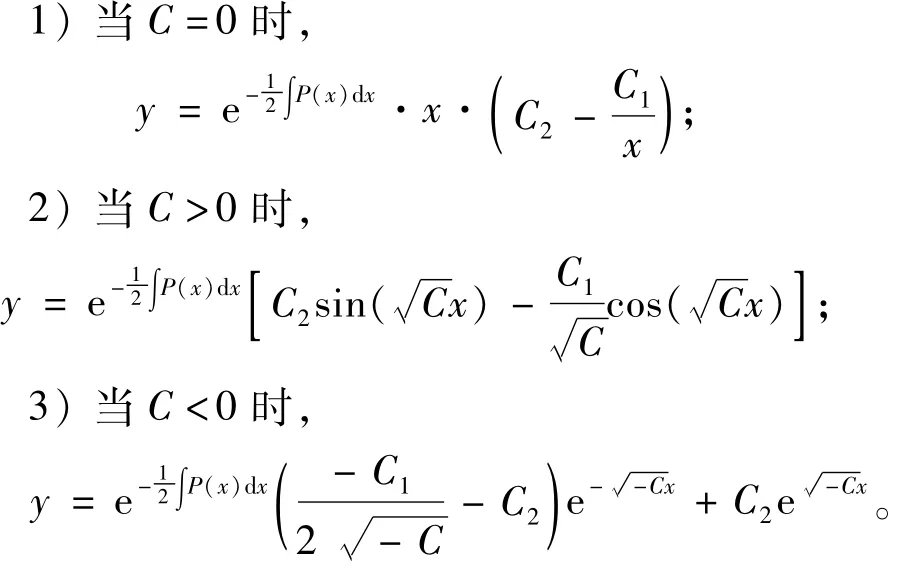
证明因为方程（2）是方程（1）的齐次方程，所以由引理2得方程（2）的通解为

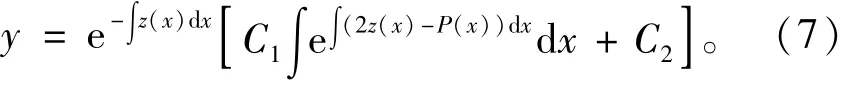
再将定理1的3个结果代入方程（7）即可。下面仅以C＜0为例，其他2种情况类似可得。

当C＜0时，

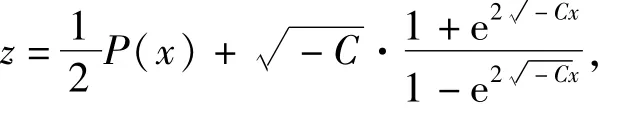
所以

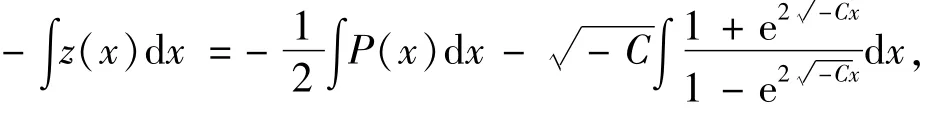
其中，

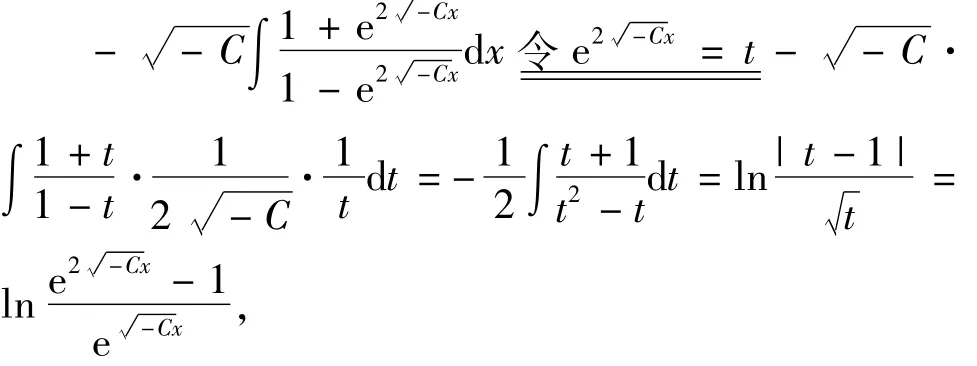
所以

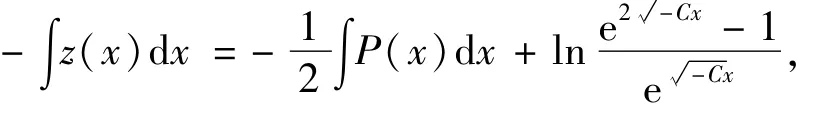
故

又因为

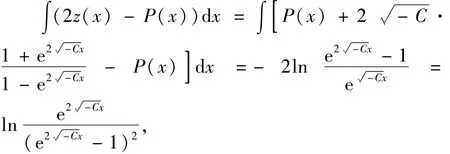
所以

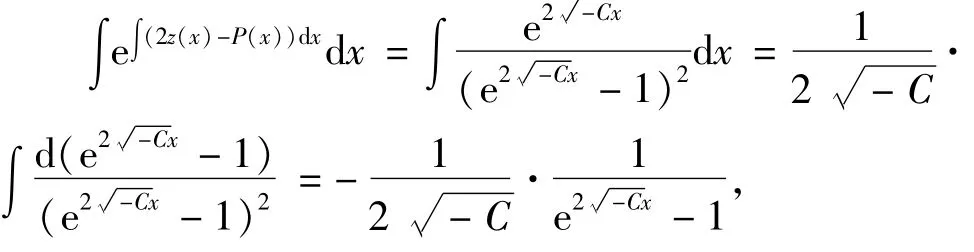
从而可得方程（2）的通解为

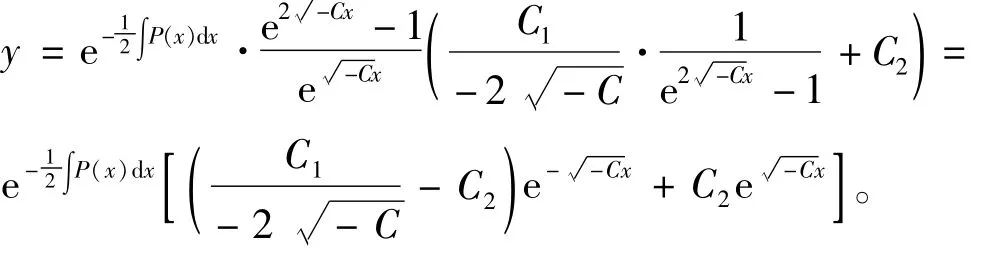
［1］罗正平，陈仲.微分方程［M］.南京：南京大学出版社，1987：124.

［2］王玉萍，卢琨，史胜楠.Riccati方程的可积条件及通积分［J］.陕西科技大学学报，2007（25）：136-138.

［3］庞建华.Riccati方程的一些新的可积条件［J］.广西工学院学报，2008（2）：89-92.

［4］曹友娣，刘玉彬.一类二阶变系数微分方程的解［J］.惠州学院学报：自然科学版，2010（3）：19-25.

［5］敏志奇.一类变系数微分方程通解公式的求法［J］.高等数学研究，2005（3）：16-17.

［6］王高雄，周之铭，朱恩铭，等.常微分方程［M］.2版.北京：高等教育出版社，2000：166-180.

［7］张玉兰.二阶变系数线性齐次微分方程的通解［J］.长沙大学学报：自然科学版，2013（27）：1-3.

〔责任编辑：卢 蕊〕

General solution to a class of second order variable coefficient linear homogeneous differential equation

ZHANG Yu-lan，CAO Ya-ping
（Social Science Department，Nanjing Institute of Railway Technology，Nanjing 210015，China）

This thesis focuses on the general solution to a class of second order variable coefficient linear homogeneous differential equation.Combining a conclusion in Document［1］（see Lemma 3）deduction ismade to obtain a particular solution method to the corresponding Riccati equation in informity with the homogeneous equation，on which basis，a corresponding general solution to the equation is achieved.

second ordinary differential equations；Riccati equation；particular solution；general solution

O172.1

C

1008-8148（2014）01-0045-03

2013-06-22

张玉兰（1982—），女，江苏盐城人，讲师，硕士，主要从事运筹学与控制论研究；曹亚萍（1961—），女，江苏常州人，副教授，主要从事高等数学教学研究。