局部主成分分析及其在软测量中的应用

邵伟明 田学民

(中国石油大学(华东)信息与控制工程学院,山东 青岛 266580)

局部主成分分析及其在软测量中的应用

邵伟明 田学民

(中国石油大学(华东)信息与控制工程学院,山东 青岛 266580)

在软测量建模中,局部学习策略是解决过程时变特性及非线性的有效途径。为提高模型预报精度,提出了一种基于局部主成分分析的在线软测量建模方法。该方法采用主成分建立局部模型,同时考虑变量间的相关性以及映射关系构建局部模型的选择准则。此外,为了提高在线计算效率、降低对存储设备的要求,提出了一种基于预报残差方差和均值的冗余模型判别方法。在某连续搅拌反应器上的仿真结果验证了该方法的有效性。

软测量 局部学习 主成分分析(PCA) 冗余模型 连续搅拌反应器(CSTR)

0 引言

基于数据驱动的软测量建模方法,如主成分分析[1]、偏最小二乘[2]、支持向量机[3]等及其递推方法[4-7],获得了广泛的应用。但递推方法无法及时跟踪主导变量的突变,且单一模型难以处理过程的非线性。而局部学习采用“分而治之”的思想,能有效解决上述问题。在局部学习中,如何选择合适的局部模型是关键问题。即时学习通常根据样本间的欧式距离及夹角,选择若干相似样本构建局部模型[8-11],但这类方法未考虑变量间的相关性。文献[12]提出了一种基于相关性的局部学习方法(CoJIT),即采用PCA计算每个子模型对新获取样本的Q及T2统计量,但其忽略了变量间的映射关系。

本文首先将数据库分成若干子集,采用PCA计算其输入空间的负荷向量及主成分。其中,主成分用于建立局部模型；而负荷向量用于衡量新样本到输入空间的距离,并结合预报残差构建模型选择准则。此外,为降低在线计算负担及模型数量,提出了一种淘汰冗余模型的策略。最后通过仿真分析验证方法的有效性。

1 模型选择与冗余模型判别

1.1 主成分分析

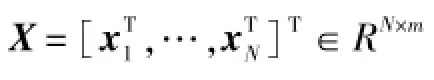
由于主成分T的各列线性无关且维数低,因此选择主成分建立局部模型,既能消除数据间的共线性、抑制噪声的影响,又能减少计算量。本文建立主成分T而非原始数据X与输出Y间的映射关系,即:

此外,对某样本x0构造Q及HotellingT2统计量,用于衡量x0与X的相关性:

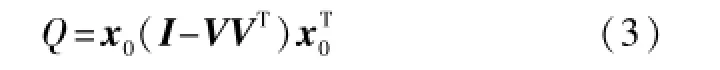
式中:Q为x0到X子空间的距离；tk为x0的第k个主成分。

1.2 局部模型选择

合理选择局部模型是提高局部学习预报精度的关键。在CoJIT[12]中,Q和T2的加权和[14-16]被用作选择局部模型的准则:

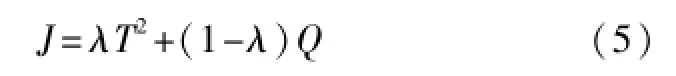
λ通常很小,起主要作用的是Q统计量,即新样本到局部模型子空间的距离。虽然J考虑了变量间的相关性,但忽略了辅助变量与主导变量间的映射关系,这可能导致较大的预报误差。不同的局部模型选择标准如图1所示。

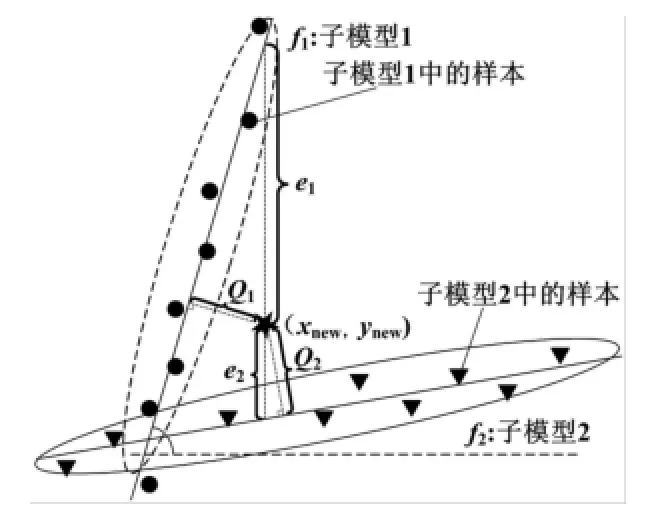
图1 不同的局部模型选择标准示意图Fig.1 Different selection criteria for local models

从图1可知,虽然新样本znew=[xnew,ynew]到子空间1的距离Q1＜Q2,但子模型1对znew的预报误差e1＞＞e2。因此,为提高模型的预报精度,应充分考虑变量间的映射关系,将预报残差作为主要的模型选择依据。然而过分追求预报误差最小化,可能由于数据分布及噪声等因素的影响导致过“过学习”现象,致使局部模型的推广能力不佳。鉴于上述两点,提出一种新的模型选择标准:

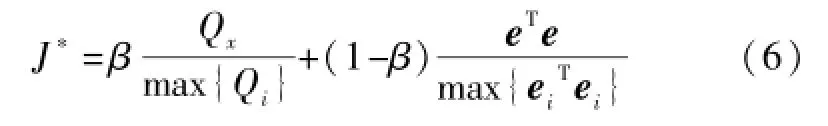
式中:e=f(xnew)-ynew为局部模型对新样本的预报误差；Qx为xnew到局部模型输入子空间的距离,用于抑制噪声的影响,避免“过学习”现象；Qi和ei分别为已存储的第i个局部模型对当前样本输入及输出变量的重构误差,用于归一化Qx及eTe。由于指标J*充分考虑了变量间的映射关系及相关性,因而较J能够更合理地选择局部模型。获取到新样本后,能够最小化指标J*的局部模型被选做描述过程当前状态的局部模型,并负责对后续未知样本作出预测。

此外，苏佩斯还认为，科学理论中还应当包括检验理论的实验统计过程与方法，因而也承认存在着因实验方法而产生的理论的层次结构。因此，在对理论模型的解读中，除了模型的层级系统外，还存在与之相对应的理论的层级系统。在科学理论的层级系统中，一个层次的理论通过与更低层次的理论形成正式联系而被赋予经验意义，并且不同层次理论之间的关系的统计或逻辑调查都可以以纯粹的、正式的、集合理论的方式进行。同时，理论模型的层级系统也通过层级性对每一层次的理论进行表征。因而以苏佩斯的理论为基点，我们不仅可以对理论和现象连接的问题进行纵向的解答，还可以对理论的拓展和形成问题展开横向的研究。

1.3 冗余模型判别

为考虑变量间的相关性,文献[12]采用滑动窗将过程状态分割为若干个局部区域,但这将产生过多的冗余局部模型。虽然根据子模型间的夹角准则选择性地存储模型,但未考虑数据的分布,易产生预报偏移。为了在合理划分局部区域的同时,避免对冗余局部模型的存储,本文在文献[12]的基础上,令模型间距为1,并提出一种基于预测残差方差及均值的冗余区域判别方法。基于聚类的多模型软测量方法往往无法较好地描述子模型间的过渡区域,但本文采用的子模型划分中,过度区域也有相应的子模型对其进行描述,因而在过度过程中不会出现较大的预报误差。

假设已经存储的第i个局部模型对第i个局部区域[Xi,Yi]以及新提取的局部区域[Xnew,Ynew]的预报误差分别记为Ei、Enew,i:

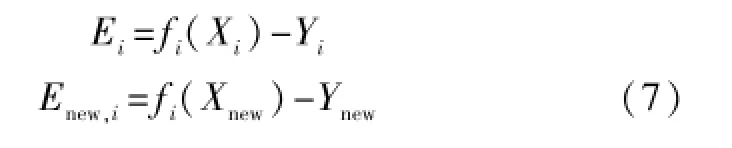
若:

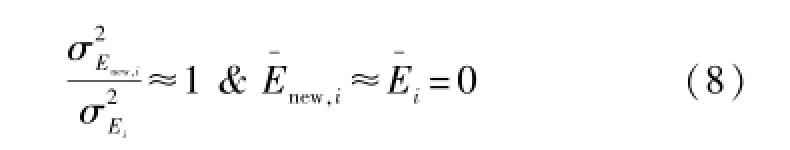
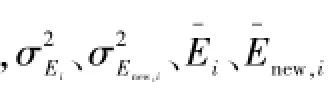
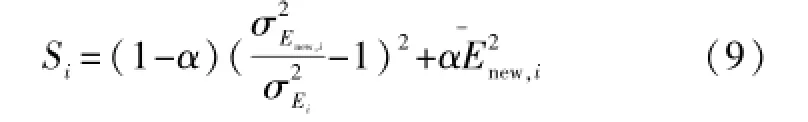
式中:α为均值所占的权重。

式中:为设定阈值,可用于调整预报精度与局部模型数量的关系。

2 在线软测量建模步骤

综合前文所述,所提出的软测量建模方法主要包括两个部分,即建立无冗余局部模型集合以及在线选择局部模型。

无冗余局部模型集合的建立步骤具体如下。

①初始化滑动时间窗长度SW、主成分个数p、残差均值的权重α以及阈值。

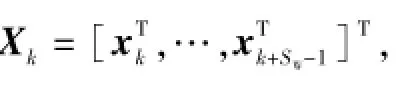
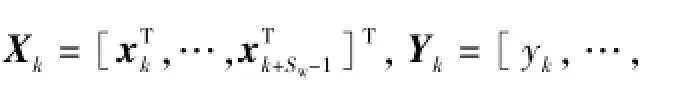
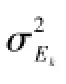
上述过程可离线完成,因此并不影响软测量模型在线运行的实时性。值得指出的是,对历史数据库划分完毕后,当在线获取到新的样本时,该过程将继续进行,以提取新的过程状态。

在线选择局部模型的步骤如下。

3 仿真研究

3.1 对象描述

连续搅拌反应器(continuous stirred-tank reactor, CSTR)是化工过程的重要设备之一,它通常是整个生产过程的核心。某非线性CSTR的系统结构如图2所示。物料A进入反应器内发生一级不可逆放热反应A→B,冷却剂通过夹套把反应过程中产生的热量带走。假设反应器内的温度T和浓度CA是均匀分布的,对该系统的反应器液位h和温度T分别实施串级控制。

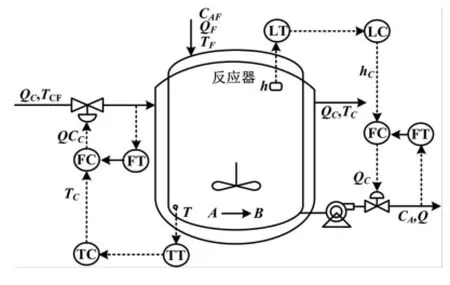
图2 某CSTR及其控制系统结构图Fig.2 The control system structure of CSTR

根据系统的物料平衡、能量平衡及化学反应机理,建立CSTR系统的机理模型为:

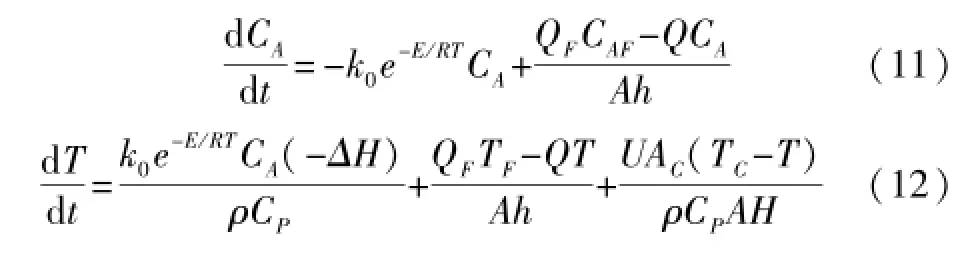
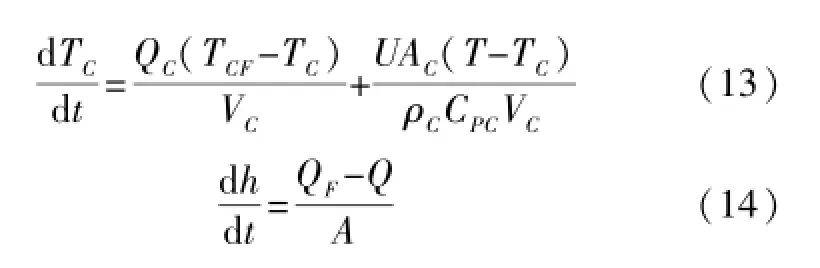
3.2 仿真结果

选择u=[T,h,Q,QC,QF]作为模型输入,反应后CA的浓度作为模型输出y。设输入变量的采样周期为0.1 min,输出变量的化验周期为6 h。为描述过程的动态特性,采用前一时刻的采样值对输入矩阵进行增广,建立动态软测量模型,即y(k)=f[u(k-1)、u(k-2)]。设定反应器催化剂活性随时间降低,且每隔54 d由人工恢复,频率因子k0的变化曲线如图3所示。

图3 频率因子k0变化曲线Fig.3 Variation of the frequency factork0

分别采用递推PLS(RPLS)、即时学习PLS(JITPLS)、基于相关性的即时学习(CoJIT)以及本文方法——在线局部PCA(online local PCA,OLPCA)建立上述CA浓度的软测量模型。在CoJIT以及OLPCA中,直接采用主成分回归建立局部模型。以均方根误差(root mean squares error,RMSE)、相对均方根误差(relative RMSE,RE)以及最大绝对误差(maximum absolute error, MAE)作为衡量不同方法预报精度的指标；将模型在线更新次数(upNum)和平均仿真时间作为软测量模型的效率指标。仿真所用计算机的配置为:操作系统为Windows XP；内存2 GB；CPU为Pentium Dual E5800 (3.2 GHz×2)；Matlab7.1版本。

上述方法的参数均通过粒子群优化(particle swarm optimization,PSO)算法以最小化RMSE为目标优化获得。在RPLS中,PLS的主成分个数为7,遗忘因子为0.98；在JIT-PLS中,相似样本个数为47,主成分个数为3；在CoJIT中,SW=25,模型更新阈值为0.18,λ=0.001,主成分个数为8；在本文提出的方法中,令=0、SW=25、*=0.005、β=0.01,主成分个数为8。4种方法的预报结果如图4所示。

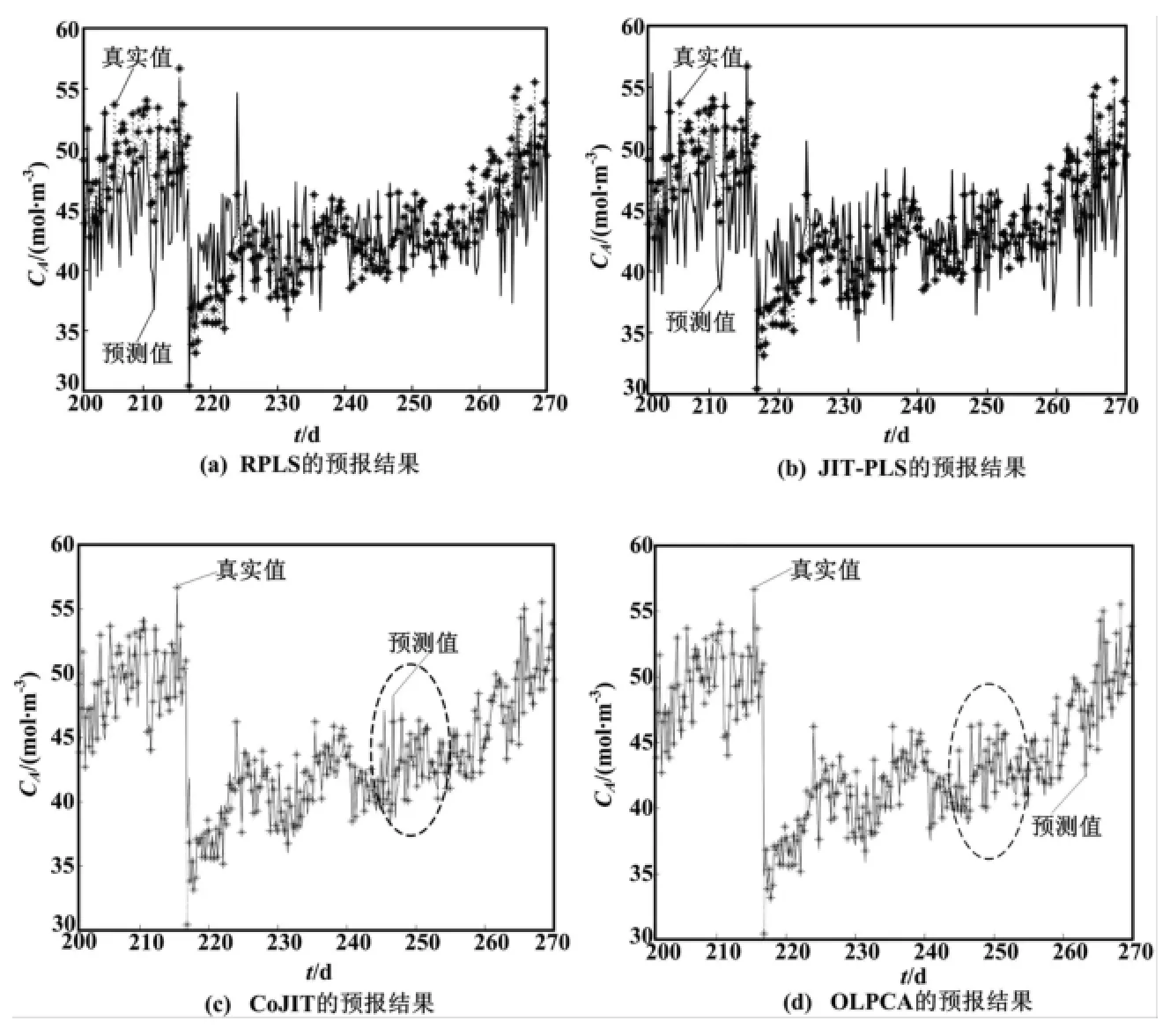
图4 不同方法对CA浓度的预报结果Fig.4 Predicted results of CAwith different methods

从图4可以看出,RPLS及JIT-PLS的预报效果比较差,其原因前文已经分析过了,在此不再赘述。而CoJIT和OLPCA,由于采用局部学习的策略,且考虑到了变量间的相关性,可有效处理过程的非线性及时变特性,因而能够较好地跟踪CA的变化。但在某些局部区域,OLPCA的预报精度较CoJIT有明显提高。将图4中椭圆标记的区域放大后如图5所示。此外,若将CoJIT与OLPCA的预报结果绘成散点图,可从整体上比较两者的预报精度,具体如图6所示。从图6可以看出,OLPCA的预报点较CoJIT更加紧凑地分布在对角线两侧,这表明本文方法的预报值与真实值更接近直线,即OLPCA具有更高的预报精度。

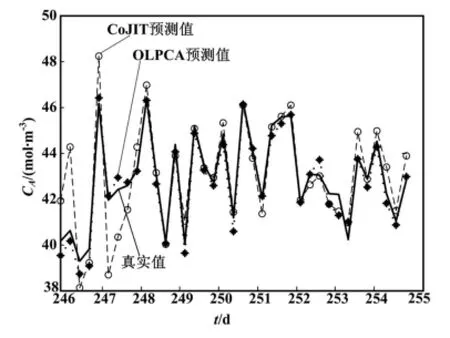
图5 椭圆区域的局部放大图Fig.5 Partial enlarged view of ellipse area

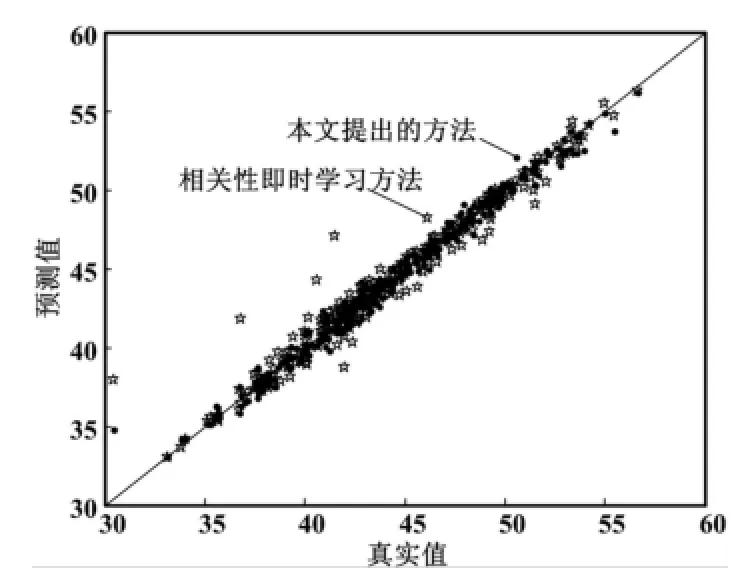
图6 CoJIT与OLPCA预报结果的散点图Fig.6 Scatter plots of the predicted results of CoJIT and OLPCA

为了定量比较各方法的性能,4种方法的预报误差及效率如表1所示。

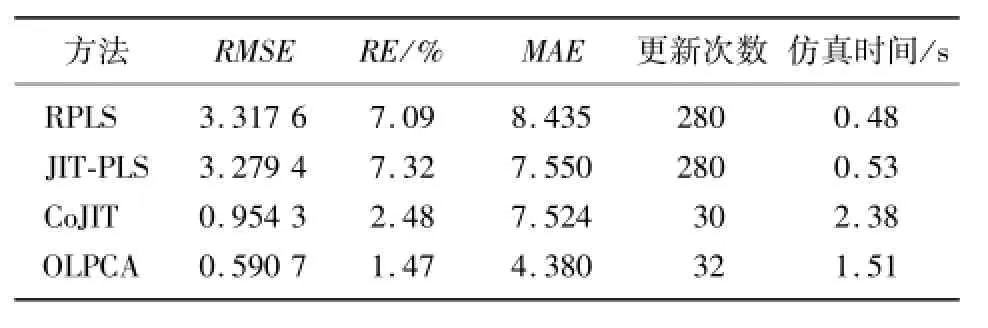
表1 不同方法的性能比较Tab.1 Performance comparison of different methods

从表1可以看出,虽然RPLS及JIT-PLS的在线运行效率较高,但其预报精度较低。而OLPCA较CoJIT能有效降低绝对误差、相对误差以及最大误差。同时由于OLPCA在建立局部模型时,采用已经获取到的主成分,因此其在线计算量也显著减少。OLPCA与CoJIT的区别仅在于采用不同的准则选择局部模型,这表明本文方法能够更合理地选择局部模型。

上述OLPCA的预报结果均在=0的条件下获得,此时共需要构建并存储1 056个局部模型。实际上,并不是对每个局部区域都需要建立子模型并将其存储。若采用本文提出的冗余区域判别方法,选择性地存储局部模型,设定不同的阈值时,预报精度(RMSE)与存储模型数量、平均在线运行时间的关系如表2所示(α=0.01)。

表2 与预报精度、模型数量以及在线运行时间的关系Tab.2 Relationships amongand predictive accuracy, model quantity and online operation time

表2 与预报精度、模型数量以及在线运行时间的关系Tab.2 Relationships amongand predictive accuracy, model quantity and online operation time

S-模型数量RMSECPU运行时间/s 0.0001 0560.590 70.601 0.0011 0260.590 70.591 0.0029830.595 30.560 0.0039420.594 40.550 0.0048850.595 60.505 0.0056770.598 20.406 0.0066240.604 20.387

模型数量与预报误差关系如图7所示。

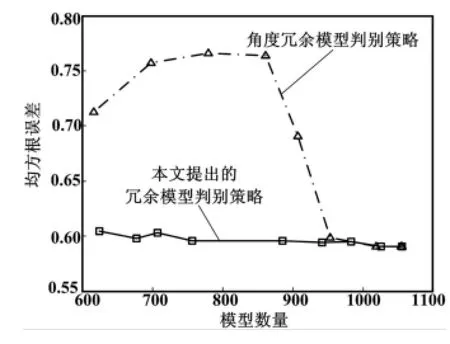
图7 模型数量与预报误差的关系Fig.7 Relationship between model quantity and predictive error

不难发现,在夹角准则中,当模型数量减少到一定数量时,模型预报精度迅速降低；而采用本文所提方法,虽然模型数量大幅度减少,但RMSE的上升趋势并不明显。这进一步表明了式(9)的有效性。

4 结束语

本文在局部学习框架下,提出一种基于主成分分析的软测量在线建模方法,主要解决两个问题:①如何在线合理选择局部模型；②如何在保证模型预报精度的前提下避免存储对冗余局部模型。对某连续搅拌反应器的仿真结果表明,在非线性及时变因素均存在的情况下,所提出的方法能够有效提高软测量模型的预报精度,并能充分降低在线计算负担以及存储负担。

[1] Ge Z Q,Song Z H.Semisupervised Bayesian method for soft sensor modeling with unlabeled data samples[J].AIChE Journal,2011, 57(8):2109-2118.

[2] Galicia H J,He Q P,Wang J.A reduced order soft sensor approach and its application to continuous digester[J].Journal of Process Control,2011,21(4):489-500.

[3] Yu J.A Bayesian inference based two-stage support vector regression framework for soft sensor development in batch bioprocesses[J]. Computer and Chemical Engineering,2012,41(1):134-144.

[4] Tang J,Yu W,Chai T Y,et al.On-line principal component analysis with application to process modelding[J].Neurocomputing,2012, 87(4):167-178.

[5] 邵伟明,田学民,王平.基于递推PLS核算法的软测量在线学习方法[J].化工学报,2012,63(9):2887-2891.

[6] Zhao Y P,Sun J G,Du Z H,et al.An improved recursive reduced least squares support regression[J].Neurocomputing,2012,87(1): 1-9.

[7] Liu Y,Wang H Q,Yu J,et al.Selective recursive kernel learning for online identification of nonlinear systems with NARX form[J]. Journal of Process Control,2010,20(2):181-194.

[8] Cheng C,Chiu M S.A new data-based methodology for nonlinear process modeling[J].Chemical Engineering Science,2004,59(13): 2801-2810.

[9] Chen K,Ji J,Wang H Q,et al.Adaptive local kernel-based learning for soft sensor modeling of nonlinear processes[J].Chemical Engineering Research and Design,2011,89(10):2117-2124.

[10] Liu Y,Gao Z L,Li P,et al.Just-in-time kernel learning with adaptive parameter selection for soft sensor modeling of batch processes[J]. Industrial and Engineering Chemistry Research,2012,51(11):4313-4327.

[11] 刘毅,王海清,李平.用于发酵过程在线建模的自适应局部最小二乘支持向量机回归方法[J].化工学报,2008,59(8):2052-2057.

[12] Fujiwara K,Kano M,Hasebe S,et al.Soft-sensor development using correlation-based just-in-time modeling[J].AIChE Journal,2009, 55(7):1754-1764.

[13] Shao W M,Tian X M.A soft sensor method based on integrated PCA [C]∥Proceedings of the 10th World Congress on Intelligent Control and Automation,July 6-8,2012,Beijing,China:4258-4263.

[14] Raich A,Cinar A.Statistical process monitoring and disturbance diagnosis in multivariable continuous processes[J].AIChE Journal, 1996,42(4):995-100.

[15] Johannesmeyer M,Seborg D E.Abnormal situation analysis using pattern recognition techniques and historical data[C]∥AIChE Annual Meeting,1995.

[16] 管秋,王万良,徐新黎,等.基于神经网络的污水处理指标软测量研究[J].环境污染与防治,2006,28(2):156-158.

Local Principle Component Analysis and Its Application in Soft Sensing

In soft sensing modeling,local learning strategy is an effective way to solve the time varying and nonlinear characteristics.In order to improve the accuracy of model prediction,the online soft sensing modeling method based on local principle component analysis is proposed. With this method,the local model is built by adopting principle component,and both the correlation relationship and mapping relationship between process variables are taken into consideration to provide appropriate selection criteria for building local model.In addition,to improve online compulational efficiency and reduce the demands for storage devices,the discriminant method of redundant models based on the residual variance and mean value of prediction is also proposed.The simulation result on certain continuous stirred-tank reactor(CSTR)verifies the effectiveness of this method.

Soft sensing Local learning Principle component aralysis(PCA) Redundant model Continuous stirred-tank reactor(CSTR)

TP301+.6

A

国家自然科学基金资助项目(编号:61273160);

中央高校基本科研业务费专项基金资助项目(编号:14CX06067A)。

修改稿收到日期:2013-07-19。

邵伟明(1986-),男,现为中国石油大学(华东)控制理论与控制工程专业在读博士研究生;主要从事软测量建模方面的研究。