全最小二乘法在姿态参数测量中的应用研究

曹平军 杨昌茂 张海波

(中船重工第七一〇研究所,湖北 宜昌 443000)

全最小二乘法在姿态参数测量中的应用研究

曹平军 杨昌茂 张海波

(中船重工第七一〇研究所,湖北 宜昌 443000)

针对由三轴GMR磁传感器构建的飞行体姿态测量系统,推导出地磁场与姿态角间的数学关系,分析了影响测量精度的因素。通过对比绝对最小二乘法和相对最小二乘法对磁传感器参数的修正结果,发现由于常规最小二乘法只考虑单一因素,导致由测量数据求出的磁场三分量和总磁场值仍存在较大的波动和误差。为解决这一问题,采用全最小二乘法对磁传感器参数进行整体修正。经无磁转台试验表明,该方法极大地提高了磁场和姿态角的测量精度。

GMR磁传感器 滚转角 俯仰角 姿态测量 相对误差 全最小二乘法

0 引言

飞行体姿态测量是实现飞行体在高速旋转过程中实施精确控制的关键技术之一,它直接关系着飞行体本身的抗干扰能力和运行的稳定性。由于飞行体的控制部分空间狭小,且处于高加速度条件下,这使得陀螺、加速度计、GPS等常规测姿方案无法满足要求[1-2]。

地磁场具有的固有指向性使其可以作为天然的姿态参考坐标系,通过安装在飞行体上的GMR磁传感器可清晰地反映飞行体在运行过程中姿态的变化[3]。由于硬件系统设计缺陷,会使GMR磁传感器的零点、灵敏度和正交性等参数测量不准确,进而导致姿态角的测量误差增加。为解决这一问题,本文采用全最小二乘法对参数进行整体修正。它通过对超定方程中的系数矩阵误差和测量值误差的整体分析来提高方程解的精度。经过近几十年的发展,最小二乘法已经被广泛用于统计分析、线性和非线性回归、系统辨识和参数估计等相关领域[4-5]。

1 飞行体姿态角测量影响因素分析

飞行体姿态角通常可用滚转角γ、俯仰角θ和偏航角ψ三个欧拉角表示[6-8]。为了寻求姿态角与地磁场的对应关系,可以建立基于天、东、北、飞行体转向坐标系,发射坐标系和随动坐标系的姿态角测量模型。对模型进行推导计算,可得动态下俯仰角θ和滚转角γ的数学表达式:

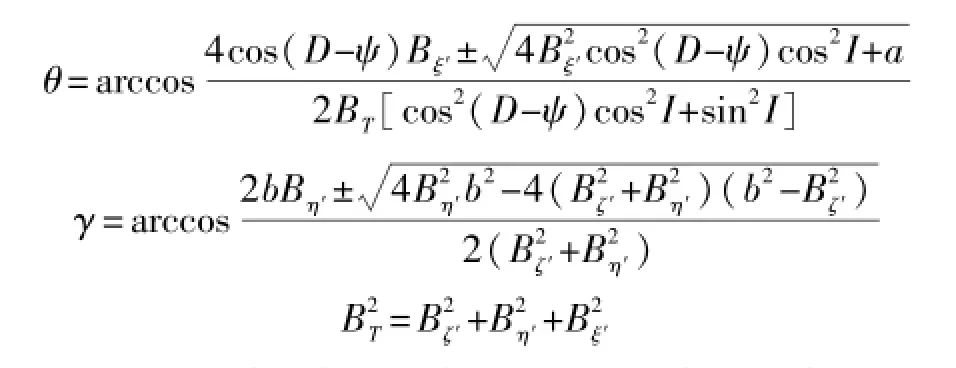
由以上公式可知,在动态条件下,俯仰角θ和滚转角γ的测量精度与磁传感器的三轴磁场分量Bζ′、Bη′、Bξ′以及地磁倾角D、地磁偏角I和偏航角ψ有关。

在整个测量模型中,分析偏航角ψ对俯仰角θ和滚转角γ测量精度的影响。假设Bξ′在理想条件下是正弦变化的,偏航角ψ的误差取值分别为0°、10°和30°,仿真结果如图1所示。

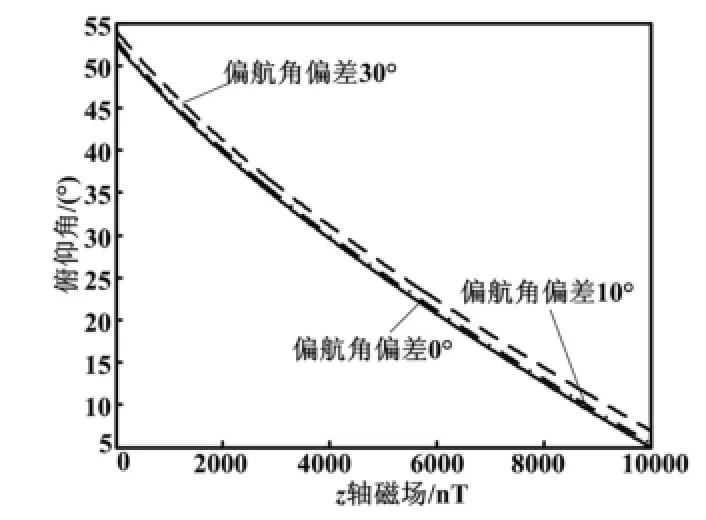
图1 偏航角对俯仰角解算的影响曲线Fig.1 Influence curves of yaw angle to the pitch angle

由图1可知,偏航角ψ的偏差在30°时对俯仰角θ的解算误差达到5.86%,在10°时的影响只有1.34%,几乎可以忽略。由于飞行体在中、短距离飞行时,飞行时间短,偏航角ψ与初始状态下相比变化通常不会超过10°,因此ψ可作为常量。姿态角的测量精度主要取决于GMR磁传感器的三轴磁场输出。

2 GMR磁传感器误差分析与建模

2.1 误差校正模型建立

GMR磁传感器输出的模拟信号经信号调理电路和A/D转换电路处理后,由微处理器输出数字信号。在硬件测量系统的设计过程中,不能确保在同一条件下三轴磁传感器输出的最终数字信号具有相同的零点误差和灵敏度。另外,硬件系统采用的是由双轴磁传感器加单轴磁传感器组成的三轴测量系统,这样还会引入正交性误差。它们的修正表达式为:

将K、A、δ代入式(1),可得:

为达到最佳逼近或拟合已知数据,最常用的一种做法是使测量值与真实值在各点间的残差在范数的条件下达到最小[7-8]。

计算模型有两种,分别为:

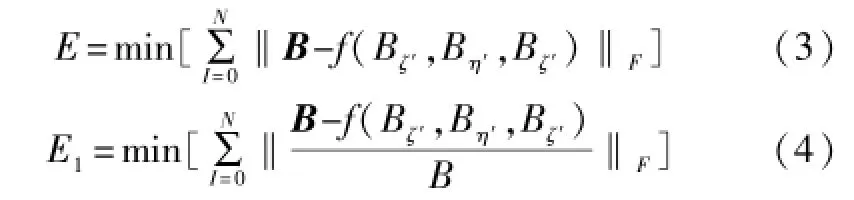
这里取F=2,求解的是向量的2范数,以式(4)的模型为例来计算补偿系数。具体方法是在经过标定的赫姆霍兹线圈中加12组不同大小的电流,分别测试GMR磁传感器每个轴的输出值Bζ″、Bη″、Bξ″和对应的总磁场Bt,得到12组磁场在x、y、z轴方向上的输出信号,将测得数据代入式(1)就可计算出补偿后的磁传感器输出值Bζ″、Bη″、Bξ″。

结合式(1)和式(4),得相对误差的通用模型为:

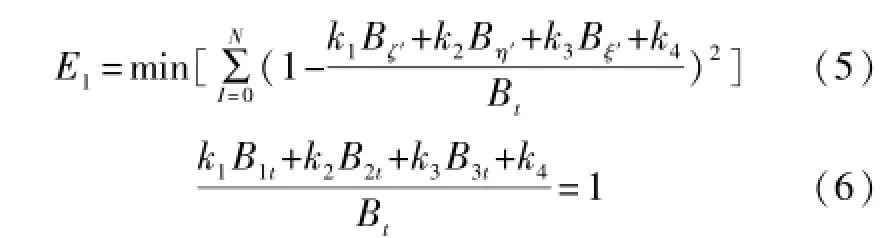
式中:k1、k2、k3、k4与式(2)中的系数存在对应关系；Bt为加不同电流下的总磁场。

将式(6)变换为矩阵形式:

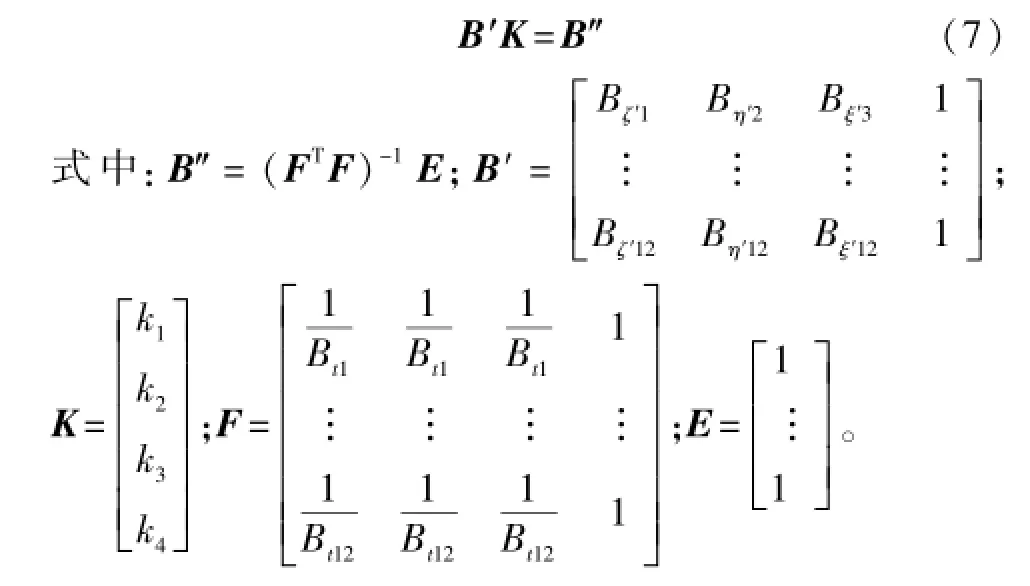
根据矩阵的逆矩阵求解方法可得补偿系数:

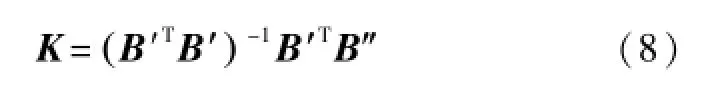
将由解算模型计算后所获得的校正值Bζ″、Bη″、Bξ″代入相应计算式,经过一定的滤波算法后由Matlab仿真,分别获得在式(3)和式(4)所示模型的总磁场BT波动曲线如图2所示。

由图2可知,常规最小二乘法所绘出的总磁场强度有较大的波动,且与真实值相比有一定的误差。这种情况的产生是由于常规最小二乘法的评价依据是针对等精度数据而言的,即观察数据在不同等级时具有大体相同的绝对误差。因此在磁传感器输出的零点信号附近很容易产生相对大的干扰,而且在点集分布不规律的情况下,拟合精度会进一步降低。

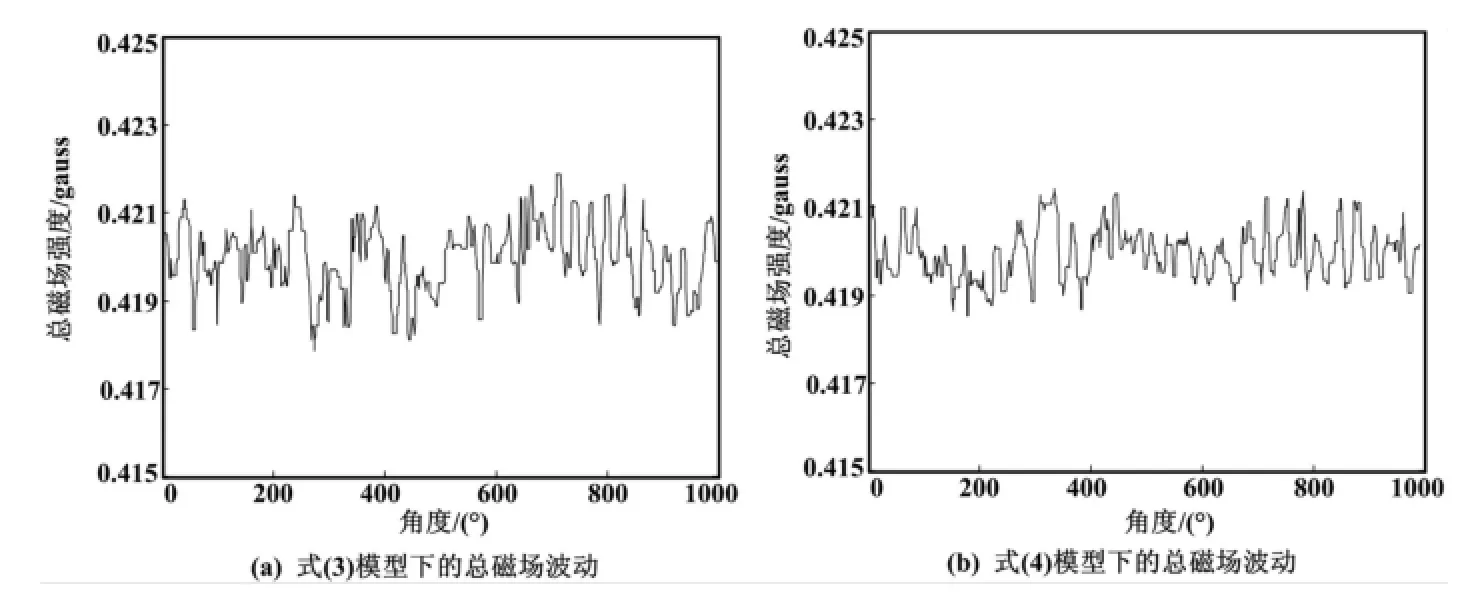
图2 不同模型下的总磁场BT波动曲线Fig.2 Fluctuation curves ofBTin different models

由于大量的科学研究和观测数据往往是按被观测量的相对误差进行评价[9],所以从相对误差的平方和最小出发,对最小二乘法进行改进,得到更符合实际情况的修正值。与常规最小二乘法相比,采用基于相对误差的最小二乘法修正后所绘出的图形具有较小的波动,在一定程度上起到了很好的校正作用,但与理想的仿真结果相比仍存在一定的误差。

除此之外,对于线性方程组Ax=b,常规最小二乘法的基本思想是在残差平方和最小的准则约束下求解最佳参数,但这里有一个前提,系数矩阵A在求解之后是作为定值代入方程中来解算未知量的。多数情况下,系数矩阵A和观测向量b会同时存在误差。常规最小二乘法只考虑了Bζ′、Bη′、Bξ′的变化,忽略了由于测量值的不准确性导致的系数矩阵K解算的不准确性。

2.2 全最小二乘求解算法

全最小二乘法的思想早在20世纪90年代就被提出了,它通过对式(7)这样的超定方程中的系数矩阵B′的误差和测量值B″的误差进行整体分析,提高方程解的精度。经过近几十年的发展,全最小二乘法已经被广泛用于统计分析、线性和非线性回归、系统辨识和参数估计等相关领域。

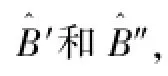
由此求出较准确的全最小二乘解K。

设具有误差的超定方程的表达式为:

式中:A∈Rm×n；b∈Rm；x∈Rn；rank(A)∈n＜m,m为观测值个数,n为待估参数个数；d和r分别为A和b的逼近误差。

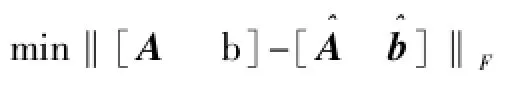
由于采用相对最小二乘法计算后得到的b是常数向量,但实质上它仍含有误差,因此并不能认为r=0。

将式(10)改写为:

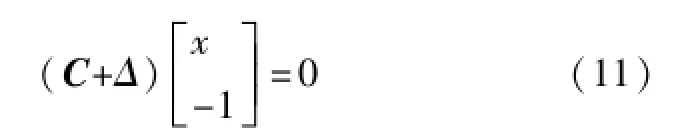
式中:C=[A,b]；Δ=[d,r]。

要求解x,则要寻找对C+Δ的最佳逼近,方程有非零解的条件是:

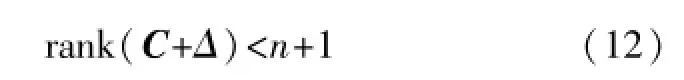
对增广矩阵C做奇异值分解:

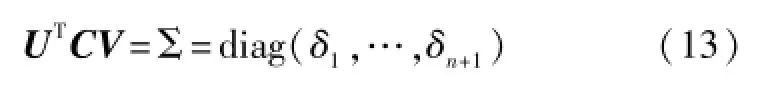
式中:V=[V1,…,Vn+1]；δ1≥δ2≥…δn+1。

若存在对C的最佳逼近C′,则C′存在这样的奇异值分解:

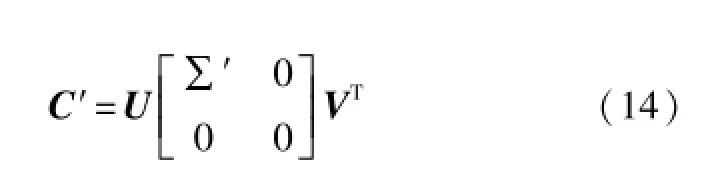
式中:∑′=diag(δ1,…,δr)。

此时方程的解可表示为:

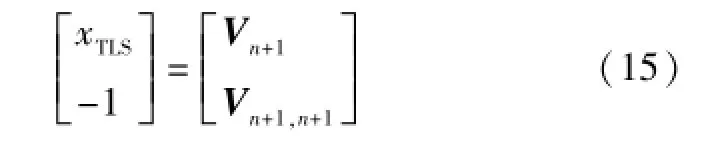
式中:Vn+1为对应于δn+1的右奇异向量；Vn+1,n+1为Vn+1的第(n+1)个值。

由于δn＞δn+1,所以Vn+1,n+1≠0。由于Vn+1为CTC对应于特征值δn+1的特征向量,故有:

将C的表达式代入式(16)得:

将式(17)改写为:

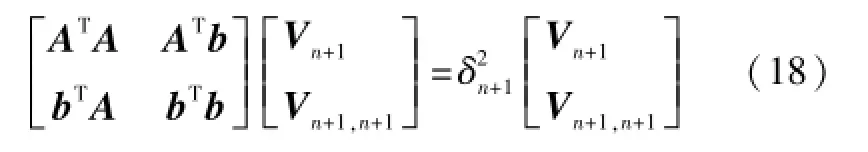
将式(18)和式(21)合并可得方程的解:

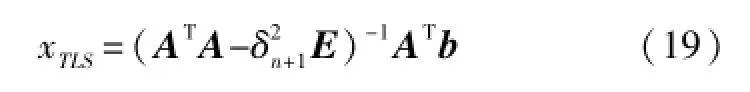
设K=xTLS、B″=b、B′=A,δn+1由C=[H,B′]的奇异值分解得到,全最小二乘法修正后的K为:

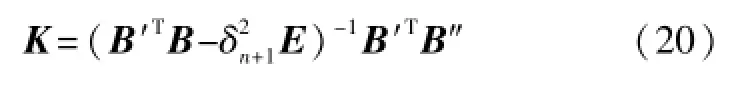
全最小二乘法和常规最小二乘法的区别在于引入了增广矩阵最小奇异值。系数矩阵和观测向量误差对增广矩阵最小奇异值的大小都有影响,但是二者对奇异值的大小的影响是不同的。当系数矩阵的扰动对增广矩阵最小奇异值大小贡献较大时,采用全最小二乘法比较合理。

由于测量参数B′本身就存在较大的测量误差,满足全最小二乘法的使用条件,因此本文采用全最小二乘法将会起到很好的参数修正作用。利用全最小二乘法修正参数后所获得的总磁场值BT经Matlab仿真,得到的校正效果如图3所示。

图3 全最小二乘法校正效果Fig.3 Correction effect of the total least squares method

3 试验验证

在相对误差的基础上采用全最小二乘法修正GMR磁传感器参数,并加入一定的滤波算法。在三维无磁转台下,规定俯仰角θ变化范围为-60°～60°,滚转角γ在0°～360°内,通过串口输出角度值,截取部分数据如表1所示。俯仰角θ和滚转角γ经过全最小二乘法修正后的误差控制在2°以内,可满足所要求的技术指标。

表1 理论值与试验值对比表Tab.1 Comparison of theoretical values and experimental values

4 结束语

本文对影响俯仰角和滚转角测量误差的因素进行分析,分别采用基于绝对误差和相对误差的最小二乘法模型对影响误差的参数进行修正。常规最小二乘法只考虑了B′的变化,忽略了B″的不准确性。而全最小二乘法模型通过对误差源进行整体处理,理论上可很好地实现校正,实际测试结果也验证了该方法的可行性,在测量范围内俯仰角θ和滚转角γ的误差基本可控制在2°以内,可很好地满足飞行体在运行过程中对姿态参数测量精度的要求。但在某些特定条件下,姿态角测量会存在较大误差,原因是磁传感器的指向进入磁场盲区范围,这是今后需要改进的地方。

[1] 郭志友,孙慧卿.磁传感器的非线性误差修正技术[J].传感器技术,2004,32(1):54-58.

[2] 郭才发,胡正东,张士峰,等.地磁导航综述[J].宇航学报, 2009,30(4):1314-1319.

[3] Jiang Dongfang,Wen Caihong.Error analysis and calibration of magnetic compass[J].Chinese Journal of Sensors and Actuators, 2010,23(4):56-61.

[4] 赵国荣,嵇绍康.磁场信号检测误差分析及补偿算法[J].系统仿真技术,2012,8(2):154-157.

[5] 牛春峰,刘世平,王中原.高速旋转弹位置与姿态测量数据分析方法[J].火力与指挥控制,2012,37(5):90-92.

[6] 邓江涛.基于地磁原理的弹体滚转姿态探测装置研究[D].南京:南京理工大学,2010.

[7] 王长青,张一农,许万里.运用最小二乘法确定后评估指标权重的方法[J].吉林大学学报,2008,34(3):513-517.

[8] 李思成.基于相对误差意义下的最小二乘法[J].数理统计与管理,2003,22(4):36-40.

[9] 王毅敏,马丽英.传统最小二乘法曲线拟合的缺陷及其改进[J].电力学报,1997,12(1):51-54.

Application Study of the Total Least Squares Method in Measurement of Attitude Parameters

In accordance with the measuring system established by 3-axes GMR magnetic sensor for attitude of flight body,the mathematical relationship between geomagnetic field and attitude angle is derived,and the factors affecting the measurement accuracy are analysed.Through comparing the corrected results for parameters of magnetic sensor by using absolute least squares method and relative least squares method,it is found that because the conventional least squares method only considers the single factor,larger fluctuation and error exist in the threecomponent of magnetic filed and the total magnetic field value.In order to solve this problem,overall correction is conducted to the parameters of magnetic sensor by adopting the total least squares method.The experiments on non-magnetic turntable prove that this method improves the measurement accuracy of magnetic field and attitude angle.

GMR magnetic sensor Rolling angle Pitching angle Attitude measurement Relative error Total least squares method

TP216+.1

A

修改稿收到日期:2013-11-03。

曹平军(1987-),男,现为中船重工第710研究所检测技术与自动化装置专业在读硕士研究生;主要从事磁场探测与信息技术的研究。