用于复合材料缺陷可视化检测的l1正则化算法

薛倩 马敏 王化祥 詹湘琳

(中国民航大学航空自动化学院1,天津 300300;天津大学电气工程与自动化学院2,天津 300072)

用于复合材料缺陷可视化检测的l1正则化算法

薛倩1马敏1王化祥2詹湘琳1

(中国民航大学航空自动化学院1,天津 300300;天津大学电气工程与自动化学院2,天津 300072)

随着复合材料在民用飞机中越来越广泛的应用,复合材料缺陷的在线检测对无损检测技术提出了更高要求。为提高平面电容层析成像(ECT)系统的成像质量,从而提高其对复合材料缺陷的检测精度,对基于l1正则化的成像算法进行了研究。采用交替最小化方法进行数值计算,并结合迭代阈值法,对重建图像进行降噪。试验结果表明,与ECT中常用的Landweber、Tikhonov正则化等算法相比,该方法能够有效分辨物场中的不同介质,提高了成像质量和被测物体边缘分辨率。

层析成像 无损检测 图像重建 复合材料 正则化

0 引言

先进复合材料(acomposite materials,ACM)因其质量轻,隔热、隔音、减震效果好,比强度高、抗腐蚀、耐高(低)温等特点,在现代民用飞机中获得了广泛应用[1]。新研制的波音系列飞机的机翼、机身等主承力机构均由ACM制成,空客A380也大量采用了ACM[2]。由于ACM具有各向异性等特点,其损伤机理、失效形式都与金属材料显著不同,这给无损检测技术带来了新的挑战。当非金属复合材料发生疲劳或损伤时,其介电常数也发生相应变化。因此,理论上可利用基于电容敏感机理的电容层析成像(electrical capacitance tomography,ECT)技术实现在线监测[3-4]。平面ECT技术用于材料无损检测的研究起步较晚,基本还处于仿真试验阶段[5-7],主要的困难在于该技术空间分辨率较低。因此,本文通过图像重建算法的研究,提高系统的空间分辨率。

1 系统结构与数学模型

平面ECT系统主要由三部分组成:平面阵列电容传感器、电容测量与数据采集电路和成像计算机。平面ECT系统结构框图如图1所示。

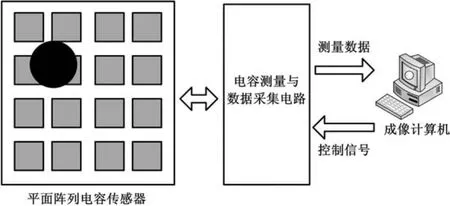
图1 平面ECT系统结构框图Fig.1 Structure of the planar ECT system

ECT系统通过传感器的阵列电极获得敏感场内介质分布状况的边界信息。电容测量及数据采集电路对传感器的输出电容值进行滤波、变换、放大,并将数据传给成像计算机。成像计算机利用图像重建算法重构被测介质的分布情况,同时向数据采集系统发送控制信号。

根据似稳场理论的Maxwell方程,对于均匀、线性、各向同性的介质,ECT敏感场内任意一点满足拉普拉斯方程,即:

由电场的唯一性定理可知,满足拉普拉斯方程和给定边界条件的φ(x,y)是给定静电场的唯一解。本文中ECT系统采用电压激励,激励电极的电势为U,其余电极电势为0,符合Direchlet边界条件,即:

式中:∂Ω为场域边界。

电势分布φ(x,y)与介电常数分布e(x,y)通过积分方程相联系。基于扰动理论和有限元法,得到线性化和离散化的图像重建模型为:

将式(3)归一化处理后,表示为:

式中:C为M×1维的测量数据向量,M代表独立测量数;g为N×1维的介电常数分布图像向量,N代表被测场域的剖分单元数;S为M×N维的灵敏度矩阵。

2 图像重建算法研究

2.1 数学模型变换

在实际ECT系统中,可测量的边界值数目往往远小于剖分单元数,即线性方程组(4)是欠定的,因此解不存在或不唯一。通常将式(4)的求解转化为求最小二范数解的凸优化问题[8-9],即:

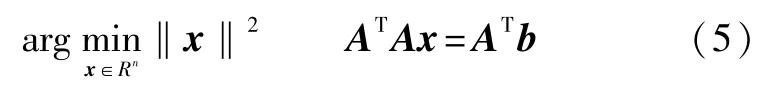
式中:A为式(4)中的灵敏度矩阵S;b为测量数据向量C;x为要求解的图像向量g。

求解此问题常用的算法有共轭梯度法和Landweber迭代法等。由于测量值C中不可避免地包含噪声,而灵敏度矩阵S的条件数通常很大,为了较准确和稳定地重建g,一般采用Tikhonov正则化方法将图像重建问题转化为:

由于泛函数Ja(x)是光滑的,可直接令其导数为零,求得Ja(x)的极小点x=(ATA+αI)-1ATb作为Ax= b的正则化近似解。由此可证明ATA+αI的逆总是存在的,故解存在。当A是线性算子时,Ja(x)是严格凸的,故存在唯一的极小点。

基于L2范数的Tikhonov正则化方法,容易使解过度光滑化。复合材料缺陷检测中被测区域的介质往往存在不连续性,采用该方法不可避免地会降低空间分辨率;且如果A是非线性的,Ja(x)不再是严格凸的,可能有多个局部极小点。不同的迭代初值可能导致不同的极值点,可能最后得到不合理的解。为削弱图像的平滑性,可考虑基于稀疏性的l1正则化。1992年, Rudin等人提出总变差(total variation,TV)正则化算法[10]并将其应用于图像去噪。后来,该算法分别由Fang(2004)、Soleimani(2005)和Wang(2007)等人引入ECT图像重建[11-13]。基于TV正则化的图像重建算法以成像区域内像素值的总变差作为惩罚项,由于同样的TV值允许函数有不同的表达形式,包括不连续的函数形式,这就使得介质分布不连续的区域得到较好的重建。该算法在提高逆问题求解稳定性的同时,对介质分布不连续区域的分辨力也明显提高,具有良好的保边缘性。ECT中图像总变差的离散化形式为:

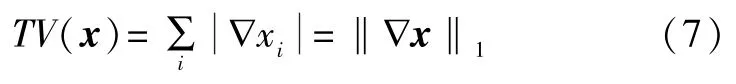
可见,TV正则化相当于利用梯度算子将图像稀疏化,然后求最小l1范数解。实际上,TV正则化可通过引入分离变量转化为l1正则化形式[14]。由于增加了l1范数的惩罚项,优化问题不再是光滑的,求解难度增加。一种鲁棒的算法是原始-对偶内点法。由于该算法效率很低,Wang等利用总变差表达式的一种二次可微的近似形式,采用牛顿-拉夫逊迭代算法求解[13]。

除TV正则化外,由于大部分图像都可经离散余弦变换(discrete cosine transform,DCT)、离散傅里叶变换(discrete Fourier transform,DFT)或小波变换等获得稀疏表达形式,在图像重建中也可将稀疏化的图像向量的l1范数作为惩罚项,以提高空间分辨率,因此,图像重建问题转化为基于l1范数的凸优化问题,即:

式中:μ＞0为权重参数。

基于凸优化理论,稀疏向量x∈iN可由少量线性测量值b=Ax∈iM重建。由此,压缩传感领域求解l1问题的各种算法都可用于测量数据有限的CT/ECT图像重建,唯一的问题在于算法效率。2011年,Yang J F等将优化领域的经典算法——交替方向法(alternating direction method,ADM)扩展到8种不同形式的l1范数最小化问题[15]。基于增广Lagrangian函数和交替最小化思想的交替方向算法,在测量数据受噪声污染的情况下能获得较准确的解。与现存的许多一阶算法相比,该算法效率较高且通用性强。

2.2 数值求解算法

对式(8)中的变量进行下列代换:

通过Legendre变换求得f和g的共轭函数:

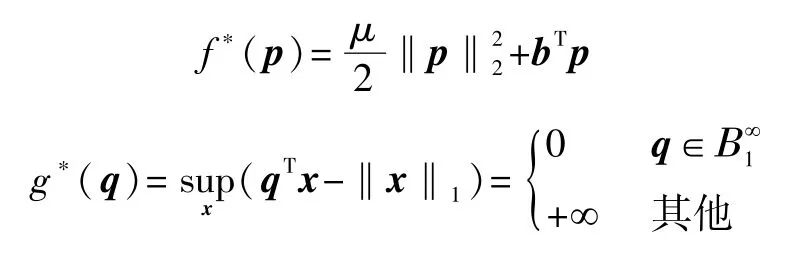
则式(8)的对偶问题可表示为:

令λ=-p,则式(10)等价于:

引入向量z∈iN,消除δz(q)项,将式(11)转化为带约束的最大化问题,即:

利用增广Lagrangian函数,将式(12)转化为无约束最小化问题,即:

式中:x∈iN为Lagrangian乘子(即原问题中的图像向量x);β＞0为惩罚系数。

相对普通的Lagrangian函数,增广Lagrangian函数多一个关于约束的惩罚项。采用交替方向(ADM)算法,在每次迭代中交替更新原始变量x和对偶变量λ、z,先给x和z(或λ)赋初值,通过最小化增广拉格朗日函数,得到新的λ(或z),并更新z(或l),由新的l和z更新乘子x,依此迭代,最终x将收敛到原问题的最优解。本文采用线性反投影(linear back projection,LBP)法重建结果作为x的初值。

式(13)关于λ的最小化问题是一个最小二乘问题。通过对λ求导,得:

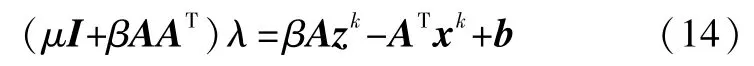
给定xk和zk,采用最速下降法求解式(14),迭代步骤如下。

由λ=λk+1和给定的x=xk,利用式(13)对z的导数更新向量z:

最后,利用λ=λk+1和z=zk+1更新x:

φ(x)与φd(λ)间的对偶间隙为:

由此,迭代终止条件设为:对偶间隙小于某一正数或解已经稳定,即Δ＜ε或‖xk+1-xk‖2/‖xk+1‖2＜θε,其中参数ε＞0,θ∈(0,1]。

2.3 迭代方法选取阈值

为提高重建图像的空间分辨率,利用迭代方法自适应设定阈值,将像素值小于阈值的像素置零,以消除重建图像中的伪影。

①迭代次数k=0,设置初始阈值T0为图像全部像素的平均值。

②将重建图像像素分为两部分:Xa和Xb。其中, Xa代表值大于Tk的像素,Xb代表其他像素。

③分别计算Xa和Xb中像素的平均值:Ta=mean(Xa)、Tb=mean(Xb)。

3 试验验证

3.1 试验条件

试验用平面ECT系统如图2所示。系统采用4× 4的矩形电极传感器,电极尺寸为2 cm×2 cm,电极间距为0.5 cm。检测对象为长、宽、高均为2 cm的正方体有机玻璃,介电常数约为3,分别放置在传感器的不同位置,以测试ECT敏感场不同位置处的检测精度。

3.2 试验结果

分别用Landweber算法、Tikhonov正则化算法和l1正则化算法进行图像重建,结果如图2、图3和图4所示。

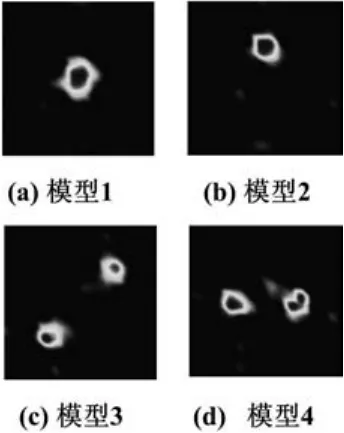
图2 Landweber算法对不同模型的重建图像Fig.2 The reconstructed images using Landweber algorithm for different models

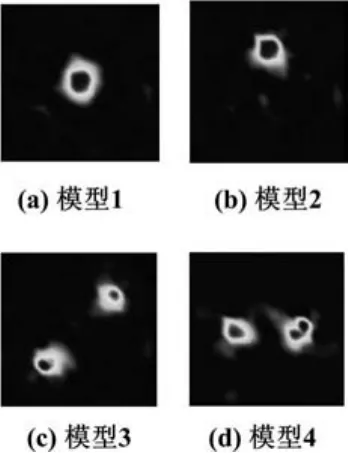
图3 Tikhonov正则化算法对不同模型的重建图像Fig.3 The reconstructed images using Tikhonov regularization algorithm for different models

图4 l1正则化算法对不同模型的重建图像Fig.4 The reconstructed images using l1regularization algorithm for different models

由图2可知,Landweber算法对敏感场中心和偏上侧位置的物体均可较好地重建,但物体形状有失真,边缘处模糊情况较严重,重建物体的尺寸随着物体放置位置的不同也发生变化;对两个物体的重建图像,可分辨出两个物体,但形状和尺寸的失真更为严重。由图3可知,Tikhonov正则化算法对重建图像质量的改善不明显,可探测出物体的存在和大致位置,但重建的形状和尺寸存在比较严重的失真。由图4可见,l1正则化算法有效改进了成像质量,提高了物体边缘的空间分辨率,从而改善了平面ECT系统的检测性能。

4 结束语

本文以平面ECT技术在航空复合材料缺陷检测中的应用为背景,利用l1正则化方法改进ECT图像重建算法。16电极平面ECT样机试验结果表明,该方法明显提高了重建图像质量,特别是敏感场内物质界面处的空间分辨率,提高了平面ECT系统的检测精度,为平面ECT系统用于航空复合材料检测提供了一定的试验论证。

[1] 杨乃宾.新一代大型客机复合材料结构[J].航空学报,2008,29(3): 596-603.

[2] 周正干,肖鹏,刘航航.航空复合材料先进超声无损检测技术[J].航空制造技术,2013(4):40-43.

[3] Xue Qian,Wang Huaxiang,Yang Chengyi,et al.Dynamical lag correlation exponent based method for gas-solid flow velocity measurement using twin-plane electrical capacitance tomography[J].Measurement Science and Technology,2012,23(8):085301-085307.

[4] 王挺.基于电容敏感机理的飞机复合材料检测方法研究[D].天津:中国民航大学,2013.

[5] Thiele S,Silva M J D,Uwe H.Capacitance planar array sensor for fast multiphase flow imaging[J].IEEE Sensors Journal,2009,9(5): 533-540.

[6] Chen D X,Hu X H,Yang W Q.Design of a security screening system with a capacitance sensor matrix operating in single-electrode mode[J].Measurement Science and Technology,2011,22(11): 114026-114032.

[7] Sun J T,Yang W Q.Fringe effect of electrical capacitance and resistance tomography sensors[J].Measurement Science and Technology,2013,24(7):074002.

[8] 张玲玲,王化祥,范文茹.基于1范数的电阻层析成像图像重建算法[J].天津大学学报,2011,44(9):786-790.

[9] Zhang Lingling,Xu Genqi,Xue Qian,et al.An iterative thresholding algorithm for the inverse problem of electrical resistance tomography[J]. Flow Measurement and Instrumentation,2013,33:244-250.

[10] Rudin L I,Osher S,Fatemi E.Nonlinear total variation based noise removal algorithms[J].Physica D,1992,60(1-4):259-268.

[11] Fang W F.A nonlinear image reconstruction algorithm for electrical capacitance tomography[J].Measurement Science and Technology, 2004,15(10):2124-2132.

[12] Soleimani M,Lionheart W R B.Nonlinear image reconstruction for electrical capacitance tomography using experimental data[J]. Measurement Science and Technology,2005,16(10):1987-1996.

[13] Wang H X,Tang L,Cao Z.An image reconstruction algorithm based on total variation with adaptive mesh refinement for ECT[J].Flow Measurement and Instrumentation,2007,18(5-6):262-267.

[14] Wang Y,Yang J,Yin W,et al.A new alternating minimization algorithm for total variation image reconstruction[J].SIAM Journal on Image Sciense,2008(1):948-951.

[15] Yang J F,Zhang Y.Alternating direction algorithms for l1-problems in compressive sensing[J].SIAM Journal on Scientific Computing, 2011,33(1):250-278.

l1Regularization Algorithm Used in Visualization Defect Inspection for Composite Materials

Along with the composite materials have been used more widely in civil aircrafts,the online inspection of the defects of composite materials requests higher level non-destructive inspecting technology.In order to improve the imaging quality of planar electrical capacitance tomography(ECT)system for enhancing the inspection accuracy for defects of composite materials,the imaging algorithm based on l1-regularization is researched,by applying alternating minimization method for numerical calculation,and combining with the iterative threshold method,the noise reduction is conducted for the reconstructed images.The experimental results show that comparing with the commonly used Landweber or Tikhonov regularization algorithms,this method can effectively distinguish different media in object field,and improve the imaging quality and the resolution for the edge of the measured object.

Tomography Non-destructive testing Image reconstruction Composite materials Regularization

TP207

A

国家自然科学基金青年科学基金资助项目(编号:61102096);

天津市科技支撑计划基金资助项目(编号:11ZCGHHZ00700);

中央高校基本科研业务费中国民航大学专项基金资助项目(编号: 3122013C007);

中国民航大学科研启动基金资助项目(编号:2013QD01S)。

修改稿收到日期:2014-04-02。

薛倩(1987-),女,2013年毕业于天津大学控制科学与工程专业,获博士学位,讲师;主要从事无损检测技术的研究。