改进型T-S模糊神经网络风电功率预测模型的研究

张维杰田建艳,2王芳,2张晓明韩肖清王 鹏

(太原理工大学信息工程学院1,山西 太原 030024;新型传感器与智能控制教育部与山西省重点实验室2,山西 太原 030024;太原理工大学电气与动力工程学院3,山西 太原 030024)

改进型T-S模糊神经网络风电功率预测模型的研究

张维杰1田建艳1,2王芳1,2张晓明1韩肖清3王 鹏3

(太原理工大学信息工程学院1,山西 太原 030024;新型传感器与智能控制教育部与山西省重点实验室2,山西 太原 030024;太原理工大学电气与动力工程学院3,山西 太原 030024)

为了提高风电功率的预测精度,在分析其主要影响因素的基础上,针对T-S模糊神经网络收敛速度慢、计算量大等缺点,提出了一种改进型T-S模糊神经网络风电功率预测模型。首先采用椭圆基函数作为隶属函数,扩展其接收域;其次利用模糊C-均值聚类确定其中心值;然后引入惯性项加快网络的收敛速度;最后分别对四季短期风电功率进行预测。仿真结果表明,改进型T-S模糊神经网络有效地提高了短期风电功率的预测精度,具有一定的实用价值。

风电功率预测 改进型T-S模糊神经网络 椭圆基函数 模糊C-均值聚类 惯性项

0 引言

近年来,风能的开发和利用得到高度的重视,风能作为可再生能源,具有良好的应用前景[1-3]。由于风能具有随机性和不稳定性等特点,大量风电的接入将对电力系统的稳定运行带来巨大挑战[4-5],因此,风电功率的准确预测对电网的稳定运行具有重要意义[6-8]。

目前,常用的风电功率预测方法如持续法[9]、时间序列法[10]和神经网络法等[11],没有充分考虑风速的内在规律和性质,忽略了样本信息与预测日信息之间的相似度[12]。因此,在考虑风速固有的季节性及时间连续性等特点的基础上,提出一种基于椭圆基函数(elliptical basis function,EBF)的改进型T-S模糊神经网络模型,分别对四季短期风电功率进行预测,并在Matlab平台上进行仿真。结果表明,改进型T-S模糊神经网络提高了风电功率的预测精度。

1 风电功率的主要影响因素

风力机是将风叶扫掠面内的一部分动能转换成有用的机械能,带动发电机发电的一种装置,其输出的功率为[13]:

式中:P为实际获得的输出功率;Cp(λ,γ)为风能利用系数;λ为叶尖速比;γ为桨距角;ρ为空气密度;S为风轮的扫面面积;υ为风速。

由上式可知,输出功率P与风能利用系数Cp(λ,γ)、空气的密度ρ、风轮的扫面面积S及风速υ的三次方成正比。对于风力机,其转子叶片的扫风面积S是固定的,因此,影响输出功率P的主要因素有风能利用系数Cp(λ,γ)、风速υ、风向、空气密度ρ。但在实际中风能利用系数很难测量得到,空气密度随地理位置、海拔、地形等因素而变,只能近似通过测量气压和环境温度进行计算。空气密度近似的计算公式为:

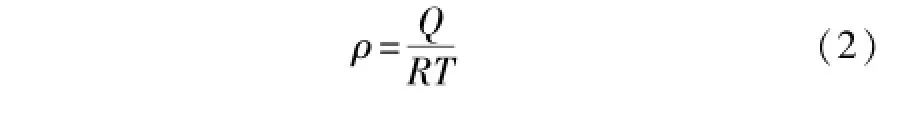
式中:Q为气压;R为气体常数;T为环境温度。

而空气密度ρ主要与环境温度T有关,故选择环境温度T来代替空气密度作为影响风电功率的主要因素之一。

因此,影响风电功率的主要因素有风速、风向和环境温度。由于不同年份的同一季节以及同一季节的不同月份的风速具有一定的周期性,考虑到风速随季节周期性变化,分别将四个季节的风速、风向和环境温度作为改进型T-S模糊神经网络的输入对风电功率进行分季预测,进一步提高预测精度。

2 改进型T-S模糊神经网络

模糊神经网络(fuzzy neural network,FNN)在控制领域里已经成为一个研究热点,其原因主要在于模糊神经网络兼有模糊系统和神经网络的性质。T-S模糊神经网络是模糊神经网络最常用的一种,它由前件网络和后件网络组成,其网络结构如图1所示。

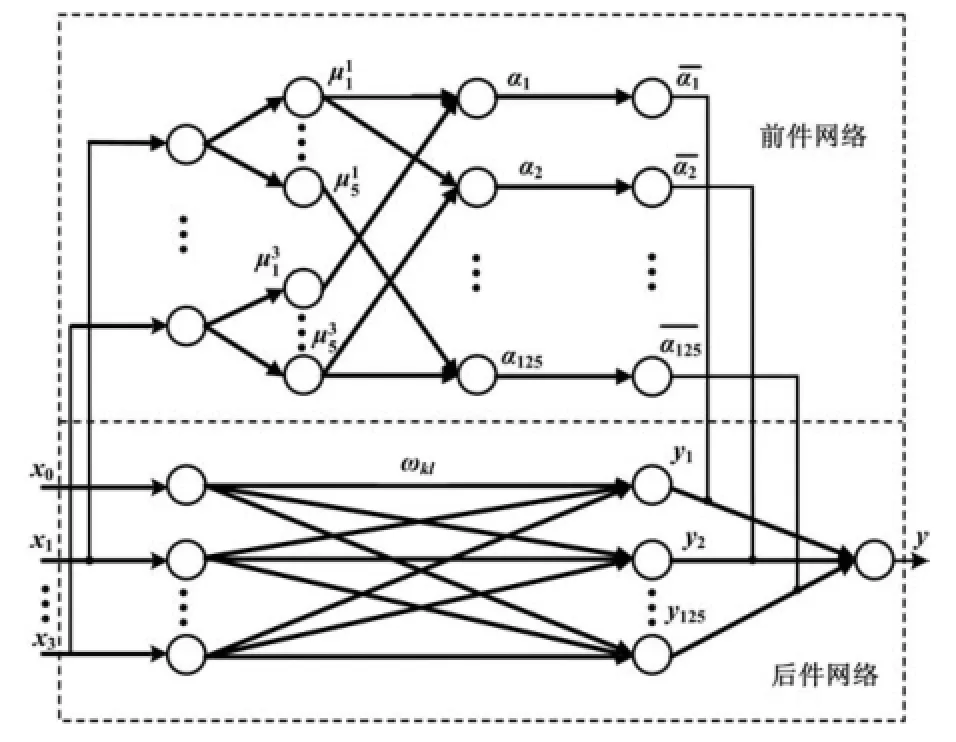
图1 改进型T-S模型的网络结构图Fig.1 Network structure of the improved T-S model

2.1 前件网络

前件网络由4层组成,分别为输入层、模糊化层、模糊推理层、归一化层。

2.1.1 输入层

第一层为输入层,它的每个节点直接与输入向量的各分量连接,并将其传递到下一层。通过对影响风电功率的主要因素进行分析研究,本文将风速、风向和环境温度作为改进型T-S模糊神经网络的输入,因此该层的节点个数N1=3。

2.1.2 模糊化层

第二层为模糊化层,它是计算各输入分量属于其语言变量值的模糊隶属度。若输入分量的言变量值个数太少,会降低模型的泛化能力;反之,会使网络更加复杂,计算量增加。因此,本文经大量仿真,确定每个输入的模糊分割数为5,则该层节点个数N2=3×5=15。

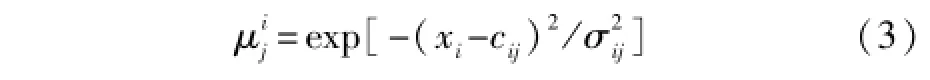
式中:为xi的第j个语言变量的隶属度,其中i=1,2, 3,j=1,2,…,5;cij和σij分别为高斯函数的中心和宽度。

2.1.3 推理层

第三层为推理层,每个节点代表一条模糊规则推理结果,它用来匹配模糊规则的前件,并计算每条规则的适应度,采用乘积法,即:

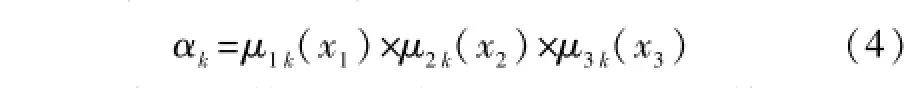
由于高斯函数具有良好的平滑性,因此传统的T-S模糊神经网络通常采用高斯函数作为隶属度函数,但存在每个输入变量的所有高斯函数的宽度均相等的缺点。本文采用椭圆基函数代替高斯函数作为隶属度函数,以扩展其接收域,并计算其适应度。适应度为:

式中:σ1k、σ2k、σ3k分别为每个输入对应的宽度。

为了避免椭圆基函数初始中心值选择的随机性,减少训练时间,本文采用模糊C-均值聚类对其进行确定。该算法是一种基于函数最优方法的聚类算法,它具有设计简单、解决问题范围广、易于计算机实现等特点。采用模糊C-均值聚类选取椭圆基函数中心的具体步骤如下[15]。

①初始化椭圆基函数的隶属矩阵U,使其矩阵中元素的初值为[0,1]的随机数且有:

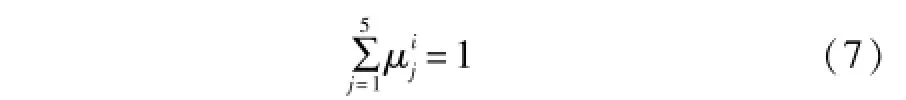
式中:为xi的第j个语言变量对应的隶属度,∈U且U为3×5的矩阵。

②根据式(8)计算C聚类中心cj:

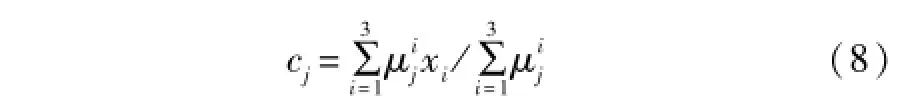
③根据式(9)计算价值函数J。若它小于某个确定的阈值ε,则算法停止;反之,则更新隶属矩阵U,直到满足条件为止。

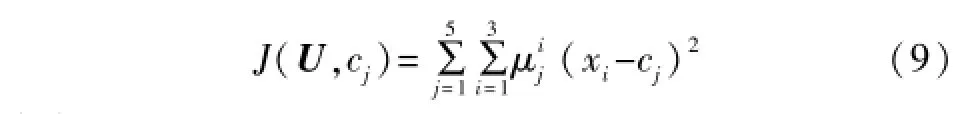
式中:k=1,2,...,m;m=53=125。

该层节点数N3=125。其中,的更新公式为:

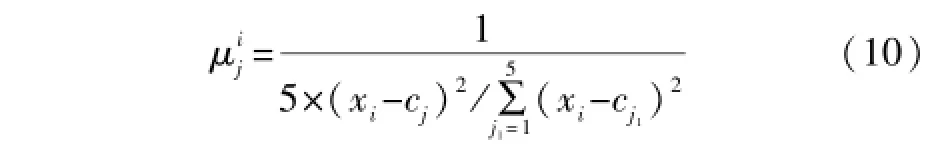
2.1.4 归一化层

第四层为归一化层,它所实现的是归一化计算,即:

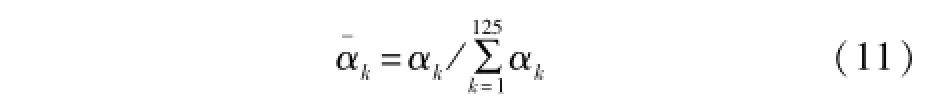
该层的节点数N4=N3=125。

2.2 后件网络

后件网络是由多个结构相同的并列子网络所组成,每个子网络产生一个输出量。由于本文只有一个输出量即风电功率,因此后件网络只由1个子网络组成。它的第一层是输入层,负责将输入变量传递到下一层,其中第0个节点x0=1为模糊规则后件提供常数项。

子网络第二层的每个节点代表一条规则推理结果,它是计算每条规则的后件,即:

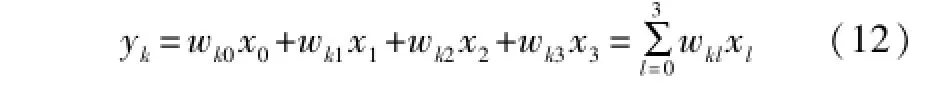
式中:k=1,2,…,125;l=0,1,2,3;wkl为后件网络中第l个输入对应第k个输出的权重。

子网络第三层为系统的输出,即:

2.3 网络学习算法

传统的T-S模糊神经网络采用梯度下降法,其学习过程容易发生振荡且收敛速度比较慢,故进一步引入惯性项,利用一阶梯度加惯性项算法来调节cij、σij和wkl。

定义的误差函数为:

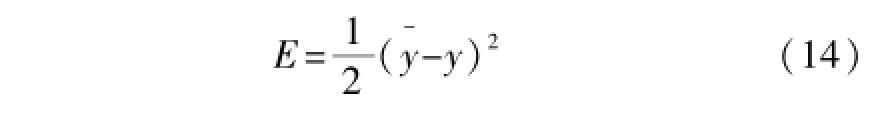
最后参数调整的学习算法为:

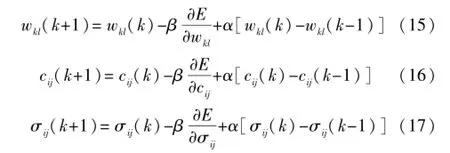
式中:β为学习速率,通常β∈(0,1);α为惯性系数,通常α∈(0,1)。

3 不同季节的风电功率预测

为了进一步提高风电功率的预测精度,充分利用风速随季节性变化的规律,本文分别对一年四季的风电功率输出进行预测。由于篇幅有限,本文仅给出某风电场春季风电功率预测图。将春季的风速、风向和环境温度作为改进型T-S模糊神经网络模型的输入,每个输入的模糊分割数为5,采样周期为1 h,采用前1 100组数据进行学习训练,并对后100组数据进行预测。

对于学习速率β,如果β太小,收敛性虽能得到保证,但学习速度太慢,耗时太长;如果β太大,学习速度快,但可能导致振荡和发散。对于惯性系统α,如果α太小,学习速率太慢;如果α太大,易发生振荡,预测相对不准确。因此,通过大量仿真,确定学习速率β为0.01,惯性系数α为0.6。分别采用T-S模糊神经网络和改进T-S模糊神经网络对风电功率进行预测,预测结果及误差曲线如图2和图3所示。

图2 T-S和改进型T-S模型春季风电功率预测图Fig.2 The wind power prediction in spring using T-Sand improved T-S model

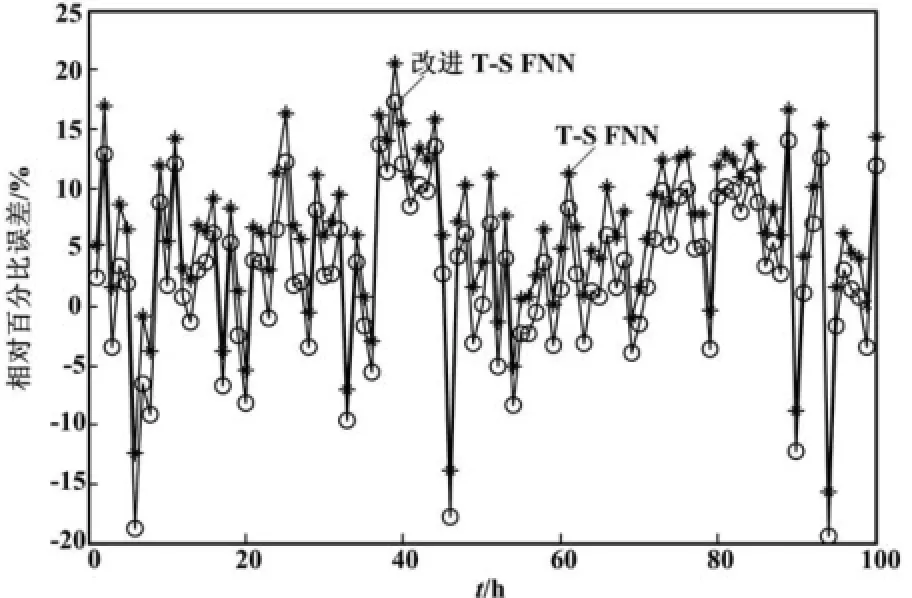
图3 T-S模型和改进型T-S模型春季误差图Fig.3 The error of spring prediction using T-S and improved T-S model

由图可知,改进型T-S模糊神经网络模型不仅提高了风电功率的预测精度,而且绝对百分比误差相对较小。为了定量地评价改进型T-S模糊神经网络模型的有效性,本文分别计算两种模型四季的平均绝对误差(MAE)、平均绝对百分误差(MAPE)[16]和最大绝对值误差Emax,其计算公式分别为:

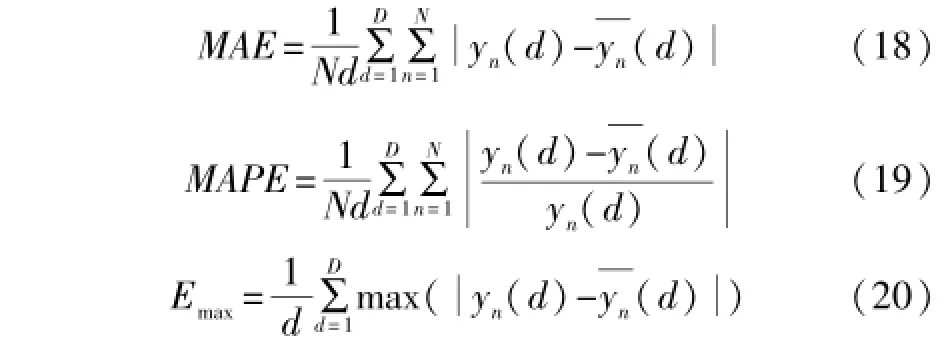
T-S模型和改进型T-S模型四季的上述评价指标计算结果如表1所示。

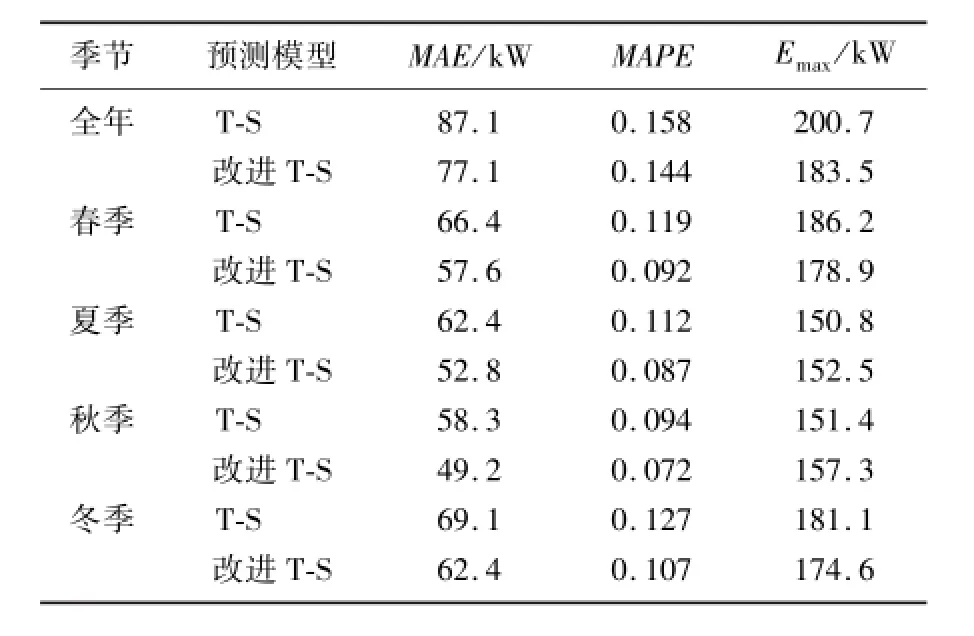
表1 T-S模型和改进型T-S模型预测误差Tab.1 The prediction errors using T-S model and improved T-S model

由表1可知,不同季节风电功率预测精度有所差别,但总体上改进型T-S模糊神经网络较T-S模糊神经网络的平均绝对误差(MAE)、平均绝对百分误差(MAPE)和最大绝对值误差Emax有所提高,而且有效地减少了较大误差的出现频率,使预测误差曲线更加平稳。

4 结束语

由于风能的随机性、间歇性等特点,导致风电场的输出功率具有随机性。本文首先采用椭圆基函数代替高斯函数,使其接收域更加广泛灵活,并利用模糊C-均值聚类确定椭圆基函数的中心值,减少训练时间;其次引入惯性项,加快了T-S模糊神经网络收敛速度;最后对四季风电功率进行了预测。通过与T-S模糊神经网络的各评价指标进行对比分析,仿真结果表明,基于改进型T-S模糊神经网络模型不仅预测精度得到了整体的提高,而且较大误差出现的频率得到了有效的减少,说明此方法具有一定的实用价值。

[1] Mabel M C,Fernandez E.Analysis of wind power generation and prediction using ANN:a case study[J].Renewable Energy,2008(33): 986-992.

[2] 王丽婕,廖晓钟,高阳,等.风电场发电功率的建模和预测研究综述[J].电力系统保护与控制,2009,37(13):118-121.

[3] Haouas N,Bertrand P R.Wind farm power forecasting[J]. Mathematical Problems in Engineering,2013:1-5.

[4] 吕跃刚,关晓慧,刘俊承.风力发电机组状态监测系统研究[J].自动化与仪表,2012(10):6-10.

[5] 王鹏,陈国初,徐余法,等.改进的EMD及其在风电功率预测中的应用[J].控制工程,2011,18(4):588-591.

[6] 张宁宇,高山,赵欣.一种考虑风电随机性的机组组合模型及其算法[J].电工技术学报,2013,28(5):22-28.

[7] 武小梅,白银明,文福拴.基于RBF神经元网络的风电功率短期预测[J].电力系统保护与控制,2011,39(15):80-83.

[8] 夏冬,吴俊勇,贺电,等.一种新型的风电功率预测综合模型[J].电工技术学报,2011,26(1):262-266.

[9] 方江晓,周晖,黄梅.基于统计聚类分析的短期风电功率预测[J].电力系统保护与控制,2011,39(11):67-78.

[10] De Giorgi M,Ficarella A,Tarantino M.Error analysis of short term wind power prediction models[J].Applied Energy,2012(88): 1298-1311.

[11] 叶林,刘鹏.基于经验模态分解和支持向量机的短期风电功率组合预测模型[J].中国电机工程学报,2011,31(31):102-108.

[12] 蒋小亮,蒋传文,彭明鸿,等.基于时间连续性及季节周期性的风速短期组合预测方法[J].电力系统自动化,2010,34(15):75-79.

[13] 李树江,蔡海锋,邓金鹏,等.自适应变步长最大风能捕获算法[J].控制工程,2012,19(1):68-72.

[14] 牛林,叶燎原,李明德.基于T-S模糊模型的多变量预测控制[J].自动化与仪表,2009(8):34-37.

[15] Monjoly S,Blonbou R.Configuration of a wind power forecasting model based on fuzzy c-means clustering[J].IASTED International Conference on Power and Energy Systems and Applications,PESA 2012:217-222.

[16] 刘立阳,吴军基,孟绍良.短期风电功率预测误差分布研究[J].电力系统保护与控制,2013,41(12): 65-70.

Study on the Wind Power Prediction Model Based on Improved T-S Fuzzy Neural Network

In order to improve the prediction accuracy of wind power,on the basis of analyzing the major influencing factors,and to overcome the disadvantages of T-S fuzzy neural network,e.g.,slow convergence speed and huge amount of computation,the wind power prediction model based on improved T-S fuzzy neural network is proposed.Firstly the elliptic basis function(EBF)is used as membership function to expand its receptive field;then fuzzy C-means clustering is used to determine the center value,and the convergence speed of the network is accelerated by introducing inertia term;finally the short term wind power in four seasons is predicted respectively.The simulation results show that the accuracy of wind power prediction for four seasons can be effectively enhanced by improved T-S fuzzy neural network,this method possesses certain practical value.

Wind power prediction Improved T-S fuzzy neural network Elliptic basis function Fuzzy C-means clustering Inertia term

TP183

A

国家自然科学基金资助项目(编号:51277127)。

修改稿收到日期:2014-03-04。

张维杰(1988-),男,现为太原理工大学控制理论与工程专业在读硕士研究生;主要从事复杂系统建模与智能控制方面的研究。