镜面-镜面耦合散射中心的频率依赖特性分析

邢笑宇, 闫华, 殷红成, 李胜

（电磁散射重点实验室,北京 100854）

镜面-镜面耦合散射中心的频率依赖特性分析

邢笑宇, 闫华, 殷红成, 李胜

（电磁散射重点实验室,北京 100854）

当入射波照射目标时,在某些角度范围内目标各部件之间常常存在耦合关系,导致新的强耦合散射中心产生。文章针对面-面耦合散射中心,从电磁散射机理出发,推导其后向散射电场公式,从而获得了耦合散射中心的频率依赖关系。

电磁散射；耦合散射中心；模型

0 引言

常见的散射中心模型包括非衰减指数和模型、衰减指数和（Damped Exponential,DE）模型和几何绕射理论（Geometric Theory of Diffraction,GTD）模型等[1,2]。其中,GTD模型更贴近高频电磁散射机理,且将散射中心的频率依赖因子与目标几何结构类型相联系,为散射中心提供了相对简单和比较完备的物理描述。

文献[2]、[3]给出了若干典型结构和组合体的散射中心频率依赖关系。当目标的各部件之间存在耦合结构时,目标上可能产生新的强散射源,即耦合散射中心。耦合机制广泛存在于目标的复合散射过程,在很多情况下构成了目标的强散射源。那么,是否所有基本几何形状之间的耦合散射都存在类似GTD模型的频率幂次依赖关系？目前公开发表的文献鲜有相关的描述。

因此,本文针对导体目标以镜面-镜面这类强耦合散射中心为例,研究其散射机理,分三种情形讨论耦合散射中心的频率依赖关系,推导出各情形下镜面-镜面耦合结构的频率依赖因子。本文的结论是在远场单站条件下得到的,但本文的求解方法在近场非双站条件下也适用。最后,在仿真实验中,基于GTD模型用频带分割（Spectrum Parted,SP）算法估计耦合散射中心的频率依赖因子[4],验证了理论结果的正确。

1 镜面-镜面耦合结构的分析方法

镜面-镜面的强耦合结构可分为六种类型：双弯曲-双弯曲、双弯曲-单弯曲、单弯曲-单弯曲、平面-双弯曲、平面-单弯曲、平面-平面。图1给出了各类镜面-镜面耦合情况下的典型二次反射结构。

图1 各类镜面-镜面耦合情况下的典型二次反射结构

本文将这六类耦合结构分为三种情形进行分析：

a）情形一：入射射线在与入射方向相垂直的两个独立方向上平移时,组合体对应于射线的几何结构在两个方向上都不具有平移不变性,文中称这种结构为非平移不变结构；

b）情形二：入射射线在与入射方向相垂直的两个独立方向上平移时,组合体对应于射线的几何结构仅在一个方向上具有平移不变性,文中称这种结构为单向平移不变结构；

c）情形三：入射射线在与入射方向相垂直的两个独立方向上平移时,组合体对应于射线的几何结构在两个方向上都具有平移不变性,文中称这种结构为双向平移不变结构；

在射线理论框架下,上述镜面-镜面耦合问题变成了多次反射问题。本文采用几何光学法（GO,Geometrical Optics）[5-7]、物理光学法（PO, Physical Optics）分析这类耦合问题[5]。其中, GO属于射线理论；PO用于在射线理论失效时获得对GO解的修正因子。

为了能够正确地使用射线理论,需要作如下假定：

a）入射波波长远小于各反射体表面的曲率半径；

b）入射波波长远小于反射体之间的距离；

c）忽略三次以上的镜面反射。

2 镜面-镜面耦合结构的频率依赖特性分析

2.1 非平移不变结构的频率依赖性分析

平面波入射场可表示为[6]

入射波经过A表面上的第一次反射并在B表面上进行二次反射,根据GO理论[6],二次反射点的入射场为

图2 射线基坐标系中二次反射的几何路径及极化分解

对于经第二次反射并在远场P点接收的电场有

在远场条件下,对于相位因子,如图3所示,有sr=r-。由于sr＞＞rQB,r＞＞rQB,有sr≈r-r· rQB,则相位因子

式中：rQB为目标坐标系原点O到物体B的照射表面的矢量。

扩散因子可化为

式中：r为目标坐标系原点O到接收点P的距离。

将式（1）（2）（5）（6）代入到式（4）中,得

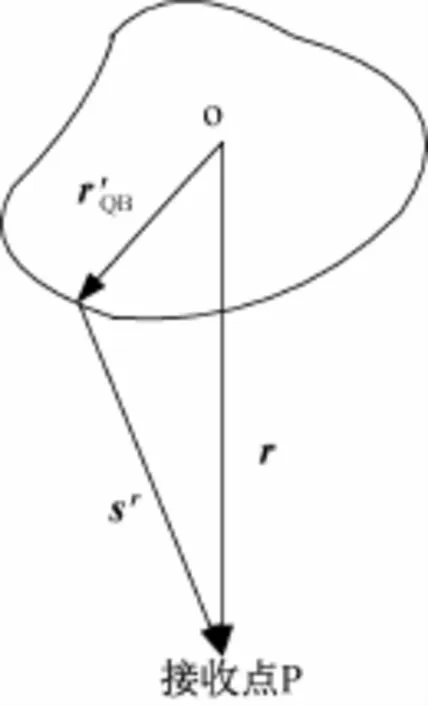
图3 接收场矢量关系

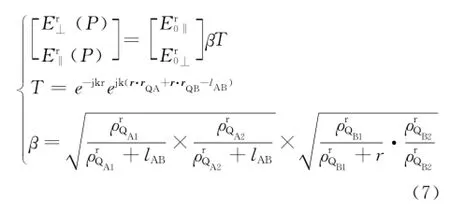
如果改变发射场的极化基方向,使其与接收场的极化基方向一致,则式（7）可简化为

即在本征极化基下的极化散射矩阵为

由此,可得到情形一的二次反射解的形式为

其中：

由式（10）可知,此时二次散射场对频率的依赖因子为0。

2.2 单向平移不变结构的频率依赖性分析

图4给出了情形二的示例。对这种情形,GO+ GO方法求解已不再适用。本文采用GO+PO方法求解,其求解方式如图5所示。当射线在第一个表面上反射时,采用GO方法来计算散射场,由于二次反射时入射方向、散射方向不再一致,为了获得第二个表面上的入射场,需要求解双站近场解。

图4 情形二的示例

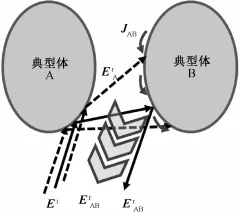
图5 GO-PO求解示意图

根据GO理论[5],第一次散射解为

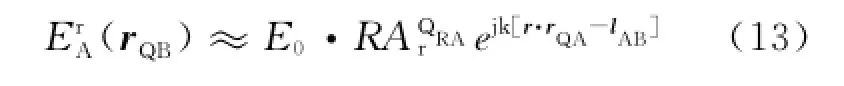
第二个表面上产生的感应电流由下两式计算[5]：

式中：lAB为从A到B的射线路径单位矢量；Z0为真空波阻抗；nB（rQB）为B表面的法向单位矢量；（rQB）（rQB）为入射到B表面的电磁场；SAB是B表面的照明区域。

最后,采用PO方法,对表面电流积分获得二次耦合散射场,计算公式为[5]

式中：l为单位矩阵；rr为两接收点P方向上的单位矢量的并乘计算。

采用驻相法求解上述积分,可获得在情形二的条件下的二次反射解[6]：

式中：Lv为射线平移不变长度。

由式（10）、式（17）对比可知,散射目标表面的几何对称性的不同导致了频率依赖性的改变。可得结论,情形二的二次散射场对频率的依赖因子为1/2。

2.3 双向平移不变结构的频率依赖性分析

图6给出了属于这种情况的组合体示意图。

图6 直二面角结构

与情形二的处理方法类似,基于GO+PO并采用驻相近似,可获得下面的公式：

不难看出,此时二次散射场对频率的依赖因子为1。

3 仿真结果

为验证上节推导的三种情形下镜面-镜面耦合散射中心GTD模型频率依赖关系,本节各选取一种组合体进行参数估计。组合体的散射回波数据由高频法计算,带宽8 GHz～12 GHz,步进频率10 MHz。图7为情形一对应的圆球-圆盘组合结构；图8为情形二对应的圆形顶帽组合结构；图9为情形三对应的二面角组合结构。

基于GTD模型,先用信号子空间旋转不变（Estimation of Signal Parameters via Rotational Invariance Techniques,ESPRIT）方法估计散射中心的位置和幅度参数[8],然后用频带分割（Spectrum Parted,SP）算法估计耦合散射中心的频率依赖因子[4]。

将估计结果与理论预测值进行对比,如表1所示。可见,所得结果与理论预测值十分接近。

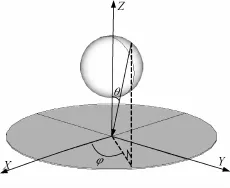
图7 圆球-圆盘组合结构

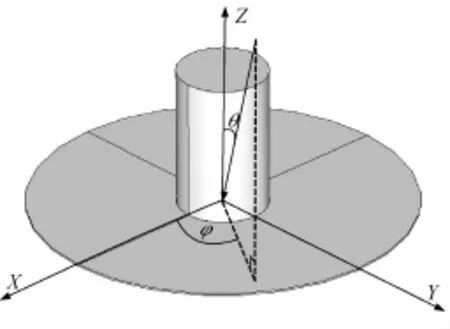
图8 圆形顶帽组合结构

图9 直二面角组合结构

表1 估计参数与理论预测值的对比分析

4 结论

针对三种情形,利用GO、PO对六类镜面反射机理的二次耦合（二次反射）效应进行分析。结果表明,二次反射场的频率依赖函数为半整数指数的幂次函数,仍然符合GTD模型。表2总结了镜面-镜面耦合结构的频率依赖关系。

表2 镜面-镜面耦合类型的频率依赖因子

有关镜面-边缘和边缘-边缘耦合类型的频率依赖关系将在后续工作中继续研究。

[1] Steadly W M,Moses R L.High Resolution Exponential Modeling of Fully Polarized Radar Returns[J].IEEE Trans.On Aerospace and Electronic Systems,1991,27（3）：459-468.

[2] Potter L C.A GTD-based Parametric Model for Radar Scattering[J].IEEE Trans.Antennas and Propagation,1995,43（10）：1058-1067.

[3] N.Akhter.Far Zone Electromagnetic Scattering from Complex Shapes using Geometrical Theory of Diffraction[J].The Ohio State University,1993.

[4] D.F.Fuller,M.A.Saville.The Spectrum Parted Linked Image Test（SPLIT）Algorithm for Estimating the Frequency Dependence of Scattering Center Amplitudes[J].Proc.of SPIE,2009（7337）：1-11.

[5] 黄培康,殷红成,许小剑.雷达目标特性[M].北京：电子工业出版社,2005：22-46.

[6] 汪茂光.几何绕射理论[M].西安：西安电子科技大学出版社,1985.

[7] J.B.Keller.Geometrical Theory of Diffraction[J].J.Opt.Soc.Am.,1962,52（1）：116-130.

[8] 王菁,周建江.一种基于GTD模型的目标散射中心提取方法[J].系统工程与电子技术,2008,30（11）：2146-2150.

Frequency-dependent Characteristics Analysis of Specular Coupling Scattering Centers

XING Xiao-yu,YAN Hua,YIN Hong-cheng,LI Sheng（Science and Technology on Electromagnetic Scattering Laboratory,Beijing 100854,China）

For the target illuminated by the incident wave,within some angle range, there is usually the coupling relationship between target components to produce a new strong coupling scattering center.Aiming at specular coupling scattering centers,the formula of backscattering electric field is derived from the physical mechanism of electromagnetic scattering,and the relationship of frequency dependence of coupling scattering centers is acquired.

electromagnetic scattering；scattering center；model

TN957.51

A

1671-0576（2014）02-0039-05

2014-02-10

973项目（2010CB731905）

邢笑宇（1987―）,女,硕士,主要从事散射逆散射方面研究。