主成分分析算法在水资源短缺因素中的应用研究

牛海军，蔡 春

（1.铁岭师范高等专科学校；辽宁 铁岭 112001；2.北京联合大学应用文理学院 北京 100191）

1 水资源风险短缺问题

北京是世界水资源严重缺乏的城市之一，人均水资源占有量不到300m3，是全国人均的1/8，世界人均的1/30，属重度缺水地区。政府虽然采取了一系列措施,但是水资源短缺的风险始终存在。如：总用水量、水资源总量、农业用水、工业用水、第三产业及生活等其它用水、污水处理、降水量、人口等都是影响水资源风险短缺的因素，因此如何对水资源风险短缺的主要因素识别，对不同风险因素采取相应的措施，对社会稳定、可持续发展战略的实施具有十分重要的意义。

本文中数据规模取自北京市1979年至2009年这30年的水资源短缺数据作为训练数据集。样本指标选择了如下因素：分别为总用水量(亿立方米)、水资源总量（亿方）、农业用水(亿立方米)、工业用水(亿立方米)、第三产业及生活等其它用水 (亿立方米)、污水处理 (亿立方米)、降水量（毫米）、人口(万)。本文利用主成分分析方法找出影响北京市水资源短缺的主要风险因素，以方便有关单位根据结果作出相对应的措施来解决有关水资源短缺问题。

2 主成分分析法来确定主要因素

通过KMO检验法决定主成分分析法可行。由于该案例中提供影响北京市总用水量的因素有7个，利用主成分分析法把多维因素进行降维。首先利用KMO检验统计量，KMO检验统计量是用于比较变量间简单相关系数和偏相关系数的指标。KMO统计量是取值在0和1之间。当所有变量间的简单相关系数平方和远远大于偏相关系数平方和时，KMO值越接近于1，意味着变量间的相关性越强，原有变量越适合作主成分分析；当所有变量间的简单相关系数平方和接近0时，KMO值越接近于0，意味着变量间的相关性越弱，原有变量越不适合作主成分分析。在SPSS软件界面中输入案例中数据，得到KMO的值为0.769，表示比较适合使用主成分分析法。其次计算矩阵的协方差

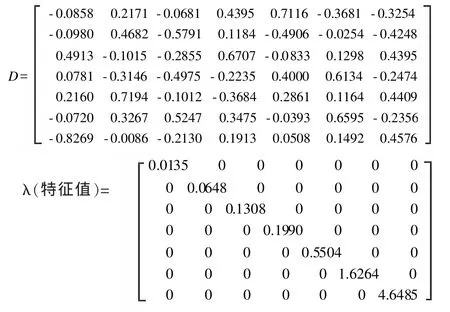
由此看出7个特征值大小不一，通过计算贡献率公式得出最后两个特征值所占贡献率为86.750%，符合主成分分析法中贡献率的要求（>80%）。因此第一个主成分为 （贡献率 64.265%），第二个主成分为 （贡献率22.485%）。

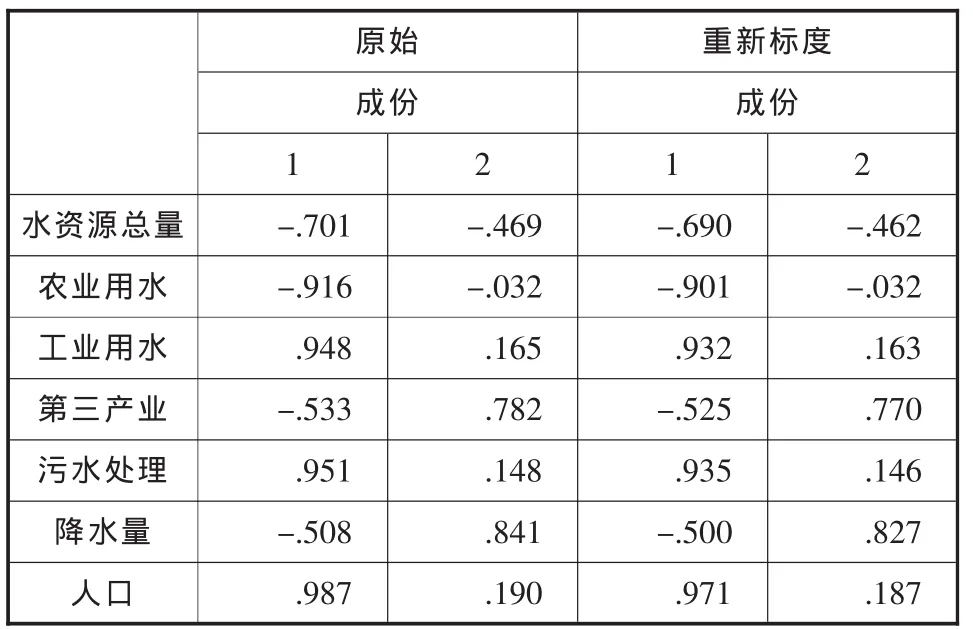
原始 重新标度成份 成份1 2 1 2水资源总量 -.701 -.469 -.690 -.462农业用水 -.916 -.032 -.901 -.032工业用水 .948 .165 .932 .163第三产业 -.533 .782 -.525 .770污水处理 .951 .148 .935 .146降水量 -.508 .841 -.500 .827人口 .987 .190 .971 .187

从上表中重新标度的成分系数来看，对应的系数越大，说明主成分对该原变量的代表性也越大。

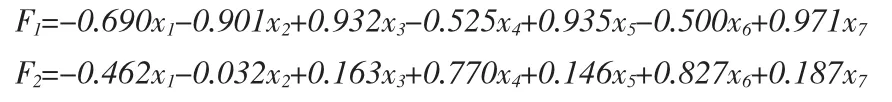
从中可以看出，相关性高的因素有：农业用水、工业用水、污水处理、人口。其中工业用水、污水处理、人口呈现正相关性，而农业用水呈现负相关性，因此包含四个指标。而中，降水量和第三产业及生活用水的正相关性最大，因此中包含降水量和第三产业及生活用水两个指标。为了更好的求解模型，我们建立对该主成分分析的载荷图：

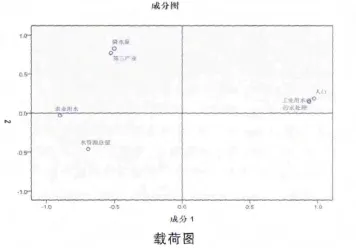
从载荷图看出，F1占64.265%的贡献率，说明其所反映的原因是最主要的。随着北京发展速度越来越快，同时增加的还有人口数量，其突出反映了北京因为人口的持续增长造成生活用水总量在总用水量中的比例持续增大。与此同时，随着经济的快速发展，工业排放出的污水导致水源地污染，水资源环境恶化。污水的随意排放反映了政府管理制度不够完善。此外，在载荷图中还可以看出，农业用水在F1中表现出负相关，资料显示农业用水有利于地表水分的积累和地下水的循环。地下和地表水量的减少都会导致水资源总量的减少。因此，F1反映出北京市水资源短缺的最重要的风险因子是人口过快增长、水污染严重、及管理制度的松懈。

同时注意到F2中相关性最大风险因子的是降水量，占贡献率的22.485%。降水量的多少关系到北京市水资源的是否丰富，能缓解其他方面对北京供水的压力。所以降水量是北京市水资源短缺的第二重要的风险因子。同时，由于居民的节水意识不强，在日常生活中用水浪费的现象十分普遍。政府应尽快出台相关政策和普及节水方面的知识以减少水资源的浪费。但降水量属于气候原因，难以预测，而且北京市属于温带季风型气候，降水量与季节有很大关系，所以能通过人力解决的水资源短缺风险因子为F1。

3 结论

水资源总量、农业用水量、工业用水量、第三产业及生活等其他用水量、污水处理量、降水量、人口数量都对北京市水资源短缺造成影响的因素。哲学上说凡事要分清主要矛盾和次要矛盾，因此应针对权重排名前三的因素来进行主要的分析。应用支持向量机方法得到农业用水量、第三产业及生活等其他用水量、降水量是在分析北京水资源短缺时最主要的因素。因此有关机构应针对这三个因素来制定对策。主成分分析法是一种多元统计分析技术，它具有和支持向量机一样的优点，即在面临维数灾难的时候，主成分分析法也可以将数据降维，以排除众多信息共存的互相重叠的信息，并将原变量进行转换，得到少数几个新的变量，根据其贡献率的高低来尽可能多的表达原变量的数据的结构而避免丢失信息。并且能够分析出某一主成分里面各项元素与该问题的正反相关性，同时能够根据这些元素的相关性分析出彼此的关联，从而发掘出结果表面现象下的本质问题所在。但是，该问题也存在一些纰漏，即某一元素在分析出的各个主成分中都有极大的相关性，就有可能会被重复计算和应用，影响结果的严谨性。

[1]徐劲力.支持向量机在水质评价中的应用.中国农村水利水电,2007年第3期

[2]魏歆、董小小、唐棣等.水资源短缺风险因子的筛选模型,数学的实践与认识,2011年23期

[3]李如忠 水质评价理论模式研究进展及趋势分析,合肥工业大学学报(自然科学版),2005年第4期

[4]衷平,沈珍瑶,杨志峰等.石羊河流域水资源短缺风险敏感因子的确定,干旱区资源与环境,2005年02期

[5]李坤峰,谢世友.基于主成分分析重庆水资源承载力影响因子评价《水科学与工程技术》2008年第S2期

[6]麻荣永,郑二伟,王魁等.基于主成分分析法的广西水资源可持续利用综合评价,广西大学学报(自然科学版)2008年第01期

[7]曹飞凤,袁伟,楼章华.富阳地区水资源自然支持力分析评价,自然资源学报,2007年第05期