二维动床数学模型在某地铁隧道冲刷深度研究中的应用

赵淳逸，金德钢，夏珊珊

（宁波市水利水电规划设计研究院，浙江 宁波 315192）

0 引言

近年来，随着社会经济的快速发展，人类活动与河流的相互作用日益加强，其关系也日益紧密。不断增多的涉水工程已成为影响河道冲淤的重要因素，这些工程破坏了河流的相对平衡，引起河流的再造床过程。与此同时，河道的冲淤演变又会对行洪排涝、涉水工程安全、通航及城市景观等产生影响。

作为城市公共交通系统的一个重要组成部分，轨道交通已成为缓解日益严峻的城市交通压力的重要手段，当轨道交通需跨越河道时，通常采用修建过江隧道的方式。在进行过江隧道规划设计时，隧道的埋深是关键参数之一，根据地铁盾构法施工技术要求，穿江隧洞顶部距河床底面之间的覆盖层厚度必须大于6m。合理的埋深不仅能确保隧道工程的建设和运行安全，也能大大降低工程投资和施工难度。

隧道工程合理埋深的确定主要取决于工程所在河段的最大冲刷深度。一般来说，河床的最大冲刷深度包括局部冲刷和一般冲刷两种类型，局部冲刷是指因阻水工程附近绕流作用，使床面附近产生漩涡淘刷河床所产生的冲刷；一般冲刷是指因河道单宽流量增大而产生的河床冲刷。在研究过江隧道最大冲刷深度时，考虑的是一般冲刷，即在特定水文条件下河床的极限冲刷深度。针对一般冲刷问题，国内很多学者进行了相关课题的研究，如史英标等［1］利用动床数值模拟和动床物理模型研究的手段，对钱塘江河口过江隧道河段极端洪水冲刷深度进行了研究，取得了较为满意的成果；谢东风等［2］以概念模式方法计算了淤泥质潮流深槽的最大深度，探讨了涨落潮流速、涨落潮历时、深槽淤泥质物质粒径、深槽顶底部原始深度、水道长度等因素对潮流深槽最大深度的影响。从国内以往的研究来看，对河道一般冲刷的研究方法主要包括河床演变分析、水沙数学模型和动床物理模型这3种。本文采用水沙数学模型计算的方法，以宁波市地铁2号线下穿姚江为例，预测工程线位河段的最大冲刷深度，并与一般冲刷经验公式计算结果相比较，为地铁工程合理埋深的确定提供科学依据。

1 研究区及工程概况①

1.1 流域概况

宁波市位于我国东部沿海，杭州湾以南，甬江流域为宁波市的主要水系，其主要河流包括姚江、奉化江和甬江干流，俗称“三江”（图1）。甬江由奉化江和姚江汇流而成：南源奉化江，其主流剡江发源于四明山东麓的秀尖山，至三江口的河长为93.4km；北源姚江发源于四明山北麓的夏家岭，至三江口的河长为107.4km。姚江、奉化江与甬江干流汇合于宁波市内三江口，甬江干流自三江口以下至镇海外游山入海，全长25.6km。1959年，在三江口上游3.3km建设姚江大闸，闸下河道仍为感潮河道，而闸上河道成为淡水河道。

宁波三江口潮位站多年平均高潮位为1.19m，平均低潮位为－0.49m，涨潮平均潮差为1.71m，落潮平均潮差为1.71m；奉化江多年平均径流量为16.855亿m3，姚江大闸多年平均排水量为11.39亿m3，甬江多年平均径流量为30.3亿m3。

1.2 泥沙特征

三江河道的泥沙分为海域来沙和陆域来沙两部分，随着流域治理的不断完善，陆域来沙相对减少，现状河道泥沙主要来源为外海细颗粒泥沙，泥沙运动主要以悬移质泥沙运动为主。河道含沙量横向变化特征是从河口至上游逐渐减小；纵向变化特征是表层水流含沙量小，底层水流含沙量大；季节变化特征是冬、春季含沙量大，而夏、秋季含沙量小［3］。

姚江市区河段上游建有姚江大闸，因此上游来沙较少，可忽略不计。姚江的泥沙以海域来沙为主。根据2010年7—8月全潮水文测验结果，市图书馆附近姚江断面涨潮平均含沙量为0.13kg／m3，落潮平均含沙量为0.1kg／m3，悬移质中值粒径为0.006 84～0.007 45mm，其中，粉沙含量为63.95%～78.39%，黏土含量为20.89%～35.97%。

据2010年10月地铁工程线位附近的底沙颗分试验结果显示，工程线位附近河床1＃垂线、2＃垂线及3＃垂线（垂线位置见下文图5）底泥的中值粒径分别为0.007，0.006 3和0.006 9mm。

1.3 河床演变特征

1959年姚江大闸建成后，姚江的潮流被截，甬江潮波变形，水沙平衡关系被打破，导致闸下至三江口段的河道迅速淤积，且淤积程度由闸下向河口递增。2000年以后，涉水工程增多，建筑物泥浆违规倾倒现象严重，使得河道淤积程度加大，潮流动力被进一步削弱。同时，三江口左岸咀边滩的淤长，又使姚江的进水断面缩窄，进潮量缩减，进一步促进了河道淤积。姚江大闸放水对下游河道具有一定的冲刷作用，但受放水量和放水时间的限制，闸下河段的冲刷量远小于回淤量，因此，姚江大闸至三江口河段总体处于单向淤积状态［4］。

1.4 工程概况

宁波轨道交通线网以主城区为核心，以跨三江、连三片、沿三轴为指导思想构成主体骨架，形成三主三辅6条线，总长230.1km，呈放射状的轨道交通线网，并在此基础上发展市域轨道交通。其中轨道交通2号线为SW－NE方向的基本骨干线，线路全长约50km，其中高架线28.8km，地面线1.1km，地下线20.1km，共设车站27座，并在鼓楼站和桃渡路站区间下穿姚江（图1）。

图1 三江河道流域及工程线位示意图Fig.1 General situation of the Sanjiang River Basin and the layout of engineering line

2 二维潮流泥沙数学模型建立

2.1 正交曲线网格生成

平面直角坐标系（x、y坐标系）下的非规则区域可以通过坐标转换的方式转换为规则区域（ξ，η正交

①赵淳逸，金德钢，夏珊珊，等.三江河道恢复性清淤工程相关课题研究总报告［R］.宁波：宁波市水利水电规划设计研究院，2011.曲线坐标），即由ξ＝ξ（x，y），η＝η（x，y）函数关系进行转化。正交曲线坐标系下的转换方程为［4］：

式中：Cξ和Cη为正交曲线坐标系下的拉梅系数，Cξ＝

式中，P和Q为网格调节因子，能对网格的疏密进行自动调节。但实际地形区域边界往往比较复杂，网格的密度既要反映河床平面变化，又要满足工程平面布置和尺度优化的要求，调节困难大。在实际应用中，通常先设初始网格，并做到边界纵向网格贴岸布置，横向网格与两岸基本垂直，并根据河床变化复杂程度和研究区域重要性适当加密纵、横向网格线，通过求解方程组实现网格系统的正交化。

上述方程组可采用有限差分法离散和TDMA技术求解。

2.2 水流运动基本方程

2.2.1 水流运动方程

弯曲河段水流模拟中应考虑弯道环流所引起的横向动量交换，正交曲线坐标系下弯曲河道水深平均的平面二维紊流模型控制方程为：

连续方程：

动量方程：

式中：C为阻力项，u、v为ξ、η方向流速分量，h为水位，H 为水深，g为重力加速度，σξξ、σηη、σξη和σηξ为应力项：

式中：νt为紊动粘滞系数。

2.2.2 悬移质不平衡输移方程

假定非均匀沙第i组泥沙同样遵循均匀沙的扩散规律，则第i组泥沙的扩散方程为：

式中：αi为悬沙中第i组泥沙恢复饱和系数；ωi为第i组泥沙的沉速；Si及S＊i为分组粒径的含沙量及挟沙力；εξ及εη为坐标系ξ及η方向的泥沙扩散系数，假定εξ＝εη＝νt。

2.2.3 河床变形方程

河床变形主要受悬移质作用，根据沙量守恒可得如下河床变形方程：

式中：Zb为河床高程，γ′s为泥沙淤积物干容重，α为恢复饱和系数。本次计算参照了陆永军等［5］在潮汐河口二维动床紊流模型中对恢复饱和系数取值的方法，在憩流时含沙量衰减过快引起河床过量淤积，计算时考虑了恢复饱和系数随涨、落潮的变化而变化，即当流速（流量）较小时，取值较小；当流速（流量）较大时，取值较大，就一般情况而言，淤积时取1.0，冲刷时取1.5。

挟沙能力S＊i通常与流速和水深等物理量有关，如刘家驹公式［6］和曹祖德公式［7］。本文采用率定得到的含沙量公式来近似代替挟沙力。根据三江流域各站点实测资料可知含沙量和流速的变化存在一定相位差（图1和图2）。

借鉴已有含沙量公式的推求方法［8］，设定三江流域的新含沙量公式形式如下：

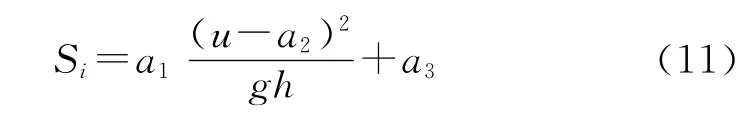
式中：a1、a2和a3为常量，依据不同区域选取不同的数值。新公式在三江流域各含沙量测站拟定结果较好，其中镇江和澄浪堰站位的含沙量计算值与实测值的相关系数分别为0.638 0和0.580 2（图3）。

图2 垂线平均含沙量与垂线平均流速时间序列图Fig.2 Time distribution of vertical mean sediment concentration and vertical mean velocity

图3 式（11）含沙量公式拟合结果图Fig.3 Fitting results of sediment concentration formula（11）

为了验证新的含沙量公式的合理性和可靠性，与甬江口现有的平均挟沙力公式［5］的拟合结果作对比。甬江口现有的平均挟沙力公式如下：

式（12）在镇海站和澄浪堰站的含沙量计算值和实测值的相关系数分别为0.591 9和0.450 1（图4），相关系数小于式（11）的相关系数。从一定程度上表明，式（11）对三江流域含沙量（挟沙量）的计算优于式（12），在研究区域具有一定的适用性。

图4 式（12）含沙量公式拟合结果图Fig.4 Fitting results of sediment concentration formula（12）

式中：P0bi和Pbi分别为时段初和时段末的床沙级配；ΔZi为冲淤深度；Em为床沙可动层厚度，其大小与河床冲淤状态、冲淤强度及冲淤历时有关。当处于单向淤积时Em＝ΔZi；当处于单向冲刷时，Em的限制条件是保证床面有足够的泥沙补偿。

2.3 边界条件

开边界采用强迫边界条件，进出口水边界采用实测潮位过程，z＝z（t），z指潮位。

数学模型进口给定断面紊动动能K、紊动动能耗散率ε沿河宽的分布，进口紊动动能耗散率按下式给定，即：

2.2.4 床沙级配调整方程

因本次研究所在河道泥沙属于细颗粒黏性沙，因此计算中不考虑推移质。在河床冲淤过程中，因床沙级配在不断调整，反过来影响水流挟沙能力，使冲淤向各自反面转化，因此床沙级配的调整对河床变形计算十分重要。

本研究中床沙级配调整方程采用下式计算：

式中：uj为进口断面节点纵向流速，Cf＝n2g／H1／3。

进口紊动黏性系数采用Laufer紊动黏性系数测量结果，即：

图5 模型河段计算水深图及水文测验布置图Fig.5 Calculated bathymetric chart in model and layout of the hydrologic test

由式（14）及（15）可推知进口断面紊动动能（K）分布：

陆边界的固壁边界采用法向通量为零的条件。

开边界给定含沙量过程线：

3 模型验证

3.1 计算范围及网格设置

计算范围为姚江从姚江大闸开始，奉化江从澄浪堰开始至甬江梅墟，河段长约17.6km。计算采用不等宽度网格，纵向网格宽度为10～20m，横向网格宽度为10～20m。在解放桥附近区域采用加密网格，加密网格纵、横向宽度均为10m。模拟流场的纵向网格节点数为524个，横向网格节点数为135个，模拟区域节点总数为70 740个。计算区域的水深值根据2009年9月最新的实测资料插值得到（高程床面绝对高程，即85黄海高程），具体如图5所示。

计算网格在岸线剧烈变化处边界附近网格正交性稍差，其它区域网格节点基本保持正交，正交误差为±3°。横向网格线遵循与两岸边界线垂直的趋势扭曲，纵向网格线呈凸岸密、凹岸疏的特点。

3.2 验证资料

地形资料采用2009年9月最新测量地形资料（测图比例为1∶2 000）。开边界条件采用2009年8月22日—23日和2009年8月28日—29日实测全潮水文测验资料。模型开边界共3条，分别是姚江大闸、澄浪堰和梅墟，水动力验证断面位于梅墟上游3.6km（图5）。

河床冲淤验证选取2008年12月应急清淤后至2009年8月河床地形资料作为计算的验证资料，2008年12月—2009年8月的河道潮位变化过程、河道含沙量变化过程作为计算的边界条件，模型对该时段的河床冲於变化过程进行模拟，计算出河段2009年8月的最终地形，并与2009年8月实测典型大断面资料进行对比，冲淤验证断面为姚江永丰桥和解放桥断面（图5）。

3.3 模型调试

模型在调试过程中，采用滩、槽不同糙率模拟流场阻力，经比选后确定河槽糙率一般取n＝0.018～0.020，滩地糙率取n＝0.03～0.05。为了比较合理地模拟滩地、桥墩等涉水建筑物的阻水作用，认为水深较浅时不过流，而在水深较大时，可以过流但受到阻力较大，所以采用建筑物所在网格高程较当地高0.5m，并将其槽率设为0.08～0.09，在这种边界条件下进行模型调试，反演计算区水文条件。在调试过程中考虑模拟河段水流交汇及河道弯曲的特点，选配动床糙率n＝0.014～0.017，根据实测河道横断面图对局部河槽地形进行了对位修改，更真实地反映河槽形态对过流和挟沙的影响，便于更合理地校验水位。曼宁糙率系数在计算中根据实测资料调整，一般在0.018～0.022之间，边滩和近岸糙率值较大，变化在0.035～0.045之间。在平面二维数学模型中，糙率n除反映河床粗糙度外，还包括了其它阻力因素对水流的综合影响，所以它已不是原有意义的糙率，应当把它看成是一个综合阻力的影响因子。

3.4 水动力验证

表1及图6分别给出了水动力验证断面潮位与流速过程计算值与实测值的比较，其中流速的正、负分别代表潮流的涨、落：落潮流速为正值，涨潮流速为负值。

表1 验证断面最高潮位与最大流速计算值Tab.1 Verification of the highest tide level and the maximum velocity

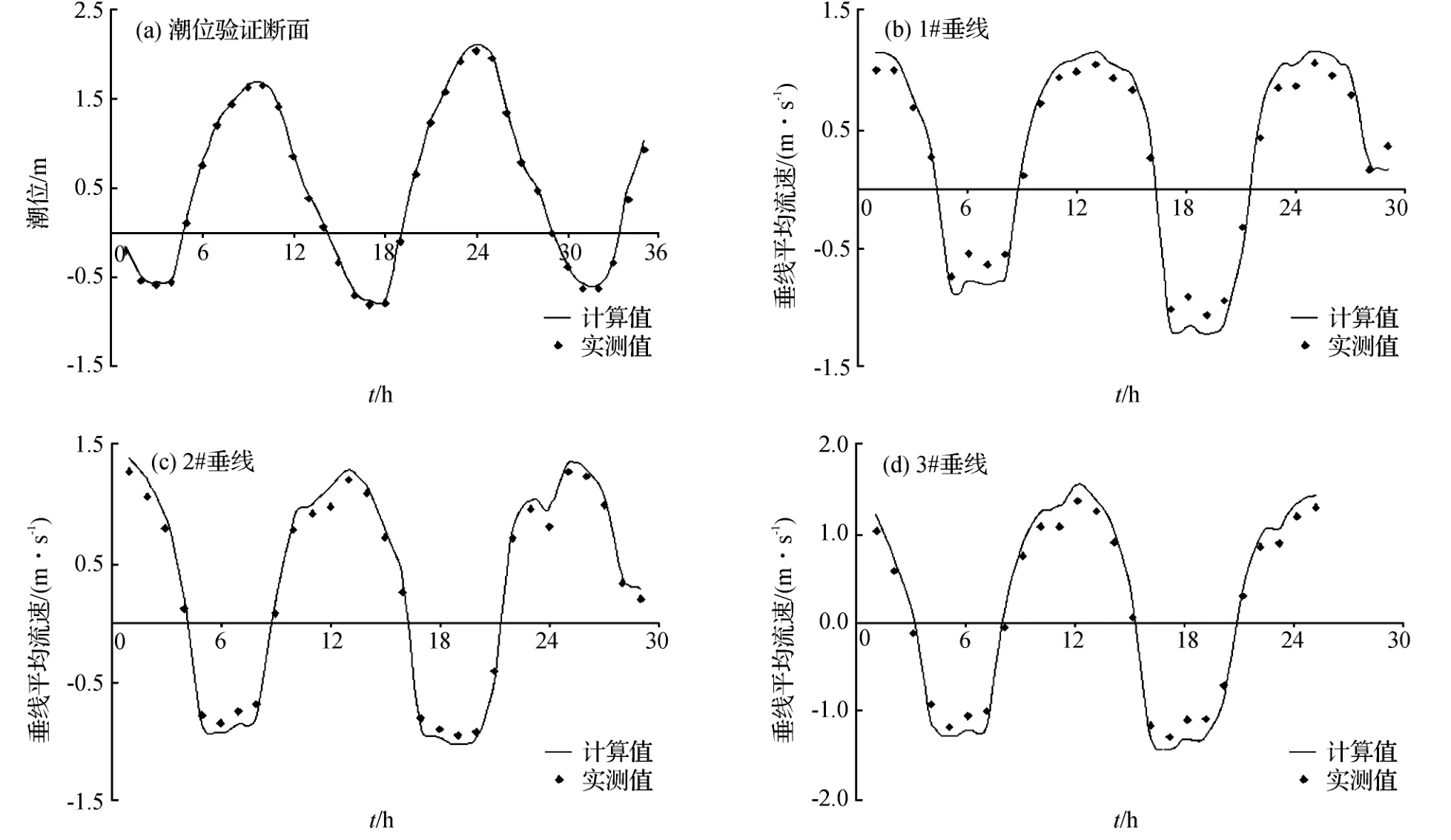
图6 潮位与垂线平均流速实测值与计算值对比Fig.6 Comparison between measured values and calculated values of tide level and vertical mean velocity

由图表可见，计算的潮位过程与实测潮位结果相当吻合，计算潮位与实测潮位的偏差最大仅0.03m；计算流速结果与实测值偏差一般小于0.03m／s，平均误差为0.03m／s。总体来说，模型计算结果与实测结果基本吻合。

3.5 流场

模型根据实测水文条件，模拟了工程线位附近河段涨、落潮流场，其中涨急和落急计算流场如图7所示：断面流速分布与河槽断面形状相近，深槽附近流速较大，近岸流速较小，弯道水流特性明显。

图7 计算所得流场图Fig.7 Calculated flow field

3.6 河床冲淤验证

3.6.1 典型断面冲淤形态验证

2009年8月姚江典型断面计算地形如图8所示。由图可见，各典型断面地形高程的计算值与实测值基本接近，模型计算结果基本合理。

3.6.2 冲淤量验证

表2为2008年12月至2009年8月姚江闸下河段的计算冲淤量与实测冲淤量的对比，由表可见，实测河段淤积约239 571.0m3，而计算淤积量约213 674.2m3，其绝对误差为25 896.8m3，相对误差为10.8%，各河段计算冲淤量的误差在10%左右。可见，无论是河段总淤积量，还是边滩局部淤积量，计算值与实测值误差满足工程计算规范允许误差30%的规定要求。

图8 断面冲淤验证Fig.8 Verification of erosion and siltation

表2 姚江河段泥沙冲淤量验证Tab.2 Verified volume of scouring and siltation of the Yaojiang River reaches

4 成果分析

4.1 计算水文组合条件

本次计算条件是根据流域水文特性、下垫面条件、河道设防标准及洪潮组合分析所确定：

（1）流域水文特性：工程河段受上游径流、下游潮汐的共同作用，计算河段上边界需考虑洪水频率，下边界需考虑潮汐频率。

（2）下垫面条件：随着甬江流域防洪治涝工程体系的进一步完善，相同洪潮遭遇组合条件下，现状和规划流量－水位条件亦将发生变化，鉴于地铁工程的安全性和重要性，应同时考虑现状和规划两种工况。

（3）河道设防标准：本次模拟范围河段堤防已按规划100a一遇防洪（潮）标准建设。

（4）洪潮组合分析：洪潮组合分析主要研究多个水文变量相互遭遇组合的可能性，根据已经发生和可能发生的样本的出现几率，研究它们相遇的概率。本工程所在的姚江河段在下游三江口与奉化江汇合经甬江入海，因此洪潮组合遭遇包括洪水组合遭遇和洪潮组合遭遇两方面。其中洪水组合主要根据已发生的暴雨情况来分析2条支流的洪水遭遇情况，现有资料分析表明当甬江流域发生大洪水时，上游2条支流不发生同频率洪水，而在一般洪水时，两支流洪水可能会同频率组合；洪潮组合考虑到甬江流域在洪潮遭遇方面不存在明显的规律，它们两者之间处于相互独立的地位，从近52a（1956—2007年）统计资料分析，未出现低频率洪水与低频率潮位的组合情况，低频率洪水与高频率潮位出现几率较多。

根据以上原则，拟定现状和规划条件各3组共6组水文组合条件（表3）。

4.2 工程线位附近最大冲刷深度分析

表3给出了不同工况及水文组合条件下工程线位附近河床的最大冲刷深度计算结果。

由计算结果可以看出，无论是在现状还是规划条件下，地铁2号线线位附近的最大冲刷深度都取决于姚江流域洪水频率的大小，在相同流域下垫面条件下，姚江洪水频率越小，形成的冲刷深度也越大。规划和现状条件下的最大冲刷都发生在姚江100a一遇洪水＋奉化江20a一遇洪水＋甬江5a一遇小潮的工况，相应的冲刷深度分别为1.87m和1.11m，冲刷后断面的最深河底高程分别为－5.43m和－4.67m，由于规划状态下姚江二闸分洪，同频率条件下现状的冲刷深度要大于规划状态。

表3 不同工况及水文组合条件下工程线位附近河床最大冲刷深度统计表Tab.3 Statistical table of the greatest scour depth of riverbed near engineering line under different working and hydrological conditions m

4.3 工程线位附近断面冲刷形态分析

如图9所示，在各不利洪潮遭遇组合条件下，姚江大闸泄流对工程线位附近河床产生冲刷，冲刷的断面分布特征表现为主槽的冲刷相对较大，而边滩的冲刷相对较小；因工程河段河道基本顺直，深泓大致居中，冲刷后河道宽深比减小，但主流动力轴线横向摆动幅度较小，最大冲深位置位于现状河道深泓附近。

4.4 工程线位附近冲刷过程分析

如图10所示，在计算的初始时间段（0～40h），姚江大闸没有泄流或泄流量较小，姚江闸下河段冲刷很小，在现状方案一和方案二水文组合条件下还发生强度不大的淤积；从40h开始，随着大闸泄洪流量的增大，工程线位附近河床冲刷深度逐渐加大，冲刷强度随断面水位－流量关系的变化而变化；140h以后，冲刷强度逐渐减小并趋于稳定。

图9 各工况方案组合条件下工程线位附近断面冲淤形态对比图Fig.9 Scour and siltation of cross－sections near engineering line under different working and hydrological conditions

图10 现状工况下各水文组合条件工程线位附近最深点冲刷过程线图Fig.10 Scouring process of the deepest point near engineering line under different hydrological conditions of current situation

4.5 公式法冲刷对比分析

为了比较和校核数学模型的计算成果，获得不同研究手段下的冲刷深度，本研究还采用经验公式对地铁2号线线位附近河道的冲刷深度进行了计算。

4.5.1 公式的比较与选择［9］

天然河道中的冲刷，目前还没有一个完整的描述河床冲淤变化的表达式。一般情况下可采用规范推荐的经验公式结合实测资料，进行冲刷和淤积分析计算，现有公式主要有集中水流局部冲刷坑lacey公式、谢鉴衡公式、铁路工程水文勘测设计规范公式、包尔达可夫公式等。鉴于工程下穿姚江河段断面水流含沙量较小，泥沙的粒径较小，属于黏性土，对于河床的一般冲刷，可采用铁路工程水文勘测设计规范3.6.3－1公式，计算结果较准确。

4.5.2 冲刷深度的计算结果

最大冲刷深度计算按《铁路工程水文勘测设计规范》（TB10017－1999）［10］拟定的黏性土河床的桥下一般冲刷公式计算，轨道交通工程的冲刷计算是为了得到河床冲刷的极限深度，因此可以按照河槽部分的计算公式来进行计算：

式中：hp为一般冲刷后的最大水深（单位：m）；hmc为河槽部分最大水深（单位：m）为河槽部分平均水深（单位：m）；Bc为河槽部分桥孔过水净宽（单位：m），本次计算根据实测断面资料，取Bc＝230～250m；Qc为河槽部分通过的设计流量（单位：m3／s），本次计算Qc取各洪潮遭遇组合方案下断面的最大洪峰流量；IL为冲刷范围内黏性土样的液性指数，其范围为0.16～1.19，根据现场取样分析，姚江河床质主要为软塑体，故取液性指数为0.8；A为单宽流量集中系数，可按公式计算，其中：Bd为造床流量时的河宽；为平均水深，可按平滩水位计算对于河床宽浅的游荡河段、变迁河段；当Bd值过大和平滩水位不能确定时，可采用，即A≤1.8，本次计算根据实测断面资料取A＝1.2。

根据上述计算公式，选取恢复性清淤工程设计断面为初始河床地形，不同洪潮遭遇组合方案下，现状条件下，轨道交通2号线下穿姚江断面处最大冲刷水深计算结果见表4。

表4 用经验公式计算的工程线位附近河床冲刷结果（现状）Tab.4 Scour results of riverbed near the engineering line calcuated by empirical formula（current situation）

从上表可以看出，姚江闸下河段的最大流量主要受大闸泄流的影响，低频率洪水作用下工程线位附近的最大流量也相应增大，相应的河床冲刷深度也越大。计算结果表明，现状条件下，在遭遇各洪潮组合水文条件时，极限冲刷深度为1.97m，对应的最大流量为1 024.5m3／s，出现在姚江100a一遇洪水＋奉化江20a一遇洪水＋甬江5a一遇小潮的工况，相应的河床冲刷底高程为－5.53m，与模型计算成果相差0.1m。

数模计算的条件是基于一定的潮位－流量过程，所获得冲刷结果是冲刷的沿程变化及断面分布，而经验公式计算的条件是选取某一潮位－流量过程中的不利时刻，所获得的冲刷结果是该时刻条件下冲刷的最大值，从地铁工程的重要性及安全性角度，应选取数模和经验公式计算结果的较大者作为极限冲刷深度。

5 结论

在感潮河段建设隧道工程，隧道的合理埋深是工程设计的重要参数之一，然而由于工程河段的水流泥沙运动条件复杂，河道冲淤变幅大，影响河道冲淤的影响因素多。本文以宁波市地铁2号线下穿姚江工程为例，应用平面二维水沙数学模型、经验公式计算、综合分析等多种技术手段，对过江线位附近河段的最大冲刷深度进行了探讨：

（1）感潮河段河道的最大冲刷深度与来水来沙条件、水利工程调度运行及下垫面条件等密切相关，在研究最大冲刷深度的计算条件时，应综合考虑这些影响因素，拟定合理的计算工况。

（2）以平面二维k－ε紊流模型为理论基础，对各种不利水文组合条件下河道的最大冲刷深度进行了研究，结果表明，洪水频率越小，工程线位附近河段的最大冲刷深度愈大，冲刷发展呈先加快后减慢的态势。

（3）在数模计算的基础上，根据工程河段的特性，对现有冲刷计算经验公式进行了比选，利用冲刷公式计算各种工况下的极限冲刷深度，并与数模计算结果相对比，因数模和经验公式计算原理及计算条件不同，两种手段的计算结果存在差异，在实际工程应用中，应根据具体情况进行分析取用。

（References）：

［1］SHI Ying－biao，LU Hai－yan，YANG Yuan－ping，et al.Prediction of erosion depth under the action of the exceptional flood in the river reaches of a tunnel across the Qiantang estuary［J］.Advance in Water Science，2008，9（2）：685－692.

史英标，鲁海燕，杨元平，等.钱塘江河口过江隧道河段极端洪水冲刷深度的预测［J］.水科学进展，2008，9（2）：685－692.

［2］XIE Dong－feng，GAO Shu.Modeling maximum scour depths of tidal channels with mud substrate in shallow marine environments［J］.Journal of Marine Sciences，2006，24（3）：10－20.

谢东风，高抒.淤泥质潮流深槽最大冲刷深度的一个概念模型［J］.海洋学研究，2006，24（3）：10－20.

［3］YAN Wen－wu.Water and sediment characteristics and their scou－ring and silting law in the three rivers of Ningbo［J］.Hydro－Science and Engineering，2011，33（4）：143－148.

严文武.宁波三江河道水沙特性及冲淤变化规律［J］.水利水运工程学报，2011，33（4）：143－148.

［4］JIN De－gang，ZOU Cang－guo，YANG Cheng－gang.The solution and application of 2Dwater flow and soil model on mobile bed at central city part of Fenghuajiang River［J］.Journal of Marine Sciences，2008，26（4）：29－34.

金德钢，邹长国，杨成刚.奉化江中心城区段二维动床水流泥沙数学模型的求解及应用［J］.海洋学研究，2008，26（4）：29－34.

［5］LU Yong－jun，YUAN Mei－qi.2－D Mobile bed turbulent model for tidal funnel［J］.Advances in Water Science，1998，9（2）：151－158.

陆永军，袁美琦.潮汐河口二维动床紊流模型［J］.水科学进展，1998，9（2）：151－158.

［6］LIU Jia－ju.Calculation and prediction of siltation in the approach channel to Lianyun Harbour［J］.Hydro－Science and Engineering，1980，2（4）：32－37.

刘家驹.连云港外航道的回淤计算及预报［J］.水利水运科学研究，1980，2（4）：32－37.

［7］CAO Zu－de，LI Bei，KONG Ling－shuang.Carrying capacity for a wave－current coexistent system［J］.Journal of Waterway and Harbor，2001，22（4）：151－155.

曹祖德，李蓓，孔令双.波、流共存时的水体挟沙力［J］.水道港口，2001，22（4）：151－155.

［8］YU Die－shuang，LI Rui－jie，FENG Qing，et al.Characteristics of sediment concentration variations in offshore area south of the Oujiang estuary［J］.Journal of Waterway and Harbor，2013，34（1）：7－12.

余蝶双，李瑞杰，丰青，等.瓯江南口外浅滩含沙浓度特征［J］.水道港口，2013，34（1）：7－12.

［9］CHANG Huai－min，ZHAN Sheng－wen.Scouring depth analysis of pipeline crossing through Yangtze River using empirical formulas［J］.Petroleum Engineering Construction，2007，33（10）：16－18.

常怀民，詹胜文.经验公式计算某管道长江穿越冲刷深度的分析［J］.石油工程建设，2007，33（10）：16－18.

［10］Ministry of Railways of the People's Republic of China.TB10017—1999Hydrological specifications for survey and design of Railway Engineering［S］.1999.

中华人民共和国铁道部.TB10017—1999铁路工程水文勘测设计规范［S］.1999.