FrFT-OFDM系统的低复杂度峰均功率比抑制技术研究

2014-05-22时鹏飞蒋政国

电子与信息学报 2014年1期

赵越王腾陶然时鹏飞蒋政国

赵越王腾陶然时鹏飞蒋政国

(北京理工大学信息与电子学院北京 100081)

针对基于分数阶Fourier变换的OFDM系统(简称FrFT-OFDM系统)的高峰均功率比(PAPR)问题，该文提出一种低复杂度的峰均比抑制算法。通过对随机相位序列采用周期延拓至FrFT-OFDM符号长度，相位因子加权后与子载波调制前的数据相乘的方式，实现对高峰均比的有效抑制。该算法只需要一次逆离散分数阶Fourier变换(IDFrFT)，所有备选信号直接通过时域chirp圆周移位的加权和得到。仿真结果表明，当备选信号个数相同时，该算法与选择映射(SeLecting Mapping, SLM)算法的PAPR抑制性能相当，比部分传输序列(Partial Transmit Sequence, PTS)算法具有更好的PAPR抑制性能，同时，该算法较SLM和PTS算法的运算量降低。

正文频分复用；分数阶Fourier变换；峰均功率比；低复杂度

1 引言

由于在时频双弥散信道中，OFDM系统中子载波间的正交性容易受到破坏，从而形成严重的子载波间干扰。为了克服这一问题，文献[1]提出了FrFT- OFDM系统，并得出在快速时变信道中FrFT- OFDM系统比传统OFDM系统具有更好的传输性能；同时，FrFT的计算复杂度和FFT相近，容易实现，所以FrFT-OFDM系统具有很大的应用价值。

然而，作为多载波传输系统，FrFT-OFDM系统同样存在高峰均功率比问题，这一问题直接影响系统的运行成本和效率，是该技术不可忽视的问题之一。文献[2]对FrFT-OFDM系统的PAPR分布进行了理论推导与仿真验证，并得出随着子载波个数的增加，FrFT-OFDM系统的PAPR分布和传统OFDM系统的PAPR分布趋于一致，即对应不同阶次的FrFT-OFDM系统的PAPR分布趋于一致。目前，FrFT-OFDM系统的峰均比抑制算法仅仅是将传统OFDM系统的算法直接应用到该系统中，传统OFDM系统的峰均比抑制算法有：限幅法[3]、选择映射法(SLM)[4]、部分传输序列法(PTS)[5]、有效星座扩展法(ACE)[6,7]、压缩扩展法[8,9]、子载波预留法[10]等。文献[11]将传统的SLM法和PTS法分别应用于FrFT-OFDM系统，系统的峰均比特性有了明显改善，但是这两种算法存在计算复杂度大的问题。虽然文献[12]针对传统OFDM系统中PTS算法运算量大的问题提出了CSPS(Cyclically Shifted Phase Sequences)和OCSPS(Optimised CSPS)算法，但是由于分数阶Fourier变换chirp周期性[13]的存在，该算法并不能直接应用到FrFT-OFDM系统。

基于以上问题，本文对CSPS和OCSPS算法进行了改进，提出一种适用于FrFT-OFDM系统的低复杂度的峰均比抑制算法，该算法基于分数阶随机相位序列和分数阶圆周卷积定理，有效降低了算法运算复杂度。

2 FrFT-OFDM系统模型

FrFT-OFDM系统模型如图1所示。FrFT- OFDM系统用chirp基代替正弦基作为子载波基信号，系统利用IDFrFT和DFrFT进行子载波的调制和解调，子载波调制信号表示为(这里将幅度进行了归一化)[14]

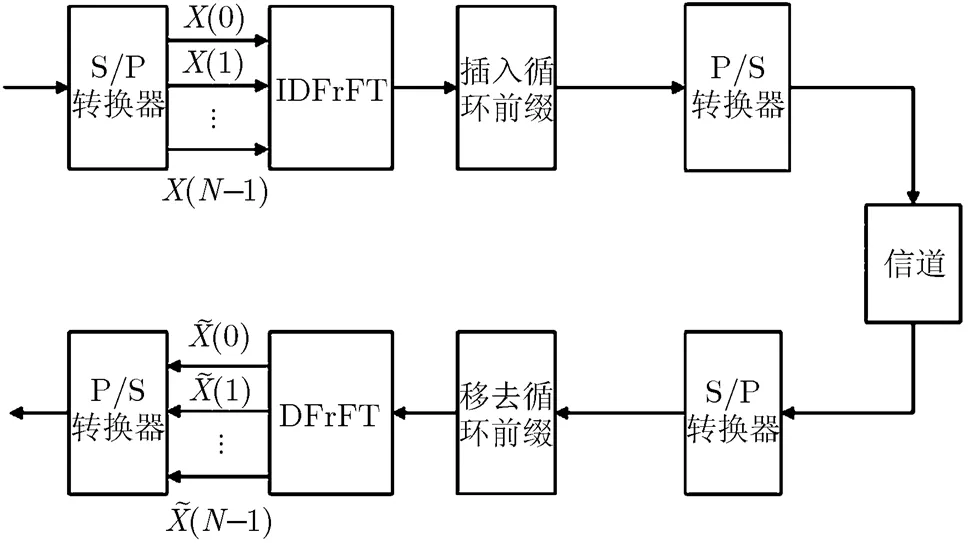
图1 FrFT-OFDM系统原理图

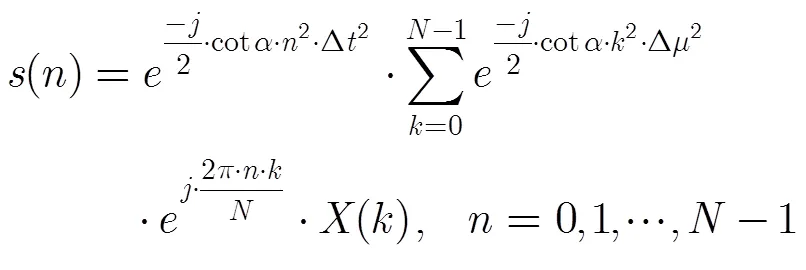
3 低复杂度的峰均功率比抑制算法

3.1 设计分数阶随机相位序列

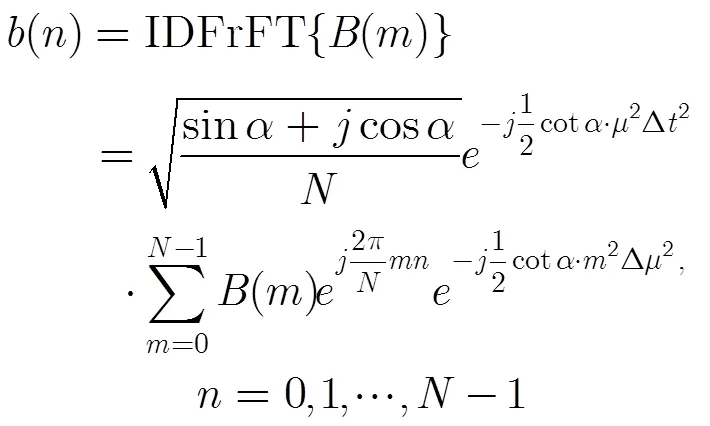
将式(2)和式(3)代入到式(4)中，得到

3.2 低复杂度峰均比抑制算法

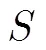
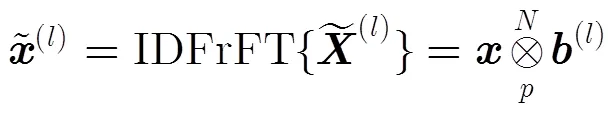
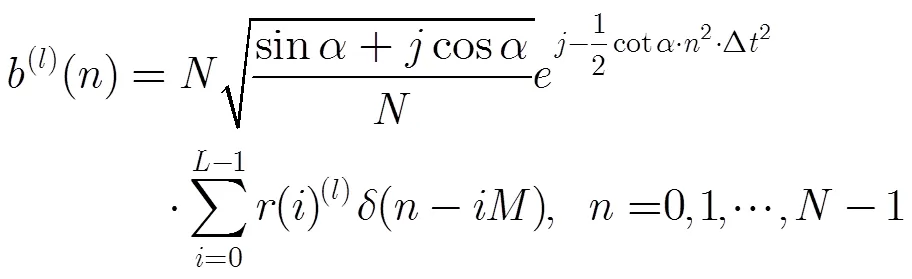
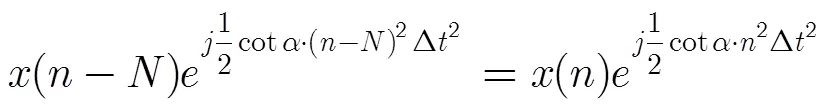
图2 算法原理图

根据上面的描述，现对算法的步骤总结如下：

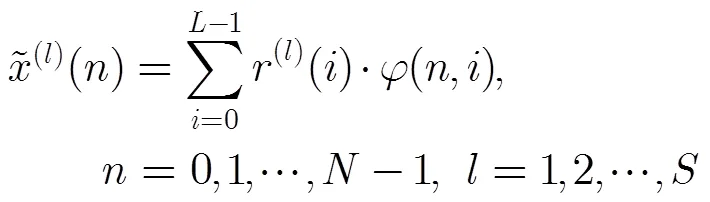
3.3 运算复杂度对比分析

表1 SLM, PTS和本文算法的运算复杂度

表2 具体参数下3种算法的运算复杂度

4 仿真验证

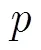
图3 时3种算法的PAPR抑制效果

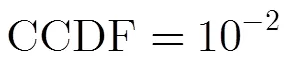
5 结束语

[1] Massimiliano M. A Multi-carrier system based on the fractional Fourier transform for time-frequency-selective channels[J]., 2001, 49(6): 1011-1020.

[2] Ju Y, Barkat B, and Attallah S. Analysis of peak-to-average power ratio of a multicarrier system based on the fractional Fourier transform[C]. 2004 9th IEEE Singapore International Conference on Communication System, Singapore, 2004: 165-168.

[3] Wang Yong-chao and Luo Zhi-quan.Optimized iterative clipping and filtering for PAPR reduction of OFDM signals[J]., 2011, 59(1): 33-37.

[4] Jeon Hyun-bae, No Jong-seon, and Shin Dong-joon. A low-complexity SLM scheme using additive mapping sequences for PAPR reduction of OFDM signals[J]., 2011, 57(4): 866-875.

[5] Ku Sheng-ju and Wang Chin-liang. A new side-information free PTS scheme for PAPR reduction in OFDM systems[C].2012 IEEE 8th International Conference on Wireless and Mobile Computing, Networking and Communications, Barcelona, 2012: 108-112.

[6] Niranjan M and Srikanth S. Adaptive active constellation extension for PAPR reduction in OFDM systems[C]. IEEE International Conference on Recent Trends in Information Technology, Chennai, Tamil Nadu, 2011: 1186-1189.

[7] Jeon Hyun-bae, No Jong-seon, and Shin Dong-joonA new PAPR reduction scheme using efficient peak cancellation for OFDM systems[J]., 2012, 58(4): 619-628.

[8] Wang Y, Wang L-H, Ge J-H,.. An efficient nonlinear companding transform for reducing PAPR of OFDM signals[J]., 2012, 58(4): 677-684.

[9] Wang Dong, Zou Nian-yu, Cui Gao-feng,.. Companding scheme for peak-to-average power ratio reduction in optical orthogonal frequency division multiplexing systems[J]., 2012, 19(6): 371-375.

[10] Park Kang-woo and Park In-cheol. Low-complexity tone reservation for PAPR reduction in OFDM communication systems[J]., 2012, 20(10): 1919-1923.

[11] Xie Dan, Yang Shou-yi, Qi Lin,.. PAPR reduction of FRFT-based MB-OFDM ultra wide band signals[C]. WiCOM’08, 4th International Conference on Wireless Communications, Networking and Mobile Computing, Dalian, 2008: 1-4.

[12] Lu G, Wu P, and Aronsson D. Peak-to-average power ratio reduction in OFDM using cyclically shifted phase sequences[J]., 2007, 1(6): 1146-1151.

[13] Tomaso E, Peter K, and Gianfranco C. Unified fractional Fourier transform and sampling theorem[J]., 1999, 47(12): 3419-3423.

[14] Chen En-qing, Tao Ran, and Meng Xiang-yi. The OFDM system based on the fractional Fourier transform[C]. 2006 International Conference on Innovative Computing, Information and Control, Beijing, 2006: 14-17.

[15] 陶然, 邓兵, 王越. 分数阶Fourier变换的原理与应用[M]. 北京: 清华大学出版社, 2009: 185-198.

Tao Ran, Deng Bing, Wang Yue. Fractional Fourier Transform and Its Applications[M]. Beijing: Tsinghua University Press, 2009: 185-198.

[16] Pei S C and Din J J. Closed-form discrete fractional and affine Fourier transform[J]., 2000, 48(5): 1338-1353.

赵越：女，1987年生，硕士生，研究方向为OFDM系统PAPR抑制、信道估计及均衡等关键技术的研究.

王腾：男，1988年生，博士生，研究方向为通信信号处理理论、扩频通信抗干扰、宽带与超宽带信道估计及均衡等关键技术的研究.

陶然：男，1964年生，教授，博士生导师，研究方向为分数阶傅里叶变换的理论与应用、雷达系统与技术、通信系统.

Peak to Average Power Ratio Reduction with Low Computational Complexity in FrFT-OFDM System

Zhao Yue Wang Teng Tao Ran Shi Peng-fei Jiang Zheng-guo

(,,100081,)

This paper proposes a low-complexity Peak to Average Power Ratio (PAPR) reduction method inOrthogonal Frequency Division Multiplexing (OFDM) system based on the Fractional Fourier Transform (FrFT). The method reduces PAPR effectively through periodic extension of random phase sequence to the length of FrFT-OFDM symbol,weighting it with phase factors and multiplying transmitted data vector.Only one Inverse Discrete Fractional Fourier Transform (IDFrFT) operation is performed in the proposed method, and the signal candidates can be calculated in time domain via weighted summation of the chirp circularly shifted FrFT-OFDM symbols. The simulation results show that, in the case that all the methods have 32 candidates, the proposed method hasalmost the same performance, when compared with the SeLecting Mapping (SLM) and performs even better than the Partial Transmit Sequence (PTS). More importantly, the proposed method has lower computational complexity compared with SLM and PTS.

Orthogonal Frequency Division Multiplexing (OFDM); Fractional Fourier Transform (FrFT); Peak to Average Power Ratio (PAPR); Low-complexity

TN914

1009-5896(2014)01-0246-04

10.3724/SP.J.1146.2013.00323

2013-03-15收到，2013-06-13改回

北京市自然科学基金(4112051)和教育部博士点基金优先发展领域(20121101130001)资助课题

赵越 zyozhm@163.com