基于最小熵理论和未确知测度理论的泥石流敏感性分析

单 博，陈剑平，王 清

（吉林大学 建设工程学院，长春 130026）

1 引 言

泥石流是一种常发生在山区，由水、土壤或岩体和汽组成的碎屑流，常具有形成过程复杂、暴发突然、来势凶猛、历时短暂、破坏力极大等特点[1]。其侵蚀能量和发生频率常取决于泥石流流域的地质、地形、气象和植被等条件[2]。由于泥石流具有高密度、高流动性和高流速，具有极大的破坏性，往往对环境、经济及人类的生命和财产安全构成极大的威胁，因此，从减灾防灾的角度来说，对泥石流的敏感性分析显得尤为迫切[3]。

近年来，多种方法或模型已被应用到泥石流危险度或敏感性分析中，它们主要可以被划分为两种类型：半定量和定量分析方法。层次分析法作为其中一种半定量分析方法已被应用到泥石流危险度评价领域[4]。值得关注的定量方法主要包括数据统计分析法[3,5－6]、人工神经网络[7－8]、遗传算法[9]、证据权法[10]和可拓学理论[11]等。数据统计分析法，即假定过去泥石流诱发因素与未来泥石流诱发因素相同，被认为非常适于对大规模和复杂地区的泥石流进行危险度或敏感性分析。人工神经网络和遗传算法不能提供客观和稳定的输出，因为其评价结果取决于输入层参数的设置。可拓学理论在解决矛盾和不兼容问题方面有着无比的优越性，已被广泛应用到泥石流敏感性分析等众多领域。总之，以上方法对于泥石流危险度评价或敏感性分析的发展起到了很好的推动作用。但泥石流的发生是一个受到物源条件、地形条件和以一些诱发因素控制的极其复杂的地质过程，其中包括了很多的不确定和隐蔽因素，以上文献方法未曾考虑或考虑不够全面，而未确知测度理论综合考虑这些不确定信息进行综合评价，这就为泥石流的危险度评价提供了一个新的思路。

在自然科学和工程技术研究中，往往存在着很多不确定的信息，这些信息可以归结为模糊性、随机性和未确知性。对于随机性和模糊性数据已经提出了统计数学和模糊数学等理论，而未确知信息的研究相对滞后。未确知信息及其数学处理理论最早由王光远[12]于1990年提出，以此为基础，刘开第等[13]提出了未确知数学理论，目前该理论已经被广泛应用于工程地质学科的很多领域[14－15]。本文即鉴于该理论，将其引入到泥石流敏感性分析中。

目前在各领域确定权重的方法主要有主观和客观两种方法之分，每种方法都有各自的优点和缺点[11]。最小熵分析原理作为一种新的客观的数据分析方法，在优选主要影响因子、确定各因子对系统的贡献率及计算因子权重方面有着无可比拟的优越性，近年来已被广泛应用到地质灾害评价领域中[16]。Chen等[16]将其应用到台湾地区泥石流影响因子优选及危险度评价，取得了不错的效果，验证了最小熵分析原理基于有限的实例样本进行数据分析的可靠性。因此，本文基于最小熵分析原理来确定各影响因子对泥石流敏感性的贡献率和权重。

2 最小熵分析原理

通过研究每个子模型对系统的解释度，即研究哪些子模型能最好地解释所研究泥石流系统，即可求出每个变量对系统的贡献率，进而可确定主要变量及其权重值。

对于每个子模型，可以运用Logit模型关联各变量之间的响应。如果变量与目标判定结果关联，则用二进制结果“1”表示；若不关联，则用“0”表示。Logit模型如下式：

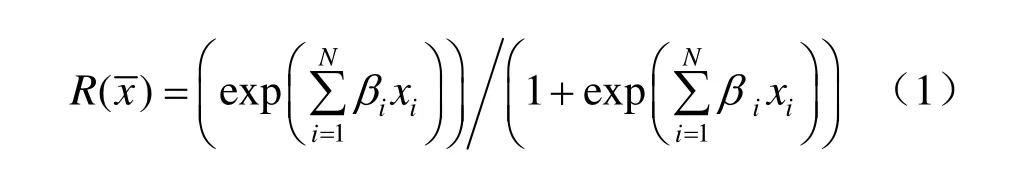
归一化式（1）后，可以得到包含所有变量的给定子集的响应概率分布函数：

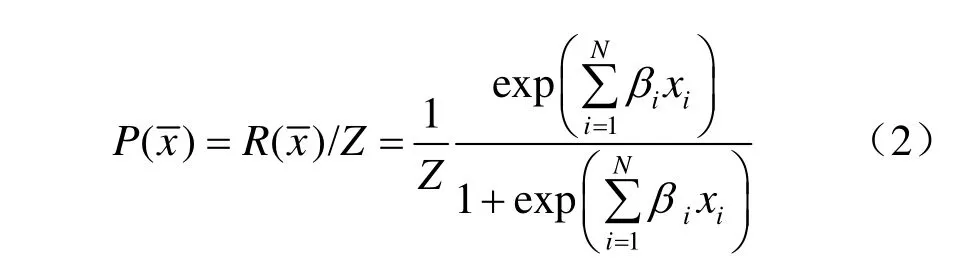
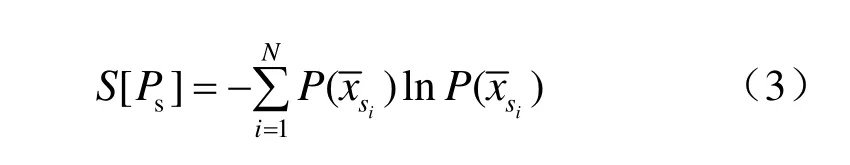
对所有子模型按计算所得的熵值大小进行排序，根据某种判定规则选取熵值最小的前M个子模型，称之为有效子模型，统计有效子模型中每个变量出现的频率，确定其对系统的贡献率。出现的频率愈大，说明对系统的贡献也就愈大，据此就可以确定系统的主要变量。

3 未确知测度理论

3.1 单指标测度评价矩阵

若 μijk=μ(Xij∈ Ck)表示测量值Xij属于第k个评价等级 Ck的程度，若μ满足0≤μ(Xij∈ Ck)≤1，且满足可加性和归一性准则，则称μ为未确知测度，简称测度。称矩阵为单指标测度评价矩阵：

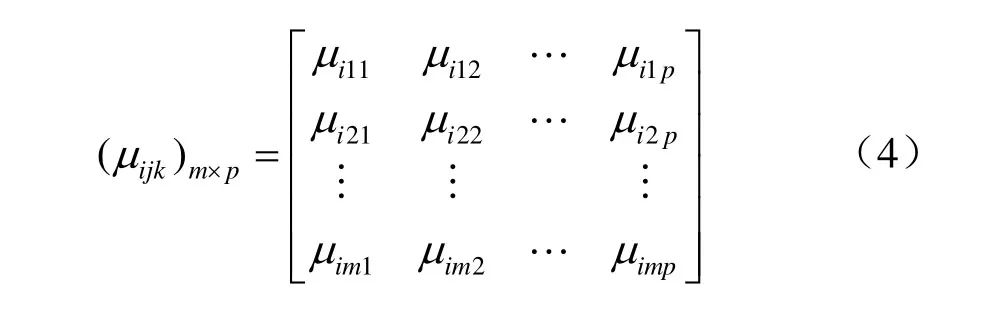
3.2 多指标综合测度评价矩阵

令 μik=μ(Ri∈ Ck)表示泥石流沟Ri属于第k个评价等级 Ck的程度，则

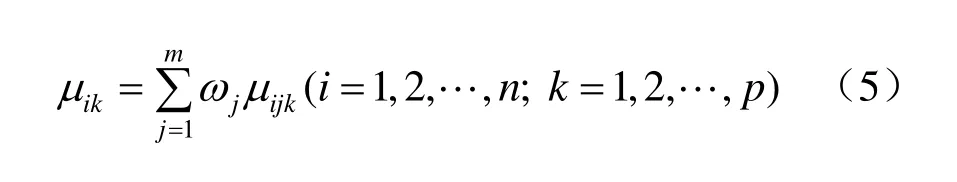
式中：ωj为评价指标Xj在评价体系中所占的?权重值。多指标综合测度评价矩阵可表述为

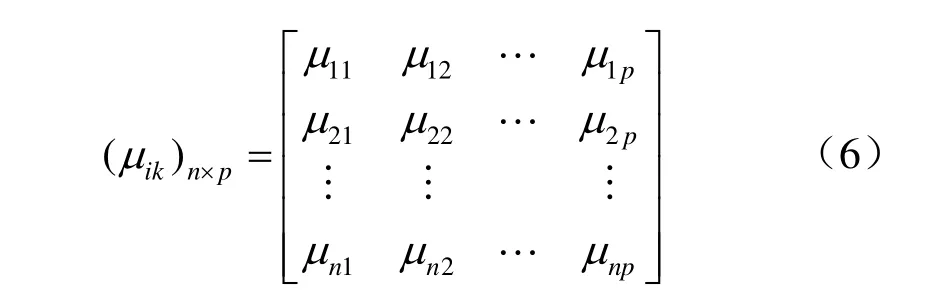
3.3 置信度识别准则分析敏感性

为了对待评价的泥石流沟做出最终的评价结果，采用置信度识别准则。若评价空间U有序，且C1＞C2＞C3＞… Cp，设λ为置信度（λ≥0.5，常取 0.6 或 0.7）[14－15]，则有

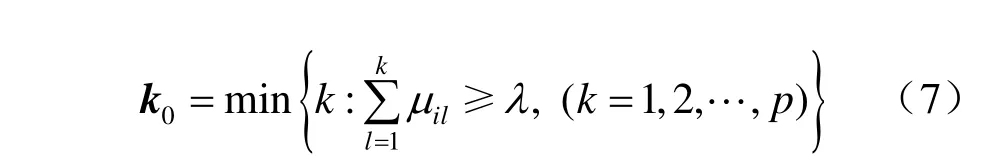
那么，可认为泥石流沟 Ri的敏感性等级属于第k0个评价等级 Ck0。

4 研究区概况

研究区位于云南省和四川省交界处金沙江乌东德水电站库区，山高谷深、地形陡峭、河流深切、断层交错、岩层破碎、重力侵蚀严重、地质构造活动强烈，是我国地质灾害频发的地区之一。

库坝区一带发育有数条区域性的活动断裂，库坝区内的地质条件较为复杂。如呈南北走向的安宁河断裂、元谋断裂和德干断裂等晚更新世以来活动频繁，甚至一些地震的发生就与断裂构造的活动有一定的相关性。

研究区位于南亚热带及中亚热带，属典型的亚热带季风气候。山高谷深，气候垂直变化强烈。河谷属于干热河谷，河谷内日降雨集中，蒸发量巨大，导致流域内水系结构复杂，为物源的运输提供了通道。此外，河谷地表温度可达70～75 ℃，远远高于气温，巨大的温差使岩土体的物理风化作用强烈。

从地形来看，研究区海拔分布在900～3500 m之间，山坡的平均坡度多分布在 30°～45°。泥石流主沟两侧山坡坡度均较大，最大可达60°，部分泥石流沟主沟呈“V”字型，主沟的平均比降为0.1～0.4，随处可见崩滑现象，松散物源充足，为泥石流的发生提供了有利条件。

5 泥石流敏感性分析

5.1 泥石流敏感度分析因子体系

泥石流的影响因子主要有地质、地貌、水文、气象、植被和人类活动等。根据前人的研究[11,17－21]，本文选取了9个主要因子，即X1为单位面积松散物源量（104m3/m2），X2为坡度（°），X3为主沟平均比降，X4为流域面积（km2），X5为形状因子，X6为主沟长度（km），X7为主沟床弯曲系数，X8为沟壑密度（km/km2），X9为植被覆盖率（%）。各因子的指标值见表 1。各因子的选取依据描述如下：

（1）X1单位面积松散物源量愈大，松散物源体抵抗降雨或地表水侵蚀的能力愈低，泥石流敏感度愈高。

（2）X2该值表示整个泥石流流域内山坡的平均坡度，较大的坡度值表示坡体稳定性较差，因此流域内山坡坡度大小是泥石流发生的重要因素之一[19]。

（3）X3主沟平均比降表征泥石流主沟的平均坡度，该值愈大，表征泥石流侵蚀能量愈高和流速愈大。

（4）X4流域面积愈大，汇水能力及产生松散物源的能力愈大。

（5）X5形状因子可以由公式 F = A/L20确定，其中A为流域面积，L0为主沟长度。当F值大于1时，通常流域呈狭长和主沟两侧坡度呈陡峻的特点，这就容易造成崩塌发生和松散物源堆积在主沟床，因此，形状因子是泥石流敏感性分析的一个重要影响因子[19]。

（6）X6主沟长度表征泥石流流程大小和沿途接受松散物源补给的能力。文中77%的泥石流沟主沟长度在5～20 km的范围内。

（7）X7主沟床弯曲系数可反映泥石流的排放状况。主沟床弯曲系数愈大，表面在水流的侵蚀作用下主沟床两侧的岩土体稳定性愈差。被侵蚀而崩塌的岩土体将不可避免地成为泥石流物源。

（8）X8沟壑密度综合反映流域内地质构造、地层岩性和岩体的风化程度，因为沟壑总是发育在流域内结构脆弱处[11]。

（9）X9植被可影响坡体的结构、物质组成、岩土体风化程度和强度、含水率等物理力学性能，直接决定坡体的稳定性，进而可影响松散固体物质的储量。一些学者已经证实植被覆盖情况对坡体的稳定性具有重要意义[22]。

根据前人研究，本文将泥石流敏感性分为4个等级，则评价空间 U ={C1,C2,C3,C4}，分别代表A、B、C和D 4个等级，即轻度、中度、重度和极度敏感性，各因子的分级标准如表2所示[11,17－19]。

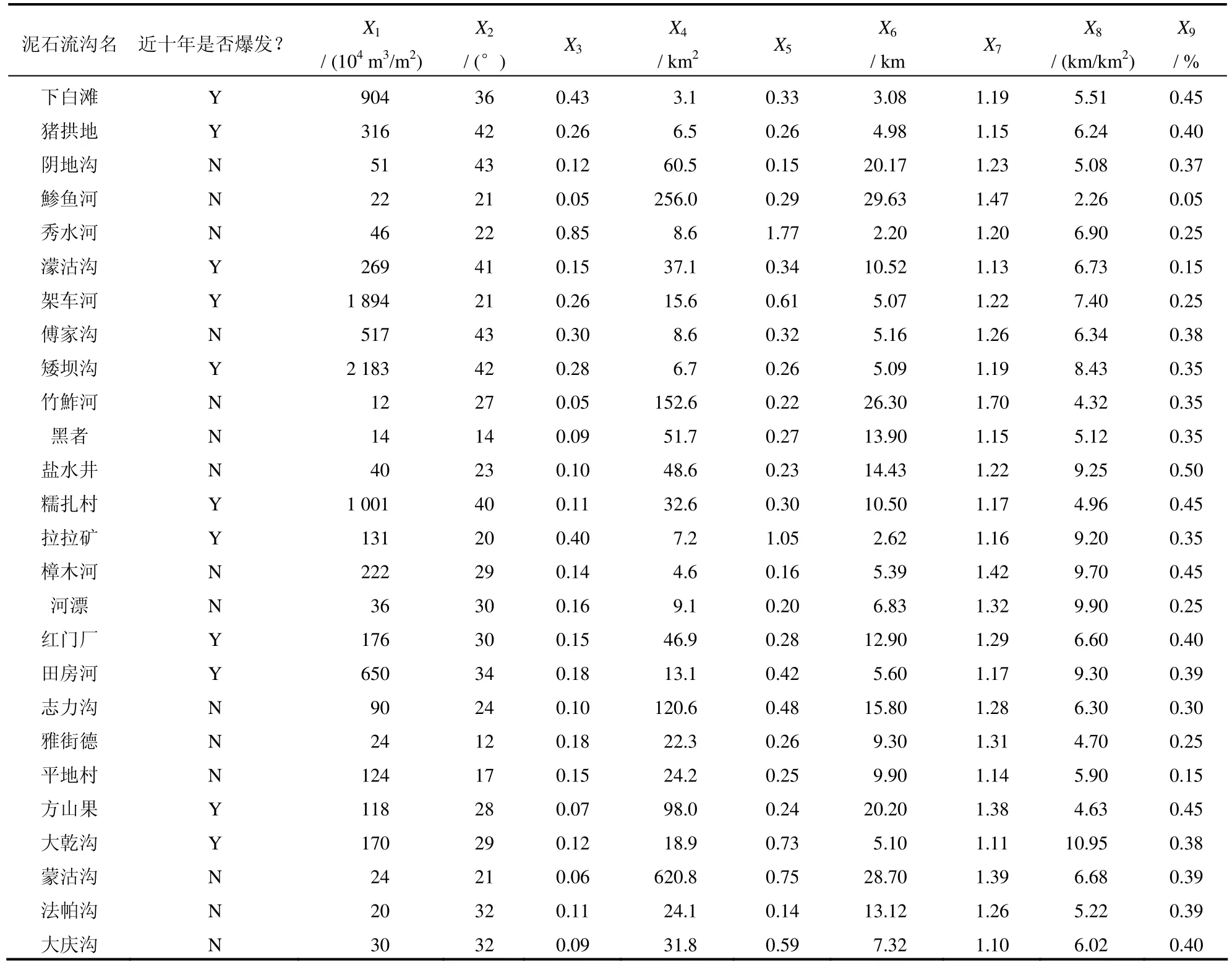
表1 各影响因子指标值Table 1 Values of each major factor

表2 敏感性分级标准Table 2 Boundaries for susceptibility classes

5.2 构建单指标测度评价矩阵

根据泥石流敏感性分级标准，从严考虑，A级指标特征值给出的区间下限值作为A级标准；D级特征值以区间上限值作为D级标准；B、C级特征值则取区间中值作为分级标准。根据上述原则，分别绘制各单项指标的测度函数（图1和图2分别以因子X1和X2为例）。

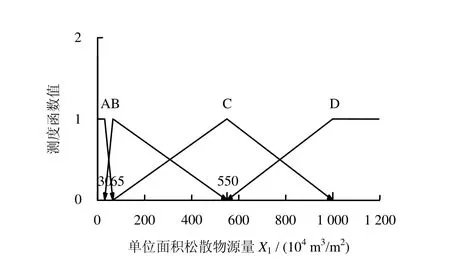
图1 单位面积松散物源量单指标测度函数Fig.1 Unascertained measurement function of loose material volume per square kilometer

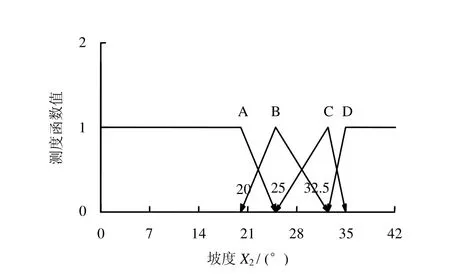
图2 坡度单指标测度函数Fig.2 Unascertained measurement function of slope

查阅表1中的泥石流沟评价指标值，以下白滩泥石流沟单位面积物源量为例，9.04×106m3属于C、D等级（更趋近于D），则 A、B级为 0；将9.04×106m3代入绘制的测度函数中，便可求出属于C、D等级的测度值分别为0.2133、0.7867。同理，可求出其余各因子指标值隶属于某等级的测度值，最终可得下白滩泥石流沟的单指标测度矩阵：

5.3 因子权重的确定

根据现场可知，有15条泥石流沟近十年爆发次数为0，标记为“N”，其余各泥石流沟近十年爆发次数至少为1次，标记为“Y”，如表1第1列所示。根据第 2节介绍的最小熵分析理论，基于Fortran语言自编程序，以近十年每条沟是否爆发泥石流为结果条件，将因子指标值进行随机组合，建立了8192个子模型，并求得了每个子模型的最小熵值，部分子模型的熵值计算结果见表 3。如果某个指标的最小熵值越小，说明该指标值得变异程度就越大，提供的信息量就越多，在综合评价中该指标所起作用和子模型中出现的频率就越大，权重值也就越大；反之，某个指标的最小熵值越大，表明该指标值变异程度小，对系统提供的信息少，在综合评价中该指标所起作用和子模型中出现的频率就越小，权重值也就越小。

通过对每个子模型的最小熵计算可以发现，在所有子模型中，最小熵取值区间在2.4237和3.6585之间，最大差值 K1为1.1448。第16个子模型与第15个子模型之间最小熵值的差值 K2=0.1273，K2/K1=11.12%＞10%。因此，当假定最小熵的分辨率水平为10%时[16]，前15个子模型就可以与其他子模型区别开。因此，可以说这15个子模型是最有效的，最能解释现在所研究的泥石流系统。然而需要指出的是，由于数据测量精度的问题，无法进一步区分这15个子模型的优劣。

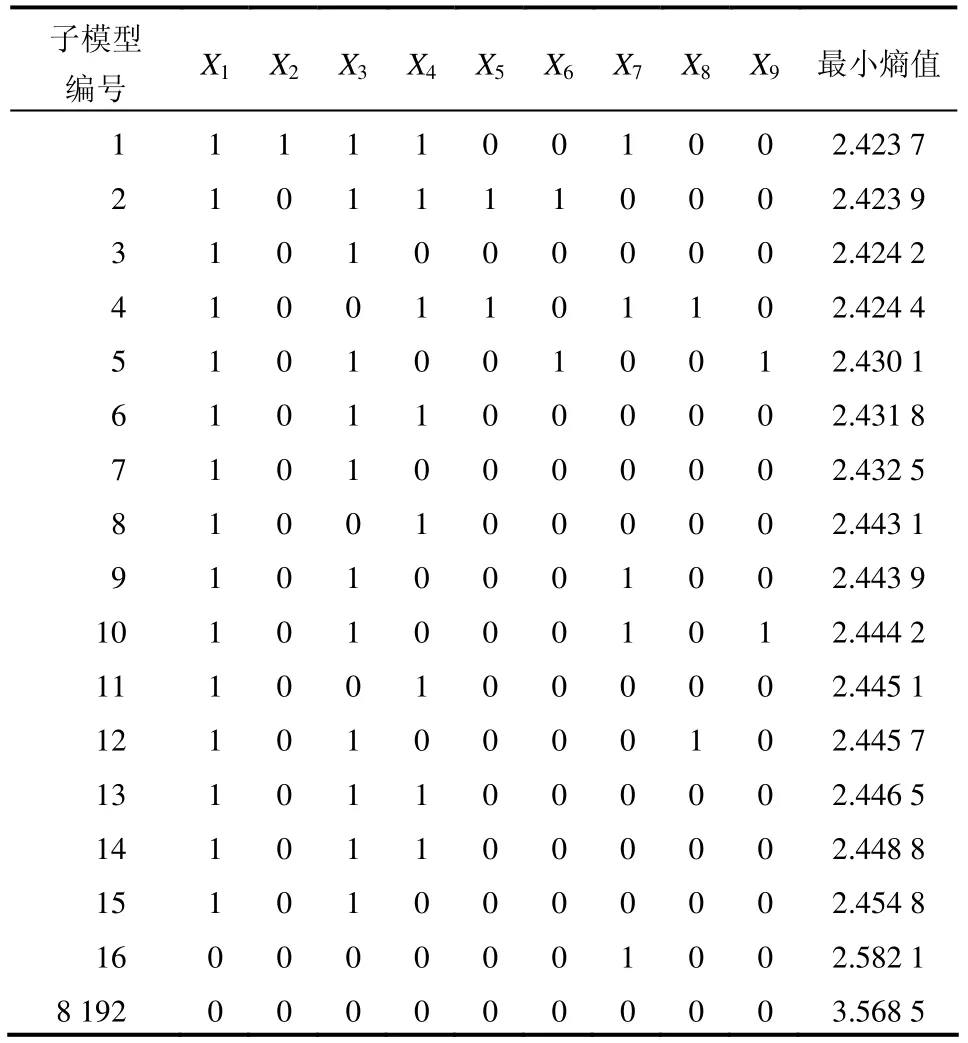
表3 子模型及最小熵值计算结果Table 3 Submodels and their entropy values

在15个有效子模型中，因子X1～X9出现的频率分别为15、1、12、8、1、2、3、2和2。不难发现单位面积物源量、主沟床平均比降和流域面积出现的频率最大，说明其对泥石流系统的贡献率较大，为泥石流敏感性分析的主要影响因子。由表1中数据也可发现，单位面积物源量、主沟床平均比降和流域面积的实测值变异程度较大，因此，其对系统提供的信息和出现的频率是最大的。将各因子在有效子模型中出现的频率归一化即可得其对应的权重值，即因子X1～X9的权重值分别为0.3261、0.0217、0.2609、0.1739、0.0217、0.0435、0.0652、0.0435和0.0435。

5.4 构建多指标测度评价矩阵

以上已经求得单指标测度矩阵和各指标的相对权重值，然后根据式（5），便可求得泥石流沟的多指标测度评价矩阵。下白滩泥石流沟的多指标测度评价矩阵为{0.1133，0.2055，0.0798，0.6014}。同理，可求得其他泥石流沟的多指标测度评价矩阵。

5.5 置信度判别

在泥石流敏感度分析过程中，假设评价结果A比B好，B比C好，C比D好，评价等级顺序依次为A、B、C、D，因此，可以采用置信度识别准则对泥石流进行危险度评价。以下白滩泥石流为例，取置信度λ=0.5，根据多指标测度评价矩阵和式（7），按照从小到大顺序，0.1133+0.2055+0.0798=0.3986＜λ=0.5，因此 k0=4，即下白滩泥石流敏感性等级为D；由大到小，0.6014+0.0798=0.6812＞λ=0.5，即下白滩属于D级。可见，两次判别结果一致，因此，可以判定下白滩泥石流敏感性等级为D级，属极度敏感性。λ取值为 0.5，所有泥石流沟都满足置信度准则。若取λ=0.6，盐水井由小到大的分析结果为中度，由大到小的的分析结果为轻度，这显然是不合理的，不符合置信度准则；同样，若取λ=0.7，分析结果亦不满足置信度准则。类似与盐水井沟情况的还有拉拉矿、红门厂和法帕沟，因此本文中取λ=0.5是合理的。同理，应用上述方法取λ=0.5对其余25条泥石流沟进行敏感度分析，分析结果如表4和图3所示。

5.6 结果分析及防治建议

文献[11]研究区和对象与本文相同，其采用层次分析法和熵值法分别确定因子的主观和客观权重，然后基于组合赋权确定了因子的最终权重，故所得权重值既能反映研究者对研究对象的主观认知，又能包含因子取值所代表的客观信息，权重更加合理可靠，最终敏感性分析结果由可拓学理论确定，结果可靠性较高；同时，本文又利用权的最小平方法[23]求得了 X1～X9的权重值分别为 0.3242、0.0230、0.1948、0.2443、0.0313、0.0432、0.0639、0.0347和0.0406，该权重为主观权重，充分反映了研究者对研究区现场情况的认知；最后，同样基于未确知测度理论分析了各泥石流沟的敏感性，结果罗列于表4最后一列。

由表 4可知，本文分析结果与文献[11]中对泥石流敏感度分析结果基本一致，仅有下白滩、驾车河、盐水井、糯扎村沟、拉拉矿、红门厂和法帕沟分析结果与文献有所差异；与采用主观权重所得的分析结果相比，仅有猪拱地、矮坝沟和盐水井沟有所差异。受长江三峡勘测研究院有限公司（武汉）的委托，吉林大学建设工程学院科研小组于2008年9月28日至11月8日对乌东德库区泥石流进行了为期一个多月的现场调研，调研结果见表 5。由表中结果可知，盐水井和法帕沟流域内极少见崩塌或者滑坡发育，物源较少，因此本文分析其敏感性为轻度合乎情理；拉拉矿和红门厂流域内虽有滑坡或者崩塌发生，但因为其属于中度敏感性的隶属度分别为0.5350和0.5626，远大于属于其他等级的隶属度，所以无论按照隶属度最大准则，还是按照置信度识别准则将其判定为中度显然是可以接受的；下白滩沟、猪拱地、驾车河沟、矮坝沟和糯扎村沟（图 4）物源极为丰富，在降雨和地震作用下崩塌滑坡发育，而且规模较大，流通区通道狭窄，常呈“V”字型，且泥石流发生频率较高，最近十年均有爆发记录，因此本文的敏感度分析结果与现场泥石流发育情况更加吻合。

同时，由表4可知，敏感性分析结果为轻度或者中度的泥石流沟内无或者少有崩塌或者滑坡发育，极大地减少了流域内的物源量；敏感性分析结果为重度或者极度的泥石流沟内龙街粉砂层、马店河堆积层、红层和第四系堆积物广泛分布，在降雨和地震的作用下滑坡或崩塌极易发生，可为泥石流的爆发提供大量物源（见图 5～7）。因此，总的来说，本文泥石流敏感性分析结果与泥石流实际发育情况是一致的。

此外，由表4、5可知，拉拉矿、红门厂、方山果沟和大乾沟的敏感性分析结果为中度，而其他在近十年爆发次数至少为1次的泥石流沟的敏感性分析结果多为重度或极度，因此，从减灾防灾的角度来说，本文的评价结果是偏保守的。

对于轻度敏感性的泥石流沟，流域内不良地质现场发育较少，物源量少，活动性弱，可不对其防护，或者只采取生物工程保持水土；对于中度敏感性的泥石流沟，流域内发育有一定的滑坡和崩塌，故建议根据具体情况采用一种或若干种防治措施综合治理，防止过度的人类改造或采矿活动，以免破坏坡体稳定性，产生大量崩滑物源补给泥石流；对于重度和极度敏感性的泥石流沟，大多靠近坝址区，且流域内崩塌和滑坡发育，物源量巨大（单位面积物源量最大可达22183 × 104m3/km2），建议采用排导工程、渡槽工程和拦砂坝工程等手段重点治理[24]。

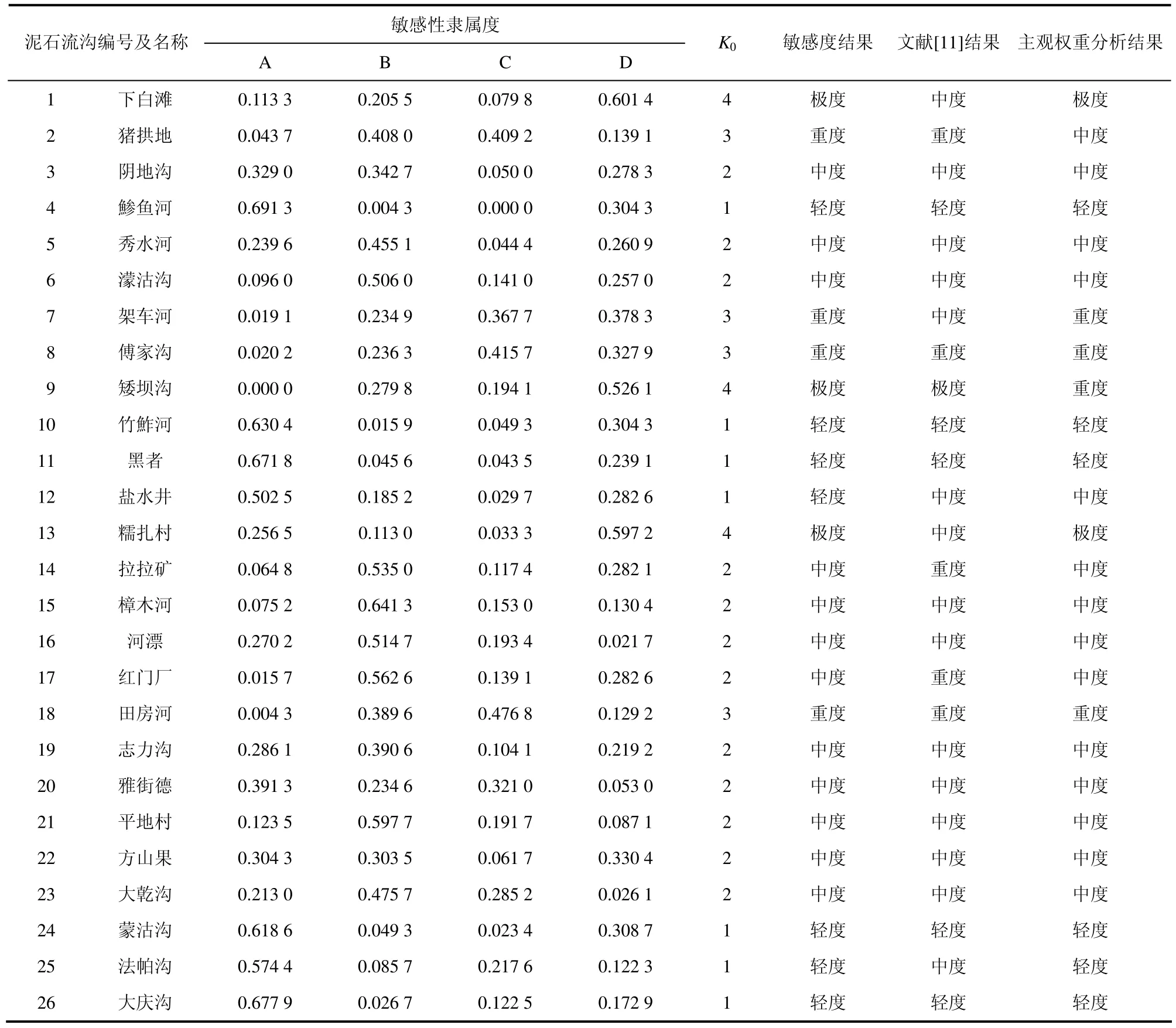
表4 泥石流敏感度分析结果Table 4 Susceptibility analyzing results of debris flow catchments

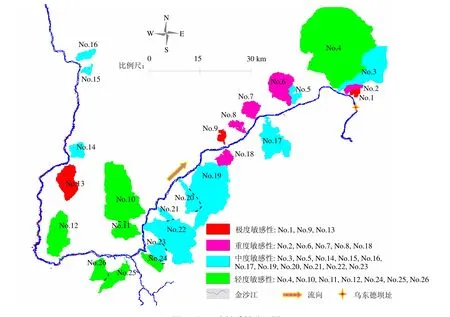
图3 泥石流敏感性分区图Fig.3 Debris flow susceptibility partition map

表5 泥石流沟敏感性分析结果及现场调查情况Table 5 Comparison between predicted debris flow susceptibility and field observations

图4 糯扎村沟沟流通区主沟两滑坡塌现象Fig.4 Collapse in Nuozhacun catchment

图5 矮坝桥沟流通区主沟两滑坡塌现象 Fig.5 Collapse in Aibaqiao catchment

图6 拉拉矿沟流通区主沟两侧崩塌现象Fig.6 Collapse in Lalakuang catchment

图7 拉拉矿沟流通区局部小型泥石流 Fig.7 Local debris flow in Lalakuang catchment

6 结 论

（1）最小熵分析原理是一种基于熵的新的变量选择和数据分析方法，过程简单明了，很容易扩展并应用到含有多个相关或非相关变量的复杂的地球物理或地质资料分析中，既能克服因子分析过程中的人为主观性，又能客观全面地确定各因子对系统的贡献率，优选出主要影响因子，必要时还可对影响因子提出一种量化标准，确定各因子的权重。本文基于最小熵分析原理确定单位面积物源量、主沟床平均比降和流域面积为对泥石流系统贡献率最大的影响因子，与前人研究成果基本一致，因此，将最小熵分析原理应用到泥石流敏感性分析中是可行的。

（2）未确知测度理论源于测度空间，严格地，满足测量准则，相较于其他方法普适性更强。本文基于未确知测度理论建立的泥石流敏感性分析模型，敏感性分析结果与文献[11]结果及基于权的最小平方法的分析结果基本一致。对现场调查资料充分分析后得知，本文敏感性分析结果基本反映了泥石流实际发育情况，仅有4条沟敏感性结果偏于保守。因此，利用本文所提出的模型进行泥石流敏感度分析是十分有效的。虽然从减灾防灾的角度来说，分析结果是偏于保守的，但仍具有一定的实际应用价值。

（3）需要指出的是，虽然最小熵分析程序提供了一种诚实的方式用来从眼花缭乱的数据中提取重要信息，但是最小熵分析的分辨率受数据测量精度和正确性的限制，这意味着测量数据本身的不正确性会导致整个最小熵分析过程是在病态的情况下进行的。因此，在各因子指标收集和分析的过程中保证数据精度是必要的。

[1]CHEN N S,YUE Z Q,CUI P,et al.A rational method for estimating maximum discharge of a landslide-induced debris flow: A case study from Southwestern China[J].Geomorphology,2007,84(1): 44－58.

[2]GLADE T.Linking debris-flow hazard assessments with geomorphology[J].Geomorphology,2005,66(1): 189－213.

[3]LIU X L,LEI J Z.A method for assessing regional debris flow risk: An application in Zhaotong of Yunnan province(SW China)[J].Geomorphology,2003,52(3): 181－191.

[4]铁永波,唐川.层次分析法在单沟泥石流危险度评价中的应用[J].中国地质灾害及防治学报,2006,17(4):79－84.TIE Yong-bo,TANG Chuan.Application of AHP in single debris flow risk assessment[J].The Chinese Journal of Geological Hazard and Control,2006,17(4): 79－84.

[5]LIN P S,LIN J Y,LIN S Y,et al.Hazard assessment of debris flows by statistical analysis and GIS in Central Taiwan: Multivariate statistical analysis[J].International Journal of Applied Science and Engineering,2006,4(2): 165－187.

[6]SHEN C W,LO W C,CHEN C Y.Evaluating susceptibility of debris flow hazard using multivariate statistical analysis in Hualien County[J].Disaster Advances,2012,5(4): 743－755.

[7]LIU Y,GUO H C,ZOU R,et al.Neural network modeling for regional hazard assessment of debris flow in Lake Qionghai Watershed,China[J].Environmental Geology,2006,49(7): 968－976.

[8]CHANG T C.Risk degree of debris flow applying neural networks[J].Natural Hazards,2007,42(1): 209－224.

[9]CHANG T C,CHIEN Y H.The application of genetic algorithm in debris flows prediction[J].Environmental Geology,2007,53(2): 339－347.

[10]孟凡奇,李广杰,秦胜伍,等.基于证据权法的泥石流危险度区划[J].吉林大学学报(地球科学版),2010,4(6):1380－1384.MENG Fan-qi,LI Guang-jie,QIN Sheng-wu,et al.Zoning of debris flow hazard degree with weightof-evidence method[J].Journal of Jilin University(Earth Science Edition),2010,4(6): 1380－1384.

[11]ZHANG W,CHEN J P,WANG Q,et al.Susceptibility analysis of large-scale debris flows based on combination weighting and extension methods[J].Natural Hazards,2013,66(2): 1073－1100.

[12]王光远.未确知性信息及其数学处理[J].哈尔滨建筑工程学院学报,1990,23(41): 52.WANG Guang-yuan.Unascertamed Information and its mathematical treatment[J].Journal of Harbin University of Architecture and Engineering,1990,23(4): 52.

[13]刘开第,吴和琴,庞彦军,等.不确定性信息数学处理及应用[M].北京: 科学出版社,1999.

[14]宫凤强,李夕兵,董陇军,等.基于未确知测度理论的采空区危险性评价研究[J].岩石力学与工程学报,2008,27(2): 321－330.GONG Feng-qiang,LI Xi-bing,DONG Long-jun,et al.Underground goaf risk evaluation based on uncertainty measurement theory[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(2): 321－330.

[15]唐海,万文,刘金海.基于未确知测度理论的地下洞室岩体质量评价[J].岩土力学,2011,38(4): 1181－1185.TANG Hai,WAN Wen,LIU Jin-hai.Evaluation of underground cavern rock quality based on uncertainty measure theory[J].Rock and Soil Mechanics,2011,38(4): 1181－1185.

[16]CHEN C C,TSENG C Y,DONG J J.New entropy based method for variables selection and its application to the debris-flow hazard assessment[J].Engineering Geology,2007,94(1): 19－26.

[17]匡乐红,徐林荣,刘宝琛.基于可拓方法的泥石流危险性评价[J].中国铁道学,2006,27(5): 1－6.KUANG Le-hong,XU Lin-rong,LIU Bao-chen.Debris flow hazard assessment based on extension method[J].China Railway Science,2006,27(5): 1－6.

[18]LIN P S,LIN J Y,HUANG J C,et al.Assessing debrisflow hazard in a watershed in Taiwan[J].Engineering Geology,2002,66(3): 295－313.

[19]CHANG T C,WANG Z Y,CHIEN Y H.Hazard assessment model for debris flow prediction[J].Environmental Earth Sciences,2010,60(8): 1619－1630.

[20]陈鹏宇,于宏明,刘勇,等.基于独立信息数据波动赋权的泥石流危险度评价[J].岩土力学,2013,34(2):449－454.CHEN Peng-yu,YU Hong-ming,LIU Yong,et al.Evaluation of debris risk based on independent information data fluctuation weighting method[J].Rock and Soil Mechanics,2013,34(2): 449－454.

[21]陈鹏宇,乔景顺,彭祖武,等.基于等级相关的泥石流危险因子筛选和危险度评价[J].岩土力学,2013,34(5):1409－1415.CHEN Peng-yu,QIAO Jing-shun,PENG Zu-wu,et al.Screening of debris flow risk factors and evaluation based on rank correlation[J].Rock and Soil Mechanics,2013,34(5): 1409－1415.

[22]ERCANOGLU M,GOKCEOGLU C.Use of fuzzy relations to produce landslide susceptibility map of a landslide-prone area(West Black Sea region,Turkey)[J].Engineering Geology,2004,75(3): 229－250.

[23]CHU A T W,KALABA R E,SPINGARN K.A comparison of two methods for determining the weights of belonging to fuzzy sets[J].Journal of Optimization Theory and Applications,1979,27(4): 531－538.

[24]周必凡,李德基,罗德富.泥石流防治指南[M].北京:科学出版社,1991.