灰色关联分析法在电子设备故障树中的应用

赵红言， 张 君， 张建强

(空军工程大学理学院，陕西西安 710051)

0 引言

灰色系统理论［1-3］是一种综合运用数学分析方法，对含有未知信息的系统利用已知信息通过信息处理进行预测、判断与决策的理论。灰色关联分析是灰色系统理论中的关键内容之一，它指的是事物之间的不确定关联。灰色关联分析能够通过数据对系统不同状态进行比较，从而识别系统故障。在电子设备中，故障原因与故障征兆之间并不是一一对应的关系，因此可将电子设备看作是一个复杂的灰色系统，把灰色理论的概念和方法引入到电子设备故障诊断领域，利用已知的故障模式去判别设备的状态，从而进行设备的故障诊断［4］。

故障树分析法(FTA)［5-6］是一种图形化的系统可靠性、安全性以及故障诊断的分析方法。FTA首先选定某一影响最大的系统故障作为顶事件，然后将造成系统故障的原因逐级分解为中间事件，直到把不能或不需要分解的基本事件作为底事件为止，体现了故障传播的层次性和子、父节点之间的因果关系［7］。利用FTA可以形象、直观表述自动化系统是怎样失效的，从而找出系统的薄弱环节，以便改进设计，改进使用和维修方案，并能分析其安全性。本文运用灰色关联理论对复杂电子设备系统FTA中造成顶事件的各种故障模式进行分析，为电子设备的设计和维修提供了理论依据，也为提高系统的可靠性提供了参考［8］。

1 灰色关联模型的建立

1.1 构造标准故障模式向量

在故障树分析中，导致故障树顶事件发生的底事件可能有许多不同的组合，每一种组合称为一个割集。而最小割集是导致故障树顶事件发生的最少数量底事件的集合，最小割集发生时，顶事件必然发生［9］。全部最小割集的完整集合代表了顶事件发生的所有可能性，这些可能性即代表引起故障树顶事件发生的一种故障模式。

设T为顶事件，最小割集(即故障原因向量)个数为m，底事件数为n，其结构函数可表示为

用Ki(i=1，2，…，m)表示最小割集，Xj(j=1，2，…，n)表示底事件，可以看出，第i个最小割集Ki由n个底事件x1，x2，…，xn组合而成。在最小割k中，令ni个底事件全为“1”，其余(n－ni)个底事件为“0”，这样m个最小割集就构成了一个典型的标准故障模式矩阵:

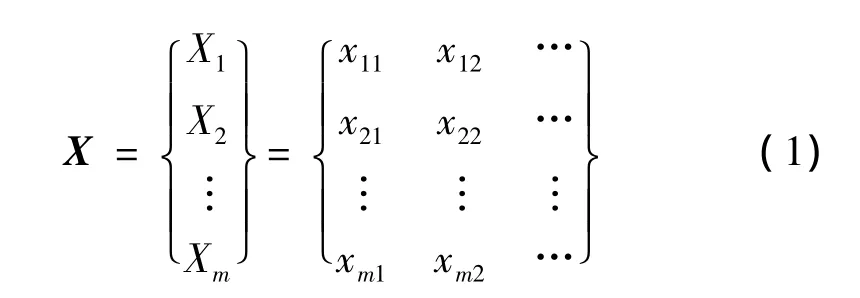
式中，xij表示第i类故障模式下第j个基本事件数据。

1.2 确定待检故障模式向量

为了求得导致故障树顶事件发生的各种故障模式(即m个最小割集)发生的可能性，可以从底事件的重要度入手来加以分析。不同的底事件对于顶事件发生与否的影响程度是不一样的，即其重要度不尽相同。其中关键重要度不仅体现了底事件在故障树中的地位，而且还体现了事件本身的不可靠度，所以它更能客观地体现部件对系统故障树的影响［10］。

基本事件的关键重要度由下式计算:

式中:Ig为基本事件的概率重要度系数;P(T)为顶事件的发生概率;qj为第j个基本事件的发生概率。

这样，n个底事件按其关键重要度组成一组待检模式向量，作为比较向量:

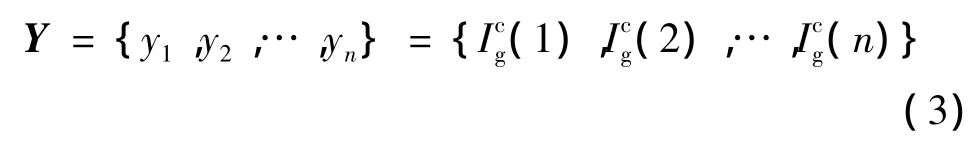
2 关联系数及关联度的计算

2.1 数据的无量纲化处理

为了便于分析和比较，在进行灰色关联分析前，必须先对原始数据进行无量纲化处理。比较常用的无量纲化处理方法有区间化方法、最大值化方法以及均值化方法［11］。其中最大值化方法的计算公式为

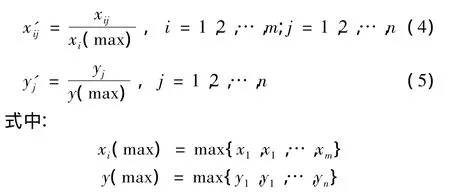
2.2 关联系数计算

待检模式向量Y与标准模式向量X在k点的关联系数表达式为

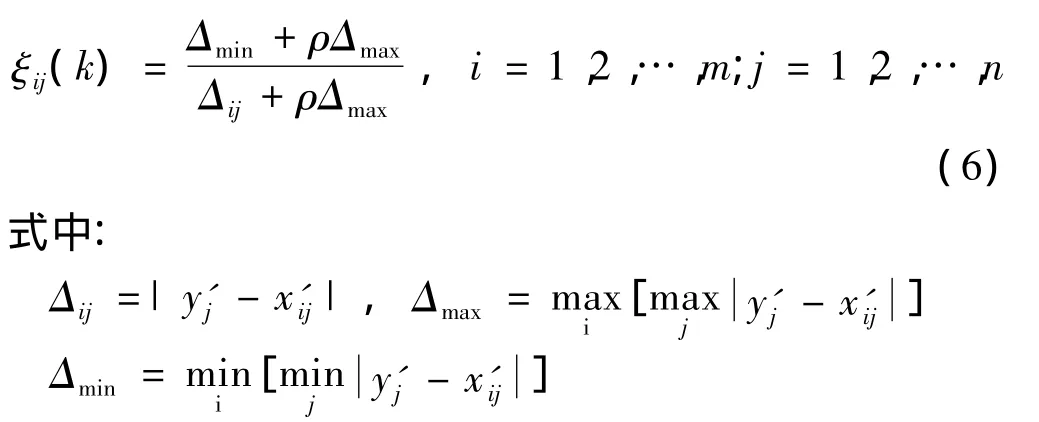
ρ为分辨系数，通常在0与1之间取值。它的作用是为削弱最大绝对差数值太大而失真的影响，提高关联系数之间的差异显著性，所以ρ的取值影响关联度的大小与排列顺序［12-13］。当 ρ≤0.546 3时，分辨力最好［14］，本文选取 ρ=0.5。

2.3 关联度系数计算

灰色关联度［15］是表征2个灰色系统之间相似性的一种指标，为［0，1］区间内变化的量，且关联度越接近1，该子序列对母序列的影响越敏感;反之，关联度越接近0，其影响越不敏感［16］。关联度的计算可采用平均值法:

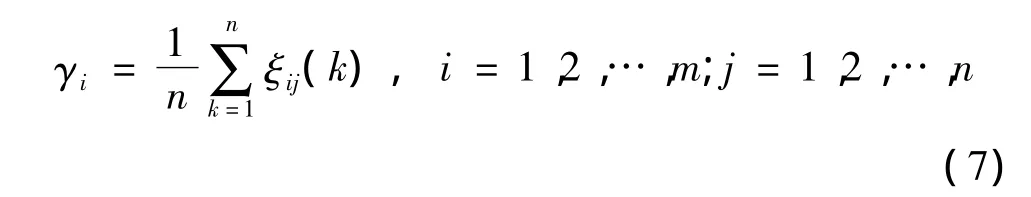
式中:ξij(k)为Y与第i个标准向量在k点的关联系数。

2.4 根据关联度大小进行排序

根据式(7)可得到关联度序列R=［γ1，γ2，…，γm］，按照从大到小的顺序对所有关联度进行排列，以此判断待检故障模式与各标准故障模式的接近程度，选择最大关联度对应的标准故障模式作为诊断的输出结果，从而实现系统故障状态的识别。

3 实例分析

以某数控系统电源故障为例建立故障树，如图1所示。图中:顶事件T为电源故障;M1为指示灯亮;M2为报警灯亮;M3为正常仍无通电;M4为电源模块报警;M5为外部报警;M6为信号不良;M7为单元电源切断。

图1 电源系统故障树

3.1 求解最小割集

采用下行法求解最小割集［17］，求出的最小割集为:X1={x1}，X2={x2}，X3={x3}，X4={x4}，X5={x5}，X6={x6}，X7={x7}，X8={x8}，X9={x9}，X10={x10}，X11={x11}，X12={x12}，共有12 个最小割集，即m=12。

3.2 求特征矩阵

底事件为12个，即n=12，最小割集中所包含的底事件在特征矩阵中取为1，其余为0，则特征矩阵为

3.3 求待检模式向量

根据各底事件在故障树中的发生的概率，可以得到各底事件的关键重要度，如表1所示。由其组成的待检模式向量为

表1 关键重要度

3.4 计算关联系数

由于标准模式向量无量纲，所以只对待检模式向量数据进行无量纲化处理:

然后，以Y'(j)为参考序列，计算其与标准模式向量X的绝对差值:

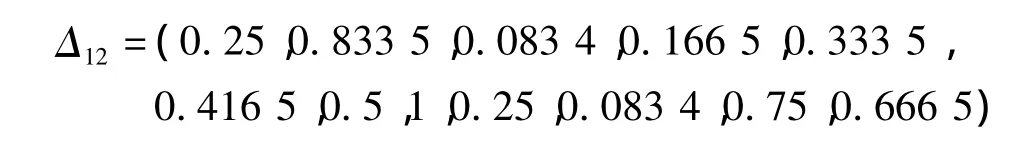
以此结果计算关联系数，如表2所示。

表2 关联系数表

3.5 计算关联度

由 γi=)计算关联度，结果如下:γ1=0.538，γ2=0.591，γ3=0.517，γ4=0.529，γ5=0.546，γ6=0.554，γ7=0.561，γ8=0.616，γ9=0.538，γ10=0.517，γ11=0.583，γ12=0.546。

将关联度由大到小排列，得到γ8＞γ2＞γ11＞γ7＞γ6＞γ5=γ12＞γ1=γ9＞γ4＞γ3=γ10。由此可以得到造成电源故障的12种模式中最小割集x8对电源失效的影响最大，其次分别为x2、x11、x7等。该结论与表1中底事件关键重要度大小的排序是一致的。但表1中的数据只是单纯地从重要度的角度来判断各底事件发生故障可能性的大小，没有体现出系统的故障特征与内部特征之间的相关性。而对系统进行定量分析后得出，能更加直观地反映出系统中各底事件故障发生的可能性大小。

4 结语

在电子设备故障树分析中，通过构造标准模式矩阵和待检模式向量，运用灰色关联分析技术，对最小割集组成的各种故障模式按关联度大小进行排序，从而找出导致系统故障发生的主要因子。该方法计算便捷、易于实现、结果可靠，能够为电子设备维修及状态预测提供理论指导，具有可行性。文中对某数控系统的电源系统故障进行了计算，结果表明该方法有效，结论客观。

［1］邓聚龙.灰理论基础［M］.武汉:华中科技大学出版社，2002:1-7.

［2］刘思峰，党耀国，方志耕，等.灰色系统理论及其应用(第5版)［M］.北京:科学出版社，2010:1-6.

［3］陈永光，柯宏发.电子信息装备试验灰色系统理论运用技术［M］.北京:国防工业出版社，2008:18-25.

［4］李政仪.基于灰色关联的容差模拟电路故障诊断［J］.科学技术与工程，2008，8(15):4402-4405.

LI Zheng-yi.Fault diagnosis of analog circuits with tolerance based on gray correlation degree［J］.Science Technology and Engineering，2008，8(15):4402-4405.

［5］沈庆根，郑水英.设备故障诊断［M］.北京:化学工业出版社，2009:19-20.

［6］金 星，洪延姬.系统可靠性与可行性分析方法［M］.北京:国防工业出版社，2007:3-12.

［7］迟 媛，钱 巍，金英子.基于故障树理论的不精确推理方法研究［J］.东北农业大学学报，2006，37(2):206-210.

CHI Yuan，QIAN Wei，JIN Ying-zi.Study on not precise reasoning method based on fault tree theory［J］.Science Technology and Engineering，2006，37(2):206-210.

［8］张凤鸣，惠晓滨.航空装备故障诊断学［M］.北京:国防工业出版社，2010:25-40.

［9］朱大奇，于盛林.基于故障树最小割集的故障诊断方法研究［J］.数据采集与处理，2002，17(3):341-344.

ZHU Da-qi，YU Sheng-lin.Diagnosis approach based on minimal cut sets of fault trees［J］.Journal of Data Acquisition ＆ Processing，2002，17(3):341-344.

［10］赵静一，王 颖，李 侃.高炉炉顶液压系统的设计及故障树分析［J］.冶金设备，2006，156(2):58-61.

ZHAO Jing-yi，WANG Ying，LI Kan.Design and fault tree analysis of hydraulicsystem for blastfurnace arch［J］. Metallurgical Equipment，2002，17(3):341-344.

［11］黎奇志，胡国平，赵红言.加权灰色关联分析在故障诊断中的应用研究［J］.微计算机信息，2012，28(7):28-30.

LI Qi-zhi，HU Guo-ping，ZHAO Hong-yan. Research on then application of weighted grey relational analysis in fault diagnosis［J］.Microcomputer Information，2012，28(7):28-30.

［12］东亚斌，段志善.灰色关联度分辨系数的一种新的确定方法［J］.西安建筑科技大学学报(自然科学版)，2008，40(4):589-592.

DONG Ya-bin，DUAN Zhi-shan.A New determination method for identification coefficient of grey relational grade［J］.J Xi’an Univ of Arch ＆ Tech(Natural Science Edition)，2008，40(4):589-592.

［13］孙才新，李 俭，郑海平，等.基于灰色面积关联度分析的电力变压器绝缘故障诊断方法［J］.电网技术，2002，26(7):25-29.

SUN Cai-xin，Li Jian，ZHENG Hai-ping，et al.New method of faulty insulation diagnosis in power transformer based on degree of area incidence analysis［J］.Power System Technology，2002，26(7):25-29.

［14］刘淑娟.基于灰色关联度分析算法的教学评价系统设计［J］.科技通报，2012，28(6):65-66.

LIU Shu-juan.Teaching evaluation system design based on the improved algorithm of grey relational analysis［J］.Bulletin of Science and Technology，2012，28(6):65-66.

［15］邓聚龙.灰色系统基本方法［M］.2版.武汉:华中科技大学出版社，2005，1-21.

［16］李瑰贤，于广滨，孙 瑜.基于灰色关联的微小型活齿传动模糊故障树分析［J］.中国工程机械学报，2006，4(2):127-132.

LI Gui-xian，YU Guang-bin，SUN Yu.Application of grey-relational theory in fault tree analysis of miniature sine oscillating tooth gear drive［J］.Chinese Journal of Construction Machinery，2006，4(2):127-132.

［17］李卫宁，高洪林，马 亮.潜艇鱼雷应急发控系统故障树最小割集的求解［J］.四川兵工学报，2010，31(8):43-46.

LI Wei-ning，GAO Hong-lin，MA Liang.The minimal cut sets solving of fault trees of emergency control system in submarine torpedo［J］.Sichuan Ordnance Journal，2010，31(8):43-46.