奇异系统重置观测器的稳定性分析
2014-05-17张小茜吴保卫李保平
张小茜,吴保卫,李保平
(陕西师范大学数学与信息科学学院,西安 710062)
奇异系统重置观测器的稳定性分析
张小茜,吴保卫,李保平
(陕西师范大学数学与信息科学学院,西安 710062)
研究了奇异系统重置观测器的稳定性问题.通过构造李雅普诺夫函数,结合线性矩阵不等式和S-Procedure方法,给出了奇异系统重置观测器二次稳定和输入输出稳定的充分条件.最后数值算例表明了结论的有效性.
奇异系统;重置观测器;二次稳定性;线性矩阵不等式
0 引言
状态观测器是一种递归算法,它在很多应用领域中起着十分重要的作用,比如故障的检测以及监控、容错控制等等.状态观测器分为比例、比例积分等几种类型,本文主要研究自适应状态观测器.从20世纪70年代起,很多学者就开始了对自适应观测器的研究.起初研究的是比例观测器,它的特点是在自适应率里只有一个输出观测误差的比例中项,文献[1-2]分别研究了线性时不变系统和非线性系统的比例观测器.为了能够提高比例观测器的鲁棒性,在自适应率中添加一项积分项,这样合成的观测器就被称为比例积分观测器.文献[3-4]表明比例积分观测器在线性时不变系统和非线性系统中较比例观测器有更好的应用效果.但是,由于自适应率都是线性的,因而无法降低预测过程中出现的过冲量和设定上升时间情况下求预测过程时间所需的计算量.为了解决这个问题,一种有效方案是在自适应率中添加重置因子.重置因子的简化形式就是由积分和重置率构成,其中重置率指的是只要满足重置条件就重置积分的输出项.重置因子是由Clegg于1958年首次提出,他将其定义为当输入为零时就将输出重置为零的一种积分;[5]1974年,Horowitz给出了这种积分一个更为广义的结构,并称为一阶重置因子.[6]20多年后才出现了关于重置因子稳定性的证明.文献[7]利用了Hβ条件来证明重置系统的稳定性.与文献[8]中所定义的当输入为零时发生重置行为不同,文献[9]则对重置系统进行了更为一般的分析,提出了一种新的重置条件,即当系统的输入输出异号时则重置.
近年来关于重置因子的研究仍然是一个开放的挑战性课题,目前主要的研究集中在控制问题.文献[10]是在状态观测器的框架下讨论重置因子问题,给出了新型观测器——重置观测器.文献[11]则是对文献[10]的一个推广,即考虑最优重置观测器问题.
比起一般的线性系统,奇异系统具有更为一般性的结论和更为广泛的应用.因此奇异系统的研究属于一个热点课题,也取得了大量的研究成果,如文献[12].
受以上文献启发,本文研究了奇异系统的重置观测器问题,提出了奇异重置观测器的概念,其中关于奇异重置观测器所使用的重置条件与文献[9]所提到的方法一致,并给出判断稳定性的充分条件.
1 问题描述及准备
文章采用以下记号:R(C)表示实数(复数)集;Rn表示n维实数向量的集合;Rn×n,Rn×1,R1×n分别表示n×n,n×1,1×n维实矩阵空间;(·)T表示转置;P>0表示矩阵P是对称正定的;I代表单位矩阵; sup代表上确界.
考虑如下形式的单输入单输出(SISO)线性时不变奇异系统Σs:

其中:x∈Rn是状态变量;u∈R是输入变量;ω∈Rn是干扰输入变量;y∈R是输出变量;A∈Rn×n,B∈Rn×1,Bω∈Rn×1和C∈R1×n是已知常量矩阵.
建立如下形式的奇异系统重置观测器:


定义1[13]如果存在s∈C使成立,那么称系统Σξ是正则的.
在保证解的存在唯一性后,接下来讨论重置条件.这个重置奇异观测器也可以看成含有流集F和重置集合,即跳集J的混合系统.在(3)中的两类条件就分别代表流集F和跳集J的条件.当(y~,ξ)∈F时, (3)是一个正常的比例积分观测器;当(y~,ξ)∈J时,通过重置集合Ar=0,积分项就发生重置.
当y~·ξ≥0时,即若y~和ξ同号,则观测器轨迹就是连续平滑的;当y~·ξ<0时,也就是y~和ξ异号,那么观测器轨迹就出现了间断点.易知,集F和集J可等价地用如下方式描述

2 二次稳定性分析

其中:

注1 奇异系统重置观测器(2)-(3)要满足以下两个条件:
(1)η∈J⇒ARη∈F,这个假设是为了保证在每次重置后,所得的解都会映射到流集F上,这样能避免出现一段时间连续重置的情形;
(2)重置时间ti+1-ti≥ρ>0.
上述条件是通过时间正则化来避免奇异系统重置观测器出现奇诺现象.这样做的好处是对于在任意相邻两次重置之间所构成的时间区间长度都超过ρ,其中ρ>0称为驻留时间.
下面利用线性矩阵不等式,给出奇异系统的奇异重置观测器二次稳定的充分条件.
定理1 考虑误差动态系统Ση,Bω=0,如果存在一个矩阵P>0,满足
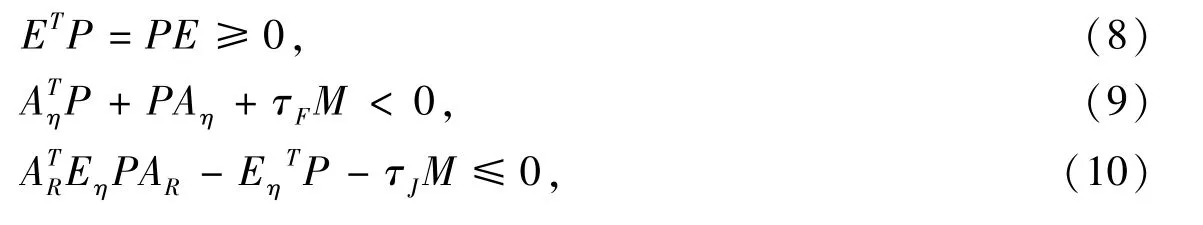
那么Σ
η就是二次稳定的.其中标量子F≥0,子J≥0.证明 对于扩张误差动态系统(7),构造二次李雅普诺夫函数

要证明奇异系统重置观测器是二次稳定的,就需要证明

通过(4),得F:={η:ηTMη≥0}.利用文献[14]中提到的S-Procedure,不等式(12)的第一项就等价于存在子F≥0,满足

对于(11)求导可以得到

由(13)和(14)就得到了(12)的第一项成立的充分条件,即

将(15)转化为P>0和子F≥0条件下的线性矩阵不等式问题,也就是

所得到的结果形式与(9)一致,因此证明了(12)的第一个不等式.
类似的,再次利用S-Procedure方法,(12)的第二个式子成立的充分条件是存在子J≥0满足
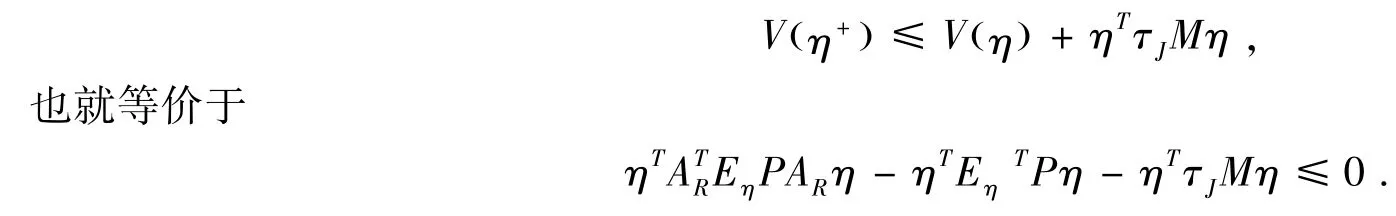
对该式整理后可以写成如下的线性矩阵不等式

这就证明了(12)式中的第二个不等式.
3 输入输出稳定性分析
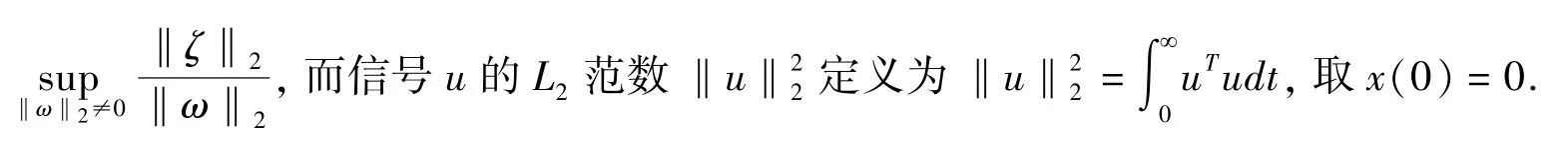
接下来给出奇异系统重置观测器关于输入输出性质的相关结果.定义系统(7)的标准差增益为L2=
下面给出一个引理,在后续的相关定理证明中将会用到.
引理1 假设找到一个二次李雅普诺夫函数V(x)=xTETPx,若存在一个矩阵P>0,满足ETP=PE≥0,并且存在γ>0,使得

那么输入信号为ω和输出信号为ζ构成的奇异系统的L2增益小于γ.

定理2 考虑由Aη,Bη,Cη和AR构成的扩张误差动态系统(7),如果存在一个矩阵P>0,满足ETP= PE≥0,使得

成立.那么系统(7)是输入输出稳定的,并且存在γ>0,使得L2增益小于γ,其中子J≥0,子F≥0.
证明 要证明这个奇异系统重置观测器的输入输出稳定性和奇异系统的L2增益小于γ,就需要证明
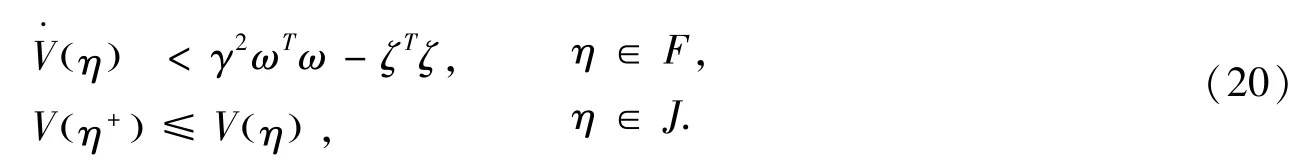
其中:(20)的第一个式子证明依赖于引理1,而第二个式子就等价于(12)中已经证明的第二个式子.因此只需要证明(20)的第一个式子即可.同样的,已经知道F:={η:ηTMη≥0},并且通过运用S-procedure方法,(20)的第一个式子就等价于存在子F≥0,满足

就证明了(20)的第一个式子.定理得证.
4 数值算例

由定理1知系统Ση是二次稳定的.
5 结语
本文研究了奇异系统重置观测器的稳定性问题.构造李雅普诺夫函数,利用线性矩阵不等式和S-Pro-cedure方法,给出了奇异系统重置观测器二次稳定和输入输出稳定的充分条件.最后通过数值算例表明了结论的有效性.
[1]Luders G,Narendra K.S.A new canonical form for an adaptive observer[J].IEEE Trans.on Automatic Control,1974,19(2): 117-119.
[2]Zhang Q.Adaptive observer for multiple-inputmultiple-output(MIMO)linear time-varying systems[J].IEEE Trans.on Automatic Control,2002,47(3):525-529.
[3]Vahedforough E,Shafai B.Design of proportional integral adaptive observers[C].In Proc.of the IEEE American Control Conference,2008.3683-3688.
[4]Jung J,Hwang J,Huh K.Optimal proportional-integral adaptive observer design for a class of uncertain nonlinear systems[C]. In Proc.of the IEEE American Control Conference,2007.1931-1936.
[5]Clegg J.A nonlinear integrator for servomechanisms[J].Trans.of the A.I.E.E,1958,77:41-42.
[6]Krishman K.R,Horowitz I.M.Synthesis of a nonlinear feedback system with significant plant-ignorance for prescribed system tolerances[J].International Journal of Control,1974,(4):689-706.
[7]Beker O,Hollot C,Chait Y,et al.Fundamental properties of reset control Systems[J].Automatica,2004,40:905-915.
[8]Guo Y,Wang Y,Xie L,etal.Stability analysis and design of reset systems:Theory and an application[J].Automatica,2009,45 (2):492-497.
[9]Nei D,Zaccarian L,Teel A.R.Stability properties of reset systems[J].Automatica,2008,44:2019-2026.
[10]Paese D,Franco C,Llorente S,etal.Resetadaptive observers and stability properties[C].In Proc.of the 18th IEEEMediterranean Control Letters,2010.1435-1440.
[11]Paese D,Ba~nos A,Sagues C.Optimal resetadaptive observer design[J].System and Control Letters,2011,60(10):877-883.
[12]玉强,郭艳平.广义线性系统容许性的新判据[J].青岛科技大学学报,2009,30(3):281-282.
[13]Dai L.Singular Control Systems[M].Berlin:Springer-Verlag Berlin Heidelberg,1989.
[14]Boyd S,Ghaoui L.E,Feron E,etal.LinearMatrix Inequalities in System and Control Theory[M].Philadelphia:Society for Industrial and Applied Mathematics,1994.
【责任编辑 牛怀岗】
Stability Analysis for Reset Observers of Singular System
ZHANG Xiao-qian,WU Bao-wei,LIBao-ping
(College of Mathematics and Information Science,Shaanxi Normal University,Xi'an 710062,China)
The stability of reset observers of singular system is investigated.By constructing Lyapunov functions,this paper provides the sufficient condition of quadratic and input-output stability for reset observers of singular system with linearmatrix inequalities(LMIs)and S-procedure.Then,a numerical example verifies the feasibility of proposed theorems.
singular system;reset observers;quadratic stability;linearmatrix inequality
O231
A
1009-5128(2014)03-0010-06
2013-12-11
国家自然科学基金资助项目:von Neumann代数上的非交换Hp理论研究(10971123);陕西省自然科学基础研究计划项目:不确定时滞系统的稳定性和鲁棒H控制(SJ08A20)
张小茜(1988—),女,山东青岛人,陕西师范大学数学与信息科学学院硕士研究生;吴保卫(1963—),男,陕西西安人,陕西师范大学数学与信息科学学院教授,主要从事控制理论研究.
