页岩气生产数据联合分析方法研究与应用

王军磊，位云生，陈鹏，韩会平

(1.中油勘探开发研究院，北京 100083；2.中油长庆油田公司，陕西西安 710021）

页岩气生产数据联合分析方法研究与应用

王军磊1，位云生1，陈鹏2，韩会平2

(1.中油勘探开发研究院，北京 100083；2.中油长庆油田公司，陕西西安 710021）

生产数据分析方法集合了气藏工程和试井分析方法的优势，用以获取气藏动态信息、评价开发效果、预测气井产量，但受制于页岩气特殊的流动机理和开发方式，使用单一模型解释结果往往具有很大的不确定性。针对此问题，建立了以流态识别、解析分析和经验分析为核心的包含多种数据分析方法的综合模型，同时利用拟压力、拟时间处理气井压力、产量等原始生产数据，并结合系统分析原理分析拟生产数据，分析过程多种方法相互验证，不断提高解释结果的可信度，形成有效的页岩气生产数据联合分析方法。矿场实例具体演绎了整个分析流程，得到了合理的气藏动态信息，在此基础上预测气井产量，为后期开发方案调整提供了可靠的理论支持。

页岩气；气井；拟变量；数据处理；数据分析；分析流程

引言

页岩气是一种典型的非常规油气资源，具有较高的勘探成功率和较大的开发风险［1－2］。随着近些年来水平井钻完井、分段压裂和微地震监测技术的提高，页岩气正在成为一种重要的现实替代能源。目前中国页岩气的发展正处在起步阶段，四川长宁、威远地区已获得工业气流［3］。页岩气藏储量规模大小、单井产能高低等关键性问题决定着页岩气是否具有商业开采价值。

生产数据分析方法是一种重要的气藏动态描述手段，集合了试井分析和气藏工程的优点，通过处理和解释气井产量、压力等生产数据，获得储层渗透率、表皮系数、裂缝长度、导流能力、单井控制储量等参数，预测气井产量变化规律，从而为改进气藏开发效果、降低气藏开发风险提供有力的技术保证，具有实用、可靠、经济的特点。

页岩气非线性流动特性和气井不稳定生产使得压力、产量随时间的变化规律复杂［4－5］，长时间的非稳态流动期导致采用单一分析模型获得的解释结果不确定性高、可信度低［6］。本文针对页岩气的流动和开发特征，利用拟函数和叠加函数处理原始生产数据，联合多种分析模型分析生产数据，通过矿场应用演绎分析流程，获得了合理的评价结果，为后期开发方案调整提供理论依据，最终形成一套有效的页岩气生产数据联合分析方法。

1 页岩气生产数据联合分析方法

页岩气数据分析方法不同于常规方法，主要原因是其复杂的赋存及渗流机理［7－8］，包括气体从有机质颗粒或黏土表面的解吸、介质超低的渗透率、介质的应力敏感性、体积压裂形成复杂缝网结构的空间多尺度性以及气体的非达西流动效应等。

生产数据分析方法将气井生产过程中记录的产量、压力等信息进行分析处理，获取由这些信息反映出的地层特性。受制于页岩气特殊的渗流机理、复杂的开发方式和低质量、低分辨率的生产数据，目前仍没有一种完全成熟可靠的数据分析模型。联合多种分析模型分析气井数据，可以相互制约、验证，降低解释结果的不确定性，具体分析方法见图1。

通过步骤1～3筛选出合适的生产数据。生产数据分析方法使用的数据多，贯穿井的整个生命周期，但数据分辨率低、“噪音”大，数据源的质量决定了评价结果的可靠性，故在分析数据前需要评价、检查、剔除低质量的生产数据。对于一组原始的生产数据，需要对其进行诊断分析：①评价数据质量的可靠性，包括产量和压力数据、储层和流体参数、完井及增产措施等；②检查数据相关性，包括产量—压力、产量—时间和压力—时间的数据相关性检查；③初步诊断，主要是数据检查和整理，剔除错误数据。

图1 页岩气生产数据联合分析方法

利用步骤4～5中的数据分析模型分析气井产量、压力等数据，获得气藏、气井相关参数，这也是数据分析方法的核心部分。利用步骤6中的解析分析模型，通过调整参数拟合气井生产历史，以预测气井动态。在步骤7中，利用经验分析模型与解析分析模型进行相容性评价调整。

2 数据分析模型

数据分析模型包括流态识别模型、解析分析模型和经验分析模型。其中，流态识别模型是数据分析的基础。解析分析模型遵循系统分析原理，即正反问题：正问题，建立并求解一系列假定数学模型的标准信息(如理论公式、曲线图版)；反问题，利用实际系统反映出的信息(如产量、压力)与标准信息对比、拟合，确定出未知系统属于哪种已知系统。经验模型没有严格的理论推导，通过观察大量生产数据预测气井产量递减规律，预测结果不确定性大。

2.1 流态识别模型

流态指气体在地层中的流动特征，能够反映气井结构、气藏属性、缝网结构、气体物性等特征，流态识别是数据分析中最重要的步骤，贯穿整个分析流程。受气体高压物性、非达西流动、应力敏感和变产量生产等非线性影响，页岩气井原始生产数据变化规律复杂，将生产数据转换为拟压力、叠加拟时间或物质平衡拟时间后能清晰地反映出数据间的关联性。

使用各类诊断模型(如修正压力与物质平衡拟时间的双对数图版)识别气体流态(图2)。不同的流态在诊断图版上有不同的曲线特征，总体上气体流态可分为两大部分：非稳态流动段和拟稳态流动段。其中，非稳定流动阶段生产数据主要受气井结构和地层属性影响，拟稳态阶段生产数据主要受地层非均质性和地层边界控制。

2.2 解析分析模型

2.2.1 线性回归分析

图2 分段压裂水平井流态变化规律

在正确识别流态的基础上利用解析分析模型定量分析生产数据。线性分析类似于常规试井分析，将生产数据处理为产量修正的拟压力差Δm*/qgsc和物质平衡拟时间tca*或叠加拟时间，利用拟变量间的变化规律，结合相应的诊断工具确定流态，根据不同流态对应的线性关系式获得裂缝及气藏属性参数。常见流态的线性关系及参数计算公式见表1，处理后的数据在半对数、双对数或平方根等诊断图版下将呈现线性关系。表1中：L、r、x为长度，m；h为地层厚度，m；w为裂缝宽度，m；xf为裂缝半长，m；φ为地层孔隙度；t为时间，h；ta为拟时间，h；pR为平均地层压力，MPa；pi为原始地层压力，MPa；pw为井底压力，MPa；m为拟压力，MPa；K为渗透率，10－3μm2；q为产量，104m3/d；μgi为原始地层压力下的气体黏度，mPa·s；cti为原始地层压力下的综合压缩系数，MPa－1；T为地层温度，K；Gp为地质储量，108m3；求和项为Duhamel叠加时间；mBL、mL、mE、mR为对应流态的直线斜率；下标BLS、LS、LS分别表示双线性流、线性流、径向流；A、B表示椭圆流常数。

表1 常见流态的线性关系式

2.2.2 典型图版分析

典型图版分析类似于现代试井解释方法，基于某一特定的数学模型得到无量纲典型曲线及相应诊断曲线，将处理后的生产数据与典型曲线拟合获得相关参数。与线性分析方法不同的是，典型曲线通常同时拟合多个流态，这样可以相互制约，降低分析结果的不确定性。

在Fetkovich、Blasingame、Agrwal等学者［9－11］基础上，Wattenbarger［12］建立线性流模型，Bello［13］将裂缝网络看作双重介质，提出双线性流模型，Brown针对不同区域的流动能力，将体积压裂区(SRV)区内水力裂缝线性流、裂缝间地层线性流，裂缝端部SRV区外地层的线性流概括为三线性流模型［14］。(多)线性流模型更接近于气体在SRV内的实际流动，能够有效分析页岩气井生产数据，同时近年来也有学者开始使用多重介质模型描述页岩气在多尺度流动空间中的流动规律。

2.3 经验分析模型

2.3.1 幂律指数方法

直接应用Arps递减评价页岩气藏储量会产生很大误差。页岩气在相当长一段时间内处于非稳态流动阶段，Ilk以整个渗流期为研究对象，重新定义递减率D，进而得到不同于传统双曲递减的幂律型指数递减模型［15］。其中早期非稳态流动期主要受it影响，晚期拟稳态流动阶段受D∞t影响。

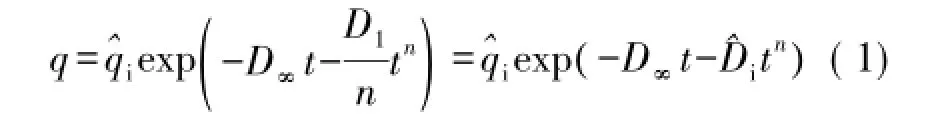
式中：D1为时间为1 d时对应的递减常数，d－1；D∞为时间趋于无穷大时对应的递减常数，d－1；i为递减常数，定义为D1/n；n为无量纲时间指数；为初始流量，104m3/d；t为时间，d。

2.3.2 合成方法

根据递减指数b变化规律［16］，用解析模型分析非稳态数据得到地层渗透率和表皮系数，用经验模型分析拟稳态数据获得递减参数b、Delf和qelf，预测产量。以线性流为例［12］，t＜telf时的非稳态流和t＞telf时的拟稳态流对应的产量公式分别满足：

式中：qelf为非稳态流量，104m3/d；b'为直线截距，10－4m－3·d。

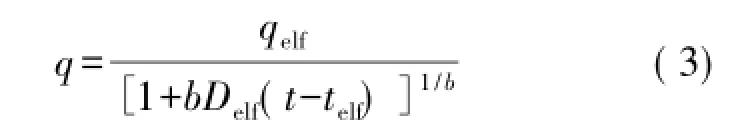
式中：b为Arps无量纲递减指数；Delf为线性流结束时刻递减常数，d－1；q为拟稳态流量，104m3/d；telf为线性流结束时间，d。

3 矿场实践

以四川盆地某国家级页岩气先导试验区中的某口水平井为例演绎生产数据分析方法。该区块中页岩储层致密，发育丰富的微米—纳米级孔隙，石英、长石等脆性矿物含量高，易于压裂改造。该井改造水平段长1 045 m，改造段数为10段，自2011年1月投产，生产时间为805 d，累计产气量为0.053×108m3。原始地层压力为16.3 MPa，地层温度为65℃，厚度为39.7 m，孔隙度为5%，含气饱和度为65.25%，Langmuir体积为3 m3/t，Langmuir压力为2.8 MPa。使用CH4物性参数，原始气体压缩系数为0.024 6 MPa－1，原始气体体积系数为0.003 95。

3.1 生产数据筛选及处理

按步骤1～3筛选生产数据，按式(7)、(8)处理数据。其中拟时间和物质平衡拟时间中涉及的平均地层压力通过地质储量迭代算法获得［17］。

3.2 生产数据分析

式中：Lf为裂缝半长，m；nf为裂缝条数。

由于主要流态是非稳态线性流和拟稳态流，按步骤5，将相关参数代入Wattenbarger无量纲定义(12)、(13)，对参数进行微调(＜10%)，与典型曲线拟合效果良好，见图4。

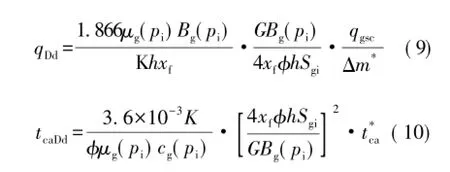
式中：Bg为气体体积系数；qDd为无量纲产量；tcaDd为无量纲物质平衡拟时间；Sgi为原始含气饱和度； Δm*为拟生产压差，MPa。

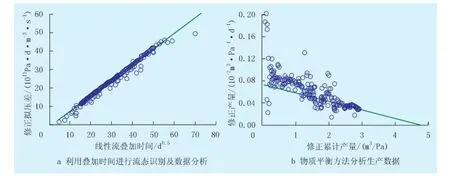
图3 线性回归分析模型

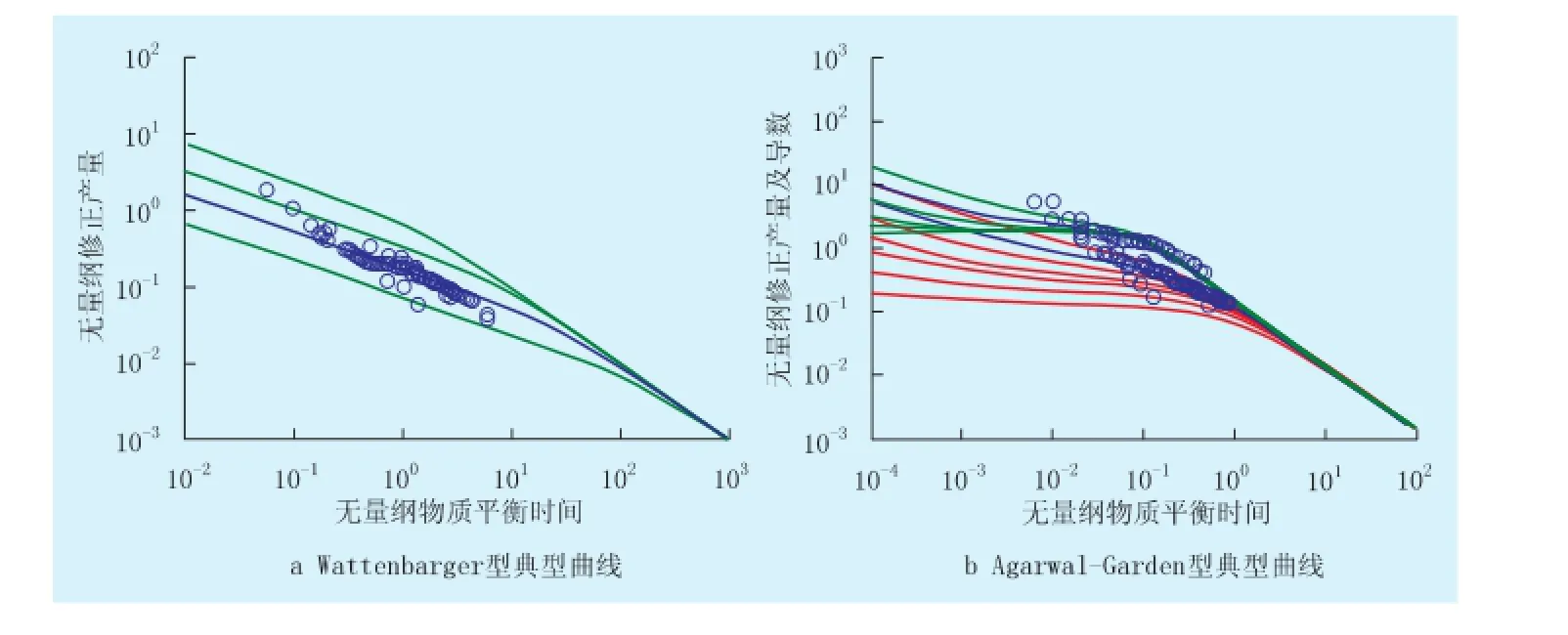
图4 典型曲线分析模型

同理使用Agarwal－Gardenr图版，对应的大裂缝穿透比(xf/re=0.5)拟合结果也预示着长时间的线性流动期。

每种分析模型都有多个解释结果，不同模型间相互调整、验证，可以降低解释结果的不确定性，最终评价结果见表2。

表2 多种分析模型解释结果

以上分析结果仅仅考虑了气体高压物性、解吸和气井变产量生产的影响，重新定义拟压力和拟时间函数［4］能够进一步研究气体非达西流动和介质应力敏感性对数据分析的影响。

3.3 气井产量预测

基于解析分析模型，利用物质平衡方程联立拟稳态气井产能方程进行页岩气产能预测［19］，20 a内的气井产量变化规律见图5a。气井保持4.82 MPa恒压生产，产量随时间递减，且递减率逐渐减小，直到后期保持相对稳定，最终采收率为25.1%。气藏可采储量集中在生产早期，主要来自孔隙中储存的自由气，生产后期主要来自吸附态的解吸气。由于拟稳态阶段生产数据过少，经验分析模型不确定性大，使用b=0.0，0.1，1.0，2.0四组参数预测气井产量，对比解析预测模型(表3)，发现经验指数型递减(b=0)较为接近，提高了解析预测结果的可信度。

图5 气井生产规律预测

气藏弹性采收率仅取决于气井流压，而预测期内的气藏采收率取决于气井流压和气体渗流阻力。提高气藏渗透率、增大气井与地层接触面积能够有效减小渗流阻力，但需要大型的体积压裂，而在合理配产基础上，降低气井压力能够充分发挥气体弹性能量，增加气体流动势能和气体解吸量(图6)，从而提高页岩气藏采收率(表4)。

表3 不同分析模型的预测结果(20a内)

表4 基于解析模型的预测结果

4 结论

(1)页岩气生产数据分析方法主要包括数据处理方法及数据分析模型。拟变量数据处理方法可以消除页岩气非线性流动的影响，是线性回归、典型曲线拟合等解析法的数据分析来源；幂律指数、解析合成等经验法直接拟合原始生产数据，预测气井产量变化规律。

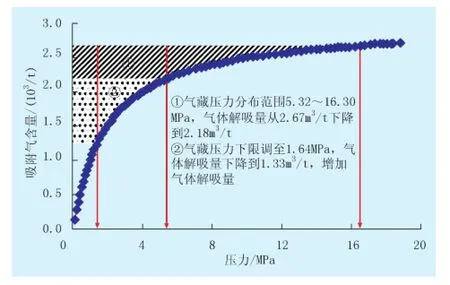
图6 等温吸附曲线

(2)解析分析模型可以解释地层渗透率、气藏地质储量等参数、预测气井产量，解释结果可靠性强，但模型受制因素多、数据处理过程繁复。经验分析模型方便灵活，不需要数据处理，但缺乏理论依据。集合不同分析模型的优点联合分析生产数据，不同模型间相互调整、验证，可以降低评价结果的不确定性，提高预测结果的可靠性。

［1］赵文智，董大忠，李建忠，等.中国页岩气资源潜力及其在天然气未来发展中的地位［J］.中国工程科学，2012，14(7)：46－52.

［2］张东晓，杨婷云.页岩气开发综述［J］.石油学报，2013，34(4)：792－801.

［3］王兰生，廖仕孟，陈更生，等.中国页岩气勘探开发面临的问题与对策［J］.天然气工业，2011，31(12)：1－4.

［4］Nobakht M，Clarkson C R，Kaviani D.New and improved methods for performing rate transient analysis of shale gas reservoirs［J］.SPE Reservoir Evaluation＆Engineering，2012，7(2)：335－486.

［5］Cipplla C L，Lolon E P，Erdle J C，et al.Reservoir modeling in shale gas reservoirs［J］.SPE Reservoir Evaluation＆Engineering，2010，8(3)：638－653.

［6］白玉湖，杨皓，陈桂华，等.页岩气产量递减曲线的不确定性分析方法［J］.石油钻探技术，2013，41(4)： 97－100.

［7］Civan F.Effective correlation of apparent gas permeability in tight porous media［J］.Transport in Porous Media，2010，8(2)：375－384.

［8］Wang F P，Reed R M，Katherine G.Pore networks and fluid flow in gas shales［C］.SPE124253，2009：1－16.

［9］Fetkovich M L.Decline curve analysis using type curves［J］.Journal of Canadian Petroleum Technology，1980，32(6)：1065－1077.

［10］Blasingame T A，McCray T L，Lee W J，et al.Decline curve analysis for variable pressure drop/variable flowrate systems［C］.SPE21513，1991：234－246.

［11］Agarwal R G，Gardner D C，Kleinsteiber S W，et al. Analyzing well produciton data using combined－typecurve and decline－curve analysis concepts［J］.SPE Reservoir Evaluation＆Engineering，1999，2(5)：478－486.

［12］Wattenbarger R A，Ei－Banbi A H，Villegas M E，et al. Production analysis of linear flow into fractured tight gas wells［C］.SPE39931，1998：1－12.

［13］Bello R O，Wattenbarger R A.Multi－stage hydraulically fractured shalegasratetransientanalysis［C］. SPE126754，2010：1－17.

［14］Brown M，Ozkan E，Raghavan R，et al.Practical solutions for pressure－transient responses of fractured horizontal wells in unconventional shale reservoirs［J］.SPE Reservoir Evaluation＆Engineering，2011，12(4)：663－676.

［15］Ilk D，Rushing J A，Perego A D，et al.Exponential vs. hyperbolic decline in tight gas sands－understanding the origin and implications for reserve estimates using Arps’decline curves［C］.SPE116731，2008：1－18.

［16］Kupchenko C L，Mattar L.Tight gas production performance using decline curves［C］.SPE114991，2008：1－20.

［17］John L，Wattenbarger R A.Gas reservoir engineering［M］.Texas：SPE Inc，1996：346－349.

［18］Ertekin T，King G R，Schewerer F C.Dynamic gas slippage：a unique dual－mechanism approach to the flow of gas in tight formations［J］.SPE Formation＆Evaluation，1986，1(6)：43－52.

［19］徐兵祥，李相方，Haghighi M，等.页岩气产量数据分析方法及产能预测［J］.中国石油大学学报：自然科学版，2013，37(3)：119－125.

编辑刘兆芝

TE33

A

1006－6535(2014)03－0007－07

10.3969/j.issn.1006－6535.2014.03.002

20131022；改回日期：20140319

国家科技重大专项“天然气开发关键技术”(2011ZX05015)

王军磊(1986－)，男，2012年硕士毕业于中国地质大学(北京)油气田开发工程专业，现为中国石油勘探开发研究院油气田开发工程专业在读博士研究生，从事渗流力学和气藏工程方面的研究工作。