用代数方法探讨四阶幻方的解

杨俊平，孟宪涛

（1.大连海洋大学，应用技术学院 辽宁 大连 116300；2.沈阳师范大学 数学与系统科学学院，沈阳 110034）

0 引 言

幻方为中国人所发明，早在汉朝就开始了三阶幻方的研究［1－3］。而我国南宋时期著名数学家杨辉则是对四阶幻方开展较为系统研究的第一人。他在所著的《续古摘奇算法》中给出了极为巧妙的四阶幻方构造方法：先将1～16这16个数排列成图1a，然后将四角位置的四个数按对角线方向两两对换，即1↔16，4↔13。再将位于中心位置2×2方阵的4个数按对角线方向两两对换，即10↔7，11↔6。对换后即得图1b，则图1b称为杨辉四阶幻方的阴图。对阴图1、2两行互换，3、4两行互换，即得图1c，图1c称为杨辉四阶幻方的阳图。注意到图1b、图1c中的每一行、列和对角线上的四数之和均为34，此处称34为四阶幻方常数。

和三阶幻方不同，四阶幻方的数量众多，且构造方法也不唯一，甚至可以用矩阵运算生成幻方：用0，1，2，3作为元素构造矩阵

由此矩阵即得图2幻方，且图2幻方为异于图1b、图1c的四阶幻方［4］。

幻方的研究一般包括寻求幻方的全部解和幻方特性的研究［5－7］。本文通过建立四阶幻方的约束方程组，利用代数方法得出四阶幻方解的约束条件，并结合试验方法给出四阶幻方的求解举例［8－10］。

1 约束条件

图2 矩阵运算产生的幻方

在图1b、图1c和图2中，给出了四阶幻方的3种形式，或称为是四阶幻方的3个解。

一般地设图3为四阶幻方的一个解，则有如下约束方程组成立，

图3 四阶幻方的一般形式

此处｛a11，a12，…，a44｝＝｛1，2，…，16｝。

对方程组（1）的增广矩阵进行初等变换得到对应的同解方程组

其中a24，a32，a33，a34，a42，a43，a44为自由未知量。

由方程组（2）中的a21＋a24＝a32＋a33，及其在图3中位置的对称性可得

图4刻划了等式a21＋a24＝a32＋a33的意义，即位于垂线阴影部分的两数之和与位于斜线阴影部分的两数之和是相等的。同理由对称性可解释（3）中后3个等式的意义。

由式（2）中a11＝a24＋a34＋a42＋a43＋a44－34可得

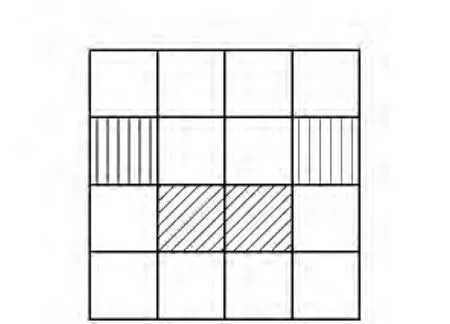
图4 方程（3）生成的幻方

考虑对称性，容易得出

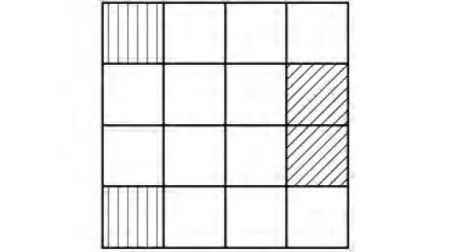
图5 方程（4）生成的幻方

式（4）的意义在于，凡图3中具有如图5相应位置关系的垂线阴影部分，两数之和与斜线阴影部分两数之和是相等的。

在图3中的4个顶角位置数字之和为34。

四阶幻方图3中，位于中心位置2×2方阵4个数之和为34（图6）。事实上，由式（3）可得

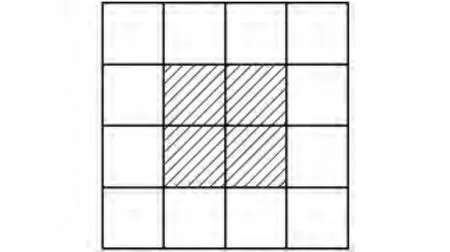
图6 中心位置之和为34的幻方

位于一条对角线顶点位置的2个2×2方阵子块4数之和相等（如图7）。事实上，由式（2）容易得出

同理有a11＋a12＋a21＋a22＝a33＋a34＋a43＋a44。

由于幻方常数为34，可知每一行每一列及每条对角线上的4个数中奇数（或偶数）的个数必定为偶数。

图7 四个字块相等的幻

2 应用约束条件探求幻方解

在利用约束条件求幻方解的时候，必须结合试验进行。下面给出求解举例。

已知杨辉四阶幻方阴图如图1b，由式（3）中的

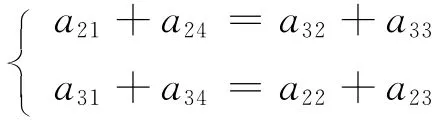
与式（4）中的

图8 “行变换”形成的幻方

对图1b进行“行变换”即得图8，则图8为图3一个解，且该幻方异于杨辉的阴图。

再在式（3）中选择

两式，同时在式（4）中选择

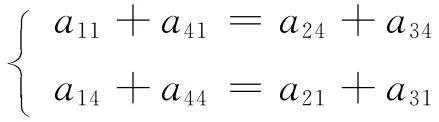
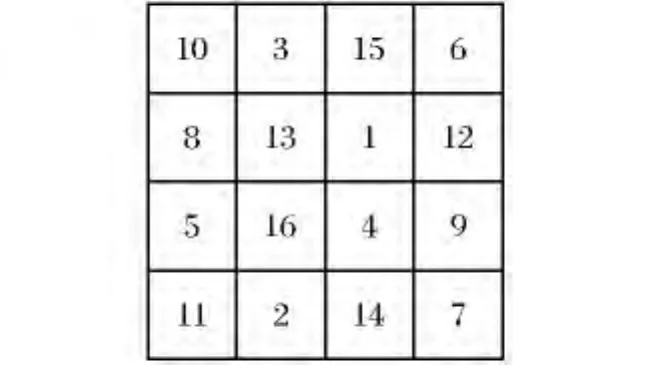
图9 “列变换”形成的幻方

并利用其对图8“列变换”，得图9，则图9为图3的一个异于图1b与图8的一个解。

若图3为四阶幻方的一个解，则按四阶方阵转置方法得到的仍是幻方的解。又若图3四阶幻方的一个解，则图3按顺时针（或逆时针）方向旋转90°所得到的仍然是幻方的解。

3 结 语

在上述实例中，笔者利用式（3）、式（4）分别对已知幻方进行“行变换”与“列变换”而得到3个新的幻方。这种由一个已知幻方构造新的幻方的方法不是唯一的［11－13］。

此外，可将一个已知幻方的一、二两列互换，再三、四两行互换，则生成的幻方为基本幻方；又可将一个已知幻方的一、三两列互换，再将二、四两行互换，或者先一、三两列互换，再一、三两行互换，等等，得到的都是基本幻方［14－15］。但需注意的是，在2次行、列对换的时候要考虑到对称性。可见由已知幻方生成新的幻方的方法是很多的。

［1］吴鹤龄.幻方与素数——娱乐数学两大经典命题［M］.北京：科学出版社，2008.

［2］许莼舫.古算趣味［M］.北京：中国青年出版社，1955.

［3］钱宝琮.中国数学史［M］.北京：科学出版社，1964.

［4］刘秀峰.多重幻方的构造与若干问题研究［D］.汕头：汕头大学，2010.

［5］孙宏安.杨辉算法［M］.沈阳：辽宁教育出版社，1997.

［6］李冠林，顾大全.幻方的实现方法研究［J］.微型电脑应用，2010，26（1）17－18.

［7］刘玉君.Turbo码中幻方交织器的研究与设计［J］.信息工程大学学报，2006，7（4）：291－395.

［8］吴鹤龄.幻方及其他［M］.北京：科学出版社，2005：51－55.

［9］杨富锋.构造奇次同心幻方的一种方法［J］.数学的实践与认识，2006，36（5）：192－199.

［10］徐丹丹，顾秀松，张学斌.特殊四阶幻方的变换群［J］.运筹与管理，2010，19（2）：104－108.

［11］祝宝满，龚和林.非素数阶幻方的构造［J］.数学的实践与认识，2008，38（15）：207－214.

［12］陈剑南.素数阶均衡完美幻方若干问题初探［J］.计算机工程与应用，2009，45（21）：179－182.

［13］姜伟，刘彦佩.几类4－正则平面图的最小折数纵横扩张［J］.沈阳师范大学学报：自然科学版，2007，25（2）：129－134.

［14］欧阳录.最佳拉丁方与高级原幻方［J］.数学理论与应用，2001，21（3）：22－28.

［15］汪沸，姚华胜.幻方构建的一种方法［J］.黄山学院学报，2009，11（3）：28－32.