基于主从博弈的两部门并行系统的效率评价

许 皓，孙燕红，卞亦文

（1.安徽大学商学院，安徽合肥 230039；2.中国科学技术大学管理学院，安徽合肥 230026；3.上海大学悉尼工商学院，上海 201800）

基于主从博弈的两部门并行系统的效率评价

许 皓1，孙燕红2，卞亦文3

（1.安徽大学商学院，安徽合肥 230039；2.中国科学技术大学管理学院，安徽合肥 230026；3.上海大学悉尼工商学院，上海 201800）

本文研究了一类典型并行系统的效率评价问题：（1）决策单元由两个并行的子单元组成；（2）在整个系统中，某一子单元居于主导地位，另一子单元居于从属地位；（3）两个子单元之间存在部分共享的投入资源，且无法明显区别该资源在不同子单元之间的分配比例。在分析决策单元整体效率及内部子单元效率的基础上，基于主从博弈思想，提出一种能同时确定系统整体效率及内部子单元效率的评价方法，该方法能够在评价系统效率的同时，实现共享资源的有效分配。最后，采用一个实例分析说明了所提方法的合理性和有效性。

数据包络分析（DEA）；主从博弈；并行系统；共享投入

1 引言

生产与服务系统往往呈现两大共性：具有复杂的内部结构和多种投入/产出要素［1］；此外，系统中所有子系统往往共享某些公共资源。一种典型的系统是具有共享资源的两部门（子系统）并行结构的生产或服务系统。例如，高校中的教学与科研两大职能部门，为完成各自职能，都投入一定的专职教师和业务经费，且两部门还共同使用一些共享的投入要素，如身兼两职的教师和图书馆、实验室以及后勤服务人员等资源［2］；银行的销售与服务部门，除了各自人员、设备和经费外，也会使用公共的设备终端和服务支持人员等公共资源［3］。这类系统往往呈现一个显著特征：某个部门优于另一个部门而处于主导地位，如研究型高校的科研往往优于教学而处于主导地位，教学型高校的教学则优于科研而处于主导地位；银行主要以销售各种理财产品及放贷而获取利润，因而销售部门往往居于主导地位。因此，在这类系统中，居于主导地位的部门对整个系统的运行效率具有重要影响。低投入高产出的运行效率是任何生产与服务系统追求的目标，为分析这种具有共享投入的两部门并行系统的效率，必须同时考虑各部门自身的投入/产出要素、部门共享资源（投入）以及部门之间的关系。

数据包络分析（Data Envelopment Analysis，DEA）是一种评价具有多投入多产出系统效率的重要方法。在现有的DEA文献中，有众多关于并行系统的效率评价方法，这些方法主要分为三类：网络DEA方法［4-7］、多部门DEA方法［3，8-12］和关联DEA方法［13-15］。网络DEA方法假定各子单元独立运行，且效率评价时各子单元拥有自身的一组投入/产出权重；多部门DEA方法假定系统效率是各子单元效率的加权组合，并假定各子系统的投入/产出权重各不相同；关联DEA方法则认为系统中相同的投入/产出应该赋予相同的权重。此外，段永瑞等［16］基于规模收益、组内合作与组间合作假设，提出了三种并行系统效率评价的DEA模型。杨锋等［17］在研究并行系统前沿生产能力的基础上，提出了并行系统的乘数和包络模型，此后，又进一步研究了子单元之间存在中间要素的情形［1］。葛虹等［18］则讨论了现有主要并行DEA模型及选择应用问题。毕功兵等［19］在并行系统中引入了环境变量，并提出了相应模型。赵萌［20］在并行系统中引入了时间因素，构建了动态并行DEA模型，研究了中国制造业的生产效率问题。

现有文献中，部分研究探讨了并行系统的共享投入要素问题。Beasley［2］在研究教学与科研效率时引入了共享的经费要素，并假设一种共享要素在整个系统中具有同样的权重，提出了一种非线性的评价模型；而Cook［3，8］和Jahanshahloo等［11-12］则假定共享投入在不同部门中具有不同的权重。陈凯华等［21］基于多部门DEA方法，在固定和可变规模收益下分别研究了共享投入并行系统的效率评价与分解问题。这些研究主要是在现有并行系统效率评价的DEA模型中，引入共享投入，并在不同假设下研究了效率评价与资源分配的问题。但现有研究，并未考虑系统各子单元之间的相互关系，无法揭示出对系统效率具有主导作用的关键部门和关键要素，因而难以合理评价并行系统的效率，也难以为系统效率改善和资源配置提供科学的决策依据。

并行系统中不同部门的作用差异和相互关系导致其效率评价问题变得更加复杂，而共享资源的配置则进一步加剧了问题的复杂性。为有效解决这种并行系统的效率评价问题，本文基于非合作主从博弈思想，提出一种两部门共享投入的并行系统效率评价方法，其能在有效处理部门之间关系的基础上，合理评价部门及系统的效率，并实现资源的有效配置。最后，采用一个银行实例分析说明了所提方法的合理性和有效性。

2 并行系统的效率评价问题

为了便于问题描述，假定存在n个相互独立的并行系统，又称为决策单元（Decision Making U-nits，DMU），系统的组成结构如图1所示。

图1 并行系统的组成结构

图1中，一个系统由两个平行的子系统A和B组成；XA和YA分别是子系统A的投入向量和产出向量，XB和YB分别是子系统B的投入向量和产出向量；XS是子系统A和B共享的投入向量。需要说明的是，子系统A、B的投入向量和产出向量中可能既包含同种类型的投入/产出要素，又包含独有的投入/产出要素。

为了分析此类并行系统的效率，作出如下假设：（1）子系统A和B之间存在非合作主从博弈关系，即某个子系统在整个系统中居于主导地位；（2）共享投入是两个子系统共同使用的资源，但在实际运行过程中无法明显区分各子系统的使用量；（3）同种投入/产出要素具有相同的权重。为了构建系统的效率评价模型，进一步假设子系统A使用共享投入XS的份额向量为αT，则子系统B使用共享投入XS的份额向量为（1-α）T。

根据各子系统的投入/产出指标，可直接定义各子系统的效率。子系统A和B的效率定义为：

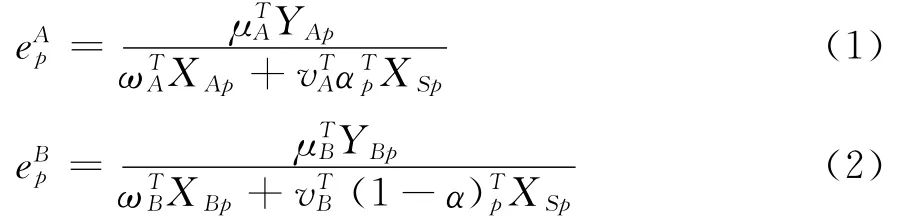
对每个子系统和整个系统而言，均可建立相应的效率评价模型，但这种模型构建方式无法体现子系统之间及子系统与整个系统之间的效率关系。为此，定义并行系统的效率为各子系统效率的加权和［1，17］，则并行系统的效率评价模型为：

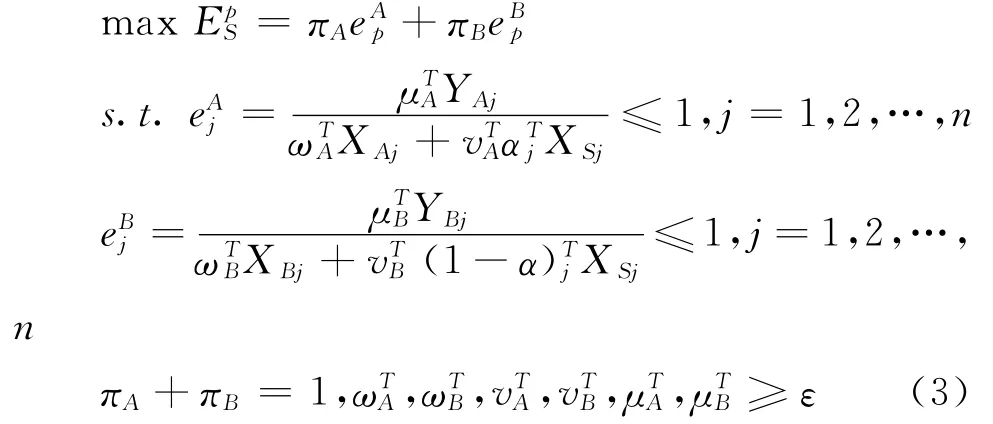
模型（3）中，πA和πB分别是子系统A和B的权重；ε是一个任意小的正数向量，不妨设其元素皆为0.000001。由于共享投入指标在整个系统中的权重应保持一致，即vTA=vTB，则设vT=vTA=vTB。子系统权重可据其资源消耗情况进行度量［1，22］，即：

在实际使用中共享资源的分配应有一定的限制条件［3］，不失一般性，这里假设≤≤；其中和分别为共享资源分配比例向量的下限和上限向量。另外，根据式（4），模型（3）中的约束条件πA+πB=1成为冗余约束。基于上述假设和分析，模型（3）可变换为下列规划模型：

模型（5）实际上是子系统A和B联合决策的情形，通过求解模型（5）虽然可得到子系统和整个系统的效率，并能确定共享资源的分配比例，但其不能体现各子系统在整个生产系统中的具体作用。为此，必须寻求新的效率评价方法。

3 基于主从博弈的并行系统的效率评价

在实际问题中，并行系统的子系统并不一定能完全实现联合决策，往往存在某子系统占优的情况，在这种情形下，系统效率评价必须考虑子系统的作用与地位。基于非合作博弈的思想，假设图1中某个子系统处于主导地位，而另一个子系统居于从属地位，则整个系统效率评价可视为两阶段非合作主从博弈的效率评价问题［22］。在构建效率评价模型时，首先考虑居于主导地位的某个子系统i（i=A或B），求解该子系统的效率值，然后将其作为约束条件引入整个系统的效率评价模型中，通过求解该模型可得另一子系统的效率值，以及各共享投入资源在不同子系统之间的分配比例。

为构建具体的效率评价模型，首先假设i=A，即子系统A居于主导地位，则其效率评价模型为：T

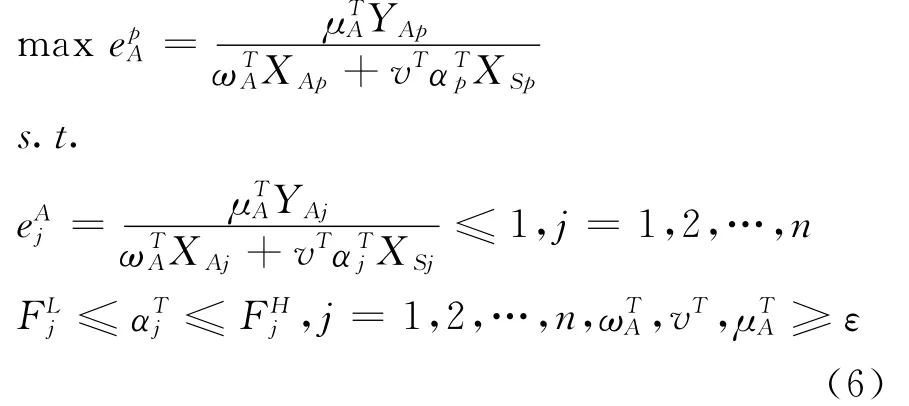
求解模型（7）即可得到子系统A的效率值。由于A在整个系统中居于主导地位，故首先确定子系统A的效率值，其次在评价整个系统效率时，保持子系统A的效率值不变。设ep*A为子系统A的最优效率值，将其作为约束条件引入到并行系统效率评价模型中，则模型（5）可转化为下列规划模型：

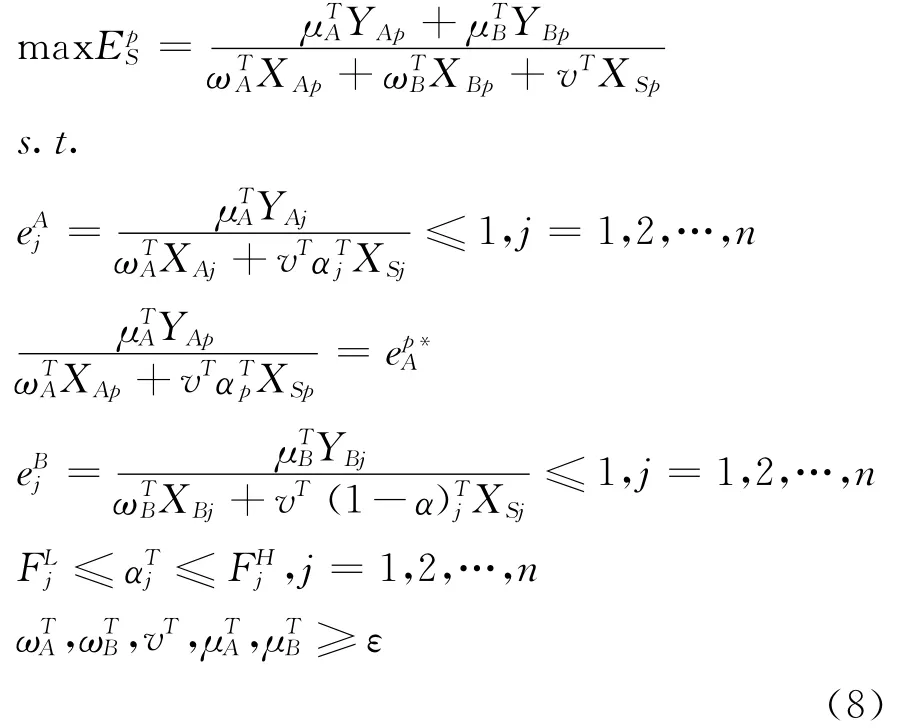
与模型（6）类似，设ρTj=vTαTj，模型（8）可转化为下列线性规划：

由模型（9）可知，通过求解该模型可得并行系统的效率值，以及各投入/产出指标的权重；依据这些指标的权重值可直接得到子系统B的效率值，以及各共享投入在A与B两个子系统中的分配比例。

若i=B（子系统B居于主导地位），此时的效率评价思想和评价过程与i=A时类似，这里不再详述。

4 实例分析

为分析说明本文所提方法的合理性和有效性，本节采用Cook等［3］中的加拿大某商业银行20家支行的实例进行详细分析。各支行可视为一个由销售与服务两部门组成的并行系统，两部门有各自的投入/产出指标，以及部分共享的投入指标，具体指标见表1。

表1中，FSU和FST是两部门共享的投入资源，且这两种资源在生产过程中难以区分其在不同部门之间的使用量，各指标的具体数据如表2所示。

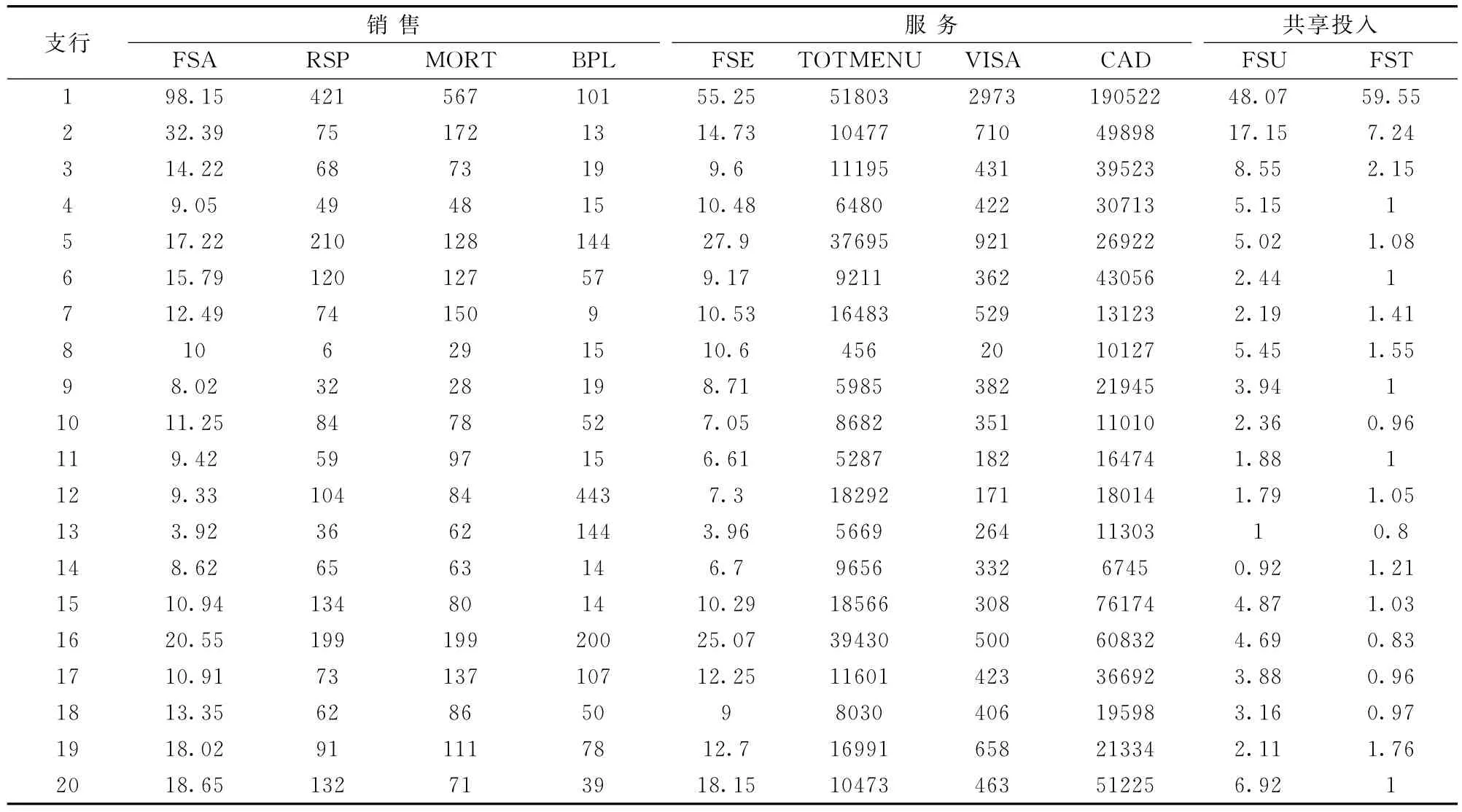
表2 某银行20家支行相关指标的具体数据

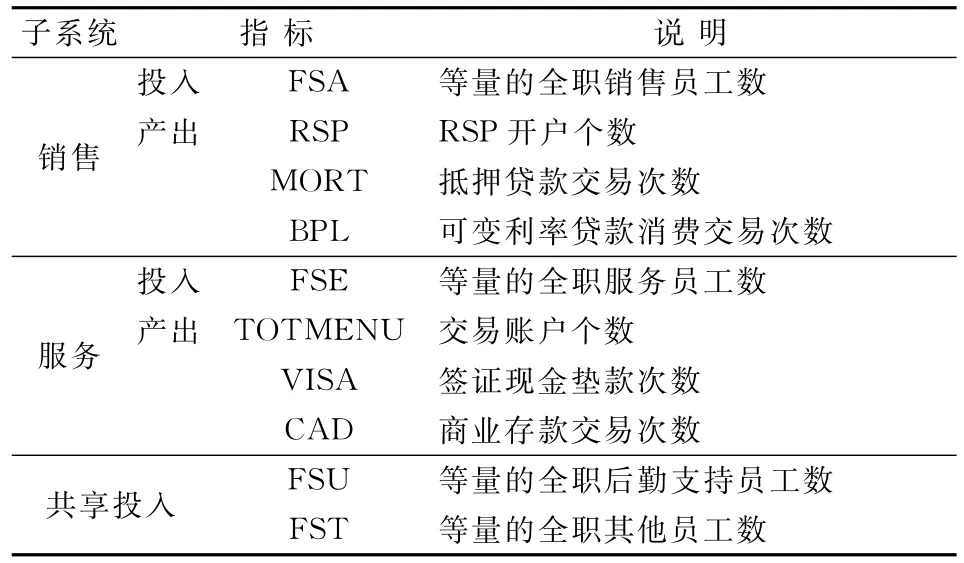
表1 某银行20家支行的投入/产出指标a

由于商业银行所有的业务收入主要来源其金融业务产品销售（即开户、资产抵押、担保和非担保贷款等），可认为销售部门在所有支行系统中居于主导地位，而服务部门居于从属地位。为了有效确定共享投入在不同部门之间的分配比例，必须设定其有效变化范围，设0.25≤αTj≤0.75［3］，即αTj中的每个元素都在［0.25，0.75］之间变化。为求解各支行及其销售、服务部门的效率，并实现共享投入的有效分配，基于本文所提出的方法，首先求解销售部门的效率，其次根据并行系统整体效率评价模型求解各支行及服务部门的效率，同时确定共享投入的分配比例。各支行与其下属部门的效率值，以及共享投入的分配比例值如表3所示。

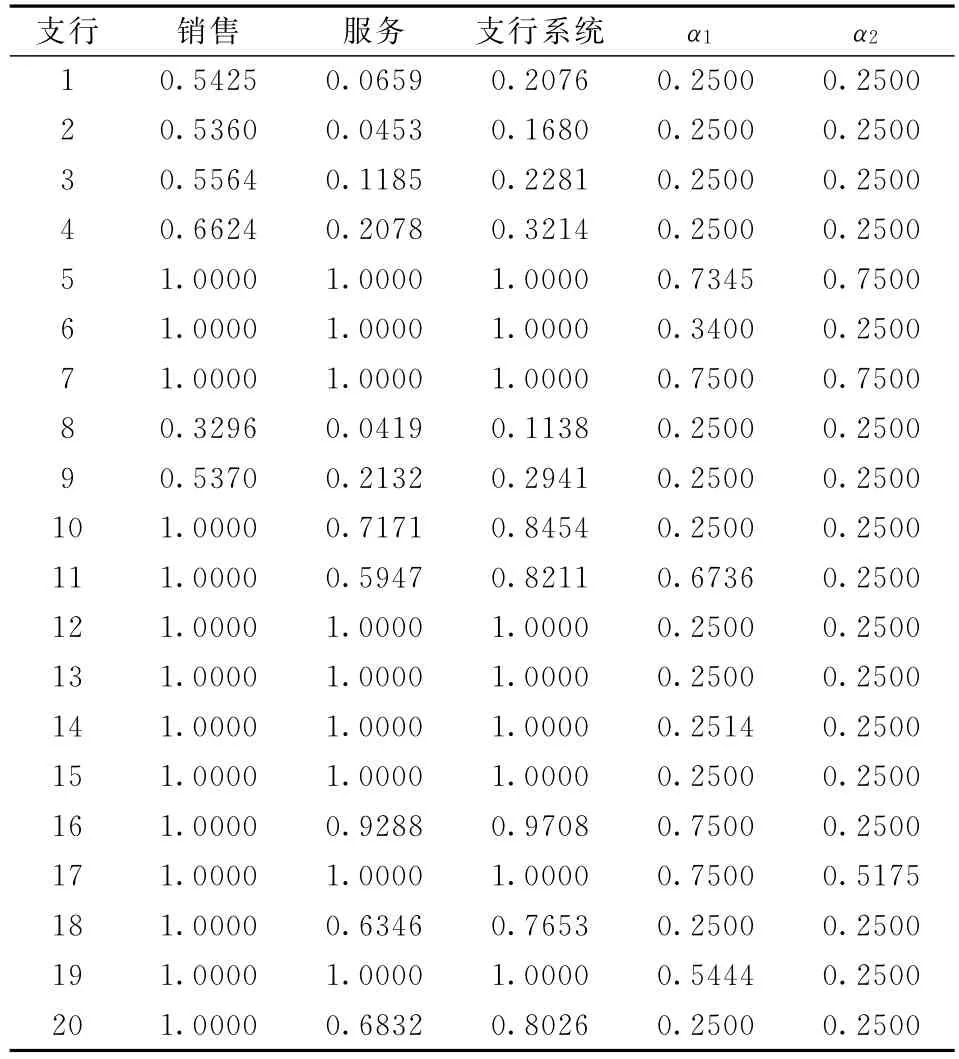
表3 某银行20家支行及部门的效率值

表3中，α1和α2分别表示在支行中销售部门所分配的共享投入FSU和FST的比例值。由表3的数据结构可以看出：（1）支行系统有效，当且仅当其下属两个部门都有效，例如支行5-7，12-15，17和19；反之，当支行下属某部门有效时，整个支行未必有效，例如支行10和11，其销售部门有效，但其服务部门无效，则整个支行是DEA无效的；这些结果说明，若要提高支行的运作效率，必须制定合适的策略和措施，同时提高销售部门与服务部门的运作效率，才能真正实现整个支行的效率优化；（2）销售部门居于主导地位，其平均效率值（0.8582）大于服务部门的平均效率值（0.6626）；（3）通过求解支行系统的效率值，可以有效得到共享投入在不同部门之间的分配比例。

值得一提的是，实例分析中可考虑各部门权重变化对部门及支行系统效率值的影响，具体方法是将部门权重作为约束条件引入并行系统的效率评价模型即可，这里也不再赘述。

基于上述分析可知，文中所提方法不仅能有效区别并行系统内部各部门的作用与地位，而且有效实现了系统及部门之间的效率评价和共享投入资源的分配。

5 结语

在实际并行生产系统中，其下属部门往往共享部分投入资源，且某个部门在整个系统中居于主导地位，为有效解决这一类系统的效率评价问题，本文提出了一种具有两部门并行系统的效率评价的DEA方法。首先，假定某个部门居于主导地位，则优先评价该部门的效率；然后，将该部门效率作为约束条件引入整个系统的效率评价模型中，通过求解该模型即可得到另一个部门的效率及整个系统的效率值，并同时能得到共享投入资源在不同部门之间的分配比例。银行的实例分析说明本文所提方法的合理性和有效性。文中所提方法能够在区别决策单元内部并行子单元的作用与地位情况下，有效实现决策单元、内部子单元的效率评价及共享资源的分配。

［1］夏琼，杨锋，梁樑，等.非独立并联生产系统的DEA效率评价研究［J］.管理科学学报，2012，15（7）：20-25.

［2］Beasley J E.Determining teaching and research efficiencies［J］.Journal of the Operational Research Society，1995，46（4）：441-452.

［3］Cook W D，Hababou M.Sales performance measurement in bank branches［J］.Omega，2001，29（4）：299 -307.

［4］Färe R，Grosskopf S.Productivity and intermediate products：A frontier approach［J］.Economics Letters， 1996，50（1）：65-70.

［5］Färe R，Grosskopf S.Network DEA［J］.Socio-Economic Planning Sciences，2000，34（1）：35-49.

［6］Yang Yinsheng，Ma B，Koike M.Efficiency-measuring DEA model for production system with k independent subsystems［J］.Journal of the Operations Research Society of Japan，2000，43（3）：343-353.

［7］Castelli L，Pesenti R，Ukovich W.DEA-like models for the efficiency evaluation of hierarchically structured units［J］.European Journal of Operational Research，2004，154（2）：465-476.

［8］Cook W D，Hababou M，Tuenter H J H.Multicomponent efficiency measurement and shared inputs in DEA：An application to sales and service performance in bank branches［J］，Journal of productivity Analysis，2000，14（3）：209-224.

［9］Cook W D，Green R H.Multicomponent efficiency measurement and core business identification in multiplant firms：A DEA model［J］.European Journal of Operational Research，2004，157（3）：540-551.

［10］Amirteimoori A R，Kordrostami S.DEA-like models for multi-component performance measurement［J］. Applied Mathematics and Computation，2005，163（2）：735-743.

［11］Jahanshahloo G R，Amirteimoori A，Kordrostami S. Multi-component performance，progress and regress measurement and shared inputs and outputs in DEA for panel data：An application in commercial bank branches［J］.Applied Mathematics and Computation，2004，151（1）：1-16.

［12］Jahanshahloo G R，Amirteimoori A，Kordrostami S.Measuring the multi-component efficiency with shared inputs and outputs in data envelopment analysis［J］.Applied Mathematics and Computation，2004，155（1）：283-293.

［13］Kao C.Efficiency measurement for parallel production systems［J］.European Journal of Operational Research，2009，196（8）：1107-1112.

［14］Kao C.Efficiency decomposition in network data envelopment analysis：A relational model［J］.European Journal of Operational Research，2009，192（3）：949-962.

［15］Kao C，Hwang S N.Efficiency measurement for network systems：IT impact on firm performance［J］. Decision Support Systems，2010，48（3）：437-446.

［16］段永瑞，田澎，张卫平.具有独立子系统的DEA模型及其应用［J］.管理工程学报，2006，20（1）：27-31.

［17］杨锋，梁樑，凌六一，等.并联结构决策单元的DEA效率评价研究［J］.中国管理科学，2009，17（6）：157-162.

［19］毕功兵，冯晨鹏，丁晶晶.考虑环境属性约束的平行结构DEA模型［J］.中国管理科学，2011，19（5）：79-86.

［20］赵萌.中国制造业生产效率评价：基于并联决策单元的动态DEA方法［J］.系统工程理论与实践，2012，32（6）：1251-1260.

［21］陈凯华，官建成.共享投入型关联两阶段生产系统的网络DEA效率测度与分解［J］.系统工程理论与实践，2011，31（7）：1211-1221.

［22］Chen Yao，Cook W D，Li Ning，et al.Additive efficiency decomposition in two-stage DEA［J］.European Journal of Operational Research，2009，196（3）：1170 -1176.

Efficiency Evaluation of Parallel Systems with Two Components Based on Stackelberg Game Theory

XU Hao1，SUN Yan-hong2，BIAN Yi-wen3
（1.School of Business，Anhui University，Hefei 230039，China；2.School of Management，University of Science&Technology of China，Hefei 230026，China；3.Sydney Institute of Language&Commerce，Shanghai University，Shanghai 201800，China）

There exists a typical kind of efficiency evaluation problem for parallel systems，which has the following characteristics.Firstly，decision making unit（DMU）has two parallel components.Secondly，in any DMU，a component is in a dominant position，and another component living in a subordinate position. Lastly，some input resources are shared between two components and cannot be proportionally differentiated with each other.To address this kind of efficiency evaluation problem，a DEA approach is proposed to determine the efficiency of the overall system and internal components by analyzing the overall efficiency of the DMU and individual efficiency of each component，based on Stackelberg game theory.The proposed approach can not only evaluate the efficiencies of the whole system and its components，but also provide the allocation mechanism of the shared resources.A case of bank branches is presented to demonstrate the rationality and validity of the proposed approach.

Data Envelopment Analysis（DEA）；Stackelberg game；parallel system；shared input

C931

：A

1003-207（2014）05-0115-06

2012-10-15；

2013-12-30

国家自然科学基金资助项目（71371010，71101135，71101085）；上海市教委科研创新重点资助项目（12ZS099）

许皓（1964-），男（汉族），江苏江阴人，安徽大学商学院，教授，博士，研究方向：管理科学.