一种反映水驱极限的相渗曲线预测方法

于春磊

（中石化胜利油田分公司，山东 东营 257015）

引 言

目前中国水驱中高渗透油藏大多数已进入特高含水期，该阶段油藏不同区域间含水饱和度差异使储层非均质现象不断加剧[1-5]，并且出现了注水井周围和强水洗部位驱油效率高于室内实验的现象[6]。由于岩心实验与油藏在尺度上存在的巨大差异，相对油藏中注水井周围及主流线区域而言，室内岩心实验的驱替程度与油藏实际渗流过程存在巨大的差异，且该差异随着水驱开发不断加剧。这种驱替程度上的不足导致常规油水相渗曲线只能描述一定阶段而不能描述整个渗流过程，但关于相渗曲线的相关研究内容多集中在计算方法、影响因素等方面[7-12]，针对相渗曲线如何完整反映水驱过程的研究尚未见报道。笔者进行了多组高驱替程度的相渗实验，实验累计注水达到了1000倍孔隙体积。通过对实验结果统计分析，得出了油水相渗比值曲线变化规律，包括油水相渗比值曲线下弯时机分布规律和下完段数学表达式及其求解方法。建立了一套能够描述完整水驱过程的相渗实验计算方法，将室内模拟和油藏渗流的驱替过程统一起来，使之能够满足特高含水期油藏渗流规律描述的需要。

1 常规相渗应用中存在的问题

实验设备包括流体注入部分、岩心模型、围压控制部分、温度控制部分、压力检测部分以及出口计量部分。实验温度为50℃；模型采用胜利油田密闭取心岩样，岩心尺寸为 2.5 cm×2.5 cm×6.1cm 的圆柱状，渗透率为2100×10-3μ m2，孔隙度为31.5%；实验用水为氯化钾溶液，其矿化度为30000mg/L；实验用油为实验条件下黏度为36.49mPa·s的精制油。实验过程参照行业标准SY/T 5345-2007，结束条件由标准中注水30倍孔隙体积（或含水率到99.95%时）改为累计注水1000倍孔隙体积。

1.1 驱油效率的影响

通常水驱实验进行到30倍孔隙体积或者含水率达到99.95%之后，驱油效率不会再有大的变化。实际上，尽管含水率已经达到了极高值，但是随着注水倍数的增加，驱油效率仍然可以进一步增加。直至水驱结束时，驱油效率由30倍孔隙体积对应的61.1%增至1000倍孔隙体积对应的71.05%，增幅约11个百分点。常规相渗曲线无法反映增加的该部分驱油效率，造成油藏中强水洗区域剩余油饱和度描述存在误差。

1.2 非均质性的影响

油水两相渗流过程中，总液量可以表示为：

其中，油水流度和为含水饱和度Sw的函数：

式中：Ql为产液量，mL/min；Qo为产油量, mL/min；Qw为产水量, mL/min；A为渗流截面积，cm2；Kair为岩心空气渗透率，10-3μ m2；Kro为油相的相对渗透率；Krw为水相的相对渗透率，；Δp为驱替压差，KPa；L为岩心长度，cm；μo为油相的黏度，mPa·s；μw为水相的黏度，mPa·s；Sw为含水饱和度。

驱替过程中含水饱和度的变化引起油水流度和发生变化，对产液能力产生重要影响。图1为高倍相渗实验油水两相流度和随含水饱和度变化曲线。由图1可知，油水流度和随含水饱和度增加而增加。在特高含水阶段，油藏强水洗区域由于长期注水冲刷含水饱和度不断增加，使高渗区域渗流能力不断增强，含水饱和度差异对储层非均质性的放大作用成为层间或者平面矛盾的重要影响因素。但常规相渗曲线只能描述一定阶段的变化，高倍水驱实验中30倍孔隙体积对应流度和为208×10-3μ m2/mPa·s ，而1000倍孔隙体积对应油水流度和为1588×10-3μ m2/mPa·s，前者仅是后者的1/7，常规相渗曲线使层间或者平面矛盾存在低估的可能。

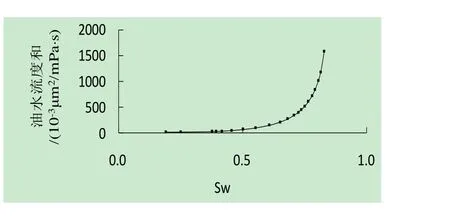
图1 油水流度和随含水饱和度变化

2 相渗曲线预测方法

2.1 油水相渗比值变化规律研究

图2为典型的相渗比值曲线，按照曲线形态可以分为3个阶段，常规相渗实验能够描述前2个阶段的变化规律，但不能完整地反映第3阶段的变化。针对第3阶段进行研究，建立下弯时机和下弯段的相关数学模型，从而实现常规相渗的外推预测。

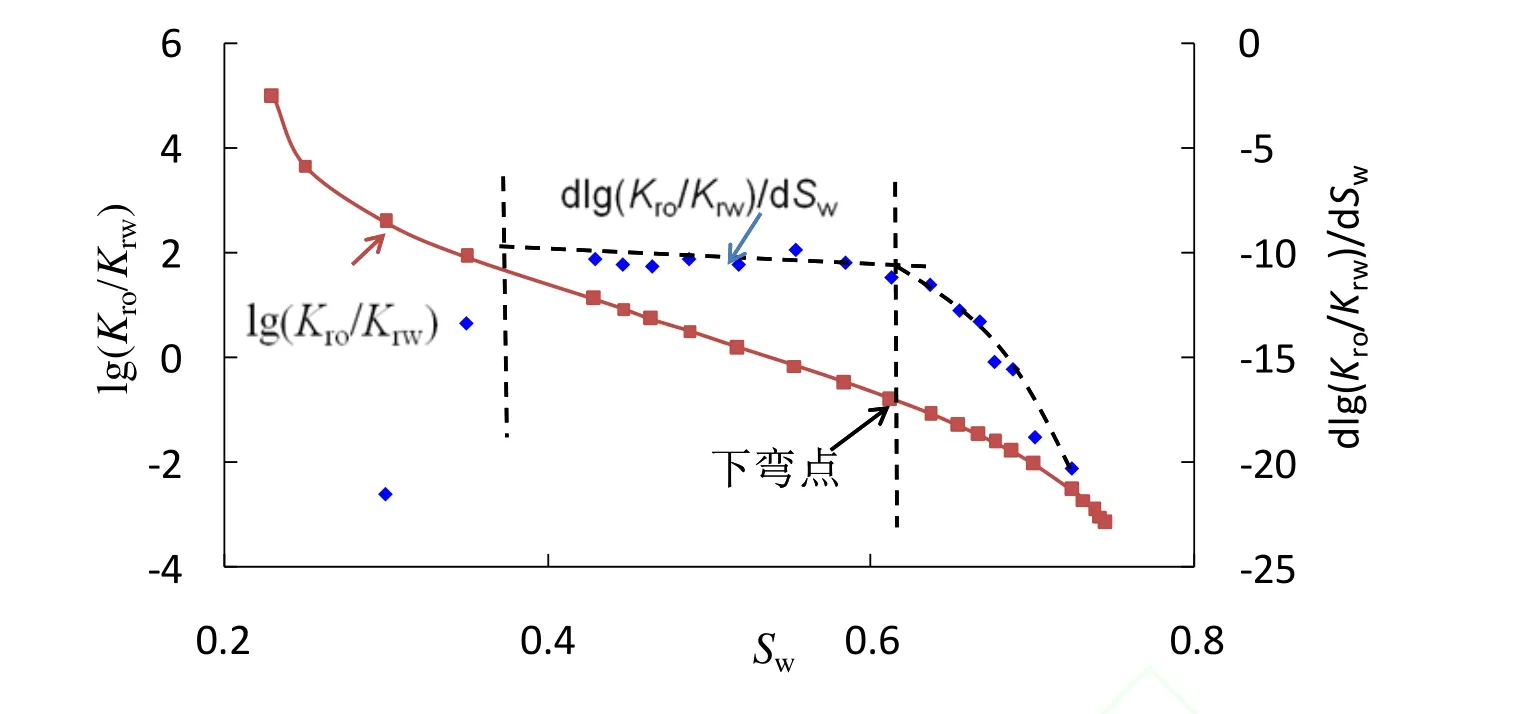
图2 相渗比值及其斜率变化

利用胜利整装油田多口密闭取心井共计124组岩心进行相渗实验，实验结果反映了不同渗透率级别及油水黏度比值的影响，见表1。

表1 样品相关参数分布范围

图3为实验的部分结果。由图3可知，当驱替到一定程度时油水相渗比值曲线普遍发生下弯。在多孔介质、流体性质及实验条件确定后，水驱的极限驱油效率是一定的，接近极限驱油效率的过程是剩余油结构及赋存方式持续变差的过程，因此越接近极限驱油效率值，原油的流动能力越差，油相渗透率与水相渗透率的比值越来小，且变化速度越来越快，当其变化超出了对数函数所描述的变化趋势，lg(Kro/Krw)—Sw曲线出现下弯现象。

（1）下弯时机分布规律。统计结果显示，第3阶段出现的时机存在一定的规律性。渗透率对下弯点影响较小，同一油水黏度比条件下，不同渗透率岩心相渗比值曲线下弯时机基本一致；下弯时机主要受油水黏度比的影响，油水黏度比（由于实验中水相黏度未发生改变，因此油水黏度比主要反映的是原油的黏度变化）越大，下弯点对应含水率越高。实验用岩心渗透率分布区间为 100×10-3～7000×10-3μ m2，原油黏度为 9.75～75.40mPa·s，岩心呈弱亲水状态，下弯点对应含水率分布范围为97.5%～99.0%。

（2）下弯段表征方法。所有的高倍驱替实验结果都表明：当含水率值大于实验油水黏度比对应的含水率时，油水相渗比值遵循式（3）的变化规律。

式中：R、m、n为相关常数。

2.2 预测方法

在对下弯时机和下弯段准确描述的基础上，高倍水驱相渗曲线可被计算出来。步骤：①30倍孔隙体积水驱油相渗实验（参照标准SY/T 5345-2007）；②根据实验油水黏度比计算出下弯时机对应的含水率；③根据下弯后的数据段，采用最小二乘法用式（4）进行拟合求解：

式中：x表示下弯后的第x个数据点，下标cal表示式（4）的计算值，下标obs表示实验观测值。取J值最小时对应的R、m、n值为最终解，得出Kro/Krw与Sw之间的变化关系。

水驱所能达到的残余油饱和度可由式（5）求出：

式中：Sor为残余油饱和度。

水相相对渗透率与含水饱和度关系在半对数坐标轴上近似呈线性变化，对水相相对渗透率曲线的预测可以按照30倍孔隙体积相渗曲线中水相相渗曲线变化趋势外推，达到所求残余油饱和度时的水相相对渗透率值作为水相相渗的端点值。根据水相相渗曲线和油水相渗比值曲线，求解出油相相渗曲线，从而得到完整的相渗曲线。

3 应用实例

该预测方法建立在渗透率为100×10-3～7000×10-3μ m2、原油黏度为9.75～75.40mPa·s的中高渗砂岩高倍水驱实验规律基础上，在类似条件的中高渗砂岩油藏中应用有较高的精度。

以4组岩心为例，实验条件与前文所述实验条件一致。4组岩心分别用不同黏度的原油进行实验，每组岩心驱替到1000倍孔隙体积，用上述计算方法对30倍孔隙体积的相渗数据进行计算，然后与1000倍孔隙体积水驱实验结果进行对比。图4为基于30倍孔隙体积相渗数据预测值与实验值的对比结果。由图4可知，油水相渗比值曲线的预测结果与实际变化值基本一致，预测的残余油饱和度值与水相渗透率端点值十分接近。表2为30倍孔隙体积预测值与1000倍孔隙体积实验值对比统计结果。由表2可知，相对误差均小于5%，在可接受的范围以内，证明该预测方法具有较高的准确度。

图4 油水相渗比值曲线预测与实验结果对比

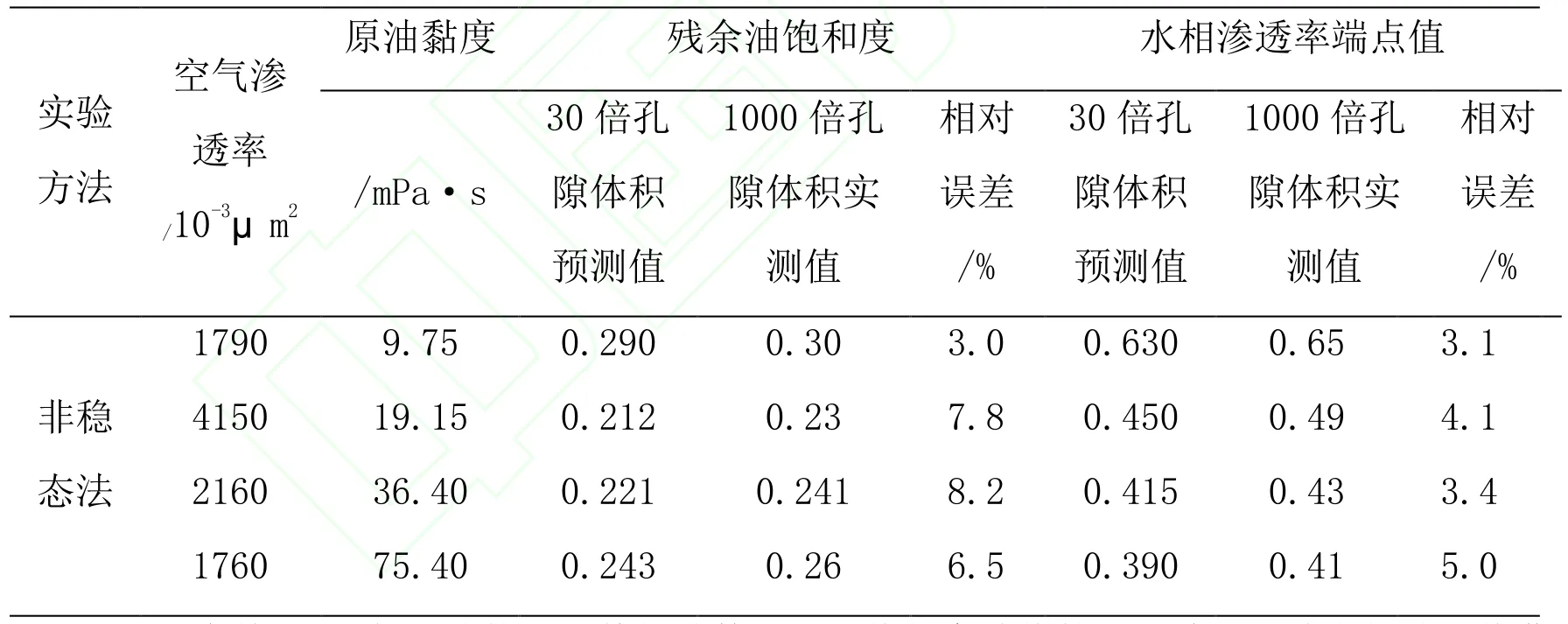
表2 30倍孔隙体积驱替预测值与1000倍孔隙体积驱替实验值对比统计

图4为基于30倍孔隙体积驱替相渗数据预测值与实验值的对比结果。油水相渗比值曲线的预测结果与实际变化值基本一致，预测的残余油饱和度值与水相渗透率端点值十分接近，误差在可接受的范围以内（表2），证明该预测方法具有较高的准确度。

4 结 论

（1）通过高倍相渗实验，对常规相渗在特高含水阶段油藏中应用存在的问题进行了分析，认识到常规相渗曲线只能描述一定阶段而不是整个水驱过程，特高含水期需要能描述长期注水冲刷作用的相渗曲线。

（2）对相渗比值曲线变化规律的研究，得出了相渗比值曲线下弯时机和下完段的数学表征方法，并提出了基于常规相渗数据预测高倍相渗曲线的方法。预测方法在渗透率为100×10～7000×10μ m、原油黏度为9.75～75.40mPa·s的中高渗砂岩油藏中具有较高的精度，可以满足工程计算的要求，对特高含水期油藏研究有积极的作用。

[1]安伟煜.特高含水期多层非均质油藏层间干扰因素分析[J].东北石油大学学报，2012，36(5)：76-82.

[2]于春生，李闽，乔国安，等.多层长岩心水驱油实验数值模拟研究[J].断块油气田，2007，14(4)：52-55.

[3]陈涛平，张志琦.非均质低渗透油层超低界面张力体系驱油方式[J].大庆石油学院学报，2009，33(5)：55-59.

[4]刘喆，崔英怀，杨传宏.非均质组合模型水驱油试验研究[J].吐哈油气，2009，14(1)：60-62.

[5]于春生，李闽，乔国安，等.纵向非均质油藏水驱油实验研究[J].西南石油大学学报，2009，31(1)：84-88.

[6]纪淑红，田昌炳，等.高含水阶段重新认识水驱油效率[J].石油勘探与开发，2012，39（3）：338-344.

[7]Johnson E F，Bossler D P，Naumann V O. Calculation of relative permeability from displacement experiments[J].Trans.AⅠME，1959，216：370-372.

[8]李克文，罗蔓莉，王健新.JBN方法的改进及相应的计算与绘图软件[J].石油勘探与开发，1994，21(3)：99-104.

[9]陈忠，殷宜平，陈浩.非稳态法计算油水相对渗透率的方法探讨[J].断块油气田，2005，12(1)：41-43.

[10]杨小平.精确计算相对渗透率的方法[J].石油勘探与开发，1998，25(6)：63-66.

[11]杨宇，周文，等.计算相对渗透率曲线的新方法[J].油气地质与采收率，2010，17(2)：105-107.

[12]李克文，戴志坚，江义容.稳定流方法与非稳定流方法的对比[J].石油勘探与开发，1995，22(1)：47-51.