城市交通与土地利用系统演化图景和结构研究

诸葛承祥，邵春福，高 健，孟 梦，计 寻

（北京交通大学 城市交通复杂系统理论与技术教育部重点实验室，北京 100044）

1 引言

国民经济的快速增长加快了城市化的进程，城市规模不断扩张，机动化进程加快，居民交通需求猛增，道路交通拥堵问题日益突出.国内外实践证明，城市交通与土地利用的一体化规划，从规划层面协同二者之间的关系，是从根源上解决城市交通问题的重要前提，是决定城市可持续发展的关键.国内外对城市交通与土地利用的研究较为广泛，相关的理论研究与成果可分为以下三方面：

（1）城市交通与土地利用系统相互影响研究.如孙胜阳以北京地铁1号线为例研究轨道交通对沿线土地利用的影响[1]；Debrezion G对荷兰房地产市场中轨道交通对房价的影响进行了研究[2].

（2）城市交通与土地利用系统的相协调研究.如谢秉磊对TOD下城市轨道交通与土地利用的协调关系进行了评价[3]；Yigitcanlar T提出了一个评价城市土地利用、环境和交通的可持续性发展的模型[4].

（3）城市交通与土地利用系统的互动关系模型研究.应江黔提出了关于交通运输与土地利用的综合模型的连续最优化及敏感性分析的基本框架[5]；Kakaraparthi S K利用UrbanSim仿真软件对美国德州奥斯汀的城市交通和土地利用系统的互动关系进行了建模[6].

总体而言，有关土地利用与交通系统之间存在相互影响、互动调节研究较多，但对两者相互影响、互动调节现象背后所隐藏的内在演化机理研究较为缺乏.本文将分别利用混沌理论和分形理论从时间序和空间序的角度揭示UTLU系统自组织演化的演化图景和结构复杂性.混沌理论和分形理论在城市交通领域的研究中应用较为广泛，混沌理论主要应用于短时交通流预测、智能交通系统、交通控制、交通系统预测等；分形理论主要应用于交通事故分析、交通网络分析、道路交通控制系统等.

每个城市的UTLU系统均有自身的特点，系统演化图景和演化结构各异，本文在演化实例研究中需用到历年的城市交通和土地利用数据，因此出于研究数据收集的难易程度考虑，仅以北京市为例进行研究，其它城市的研究方法类似.本文首先对UTLU系统的混沌特性进行判断，接着对系统的初值敏感性、分岔特性、混沌吸引子、内部随机性等特性进行分析，揭示系统的演化过程与图景；其次，以位序—规模分形模型对UTLU系统自组织演化结构进行评定.

2 基于混沌理论的UTLU系统演化图景研究

利用混沌理论揭示UTLU系统演化图景，首要问题是判断UTLU系统是否存在混沌现象.传统方法是选取表征UTLU系统演化的时间序列，计算其最大Lyapunov指数并进行判断，若最大Lyapunov指数大于0，则系统存在混沌现象，反之则无.相空间重构理论认为：系统的任一变量的演化是由与之相互作用的其它分量所决定，而这些相关分量的信息隐藏在任一分量的发展过程中.因此，可通过从某一分量的一批时间序列中提取和恢复出系统原来的规律，这种规律是一个系统在高维相空间下所展现的一种轨迹[7].在与本文相关的前期研究中，已利用协同学确定了北京市UTLU系统自组织演化的序参量为城市人口、机动车保有量和道路面积，三者共同决定了系统的演化方向.因此，本文在混沌特性的分析中，并非像传统想法一样只选择某一个序参量进行分析，而是选择三个序参量的“合并量”——系统协同度的时间序列作为研究对象.系统协同度可用来衡量系统的自组织协同演化程度高低.如表1所示为1979—2010年北京市UTLU系统的协同度.

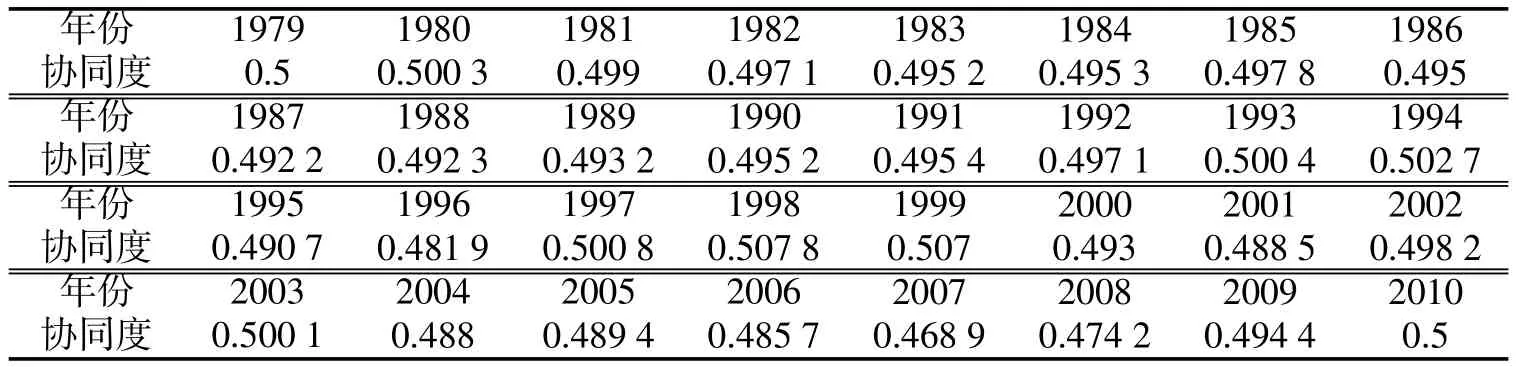
表1 1979—2010年北京市UTLU系统的协同度Table 1 Synergy degree of UTLU system from 1979 to 2010

本文将对系统协同度的时间序列进行分析，计算其最大Lyapunov指数.通过时间序列计算最大Lyapunov指数的方法主要有：Wolf法、Jocobian方法、P范数算法硷、奇异值分解法、小数据量计算法等.考虑到北京市UTLU系统协同度的时间序列数据量较少（1984—2010年），因此采用小数据量计算法.下面将对系统是否存在混沌现象进行判断，其具体计算步骤如下[8]：

Step2 分别采用G-P算法和自相关法确定延迟时间τ和嵌入维数m，经计算得到，北京市UTLU系统协同度的时间序列延迟时间τ=1，嵌入维m=4.

根据延迟时间τ=1和嵌入维数m=4重构相空间，结果如式（1）所示.

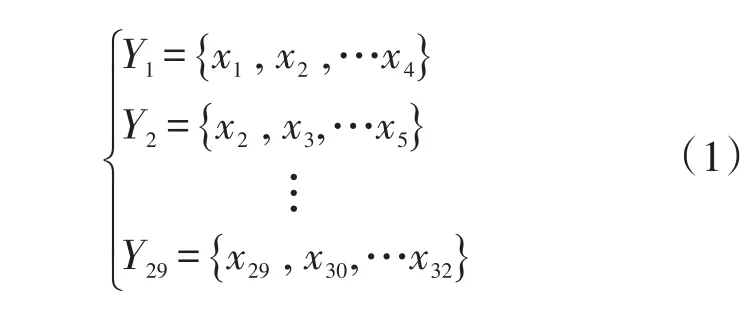
Step4 寻找相空间中每个点Yj的最近邻点，并限制短暂分离，即

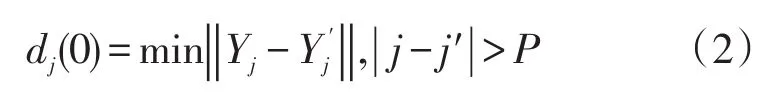
Step5 对相空间中每个点Yj，计算该邻点对(Yj,Y'j)之间i个离散时间步长后的距离dj(i)，计算公式如下：

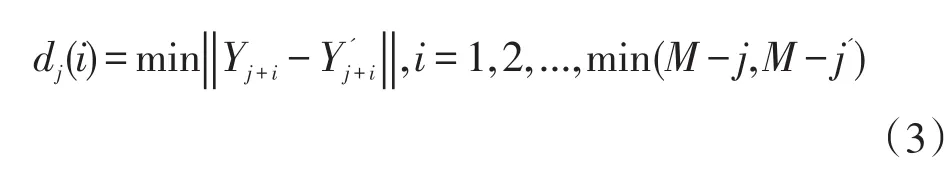
Step6 对每个i，求出所有 j的1n dj(i)平均值 y(i)，即

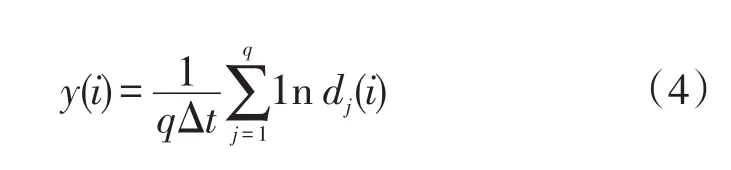
式中 q是非零dj(i)的数目，并利用最小二乘法作回归直线，所得直线斜率即为最大Lyapunov指数λmax.

根据Step4、Step5和Step6，计算得最小二乘法耦合结果如图1所示.其中最小二乘法求出的回归直线的斜率为0.192，即最大Lyapunov指数λmax=0.192，大于0，可推断北京市的UTLU系统存在混沌现象.

在判定北京市UTLU系统存在混沌特性后，根据混沌系统的初值敏感性、内在随机性、分岔、混沌吸引子、自相似等特性对系统进一步分析，揭示系统演化图景.其中初值敏感性揭示自组织优化措施的产生是系统演化的源泉；分岔揭示UTLU系统演化具有多种可能性；内在随机性揭示UTLU系统应动态规划和动态设计，并建立有效的反馈机制；混沌吸引子揭示UTLU系统的演化遵循收敛机制，收敛机制表现为选择，建立科学的选择机制是UTLU系统良好演化的关键；自相似性揭示UTLU系统演化不是组成元素简单放大的过程，而是层次不断增加的过程，且部分和整体之间具有自相似的特性[9].

图1 最大Lyapunov指数的小数据量法计算结果图Fig.1 The largest Lyapunov exponent calculated based on small-data method

3 基于分形理论的UTLU系统自组织演化结构研究

在系统自组织演化过程中，分形理论(Fractal Theory)可对系统的演化结构做出评价.系统演化的结构包括空间结构和等级结构两方面，前者以中心地的分形研究为标志，后者以位序，二者具有内在的逻辑关系，是分形城市体系最具代表性的研究领域，共同构成了城市系统空间复杂性的两个数量标志[10].考虑到采用前者进行研究对数据的要求较高，本文将以北京市为例，利用位序-规模分形模型对UTLU系统自组织演化结构进行评定.

3.1 基于位序—规模分形模型的UTLU系统自组织演化结构评价

分形理论主要用于解释和解决非线性世界中一些具有随机性和复杂性特征的现象和问题.在UTLU系统中，根据Zipf法则，城市的各个区县可按某种规模（如建设用地面积、道路交通网络、机动车保有量等）从大到小进行排序，则各个区县的位序r与区县规模P（r）之间存在以下关系：

式中 P（r）为城市区县规模位序中位次为r的城市规模；P1为首位区县规模；参数q为Zifp指数.

对式（5）两边取对数得

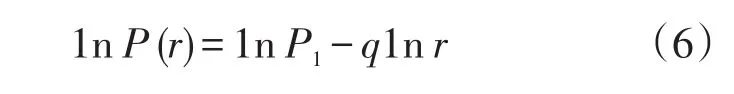
在城市地理学研究中，齐普夫(G K Zipf)定律也属于一种分形模型，因此，令A=，Df=1/q，则有

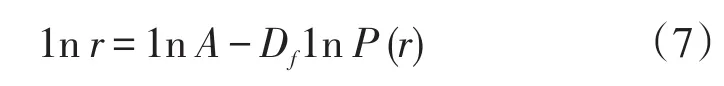
由此可见，Df和q均具有分维的性质，且互为倒数.分形维数Df和Zipf维数q的大小与空间分布等级规模结构相关[11]：

当D＜1（q＞1）时，规模分布趋于分散，城市的各区县分布差异较大，首位区县垄断性较强；

当D＞1（q＜1）时，规模分布均衡，中间位序的区县数目较多，整个城市体系发育比较成熟；

当D→0（q→∞）时，城市只有一个区县，为绝对首位型分布；

当D→∞（q→0）时，城市内各区县规模一样大，无差别.

下面对UTLU系统中位序—规模分形模型的应用步骤进行说明：

Step1 确定UTLU系统分析的规模对象；

Step2 若系统由n个区县构成，则按照上述某种规模进行大小排序，得到点序（P(r)，r），r=1,2,3…,n ；

Step3 绘制系统位序—规模双对数1n r-1n P(r)坐标图，并进行一元线性回归，得分形维数Df、Zipf指数q和相关系数.

3.2 基于位序—规模分形模型的UTLU系统自组织演化结构评价

分形理论认为相对规则的分析体在任何尺度下都是自相似的，具有严格的无标度性，而随机分析体在一定的尺度范围内则表现出自相似性.按照3.1节中介绍的位序—规模分形模型的应用步骤，本文以北京市的16个区县为研究对象，综合考虑规模对象数据获取的难易程度，以及是否能代表UTLU的演化程度，最终选定6个规模对象，其中4个为交通系统规模的指标：人均道路里程、人均道路面积、人均机动车保有量和人均公共停车设施；另外2个为土地利用系统规模的指标：人均建筑施工企业个数和人均建筑施工企业从业人员数.分别绘制上述6个规模对象的位序—规模双对数1n r-1n P(r)坐标图，利用一元线性方程对北京市的UTLU系统位序—规模模型进行回归分析，结果如表2所示.通过分析位序—规模对数相关系数，表明北京市UTLU系统规模对数与区县位序对数存在较强的相关性.

图2和图3分别为2008-2011年北京市区县交通系统和土地利用系统规模分维值变化图.从图2可知交通系统的规模变化如下：人均机动车保有量的分维值无明显变化；人均道路里程和人均道路面积的分维值在2010年均增加，表明北京市各区县人均道路里程和人均道路面积的规模趋于集中，差异变小，但分维值在2011年恢复到原先水平，即各区县人均道路里程和人均道路面积规模趋于分散，差异变大，恢复到原先水平；人均公共停车设施的分维值在2010年降低，表明北京市各区县人均公共停车设施的规模趋于分散，差异变大.从图3可知土地利用系统的规模变化如下：人均建筑施工企业个数的分维值变化不明显，人均建筑施工企业从业人员的分维值在2010年均减少，表明北京市各区县人均建筑施工企业从业人员的规模趋于分散，差异变大.

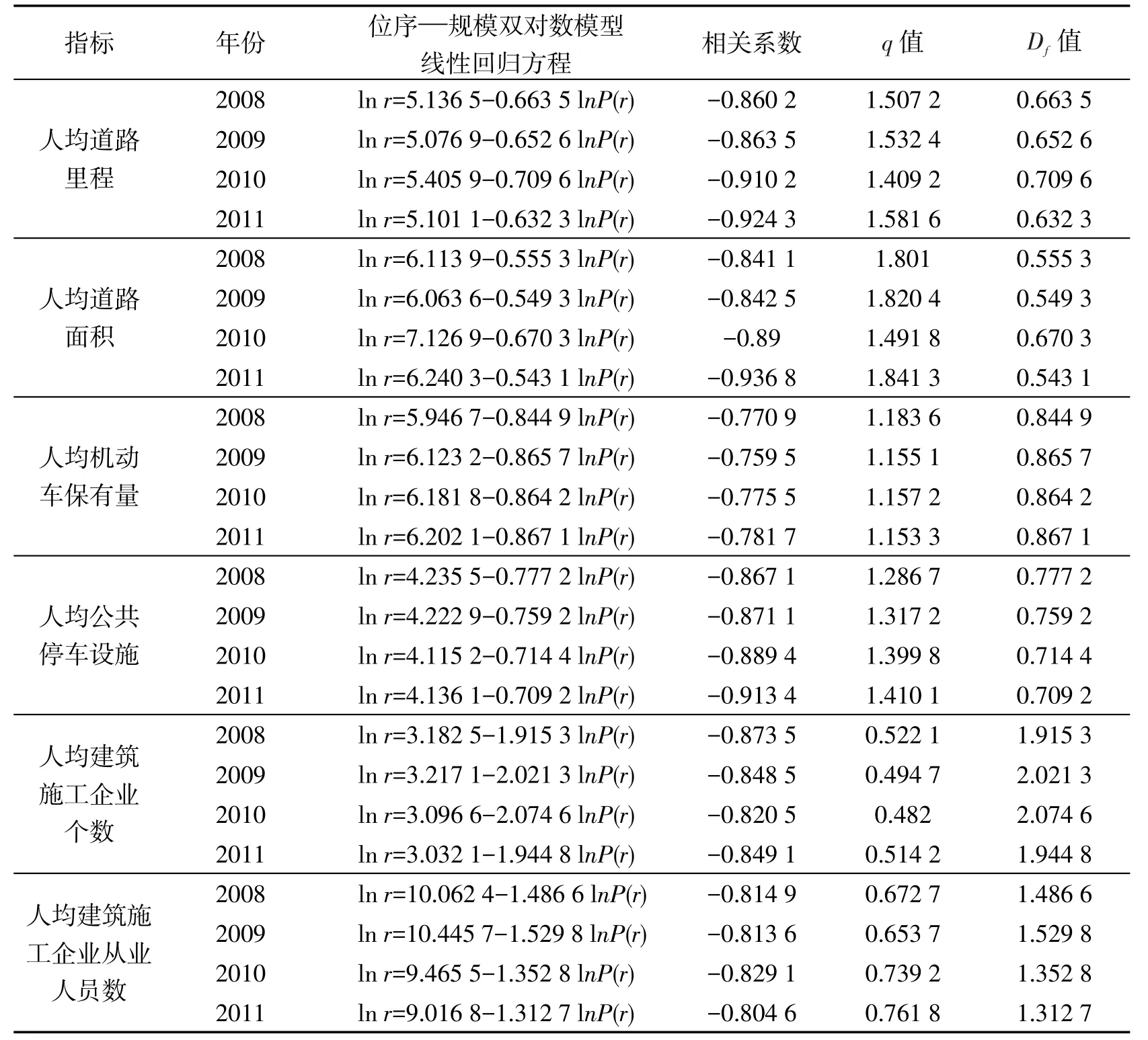
表2 2008-2011年北京市区县UTLU系统位序—规模分形模型线性回归分析结果Table 2 Linear regression results of Rank-Size model for UTLU system of districts in Beijing from 2008 to 2011

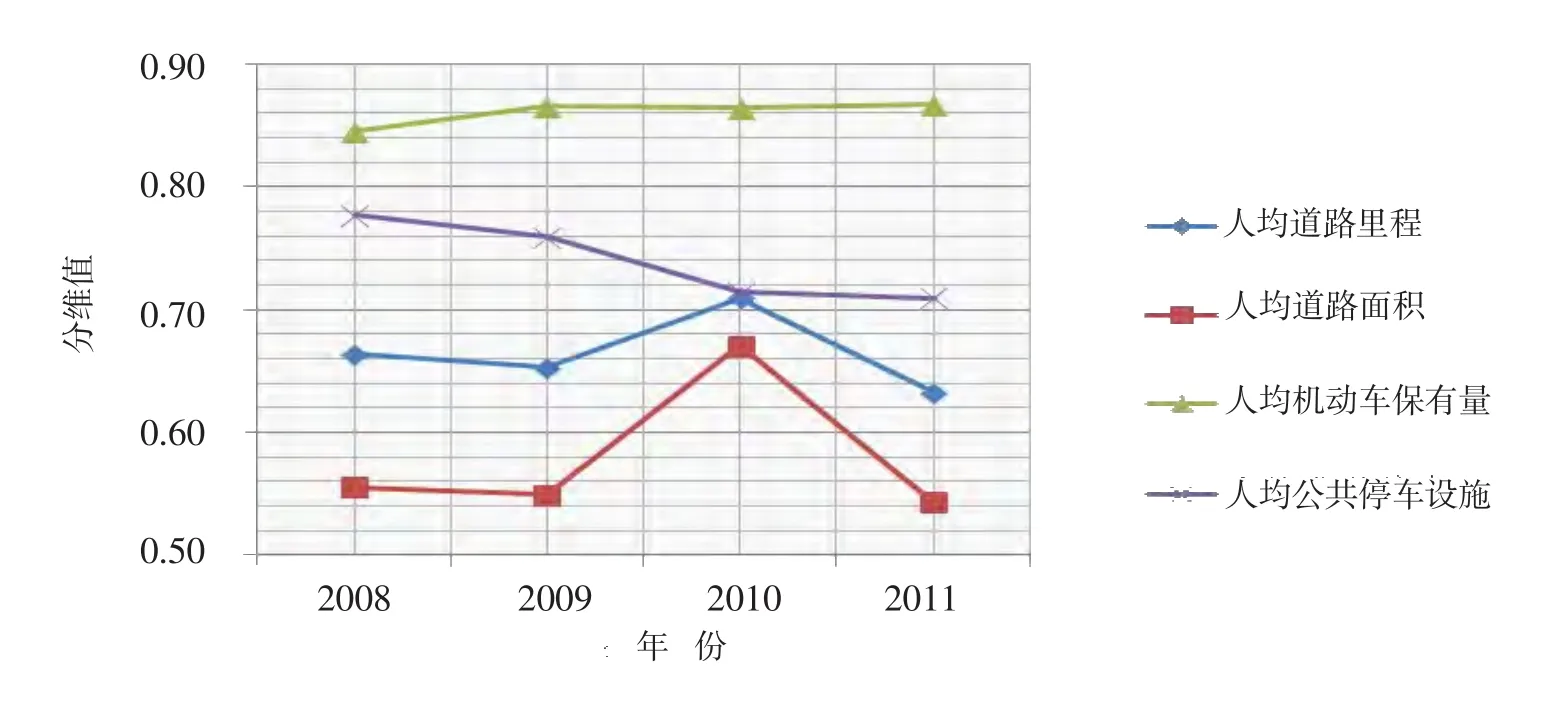
图2 2008-2011年北京市区县交通系统规模分维值变化图Fig.2 The change of fractal dimension value of the transportation system scale in Beijing’s districts and counties from 2008 to 2011

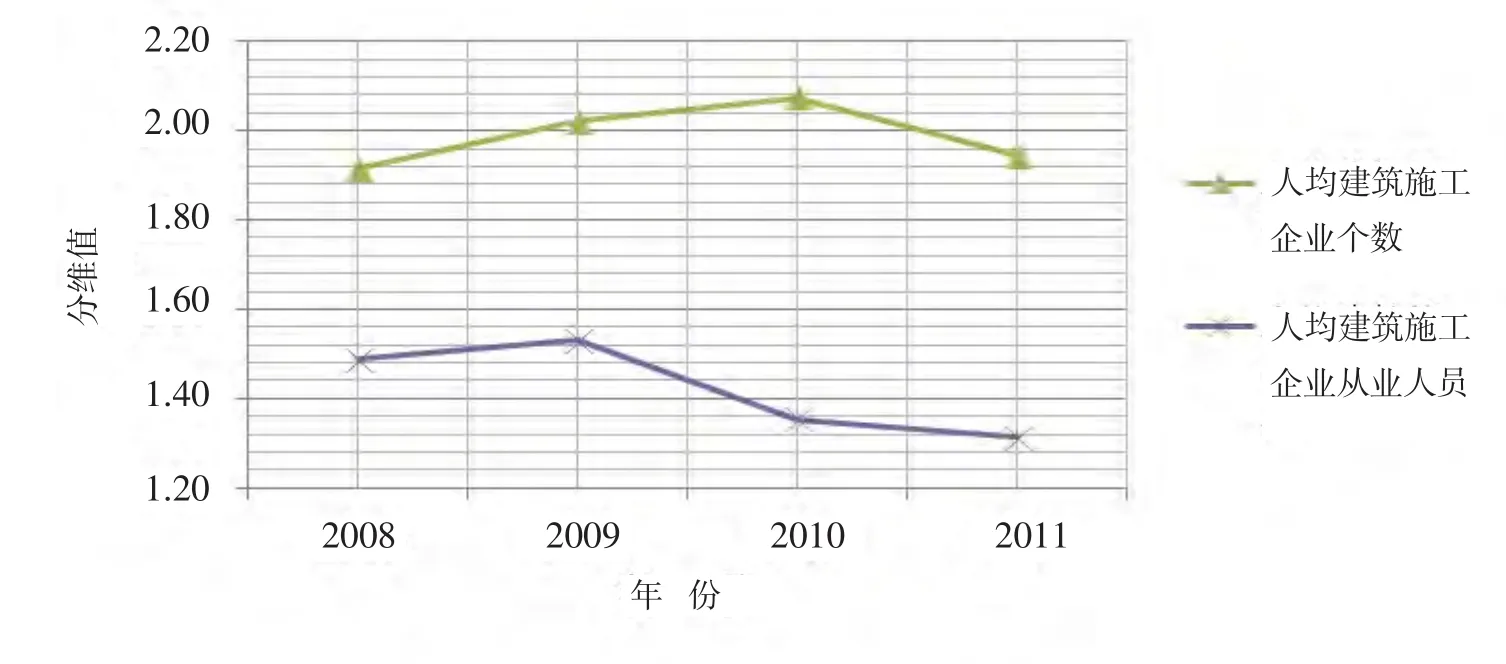
图3 2008-2011年北京市区县土地利用系统规模分维值变化图Fig.3 The change of fractal dimension value of the land sue system scale in Beijing’s districts and counties from 2008 to 2011

4 研究结论

本文以北京市为例，分别利用混沌理论和分形理论从时间序和空间序的角度揭示UTLU系统自组织演化的演化图景和结构复杂性问题.主要结论如下：

（1）以北京市为例，通过计算UTLU系统协同度时间序列的最大Lyapunov指数，判断系统是否存在混沌现象.结果表明，北京市的UTLU系统存在混沌现象.在此基础上，分析UTLU系统的初值敏感性、内在随机性、分岔、混沌吸引子、自相似等特性.

（2）以北京市为例，选取人均道路里程、人均道路面积、人均机动车保有量、人均公共停车设施、人均建筑施工企业个数和人均建筑施工企业从业人员数6个规模对象，利用位序—规模分析模型分别对UTLU系统中的交通系统和土地利用系统的演化结构进行评定，表明北京市区县UTLU系统规模差异处在变化中.

由于现阶段所收集的研究数据有限，本文所提出的方法只在北京市进行了应用分析，在今后的研究中，将选取其它城市进一步验证混沌理论和分形理论在UTLU系统中的适用性.

[1]孙胜阳,王江燕.轨道交通沿线土地利用分析及建议——以北京地铁1号线为例[J].交通运输系统工程与信息,2009,9(6):52-56.[SUN S Y,WANG J Y.Analy⁃sis and suggestions of land use patterns along rail transit corridor—a case study of Beijing metro line 1[J].Jour⁃nal of Transportation Systems Engineering and Informa⁃tion Technology,2009,9(6):52-56.]

[2]Debrezion G,Pels E,Rietveld P.The impact of rail trans⁃port on real estate prices an empirical analysis of the dutch housing market[J].Urban Studies,2011,48(5):997-1015.

[3]谢秉磊,丁川.TOD下城市轨道交通与土地利用的协调关系评价[J].交通运输系统工程与信息,2013,13(2):9-13.[XIE B L,DING C.An evaluation on coordi⁃nated relationship between urban rail transit and lan⁃duse under TOD mode[J].Journal of Transportation Sys⁃tems Engineering and Information Technology,2013,13(2):9-13.]

[4]Yigitcanlar T,Dur F.Developing a sustainability assess⁃ment model:the sustainable infrastructure,land-use,en⁃vironment and transport model[J].Sustainability,2010,2(1):321-340.

[5]应江黔.交通运输与土地利用综合模型的连续最优化方法[J].交通运输系统工程与信息,2007,7(3):64-72.[YING J Q.Continuous optimization method for inte⁃grated land use/transport models[J].Journal of Transpor⁃tation Systems Engineering and Information Technology,2007,7(3):64-72.]

[6]Kakaraparthi S K,Kockelman K M.Application of Ur⁃banSim to the Austin,Texas,Region:Integrated-model forecasts for the year 2030[J].Journal of Urban Planning and Development,2010,137(3):238-247.

[7]韩文秀,郁俊莉,王其文.我国资本市场混沌特性研究[J].系统工程理论与实践,2002,22(10):43-48.[HAN W X,YU J L,WANG Q W.A study on the chaotic char acteristics for the capital market[J].Systems Engineer ing-Theory&Practice,2002,22(10):43-48.]

[8]张海龙,闵富红,王恩荣.关于Lyapunov指数计算方法的比较[J].南京师范大学学报（工程技术版）,2012,12(1):5-9.[ZHANG H L,MIN H H,WANG E H.The comparison for lyapunov exponents calculation methods[J].Journal of Nanjing Normal University(Engineering and Technology Edition),2012,12(1):5-9.]

[9]苏宏志,陈永昌.混沌和分形理论揭示了建筑和城市演化的图景[J].新建筑,2008,(2):75-78.[SU H Z,CHEN Y C.Chaos theory and fractal theory post the evo⁃lution prospect of architecture and city[J].New Architec⁃ture,2008,(2):75-78.]

[10]才华.基于自组织理论的黑龙江省城市系统演化发展研究[D].哈尔滨工程大学,2006.[CAI H.Research on Heilongjiang city system evolvement and development based on self-organization theory[D].Harbin Engineer⁃ing University,2009.]

[11]苏策.城市游憩空间发展自组织研究——以武汉市为例[D].湖南师范大学,2009.[SU C.Research on self-organization of urban recreation space develop⁃ment—A case study of Wuhan[D].Hunan Normal Uni⁃versity,2009.]