中国股市和美国股市的联动性分析

曾 艳

（韶关学院 数学与信息科学学院，广东 韶关512005）

中美股市之间是否在一定程度上存在某种关系，存在什么样的联系，一直是投资界研究的热点.本文选取中美股市中具有代表性的指数建立VAR模型，运用脉冲响应函数和方差分解进行分析，试图找出中美股市的联动性.选取中国股市中影响较大的上证综合指数和深圳成分指数代表中国股市，美国股市则选取道琼斯工业平均指数和纳斯达克指数进行分析.本文采用上证综合指数、深圳成分指数、道琼斯工业平均指数（简称“道指”）、纳斯达克指数2008年4月14日至2011年4月1日的日收盘价作为样本数据.数据来源于锐思金融数据库.

1 中美股市的相关性分析

1.1 单位根检验

为了简化指数名称，用SHSP代表上证综合指数，SZSP代表深圳成分指数，DQSSP代表道琼斯工业平均指数，NSDSP代表纳斯达克指数，其对数差分分别表示为△LSHSP、△LSZSP、△LDQSSP、△LNSDSP.对各股票指数进行单位根检验，检验结果见表1.

表1 各指数的单位根检验

表2 各指数的对数差单位根检验

从表1和表2可以看出，各股票指数序列是非平稳的，但经过差分后的序列是平稳的，说明各股票指数是平稳序列.

1.2 Granger因果检验

表3和表4分别给出上证综合指数与深圳成分指数，以及道琼斯工业平均指数和纳斯达克指数的Granger因果检验.

表3 主要指数的Granger因果检验

从表3可以看出，在5%的显著水平下，上海股市是深圳股市股价波动的Granger原因，深圳股市也是上海股市股价波动的Granger原因；道琼斯工业平均指数是纳斯达克指数价格波动的Granger原因，纳斯达克指数也是道琼斯工业平均指数价格波动的原因.

1.3 脉冲响应函数

图1 SZSP的冲击引起SHSP的响应函数图

图2 SHSP的冲击引起SZSP的响应函数图

图1和图2给出了上证综合指数和深圳成分指数的脉冲响应函数图，从图1中可以看出，深圳股市股价波动的冲击对上海股市的股价影响较小，呈缓慢上升的趋势，而由图2可知，上海股市股价波动的冲击对深圳股市股价影响较大，在第1期达到最高点，随着期数的增加，缓慢下降，但总体影响较大.上海股市相比深圳股市而言，较为成熟，更具影响力，在分析中美股市方面，选取上证综合指数代表中国股市，较为合适.

图3和图4给出了道琼斯工业平均指数和纳斯达克指数的脉冲响应函数图.

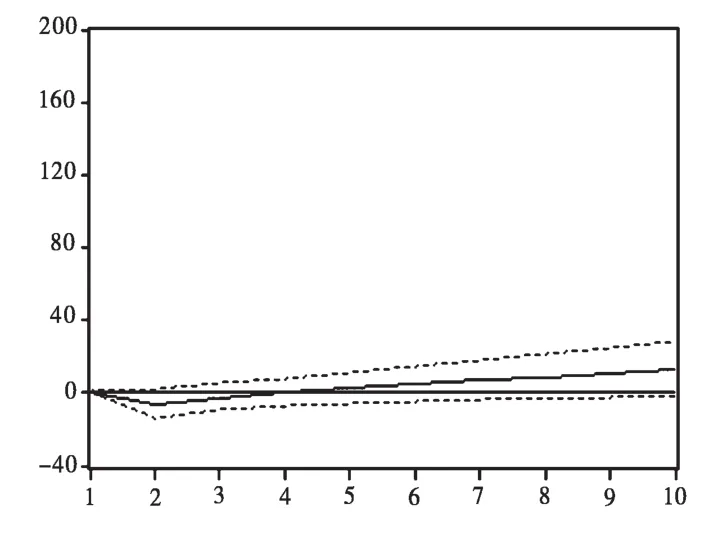
图3 NSDSP的冲击引起DQSSP的响应函数图

图4 DQSSP的冲击引起NSDSP的响应函数图

从图3中可以看出，纳斯达克指数价格波动的冲击对道琼斯工业平均指数影响较小，有正有负，始终在0周围波动.而由图4可知，道琼斯工业平均指数价格波动对纳斯达克指数冲击较大，在第1期迅速增大，达到最高点后，有所下降，从第4期后，冲击力度不变，趋于稳定.道琼斯工业平均指数相比纳斯达克指数而言，更具影响力，在分析中美股市方面，选取道琼斯工业平均指数代表美国股市，较为合适.

2.4 方差分解

图5～图8给出了各股票指数价格波动的方差贡献率，上证综合指数对深圳成分指数价格的波动达到85%以上，这说明上海股票市场在一定程度上影响着深圳股票市场，道琼斯工业平均指数对纳斯达克指数价格波动的方差贡献率先增加后趋于平稳，在45%左右.

图5 SHSP的方差分解

图6 SZSP的方差分解

图7 DQSSP的方差分解

图8 NSDSP的方差分解

2 中美股市的联动性分析

选取上证综合指数和深圳成分指数来对中美股市之间的相互进行分析，同样地，先对股票指数进行Granger因果检验，检验股票指数间存在因果关系，再建立VAR模型，进行脉冲响应函数分析以及方差分解.

2.1 Granger因果检验

对上证综合指数与道琼斯工业平均指数进行Granger因果检验，如表4所示.从表4中可以看出，在5%的显著水平下，美国股市是中国股市股价波动的Granger原因，而中国股市不是美国股市股价波动的Granger原因.

表4 SHHP和DQSSP的Granger因果检验

3.2 脉冲响应函数

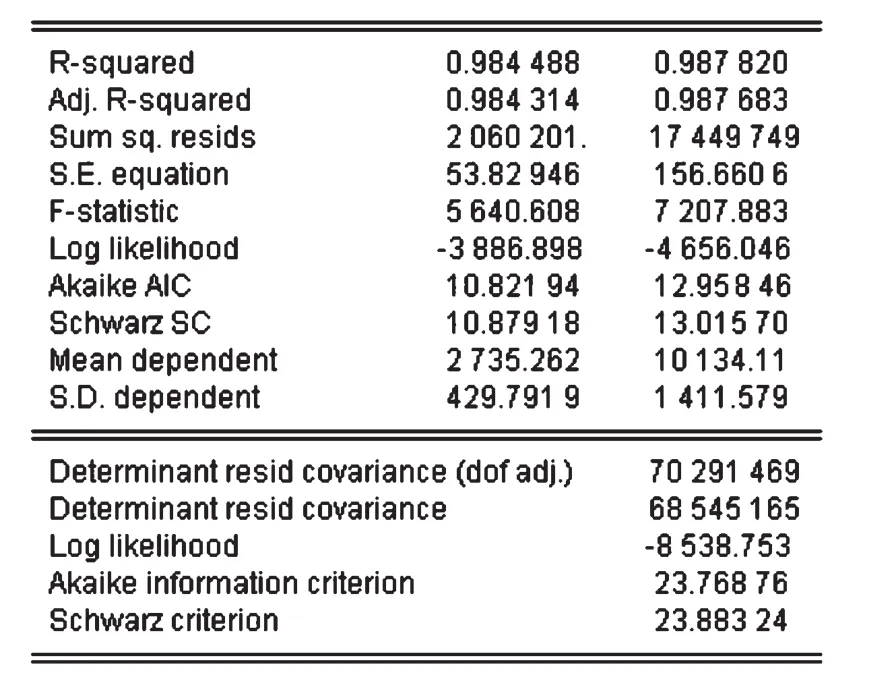
图9 VAR模型的拟合效果

通过建立VAR模型，研究中美股市的联动性，运用Eviews5.0软件，根据AIC准则和SC准则，确定了最优的滞后阶数q=4，由图9可知R2=0.98，说明模型的拟合效果较好.

根据各参数，得出VAR模型的具体表达式为：

接下来，进一步分析上证综合指数和道琼斯指数的脉冲响应函数.图10和图11给出了上证综合指数和道琼斯指数的脉冲响应函数.

图10 DQSP的冲击引起SHSP的响应函数

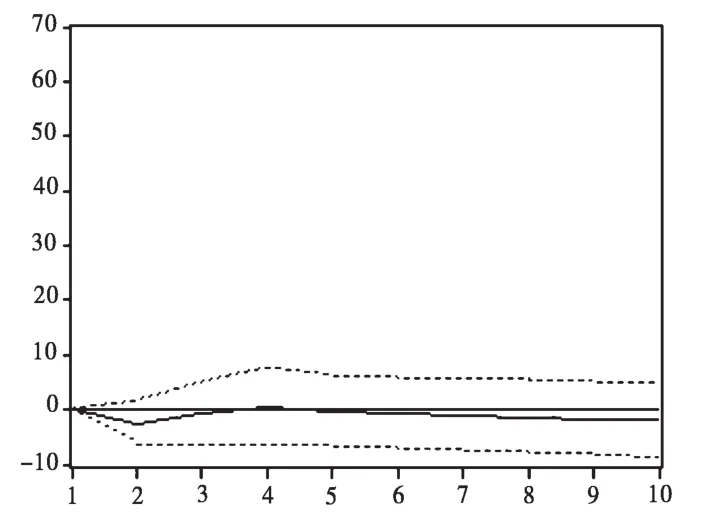
图11 SHSP的冲击引起DQSSP的响应函数图

从图10和图11可知，美国股市对中国股市的影响较大，而中国股市对美国股市的波动影响很小，在第1期时，有较小的影响，随后几乎没什么影响.因此，美国股市波动对中国股市有一定的影响，但中国股市波动对美国股市的影响较小，中美股市存在一定的联动性.

2.3 方差分解

图12和图13给出了上证综合指数和道琼斯工业平均指数的方差贡献率.

图12 SHSP的方差贡献

图13 DQSSP的方差贡献

同样的，美国股市波动对中国股市有一定的影响，但中国股市波动对美国股市的影响较小，中美股市存在一定的联动性.

［1］Connolly,Robert A,Wang F.On stock market return co-movement:macroeconomic ne-ws,dispersion of beliefs and contagion［D］.Carolina:University of North Carolina，2002.

［2］韩非,肖辉.中美股市间的联动性分析［J］.金融研究,2005(11):117-129.

［3］罗子光.香港股市与内地股市的联动性研究［J］.南方金融,2008(12):21-25.

［4］高铁梅.计量经济分析方法与建模Eviews应用及实例［M］.北京:清华大学出版社，2009:268-318.