基于Voronoi图的林分空间模型及分布格局研究

2014-05-14吴舒辞李建军王传立

生态学报 2014年6期

刘帅，吴舒辞，* ，王红，2，张江，李建军，王传立

(1.中南林业科技大学，长沙 410004;2.湖南省科学技术厅，长沙 410013)

与林木空间位置有关的林分结构统称为林分空间结构，主要包含树种混交、大小分化和空间格局3个方面的内容。林分空间结构决定了林木间的竞争优势及其空间生态位，在很大程度上影响着林分的健康和稳定。采用何种手段从而更加准确、有效地表征林分空间结构特征一直是现代森林经理学研究热点，对于近自然森林经营意义重大［1-2］。

林分空间格局源于种群空间格局，指林木在水平空间上的配置状况和分布特征，是林木生长特性、种内种间关系、环境因子等综合作用的结果［3］。研究林木空间格局有助于理解森林的建立、更新和发展过程，是实际营林所必须测定的空间结构因子。目前，林分空间格局研究多采用与距离有关的格局分析方法，主要包括聚集指数、精确最近邻体分析［4］、Ripley's K(d)函数分析［5］。其中，精确最近邻体分析和Ripley's K(d)函数分析以林木坐标点图为基础进行格局分析，亦称为点格局分析［4，6］，已被广泛应用于描述林木的空间分布，可分析不同距离尺度下的种群格局及不同种群的种间关联关系，具有显著的优越性。但该类方法提供的是种群的统计格局，很难从中导出与森林空间经营直接相关的具体信息，且方法复杂，计算量较大。惠刚盈［7-8］提出基于相邻木角度测量的角尺度，该方法简单可靠，既能分析林分整体空间格局，又可表征林分精细结构即林木点结构的分布格局，是林分经营中最常用的格局分析方法［2-3］。但角尺度与距离无关，无法反映林分疏密程度及相邻木距离等空间要素。

Voronoi图是计算几何的基本数据结构，按照对象集合元素的最近邻原则将空间划分为许多不相重叠的凸多边形(Voronoi多边形)。每个凸多边形都有唯一的集合元素与之相关联，其内任一点到该元素的距离总小于到其他元素的距离。Voronoi图具有邻接性、唯一性、空间动态等特性，适用于表征空间目标的复杂邻域关系［9］。由于可根据需要对Voronoi图定义进行扩展，Voronoi图在计算机图形学、分子生物学、空间规划等众多领域具有广阔的应用背景［10-11］。Brown［12］最早将 Voronoi图引入林学领域，提出林木竞争分析的 APA(area potentially available)指数;汤孟平等将Voronoi图用于群落优势树种的种内种间分析［13］和混交度研究［14］;赵春燕［15］等人通过 Voronoi图研究红树林空间结构指数。但应用Voronoi图深入分析林分空间结构特征及林木分布格局的研究尚不多见。本研究选择南洞庭湖龙虎山林场典型常绿阔叶林为对象，建立基于Voronoi图的林分空间模型，量化林木空间结构，包括林木水平位置、空间近邻关系、空间密度等信息。在该模型的基础上，分析样地林木整体空间格局及主要乔木种群的格局动态。

1 研究区概况和样地调查

研究地点位于南洞庭湖区龙虎山林场，地理位置为东经 112°17'2″—112°18'30″，北纬 28°54'4″—28°54'56″。该地属中亚热带季风湿润气候，年均气温16.7℃。林场内有木本植物100余种，其代表性林分是青椆混交林，主要乔木树种有青椆(Cyclobalanopsis myrsinaefolia)、香樟(Cinnamomum camphora)、青冈栎(Cyclobalanopsis glauca)、毛豹皮樟(Litsea coreana var.lanuginosa)、苦槠(Castanopsis sclerophylla)、钩栗 (Castanopsis tibetana)、马褂木(Liriodendron chinense)、木荷(Schima superba)、枫香(Liquidambar formosana)等。当地资料和林分调查表明，研究地森林群落是受过轻微干扰而形成的天然次生林，青椆、香樟、青冈栎等为当地优势树种［16-17］。

笔者于2010年8月在研究区内设置面积为100m×100m的标准样地1块。采用全站仪等设备对样地内胸径大于5cm的活立木进行定位、编号及每木检尺，检测内容为林木位置、树种信息、胸径、树高、冠幅等。以样地西南角为坐标原点，记样地内林木的相对空间坐标为(x，y)，其中x表示东西方向坐标，y表示南北方向坐标。该次研究共涉及林木982株。

2 研究方法

2.1 Voronoi图定义

设二维平面空间中有一离散点集P={p1，p2，…，pn}，其中任意两点不相等，任意四点不共圆。点集中任一元素pi(1≤i≤n)根据空间邻接关系确定Voronoi多边形 tpi(1 ≤ i≤ n)［10］:

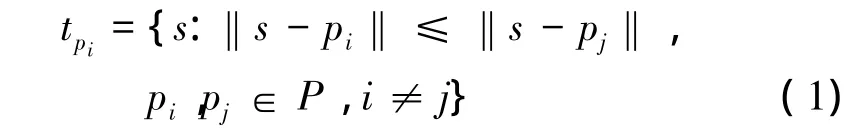
式中，符号‖·‖表示两点间的欧氏距离，点pi称为Voronoi多边形tpi的生成元，该定义确保Voronoi多边形tpi内任意点s到生成元pi的距离小于到其他生成元pj的距离，则由tpi(1≤i≤n)组合成的平面图形称为离散点集P的Voronoi图。至此，离散点集完成对二维平面的空间剖分。

2.2 基于Voronoi图的格局分析方法

离散点集在平面空间通常有3种格局分布形式:均匀分布、随机分布和聚集分布，如图1所示。点集的Voronoi图可以直观地反映点状目标在平面空间的分布情况［18］。当平面点均匀分布时，相邻Voronoi多边形大小相当;聚集分布时，Voronoi多边形大小各异，聚集区内的较小，聚集区外的较大;随机分布时的情况则介于均匀分布和聚集分布之间。可见，通过量化Voronoi多边形面积的变化关系则可确定平面点的分布格局。因此，本研究引入变异系数(Coefficient of Variation，CV)来衡量Voronoi多边形面积的相对变化，其表达式为:

式中，σ是n个彼此邻接的Voronoi多边形面积的标准差，¯s是其面积均值，xi表示第i个Voronoi多边形的面积，¯xi表示第i个Voronoi多边形及其相邻Voronoi多边形面积的均值。按照公式(2)计算图1的Voronoi图的变异系数，结果依次为:0.125、0.273、0.781。

图1 点集的空间分布Fig.1 Spatial distribution of point set

变异系数反映了单位均值上点状目标的离散程度和分布状态，当取值从低到高时，空间点将依次经历均匀、随机、聚集3种分布格局。为明确3种不同分布格局下变异系数的取值范围，采用Monter Carlo模拟方法对平面点的分布进行显著性检测，具体步骤如下:模拟本研究林分样地在100m×100m的二维平面随机布点982个，根据点位置对二维平面进行Voronoi分割，计算每个Voronoi多边形的面积;为研究格局分布与空间尺度的关系，采用种-面积关系研究中的巢式取样［23］，始终以坐标原点(西南角)为起点，取样尺度按每次4m递增，一共获取25个方形小样地:4m×4m，8m×8m，12m×12m，…，100m×100m，计算每个小样地内Voronoi多边形的变异系数，以上过程重复99次，按99%的置信水平来确定置信区间。再根据样地林木实际分布情况计算变异系数，计算结果如果在置信区间内，则为随机分布;如果在置信区间外，则显著偏离随机分布。以上计算过程在MATLAB 7.1平台上完成。

2.3 边缘校正

受人为划分样地的影响，样地边缘林木的相邻木可能位于样地以外，因而样地边缘木的Voronoi多边形是不完整的。计算这部分林木的变异系数，会使整体结果产生较大误差，进而影响林木空间格局判断的精度。

传统的边缘校正方法，如设置8邻域样地［19］、建立缓冲区［20］等不适用本研究。本研究的处理办法是标记所有以样地边界为边的Voronoi多边形，在林木空间格局分析时不纳入变异系数的计算中。

3 结果与分析

3.1 林分空间Voronoi图模型

点格局分析将林木的空间位置视为平面点，从点的数量特征入手分析其空间格局［6］。然而，实际情况是森林中每株林木都要通过与周边林木竞争来获取必要的资源和生长空间，仅仅将林木抽象成平面点会引起林木空间信息的缺失。因此，本研究建立样地林木水平空间的Voronoi图模型，借此反映林木及其“影响圈”的空间分布，作为进一步分析林木空间格局的基础。

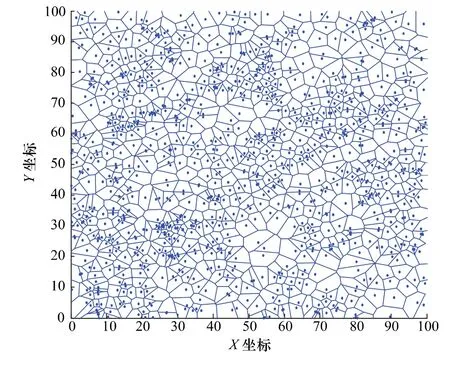
图2 样地林木空间分布Voronoi图Fig.2 Voronoi diagram of spatial distribution in sample plot

为了建模需要，忽略样地的地形、地貌特征，视其为二维平面，样地内所有起径5cm以上的林木为该二维平面的点状目标，在MATLAB平台上编程绘制样地林木Voronoi图并计算其相关参数，结果如图2所示。该Voronoi图模型不但显示了林木详细的空间位置，可用于定性分析林木空间格局，还能通过该图提取林分空间结构信息，具体如下:

(1)平面点即生成元代表林木在样地中的空间相对位置 (xi，yi)，1≤ i≤ 982。

(2)Voronoi多边形代表林木的“影响圈”，即林木所占据的空间生态位，反映了林木间相互作用及对环境适应的结果，其面积或周长度量了该空间的大小，其面积的倒数则表示该林木的点密度。一定范围内Voronoi多边形平均面积¯s的倒数则表示该区域内林木的空间密度ρ，即:

(3)林木的生长状况、分布格局等情况与其直接邻体的数量、规模、距离有密切关系。两株林木相邻的依据是两者对应的Voronoi多边形共享一条边，该边称为公共边。对于非样地边缘林木，其Voronoi多边形公共边的条数代表了该林木的相邻木数目。

(4)Voronoi图具有唯一的对偶结构Delaunay三角网，如图3所示，实线代表Delaunay三角网，虚线表示相对应的Voronoi图。单个Delaunay三角形包含相邻木间的距离信息和角度信息，其边长长度等于参照树与其相邻木的距离，其内角可直接计算参照树的角尺度［7］。

经样地边缘校正，本研究样地林木Voronoi图的有关参数及取值如表1所示。

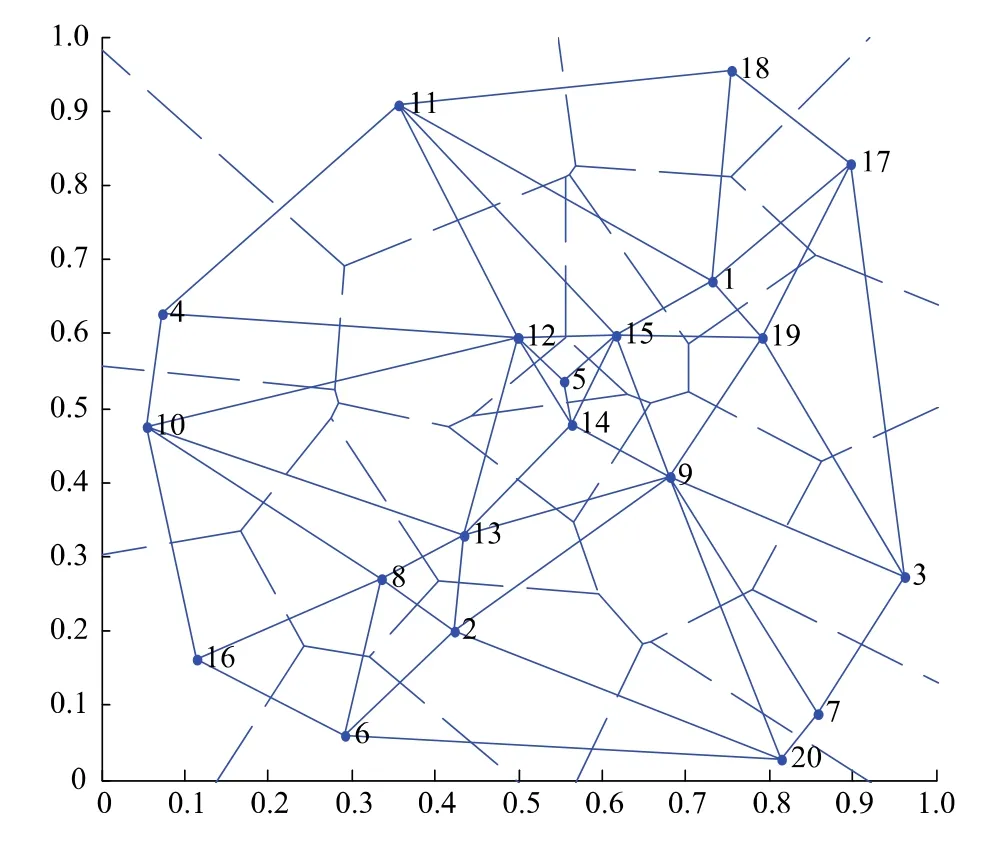
图3 Delaunay三角网示例Fig.3 An example of Delaunay Triangulation

3.2 林木空间格局分析

3.2.1 林分整体分布格局

本文采用基于Voronoi图变异系数的格局分析方法研究不同空间尺度下的林木分布格局，结果如图4所示。当小尺度取样时，空间格局呈显著聚集分布，20—40m为强度聚集，观察图2可看到该尺度下有明显的林木聚生区域。此后，随着尺度的增大，变异系数逐渐减小并趋于稳定。当取样尺度大于76m时，空间格局呈接近随机分布的轻度聚集，说明在大尺度范围林木的空间格局有从聚集分布向随机分布过渡的趋势。由此可知，基于Voronoi多边形变异系数的格局分析与取样尺度有密切关系，尺度越大所包含样本越多，则分析结果越接近林分真实的空间格局。

表1 样地Voronoi图信息Table 1 Information of Voronoi diagram in the plot

为对比基于Voronoi图的格局分析方法，本研究选取结构化森林经营中有代表性的角尺度［7-8］方法分析同一块样地的空间格局。图4为样地中角尺度各个取值的统计情况，其均值为0.532，表明样地林木整体上呈轻度聚集分布。可见，基于Voronoi图变异系数方法与角尺度方法对于林分整体空间格局的判断是一致的。图4显示了25种不同空间尺度下变异系数和角尺度的相关性分析结果，其相关系数R2等于0.7714(显著正相关)，则进一步说明两种格局分析方法可以相互替代。

图4 林分空间分布格局Fig.4 Stand spatial pattern

3.2.2 主要树种的空间格局动态

林木分布格局不仅可以定量描述林分的水平空间结构，而且能够说明林分种群的动态变化。目前多以林木径级结构代替年龄结构分析种群格局动态［21］。本研究按照胡小兵等人［22］对木本植物种群的划分标准，以胸径10cm为界将样地林木分为小径木(小树和中树，胸径小于等于10cm)和大径木(大树，胸径大于10cm)，分析林分内主要树种的空间格局动态(图5)，图中横坐标表示取样尺度，纵坐标对应具体树种的Voronoi图变异系数值。

图5 主要树种的空间分布格局Fig.5 Spatial pattern of main tree species

青椆属地带性常绿阔叶优势树种，具有水源涵养和水土保持作用，更新能力强，兼有实生和萌生两种繁殖方式，其小径木呈强度聚集，且随尺度增大聚集程度进一步加深。由于在群落中分布最广，数量最多，该树种所承受的竞争压力也最大，因而其大径木虽呈显著聚集，但聚集程度相比小径木明显降低(图5)。香樟是群落中另一种优势树种，根系发达，具有较强的适应性，其种子轻，结实量大，散播范围广，在群落中与青椆全方位竞争，小树在林分内呈轻度聚集分布，而成年大树则因自然稀疏其格局过渡到随机分布(图5)。青冈栎与青椆同属山毛榉科，林下更新良好，种子粒大而重，萌发率高，小树多聚生在一起。但青冈栎在群落中的优势地位不及青椆和香樟，由于自稀疏及环境影响，使得其成年大树的空间格局在随机与聚集分布之间震荡(图5)。毛豹皮樟是群落中的非优势种(限于篇幅，非优势种仅列出毛豹皮樟)，其空间格局波动较大，分布特征不明显，这可能与该种群数量较少有关(图5)。总的来看，样地内小径木的空间格局多为聚集分布，大径木主要呈轻度聚集或随机分布;优势种空间分布较明显，非优势种分布特征不明显或呈随机分布;林分空间格局主要由优势种的格局决定，各树种分布格局的动态变化与林分整体呈聚集态，且有向随机分布演变的趋势保持一致。

以上分析表明，受随机自稀疏、个体生长差异等多重因素影响，同一树种在不同的发育阶段，其空间格局会发生动态变化。同时，受空间尺度改变的影响，林木在小尺度上形成的分布格局可能会在大尺度上复合进而引起分布状态的改变，使得种群分布动态表现出强烈的空间及时间特征。

4 结论与讨论

本研究以南洞庭湖龙虎山林场典型常绿阔叶林群落为研究对象，根据林木点位置剖分样地平面空间，建立基于Voronoi图的林分空间模型。该模型不但能显示出林木的空间位置和疏密程度，而且量化了林木的空间邻近关系，具有明确的林学及生态学意义。对于以参照树为中心的空间结构单元，其相邻木可以由参照树的Voronoi多边形公共边唯一确定，解决了长期以来相邻木选取尺度模糊的问题。

本研究提出基于Voronoi图的格局分析方法，应用该方法分析林分的整体空间格局。与角尺度方法的对比研究显示，Voronoi图变异系数和角尺度存在显著的正相关关系，表明基于Voronoi图的格局分析方法同样能有效刻画林木空间分布特征。进一步使用该方法从不同的时空尺度上描述了林分主要树种的空间格局动态，并结合林木生长特性阐释了格局动态变化的原因:在时间尺度上，林木的自然稀疏是引起种群格局动态的主要原因;在空间尺度上，自然稀疏的作用范围会因尺度的改变而相应改变，使得小尺度上形成的格局会因尺度增大而复合成更大规模的格局分布，从而改变种群格局面貌。

研究林木空间关系的最终目的是采取合理的经营措施调控林分空间结构，而具体的营林效果可通过经营前后的林分Voronoi图体现出来。例如，择伐部分林木后，原本由被伐林木所占据的空间单元并入周边邻木，由此引发的空间格局变化可从林木Voronoi图变异系数上反映出来。对于整体呈聚集分布的林分，其中必然存在某些林木聚集区域和稀疏区域，根据林分Voronoi图的空间密度信息可以找出这些待调控区域并施加不同的经营措施(择伐或补植)。因此，本研究结果对于天然林空间结构重构及调控具有一定指导意义。

通过相邻木连线的垂直平分线来构造Voronoi图，所隐含的林学假设是彼此相邻的两株林木处在同等竞争地位，然而实际情况中这些林木多为不对称竞争状态。胸径粗大、根系发达的林木将处于优势地位，占据更多的资源及生存空间。为使所建模型能反映林分真实情况，后续研究可将胸径、冠幅等林木属性作为权值建立林分加权Voronoi图，给林木空间单元划分提供更多科学依据。

此外，还可深入挖掘森林的空间结构信息，建立更为完善的空间模型。例如，考虑林木对光能的利用，可引入树高因子，对林分三维空间进行Voronoi剖分;结合GIS等先进技术，建立更大研究尺度、多层次的森林空间模型。

［1］Shan Y，Bettinger P，Cieszewski C J，Li R T.Trends in spatial forest planning.Mathematical and Computational Forestry＆Natural Resource Sciences，2009，1(2):86-112.

［2］Tang M P.Advances in study of forest spatial structure.Scientia Silvae Sinicae，2010，46(1):117-122.

［3］Zhang H R，Tang S Z.Research of the Northeast Natural Forest Sustainable Management Technology.Beijing:China Forestry Publishing House，2011:81-82.

［4］Moeur M.Characterizing spatial patterns of trees using stemmapped data.Forest Science，1993，39(4):756-775.

［5］Ripley B D.Modelling spatial patterns.Journal of Royal Statistical Society.Series B，1977，39(2):172-212.

［6］Zhang J T.Analysis of spatial point pattern for plant species.Acta Phytoecologica Sinica，1998，22(4):344-349.

［7］Hui G Y，Von Gadow K，Alert M.The neighbourhood pattern-a new structure parameter for describing distribution of forest tree position.Scientia Silvae Sinicae，1999，35(1):37-42.

［8］Hui G Y，Von Gadow K，Hu Y B，Chen B W.Characterizing forest spatial distribution pattern with the mean value of uniform angle index.Acta Ecologica Sinica，2004，24(6):1225-1229.

［9］Charles D，Gilles G.Voronoi tessellation to study the numerical density and the spatial distribution of neurones.Journal of Chemical Neuroanatomy，2000，20(1):83-92.

［10］Skare Ø，Møller J，Jensen E B V.Bayesian analysis of spatial point processesin the neighbourhood ofVoronoinetworks.Statistics and Computing，2007，17(4):369-379.

［11］Kristensen L，Olsen J，Weiner J，Griepentrog H W，Nørremark M.Describing the spatial pattern of crop plants with special reference to crop-weed competition studies.Field Crops Research，2006，96(2/3):207-215.

［12］Brown G S.Point density in stems per acre.New Zealand Forestry Service Research Notes，1965，38:1-11.

［13］Tang M P，Chen Y G，Shi Y J，Zhou G M，Zhao M S.Intraspecific and interspecific competition analysis of community dominant plant populations based on Voronoi diagram.Acta Ecologica sinica，2007，27(11):4707-4716.

［14］Tang M P，Zhou G M，Chen Y G，et al.Mingling of evergreen broad-leaved forests in Tianmu mountain based on Voronoi diagram.Scientia Silvae Sinicae，2009，45(6):1-5.

［15］Zhao C Y，Li J P，Li J J.Quantitative analysis of forest stand spatialstructure based on Voronoidiagram and Delaunay triangulated network.Scientia Silvae Sinicae，2010，46(6):78-84.

［16］Lü Y，Zhang H，Wang X Y，Deng Z A，Li J J.Storey structure study of Cyclobalanopsis myrsinaefolia mixed stand based on storey index.Forest Resources Management，2012，(3):81-84.

［17］Li J J，Zhang H R，Wang C L，Zang H，Cao X P.Discussion on spatial optimization modelling of water resource conservation forests and management practice of forest functions.Journal of Central South University of Forestry and Technology，2012，32(3):23-28.

［18］Qin X W，Zhang S Q，Li X F，Na X D，Liu C Y.Spatial pattern of red-crowned crane nest-sites based on Voronoi diagram.Chinese Journal of Ecology，2008，27(12):2118-2122.

［19］Haase P.Spatial pattern analysis in ecology based on Ripley’s K-function:Introduction and methods of edge correction.Journal of Vegetation Science，1995，6(4):575-582.

［20］HuiG Y， Gadow K， HuY B.Structure-BasedForest Management.Beijing:China Forestry Publishing House，2007:153-154.

［21］Zhang H R，Tang M P，Shu Q T.Theory and Practice of Forest Ecological Harvesting.Beijing:Publishing House ofChina Forestry，2006:225-226.

［22］Hu X B，Yu M J.Size structure and distribution pattern of Cyclobalanopsisglauca population in evergreen broad-leaved forests.Journal of Zhejiang University:Science Edition，2003，30(5):574-579.

［23］Tang Z Y，Qiao X J，Fang J Y.Species-area relationship in biological communities.Biodiversity Science，2009，17(6):549-559.

参考文献

［2］汤孟平.森林空间结构研究现状与发展趋势.林业科学，2010，46(1):117-122.

［3］张会儒，唐守正.东北天然林可持续经营技术研究.北京:中国林业出版社，2011:81-82.

［6］张金屯.植物种群空间分布的点格局分析.植物生态学报，1998，22(4):344-349.

［7］惠刚盈，Von Gadow K，Alert M.角尺度——一个描述林木个体分布格局的结构参数.林业科学，1999，35(1):37-42.

［8］惠刚盈，Gadow K V，胡艳波，陈伯望.林木分布格局类型的角尺度均值分析方法.生态学报，2004，24(6):1225-1229.

［13］汤孟平，陈永刚，施拥军，周国模，赵明水.基于Voronoi图的群落优势树种种内种间竞争.生态学报，2007，27(11):4707-4716.

［14］汤孟平，周国模，陈永刚，，赵明水，何一波.基于Voronoi图的天目山常绿阔叶林混交度.林业科学，2009，45(6):1-5.

［15］赵春燕，李际平，李建军.基于Voronoi图和Delaunay三角网的林分空间结构量化分析.林业科学，2010，46(6):78-84.

［16］吕勇，臧颢，万献军，邓志昂，李建军.基于林层指数的青椆混交林林层结构研究.林业资源管理，2012，(3):81-84.

［17］李建军，张会儒，王传立，臧颢，曹旭鹏.水源涵养林多功能经营结构优化模型初探.中南林业科技大学学报，2012，32(3):23-28.