量子拉比模型中的对称性与对称性破缺研究
2014-05-13王琼,冷洋
王 琼, 冷 洋
量子拉比模型中的对称性与对称性破缺研究
王 琼*1, 冷 洋2
(1. 湖南文理学院 物理与电子科学学院, 湖南 常德, 415000; 2. 三一重工 智能研究院, 湖南 长沙, 410100)
量子拉比模型(QRM)是描述物质与光相互作用最简单的模型之一. 本文发现在存在对称性的拉比模型中, 偏置的引入将破坏模型的对称性, 系统出现标度行为; 通过引入一个新的伊辛相互作用, 模型的对称性将重新修复. 发现这种对称性与对称性破缺规律性的结论在N态量子拉比模型同样存在.
量子拉比模型; 对称性; 对称性破缺
量子拉比模型(QRM)[1]在20世纪30年代已被大家所了解,是量子力学最简单和最典型的模型之一. 它描述的是一个二能级原子与单模玻色场间的相互作用,即所谓的单模耗散两能级系统. 拉比模型在离子阱[2]、电路量子电动力学[3—5]以及光子系统[6]等领域都有广泛的应用. 近些年来, 人们在寻找QRM封闭形式的解析解做了许多工作[7—13]. 但相比于JC模型, 由于QRM中存在反旋波项, 这样使得QRM中量子激发数不再是一个守恒量, 但从对称性角度考虑, 我们仍然可以将QRM当成是一个可积分系统[10]. 由于这个原因, Casanova等发现在二态QRM中存在一个无限维不变量子子空间[14], 并被Albert等推广到N态QRM[15]. 然而, 当对QRM引入偏置场后, 情况将完全不一样. 我们将引入偏置后的QRM称为偏置拉比模型(BRM), 可以用以下的Hamiltonian来描述:
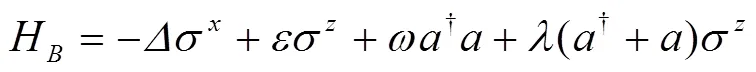
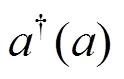
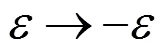
1 对称性与对称性破缺
在BRM引入一个新的自旋, 系统的Hamiltonian可以写为:
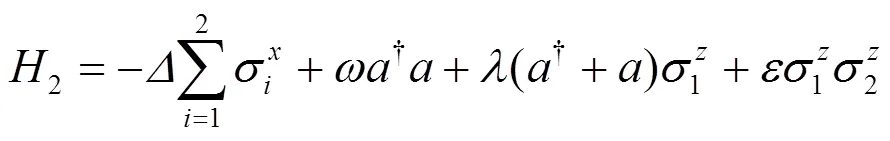
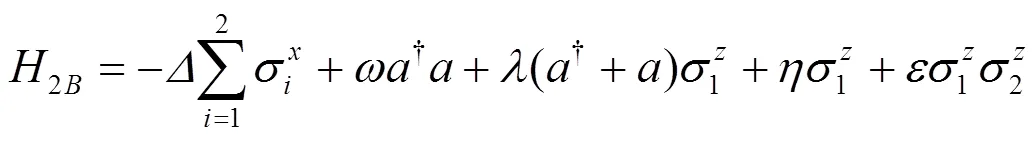

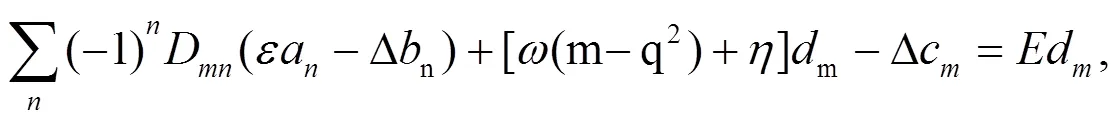
这里是本征能量,D为:
2 标度行为
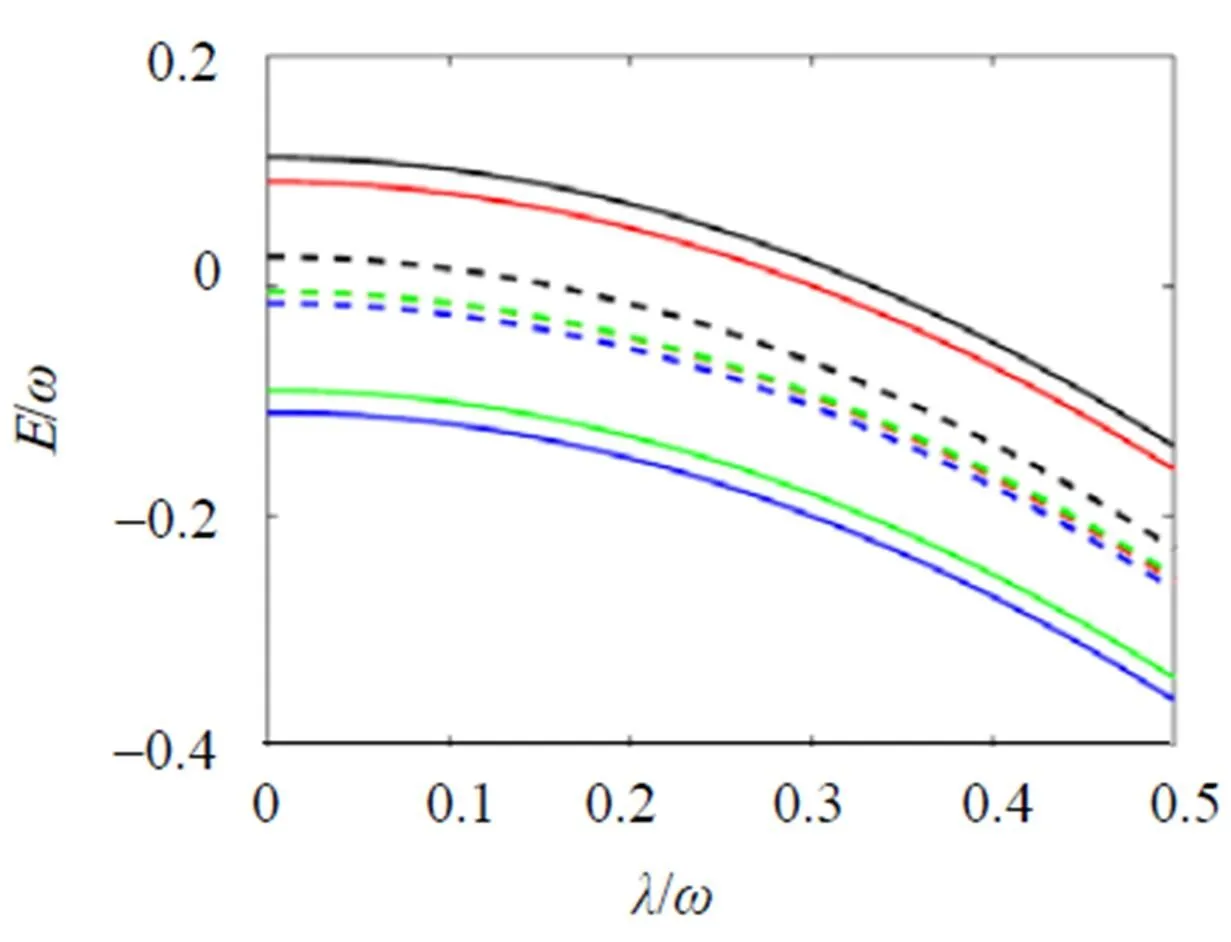
图1 H2(虚线, η = 0)以及H2B (实线, η≠ 0)的四个最低本征能级随拉比耦合强度λ的函数, 参数取值.
由基态波函数, 我们计算得到:
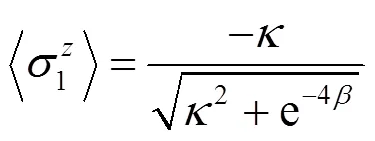
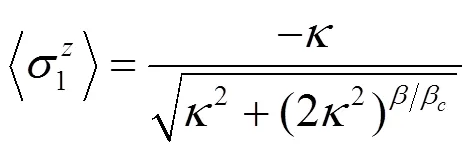
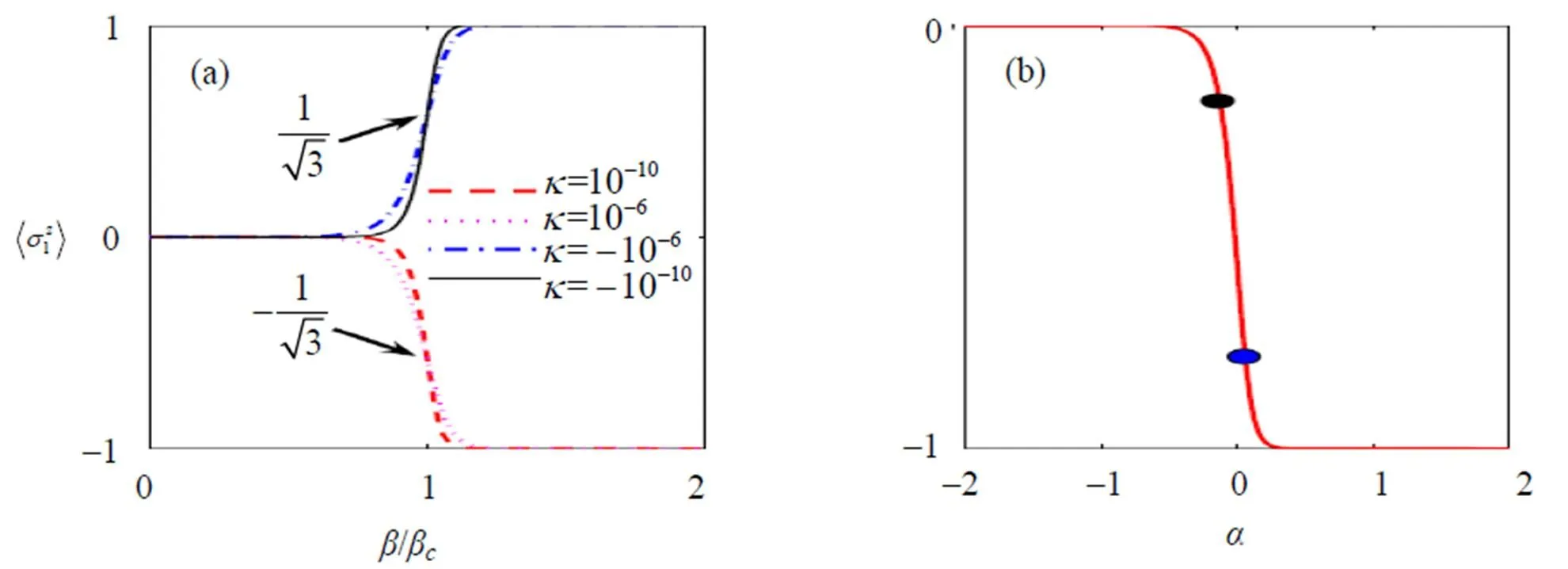
图2 本证基态下的标度行为. (a) 随变化, 表现两种不同的行为取决于与的差. (b)随变化, 对变现为标度不变性, 这里. 黑色圆点对应参数取值, . 黑色圆点对应参数取值, .
我们得出的对称性与对称性破缺规律性的结论在N态量子拉比模型同样成立. 考虑一个N态系统, 且第一个自旋与单模玻色场存在拉比相互作用, 同剩下N-1自旋存在伊辛相互作用, 系统的Hamilto- nian可以写为:
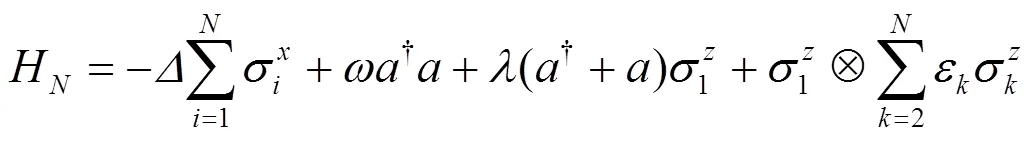
3 结论
我们研究了量子拉比模型中的对称性与对称性破缺问题. 发现存在对称性的拉比模型中, 偏置的引入将破坏模型的对称性, 系统出现标度行为; 通过引入一个新的伊辛相互作用, 模型的对称性将重新修复, 并且这种规律性的结论能推广到N态情形.
[1] Rabi I I. On the process of space quantization [J]. Phys Rev, 1936, 49: 324—328 .
[2] Leibfried D, Blatt R, Monroe C, et al. Quantum dynamics of single trapped ions [J]. Rev Mod Phys, 2003,75:281—320.
[3] Englund D, Faraon A, Fushman I, et al. Controlling cavity reflectivity with a single quantum dot [J]. Nature(London), 2007, 450: 857—861.
[4] Niemczyk T. Circuit quantum electrodynamics in the ultrastrong-coupling regime [J]. Nat Phys, 2010, 6: 772—776.
[5] P Forn-Dıaz. Observation of the Bloch-Siegert Shift in a Qubit-Oscillator System in the Ultrastrong Coupling Regime [J]. Phys Rev Lett, 2010, 105: 237001.
[6] Crespi A, Longhi S, Osellame R. Photonic Realization of the Quantum Rabi Model [J]. Phys Rev Lett, 2012, 108: 163601.
[7] Liu T, Wang K L, Feng M. Photonic Realization of the Quantum Rabi Model [J]. J Phys B, 2007, 40: 1967—1974.
[8] Irish E K. Generalized Rotating-Wave Approximation for Arbitrarily Large Coupling [J]. Phys Rev Lett, 2007, 99: 173601.
[9] Liu T, Wang K L, Feng. The generalized analytical approximation to the solution of the single-mode spin-boson model without rotating-wave approximation [J]. Europhys Lett, 2009, 86: 54003.
[10] Braak D. Integrability of the Rabi Model [J]. Phys Rev Lett, 2011, 107: 100401.
[11] Yu L, Zhu S, Liang Q, Chen G, Jia S. Analytical solutions for the Rabi model [J]. Phys Rev A, 2012, 86: 015803.
[12] Wolf F A, Kollar M, Braak D. Exact real-time dynamics of the quantum Rabi model [J]. Phys Rev A, 2012, 85: 053817.
[13] Chen Q H, Wang C, He S, Liu T, Wang K L. Exact solvability of the quantum Rabi model using Bogoliubov operators [J]. Phys Rev A, 2012,86:023822.
[14] Casanova J, et al. Deep Strong Coupling Regime of the Jaynes-Cummings Model [J]. Phys Rev Lett, 2010, 105: 263603.
[15] Albert V V. Quantum Rabi Model for N-State Atoms [J]. Phys Rev Lett, 2012, 108: 18040.
[16] Liu T, Feng M, Yang W L, Zou J H, Li L, Fan Y X, Wang K L. Parity breaking and scaling behavior in light-matter interaction [J]. Phys Rev A, 2013, 88: 013820.
[17] Gardas B, Dajka J. New symmetry in the Rabi model [J]. J Phys A, 2013, 46: 265302(2013).
Parity symmetry and parity breaking in the quantum Rabi model
WANG Qiong1, LEN Yang2
(1. College of Physics and Electronics, Hunan University of Arts and Science, Changde 415000, China; 2. Institute of Intelligence Research, Sany Heavy Industry, Changsha 410100, China)
The well-known quantum Rabi model strictly describes the simplest interaction between matter and the quantum light. We explore the possibility to generate new parity symmetry in the quantum Rabi model after a bias is introduced. We consider a physically realistic method by involving an additional spin into the quantum Rabi model to couple with the original spin by an Ising interaction. The rule can be found that the parity symmetry is broken by introducing a bias and then restored by adding new degrees of freedom.
quantum Rabi model; parity symmetry; parity breaking
O 413.2
1672-6146(2014)02-0018-04
10.3969/j.issn.1672-6146.2014.02.004
通讯作者email: zuiguiyixiu@163.com.
2014-05-04
国家自然科学基金专项基金(11347142); 光电信息集成与光学制造技术湖南省重点实验室; 湖南文理学院重点学科建设项目(光学).
(责任校对:谭长贵)
