多缝夫琅禾费衍射实验的计算机仿真

邓 磊, 汤剑锋



多缝夫琅禾费衍射实验的计算机仿真

邓 磊, 汤剑锋*

(湖南农业大学 理学院, 湖南 长沙, 410128)

为了更好解释多缝夫琅禾费衍射的实质, 利用Maple软件编程实现了对多缝夫琅禾费衍射的计算机仿真. 绘制出其相应的衍射图样和光强分布曲线, 通过改变可调参数详细分析了多缝夫琅禾费衍射的光强分布特点和缺级现象的影响因素. 研究结果表明仿真实验与实际实验结果一致, 程序简单, 仿真效果直观形象, 方便教学应用.

多缝夫琅禾费衍射; 缺级; 惠更斯-菲涅耳原理; Maple软件

光栅是现代科学研究和工程技术中进行光谱分析的重要工具. 在光栅衍射的理论研究和教学过程中, 研究多缝夫琅禾费衍射的光学图像及其与实验参数的关系十分重要. 由于目前很多教学过程中只简单采用了文本投影式或手绘图教学, 对光学现象缺乏精确、形象和动态的描述, 因此, 在课程讲授中主要依靠教师与学生的理解和想象, 给教学带来一系列困难.如果能用计算机根据实验参数适时仿真演示并生成光学图像, 提供学生观察光学现象的机会, 则可提高学生学习兴趣, 增强学生对光学规律的正确理解, 培养学生思维水平和创新能力, 达到事半功倍的效果[1—3].

根据惠更斯-菲涅耳原理[4], 多缝夫琅禾费衍射图样是单缝夫琅禾费衍射和各狭缝发出光束的干涉的合成结果. 所有狭缝独自产生的单缝衍射图样在屏幕上的位置相同, 形成彼此重叠的多幅单缝衍射图样. 但由于处在同一波面上的各狭缝发出的衍射光都是相干光, 在屏幕上会聚时会发生干涉[5]. 因此, 上述重叠的多幅单缝衍射图样中的光强就同时被相干叠加了, 导致了光强的重新分布, 呈现新的分布特点. 本文直接从惠更斯-菲涅耳原理出发, 运用Maple的数值计算和图形可视化功能[6], 主要讨论多缝夫琅禾费衍射的光强分布特点, 并绘制其光强分布曲线, 分析其缺级现象的成因及影响因素.

1 单缝夫琅禾费衍射的光强分布

如图1所示, 设单缝的缝宽为, 单缝的方向垂直纸面, 单缝与屏幕的间离为. 以垂直于单缝方向为轴, 屏幕上对称中心点为轴的坐标原点, 屏幕上任一点的坐标为x. 当一波长为的平行光束垂直于缝所在平面入射时, 其波阵面与缝平面平行, 缝上的各点都是相干的子波波源. 根据惠更斯原理, 将缝分为个平行于缝方向的等宽窄带次光源, 最下端的窄带为记为第1个, 依次向上分别记为第2, …,, …,个. 则第个窄带次光源的位置坐标可记为:

其中= 1, 2, …,. 从第个窄带次光源发出的次级子波到光屏上x处的光程为:

根据惠更斯-菲涅耳原理, 屏幕上任一点x处的光振动是来自个窄带次级子波的相干叠加, 可得屏幕上x处的复振幅和相对光强分别为[7]:

. (4)

2 多缝夫琅禾费衍射的光强分布

设透光缝数为, 缝宽为, 缝间不透光部分的宽度为, 则相邻透光缝上对应点之间的距离为=+, 多缝衍射屏与屏幕的距离为. 多缝衍射与单缝衍射的最大区别在于多缝之间存在干涉, 多缝衍射是各缝的单缝衍射和缝间衍射光相干叠加的综合结果.

由式(3)可得第个缝发射到屏幕上x处的衍射光的复振幅为:

屏幕上x处的总衍射效果是个缝的衍射光在该处的相干叠加, 计算可得多缝衍射的相对光强分布为:

式(6)中,

3 基于Maple的计算机仿真

3.1 多缝夫琅禾费衍射图样的形成分析

根据式(4)和式(6), 用Maple 13软件编写程序, 其中多缝夫琅禾费衍射仿真源程序见附录1. 设多缝屏与屏幕的距离取为固定值= 1 000 mm, 实验参数= 5,= 0.003 mm,= 0.009 mm,= 432.8 nm. 首先, 只考虑各狭缝中出射光线相互间的干涉效果(即缝间干涉), 运行仿真程序可得如图2(a)所示的光强分布曲线. 由图2(a)可知, 出现了两类极大值, 光强明显大的明纹称为主极大明纹, 而光强远小于主极大的明纹称为次级明纹. 各级主极大明纹对称、等间距地分布在中央明条纹的两侧, 各级主极大明纹的强度几乎相等. 在两个主极大明纹之间存在3条次级明纹.

图2 多缝夫琅禾费衍射的形成分析

以上只考虑了缝间干涉, 并没有考虑光通过每一条狭缝产生的衍射效应对干涉条纹的影响. 事实上由于每一条狭缝衍射的作用, 经多缝屏所形成的干涉明纹并不是等强度分布, 而是受到了单缝衍射光强分布的调制, 屏幕上的光强分布发生了重新分布. 从图2中可看到, 多缝衍射主极大明纹的光强分布包络线与单缝衍射光强分布曲线趋势相同, 主极大和次级明纹的位置主要由缝间干涉决定.

为形象地说明多缝衍射现象的有关影响因素, 仿真实验参数取如下4种组合情况: ①= 5,= 0.001 mm,= 0.006 mm,= 432.8 nm; ②= 10,= 0.001 mm,= 0.006 mm,= 432.8 nm; ③= 10,= 0.001 mm,= 0.006 mm,= 632.8 nm; ④= 5,= 0.003 mm,= 0.012 mm,= 432.8 nm. 从图3中显示的结果可分析得到如下的结论: ①狭缝数目愈大, 则明条纹愈细窄, 次级明纹相对主极大明纹的强度愈小; ②狭缝数目愈大, 则两个主极大之间的次级明纹数目愈多. 一般说来, 如果多缝屏有条狭缝, 则两个主极大之间会有-1条暗纹, 有-2条次级明纹; ③在波长一定时,愈小, 则相邻两个主极大明纹分得愈开; ④在一定时, 波长愈大, 则相邻两个主极大明纹也分得愈开. 总之, 仿真结果与理论和实验结论符合, 达到了很好的演示效果.

图3 多缝衍射图样和光强分布曲线

3.2 多缝夫琅禾费衍射缺级现象分析

多缝夫琅禾费衍射仿真源程序中, 取实验参数= 5,= 0.003 mm,= 0.009 mm,= 432.8 nm,= 1 000 mm, 可得仿真结果如图2(c)和图4所示, 从该两图中可以看到明显的主极大、次极大、中央明纹等现象, 按照缝间干涉在第3级、第6级和第9级等处原本应该出现主极大明纹, 但由于单缝衍射的影响反而变成了暗纹, 这一现象称为缺级. 缺级的条件为:

由式(9)可得:

即当与构成整数比时, 就会出现缺级现象. 式(10)即为缺级条件方程.

因此, 可由式(10)来判断多缝衍射在哪个主极大处出现缺级, 例如:

图4 的多缝衍射图样和光强分布曲线

图5 的多缝衍射图样和光强分布曲线

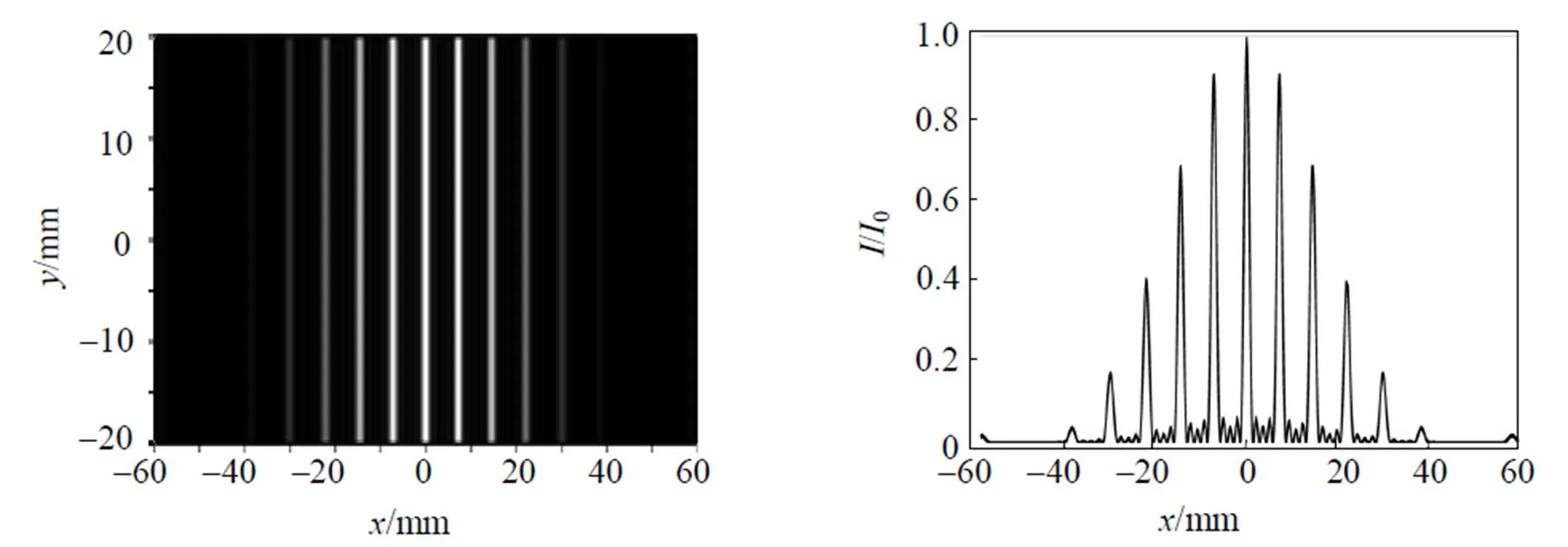
图6 的多缝衍射图样和光强分布曲线

4 结论

本文从惠更斯-菲涅耳原理出发, 得出了单缝和多缝夫琅禾费衍射的光强分布表达式. 在此基础上, 利用Maple软件的数值计算和图形可视化功能, 模拟仿真了多缝夫琅禾费衍射图样的形成及其特点. 结果表明: ①多缝衍射主极大明纹的光强分布包络线与单缝衍射光强分布曲线趋势相同, 主极大和次级明纹的位置主要由缝间干涉决定; ②缝数、相邻透光缝上对应点之间的距离和入射光波长λ等参数对衍射图样有相应影响; ③当与构成整数比时, 就会出现缺级现象. 这些数值仿真模拟形象逼真, 程序编写和运行简单, 实验参数修改方便, 不受实际实验易受条件和环境的限制.

附录1:多缝夫琅禾费衍射图样和光强分布的Maple程序

with(plots):

muti:=proc(N,a,d,lambda)

local M,D,L,PI,xp,A, theta:

M:=50:

D:=100:

if mod(N,2)=1 then

xp:=(k,f)-> -b/2+(f-(M+1)/2)*(d)+k*b/M

else

xp:=(k,f)-> -(a+d)/2+(f-N/2)+k*a/M

end if:

L:= (x,k,f)->sqrt((x-xp(k,f))^2+D^2):

theta:=f->2*Pi*L(x,0,f)/lambda:

A:=proc(x,f)

local i,sumcos,sumsin:

sumcos:=0:

sumsin:=0:

for i from 1 to N do

sumcos:=sumcos+cos(evalf(2*Pi*D(x,i,f)/lambda)):

sumsin:=sumsin+sin(evalf(2*Pi*D(x,i, f)/lambda)):

end do;

evalf((sumcos+I*sumsin)/M);

end proc:

PI:=x->(1/(M*M))*((sum(evalf(abs(A(x, f))*cos(theta(f))),

f =1..M))^2+(sum(evalf(abs(A(x, f))*sin(theta(f))),

f =1..M))^2):

plot(PI(x), x = -60 .. 60, axes = boxed axesfont = ["TIMES NEW ROMAN", "TIMES NEW ROMAN", 14], labels = ["x/mm", "I/I0"], labeldirections = ["horizontal", "vertical"], labelfont = ["TIMES NEW ROMAN", "TIMES NEW ROM- AN", 14]);

end proc:

muti(5, 0.1e-2, 0.6e-2, 0.4328e-3);

muti(10, 0.1e-2, 0.6e-2, 0.4328e-3);

muti(10, 0.1e-2, 0.6e-2, 0.6328e-3);

muti(5, 0.3e-2, 0.9e-2, 0.4328e-3);

muti(5, 0.3e-2, 0.12e-1, 0.4328e-3);

muti1:=proc(N,a,d,lambda)

local M,D,L,PI,xp,A, theta:

M:=50:

D:=100:

if mod(N,2)=1 then

xp:=(k,f)-> -b/2+(f-(M+1)/2)*(d)+k*b/M else

xp:=(k,f)-> -(a+d)/2+(f-N/2)+k*a/M

end if:

L:= (x,k,f)->sqrt((x-xp(k,f))^2+D^2): theta:=f->2*Pi*L(x,0,f)/lambda:

A:=proc(x,f)

local i,sumcos,sumsin:

sumcos:=0:

sumsin:=0:

for i from 1 to N do

sumcos:=sumcos+cos(evalf(2*Pi*D(x,i,j)/lambda)):

sumsin:=sumsin+sin(evalf(2*Pi*D(x,i,j)/lambda)):

end do;

evalf((sumcos+I*sumsin)/M);

end proc:

PI:=x->(1/(M*M))*((sum(evalf(abs(A(x, f))*cos(theta(f))),

f =1..M))^2+(sum(evalf(abs(A(x, f))*sin(theta(f))), f =1..M)) ^2):

plot3d([x, y, PI(x)], x = -60 .. 60, y = -20 .. 20, grid = [150, 150], orientation = [270, 0], shading = ZGRAYSCALE, style = PATCHNOGRID, numpoints = 20000, axes = boxed,axesfont = ["TIMES NEW ROMAN","TIMES NEW ROMAN", "TIMES NEW ROMAN", 14], labels = ["x/mm", "y/mm",""], labeldirections = ["horizontal" ,"vertical","horizontal"], labelfont = ["TIMES NEW ROMAN", "TIMES NEW ROMAN", 14])

end proc;

muti1(5, 0.1e-2, 0.6e-2, 0.4328e-3);

muti1(10, 0.1e-2, 0.6e-2, 0.4328e-3);

muti1(10, 0.1e-2, 0.6e-2, 0.6328e-3);

muti1(5, 0.3e-2, 0.9e-2, 0.4328e-3);

muti1(5, 0.3e-2, 0.12e-1, 0.4328e-3).

[1] 胡盘新, 钟季康. 在大学物理教材中引入计算机数值解的尝试[J]. 物理与工程, 2006, 16(2): 47—50.

[2] 华晋, 尹金花. 基于GUI的干涉衍射的实验教学研究[J]. 大学物理实验, 2011, 24(1): 79—82.

[3] 王悦悦, 赵丽华, 吴雷. Maple在光学实验中的应用[J]. 物理与工程, 2009, 19(4):17—23.

[4] 赵凯华, 钟锡华. 光学[M]. 北京: 北京大学出版社, 1982: 170.

[5] 马文蔚. 物理学[M]. 北京: 高等教育出版社, 2006: 254.

[6] 何青, 王丽芬. Maple教程[M]. 北京: 科学出版社, 2006: 21—89.

[7] 汤剑锋, 赵凡. 夫琅禾费衍射实验的Maple仿真设计[J]. 湖南文理学院学报: 自然科学版, 2011, 23(4): 37—41.

Computer simulation of the multiple-slit Fraunhofer diffraction experiment

DENG Lei, TANG JianFeng

(College of Science, Hunan Agricultural University, Changsha 410128, China)

To better explain multiple-slit Fraunhofer diffraction in real terms, the multiple-slit Fraunhofer diffraction was simulated by using the Maple software.Their diffraction patterns and light intensity distributioncurves were drawn. By changing adjustable parameters, the light intensity distribution features and the influential factors of the multi-slit diffraction missing order phenomenon are analyzed in some detail. The research shows that the results of numerical simulation are completely coordinated with actual experiments, and the arithmetic is easy to be realized and convenient in teaching due to its intuitionistic simulation effects.

multiple-slit Fraunhofer diffraction; missing orders phenomenon;Huygens-Fresnel principle; Maple software

10.3969/j.issn.1672-6146.2014.04.015

O 436.1

1672-6146(2014)04-0059-06

email: hnjftang@aliyun.com.

email: lei0736@aliyun.com.

2014-07-05

湖南省普通高等学校教学改革研究项目(2014166); 中华农业科教基金教材建设项目(NKJ201202005).

(责任编校:刘刚毅)