基于粒子群优化偏最小二乘的铁路客运量预测

梁小林, 杜晓慧



基于粒子群优化偏最小二乘的铁路客运量预测

梁小林*, 杜晓慧

(长沙理工大学 数学与计算科学学院, 湖南 长沙, 410076)

通过对1997—2012年铁路客运量的影响因素进行分析, 建立偏最小二乘回归模型, 并用实际的铁路客运量与预测值进行比较, 检验出模型的预测误差较大. 为了提高模型的预测精度, 采取粒子群优化算法优化回归系数, 得到一个新的模型. 经检验, 该模型的预测误差由原模型的3.04%降到1.01%. 最后用该模型预测出2013—2014年的铁路客运量分别为210.970 5千万人和227.368 8千万人.

偏最小二乘; 粒子群优化; 铁路客运量; 预测

铁路客运量预测是对客运量的发展趋势进行分析, 由于影响铁路客运量的因素错综复杂, 使得对铁路客运量预测建模非常困难. 传统的预测方法有: 线性回归法[1]、支持向量机[2—3]、灰色马尔科夫模型法[4—5]、神经网络模型法[6]等, 它们大部分都是预测短时间内客运量的变化趋势, 并且是通过前几年的铁路客运量来预测, 没有考虑到影响客运量的一些因素, 因而预测效果不理想. 本文从影响铁路客运量的关键因素出发, 利用偏最小二乘法和粒子群优化算法来研究铁路客运量问题.

1 偏最小二乘回归法

传统的线性回归方法可以很好的对相关性很小的变量进行拟合和预测, 但是当变量之间存在严重相关性时, 再采用最小二乘求解拟合方程就不能得到好的预测模型. 然而, 偏最小二乘回归方法[7]的一个突出特点是将主成分分析、典型相关分析与多元线性回归分析方法结合起来, 同时实现了数据结构简化、回归建模和变量之间的相关分析, 为多元数据分析提供了很大的方便, 并且在处理样本少、变量多、变量之间存在多重共线性问题有很好的优势.

偏最小二乘的建模步骤:

2 粒子群优化算法

粒子群优化算法是一种新的进化算法, 同遗传算法类似, 都是一种基于群体迭代的优化算法[8]. 首先初始化一群随机粒子, 然后通过迭代计算寻找到最优解. 但它比遗传算法更简单一些, 它没有遗传算法的交叉和变异操作, 它通过追寻当前搜索到的最优值来寻找全局最优解.

3 粒子群优化的偏最小二乘回归

粒子群优化的偏最小二乘回归模型的主要思想是: 把偏最小二乘的回归系数作为最初的粒子位置, 偏回归系数周围的区域可以作为它的目标区域, 通过迭代寻找到最优的解, 直到达到满意的结果为止. 具体步骤如下:

a. 通过建立的偏最小二乘回归方程, 把未标准化的回归系数作为目标变量来对其进行优化, 并对粒子群的随机位置和速度进行初始设定.

b. 固定适应度函数. 定义适应度函数如下:

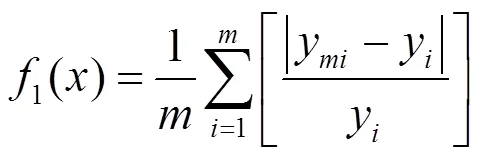
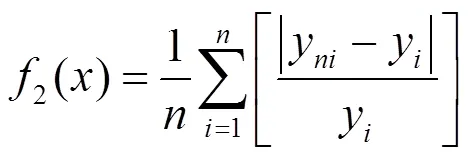
e. 根据2个迭代公式对粒子的速度和位置进行进化;

f. 若达到了足够好的适应值, 则执行第g步; 否则再执行步骤b;

g. 输出最优结果.

4 实证研究

4.1 指标选取及数据处理

表1 1997—2012年铁路客运量预测分析指标

从表1可以看出, 铁路客运量的数据有明显上升的趋势. 但2003年的铁路客运量的数据却急剧下降, 是因为2003年发生了SARS病毒感染, 因此在建模过程中可以去掉2003年的数据. 采用1997—2007年的6个变量的数据作为自变量, 1999—2009年的铁路客运量作为因变量来建立回归模型, 为了方便对结果进行检验, 选取2010—2012年的模型预测的铁路客运量结果进行检验.

4.2 相关性分析

表2 相关性分析

注: **在0.1水平(双侧)上显著相关.

4.3 建立偏最小二乘回归模型

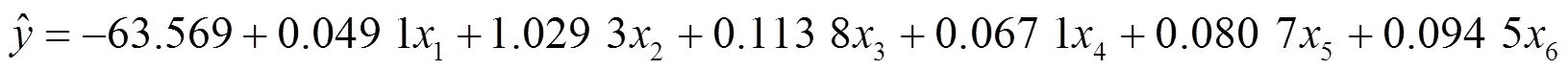
4.4 建立粒子群优化的偏最小二乘回归模型

表3 1999—2009年铁路客运量预测值

通过该模型可以算出铁路客运量的相关数值，结果如表3所示.

该模型预测出来的2010—2012年的铁路客运量如表4所示.

从表3和表4可以看出, 优化后的模型预测误差相对小一些, 实际偏最小二乘模型的平均拟合误差和平均预测误差分别为1.4%和3.04%, 而粒子群优化后的偏最小二乘模型的平均拟合误差和平均预测误差分别为1.04%和1.01%, 可见改进后模型的预测性能更好, 误差更小. 为了验证模型的预测性能好, 与文献中预测的我国铁路客运量进行比较, 李晓东[5]通过线性回归与马尔科夫理论结合起来预测2011—2012年的铁路客运量, 预测误差比本文模型预测出来的

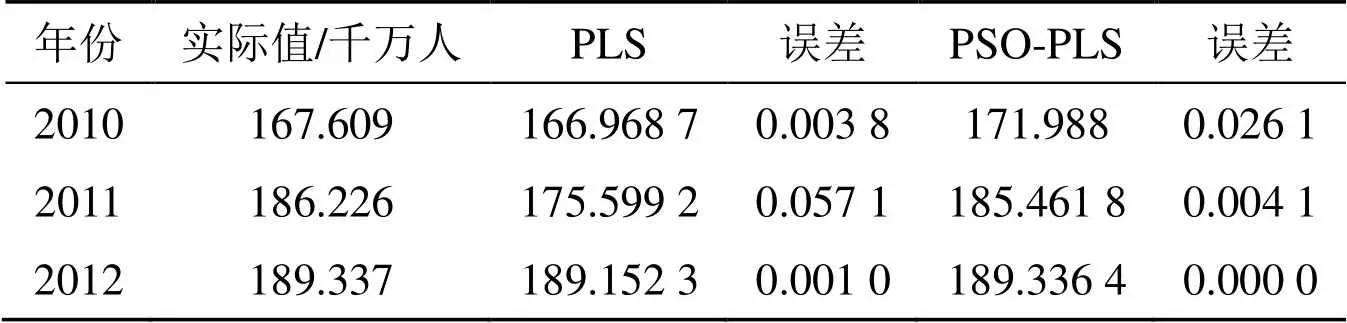
表4 2010—2012年铁路客运量预测值

误差大. 朱伟[3]通过粒子群优化支持向量机, 虽然预测的铁路客运量的时间不一样, 但是它的预测误差

达到5%左右, 明显没有本文模型的预测效果好. 因此, 考虑影响铁路运客运量的因素来对铁路客运量进行预测, 本文模型能得到很好的预测效果.

通过图1, 可以明显看出优化后模型的预测值更接近真实值, 因此可以用该模型来预测2013年和2014年的铁路客运量, 通过把2011年和2012年的自变量的指标代入所建立的新的回归方程(4)中, 预测出2013年和2014年的铁路客运量分别为210.970 5千万人和227.368 8千万人.

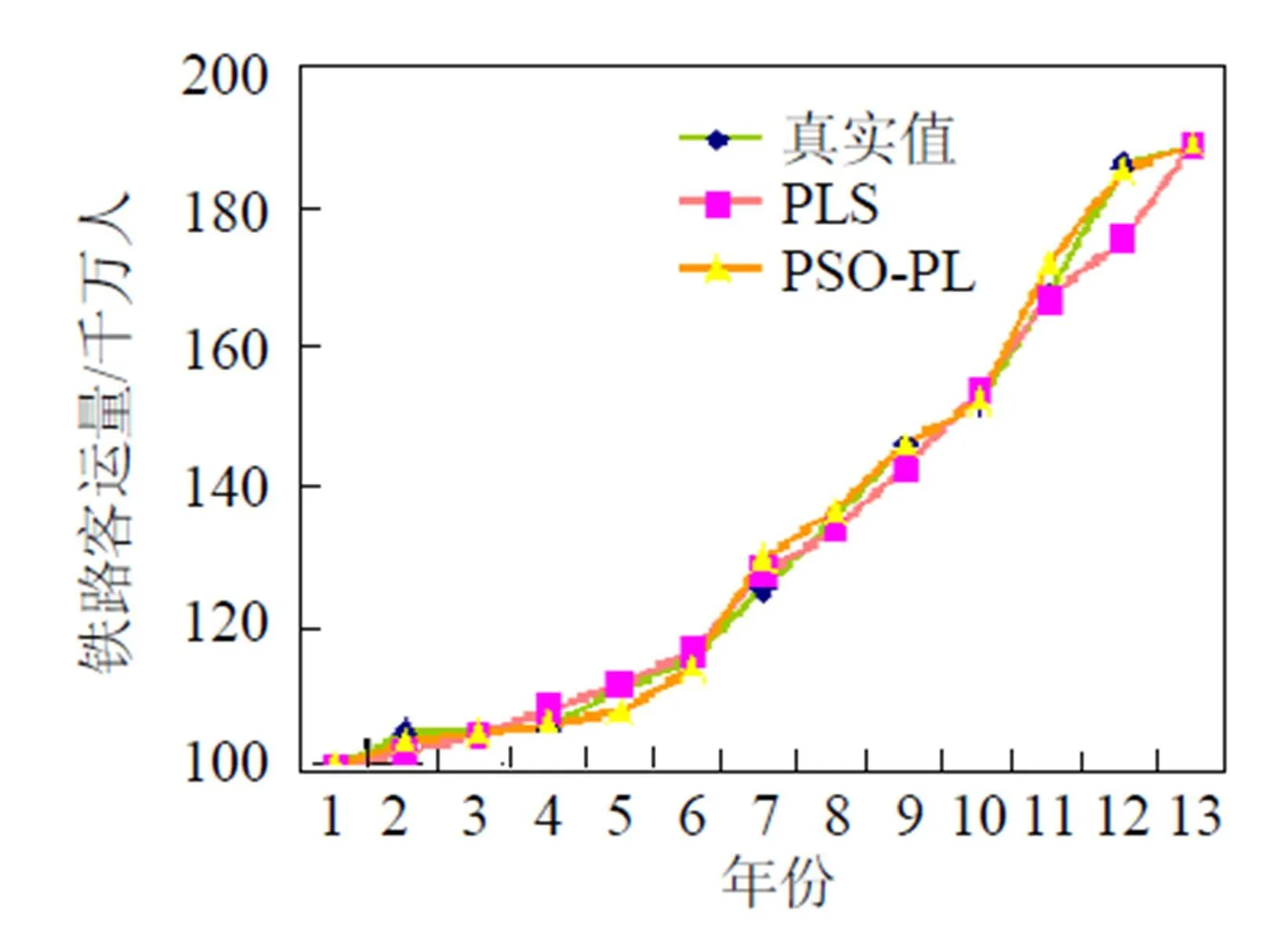
图1 优化后模型铁路客运量结果. 横标数据1, 2, 3, …, 13分别表示2001, 2002, 2003, …, 2013年.

5 小结

本文利用粒子群优化算法来优化偏最小二乘回归, 对其回归系数进行优化, 来改进模型的预测精度. 通过对影响铁路客运量的因素进行分析, 来预测铁路客运量, 利用该模型预测出的2010—2012年的铁路客运量的预测值与真实值进行比较, 得出预测误差很小的结论. 并用该模型预测了2013—2014年的铁路客运量, 对铁路部门进行相关决策起到应有的作用.

[1] 杜先汉, 李岩. 基于灰色关联理论与多元线性回归模型的铁路客运量预测[J]. 交通科技与经济, 2013, 15(4): 90—93.

[2] 姜华, 曹红妍. 基于最小二乘支持向量机的铁路客运量预测研究[J]. 河南科学, 2010, 28(8): 89—92.

[3] 朱伟, 李楠等. 基于粒子群算法优化支持向量机的铁路客运量预测模型[J]. 商丘师范学院学报, 2013, 29(12): 33—36.

[4] Zhang Wei, Zhu Jinfu. Passenger Traffic Forecast based on the Grey-Markov Method [A]. Grey Systems and Intelligent Services IEEE International Conference [C]. Nanjing, 2009: 630—633

[5] 李晓东. 基于线性回归-马尔科夫模型的铁路客运量预测[J]. 铁道运输与经济, 2012(4): 38—42.

[6] 谢小山, 李远富.GA-BP算法的铁路客运量预测[J]. 西南交通大学学报, 2009, 44(增):782—785.

[7] 王惠文. 偏最小二乘的线性与非线性方法[M]. 北京: 国防工业出版社, 2006.

[8] 刘波. 粒子群优化算法及其工程应用[M]. 北京: 电子工业出版社, 2010.

Forecast of railway passenger traffic based on PLS of particle swarm optimization

LIANG XiaoLin, DU XiaoHui

(School of Mathematics and Computing Sciences, Changsha University of Science & Technology, Changsha 410076, China)

By analyzing the influence factors of railway passenger traffic from 1997 to 2007, partial least-squares regression model were established, then actual and predicted values of railway passenger traffic were compared, and the model prediction error was relatively high. In order to improve the prediction accuracy of the model, PSO optimization algorithm was adopted to optimize the regression coefficients, then a new model was got. Upon examination, the prediction error of the model dropped to 1.01% from original 3.04%. Finally the railway passenger traffic from 2013 to 2014 which we use this model to predict were 2 109.705 million and 2 273.688 million.

partial least squares; particle swarm optimization; railway passenger traffic; forecast

10.3969/j.issn.1672-6146.2014.04.002

O 212

1672-6146(2014)04-0006-05

email: 494737721@qq.com.

2014-07-28

国家自然科学基金资助项目(11171044); 湖南省研究生课题资助(JG2013B040).

(责任编校:刘晓霞)