Al、Ti、Cu、Mo和Au类氦离子光谱跃迁的理论研究

易有根, 叶显爵, 谢海军, 朱正和



Al、Ti、Cu、Mo和Au类氦离子光谱跃迁的理论研究

易有根*1, 叶显爵1, 谢海军1, 朱正和2

(1. 中南大学 物理与电子学院, 湖南 长沙, 410083; 2. 四川大学 原子与分子物理研究所, 四川 成都, 610065)

采用广义平均能级EAL模型和相对论量子力学GRASP2程序, 考虑到核的有限体积效应、磁场效应、Breit和QED效应等修正, 系统地计算了Al、Ti、Cu、Mo和Au类氦离子光谱跃迁的跃迁波长、跃迁几率和振子强度, 所得结果和实验数据及其它计算值进行了比较. 计算结果表明: 在ICF和MCF高温激光等离子体中, 类氦离子光谱的跃迁几率过程不能被忽视, 可用来诊断稠密等离子体的磁场效应.

高剥离态; 类氦离子; 能级间隔; 跃迁几率; 振子强度

随着强场物理的发展, 人们对超短超强激光与等离子体相互作用中产生的自生磁场越来越重视, “快点火”的提出使自生磁场研究成为新的热点. 最近几年超短超强激光与等离子体相互作用中产生的自生磁场的理论研究和实验研究取得了长足的进展[1]. 在用三维粒子数值模拟研究圆偏振激光与高密度等离子体作用中, 观察到逆法拉第效应产生的高达100 MG的轴向磁场. 研究还发现这个磁场对高能电子流有很好的箍缩和准直效应, 并且有助于使圆偏振激光传入到与线偏振激光相比的更稠密的等离子体区域[2].

上世纪90年代, Wilks[3]等人用数值模拟研究光强在1018W/cm2以上的超短脉冲激光与高密度等离子体作用中发现, 由于激光场对靶表面的等离子体电子的强烈加热, 在靶表面产生超过100 MG(MG即为兆高斯)的准静态磁场. 美国康乃尔大学的Sudan[4]以及马里兰大学刘全生和Tripathi对上述磁场产生机制进行了理论分析, 认为由于入射激光的有质动力对电子的推动以及随后产生的迟滞的屏蔽电子回流的共同作用, 产生所观察到的磁场. Manson等[5]用ANTHEM程序首次对高激光强度(>3´1018W/cm2)下大密度范围(0.35～200)c等离子体内的自生磁场进行了模拟, 结果显示产生了16～250 MG的强磁场, 该磁场与Sudan提出有质动力产生磁场的理论一致. 靶表面及其内部的强磁场产生与发展是与作用过程中产生高能电子的输运密切相关的, 其中所谓的Weibel电磁不稳定的发展对强磁场的产生起重要作用. 因此可以说在激光与固体靶作用中在固体靶表面产生的准静态磁场是多种机制共同作用的结果. Teychenne等[6]提出, 超短超强激光与固体靶相互作用瞬态场电离可激发稳态磁场. Macchi等[7]用1D3VPIC模拟研究了薄膜靶中瞬态场电离产生的磁场, 发现在靶面产生了稳态MG磁场, 且磁场大小取决于靶材的电离阈值. Bhattacharyya等[8]研究了环形磁场和轴向磁场同时产生的机制, 数字模拟结果显示: 环形磁场和轴向磁场随激光强度的增加而增加, 环形磁场随激光脉冲的长度增加而减小且随激光波长的增加十分缓慢的增加, 轴向磁场对激光脉冲的长度并不敏感, 但随激光波长呈指数地增加. Pukhov[9]在用3D模拟研究离子加速时发现, 在实验研究方面, Borghesi[10]等利用光学探针束, 对自生磁场进行了时空测量, 发现了MG的强磁场. Tatarakis等[11]在超高强度(～1019W·cm-2)短脉冲(0.7～1.0 ps)与固体靶相互作用中采用自生谐波的极化方法测量了磁场, 磁场强度达到340～460 MG. 依据Stark或Doppler效应产生原子光谱的精细结构和谱线形状, 可以确定磁场的大小.

本文根据广义平均能级EAL模型和相对论量子力学GRASP2程序, 考虑到核的有限体积效应、磁场效应、Breit和QED效应等修正, 系统地计算了Al、Ti、Cu、Mo和Au类氦离子1s2 1S0-1s2p1P1、1s2 1S0-1s2p3P1、1s2 1S0-1s3p1P1和1s2 1S0-1s3p3P1光谱跃迁的跃迁波长、跃迁几率和振子强度, 计算结果表明: 在ICF和MCF高温激光等离子体中, 类氦离子光谱的跃迁几率过程不能被忽视, 可用来诊断稠密等离子体的磁场效应.

1 基本理论与方法

在相对论多组态Dirac-Fock理论中[12—14],电子原子或离子体系的Hamiltonian量为:

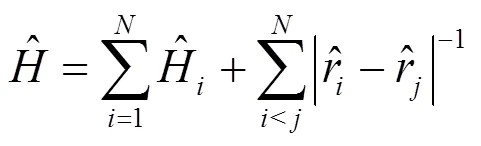
第个电子的Dirac-Coulomb Hamiltonian量, 它由式(2)给出:

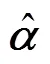
考虑到能量函数和径向波函数有关, 得到了相对论自洽场方程如下:

径向波函数nk()和nk()可以用自洽场迭带方法通过求解径向Dirac方程得到, 以Breit修正和量子电动力学效应修正(包含自能和真空极化能)作为微扰, 可得到能量和波函数的高阶近似.

对目前的计算, Dirac-Fock能级值中包含了Breit修正和QED修正, 其中Breit修正能包括磁衰变能和退化能, QED修正能包括自能和真空极化能. 因此, 对一个给定的原子或离子的能级值, 总能级可以表述为:

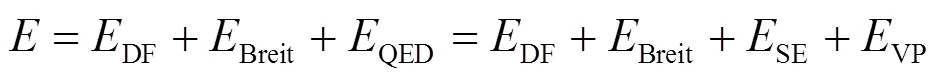
其中DF能量通过求解多组态Dirac-Fock方程而获得.

Breit相互作用能由下式给出:

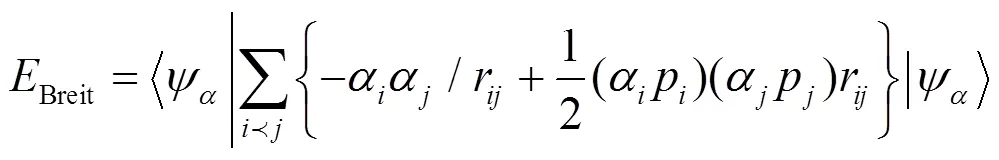
自能对QED的关联能贡献是:

其中F(/c)表的内插数值,是主量子数,q是轨道占有数,º[nkm]. 真空极化能贡献由下式计算:

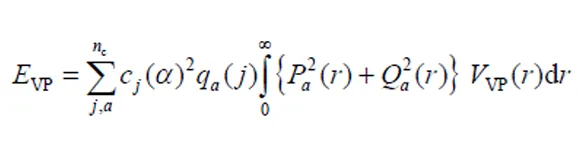
其中VP()是真空极化势,c(表示角动量)是能级混合系数和,c是组态状态函数CSF的数目.

根据含时微扰理论, 单位时间内(0= h3/(e4))从上能态|′′′ >到所有低能态|>的爱因斯坦自发辐射的跃迁几率为:

单位时间内从原子态Г到Г原子态的光谱线跃迁的振子强度为:

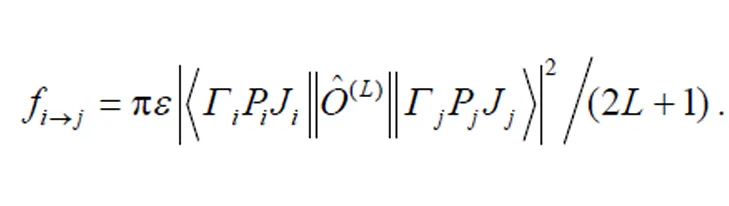
2 计算结果与讨论

计算中采用2参数费米(Fermi)有限核电荷分布、广义平均能级模型(EAL), 考虑核的体积效应、磁场效应、Breit修正、QED 修正, 自洽场迭代精度一般优于10-8. 选取11个电子组态1s2、1s2s、1s3s、1s2p、1s3p、1s3d、2s2、2s3s、2s2p、2s3p和2s3d, 用这11个电子组态耦合出32个组态状态波函数CSF, 进而用其来构造原子状态函数ASF. 由1s2p、1s3p、2s2p和2s3p耦合得到的奇态CSF存在非动力学组态相关, 由1s2、1s2s、1s3s、2s2、2s3s和2s3d, 耦合得到的偶态CSF存在动力学组态相关. 一般而言, 原子状态函数ASF是电子组态状态函数CSF的线性迭加. 表1—表3中分别列出了采用的32电子组态对镍类氦离子1s2 1S0-1s2p1P1、1s2 1S0-1s2p3P1、1s2 1S0-1s 3p1P1和1s2 1S0-1s3p3P1光谱跃迁的轨道估算值, Cou- lomb、Breit和QED对其能级的贡献以及与CIV3计算方法的能级比较, 类氦镍离子激发态原子能级与其它方法的能级比较. 计算结果与实验值以及用其它方法计算值比较接近[16], 在计算原子的镍类氦离子精细结构能级间隔时, Breit修正和QED量子电动力学关联效应修正均不能被忽略, Breit修正一般比QED修正要小些. 原子单位a.u.与国际单位米的换算关系为a.u.= 0.219 472 74 ×106m-1.

表1 类氦镍离子轨道估算值

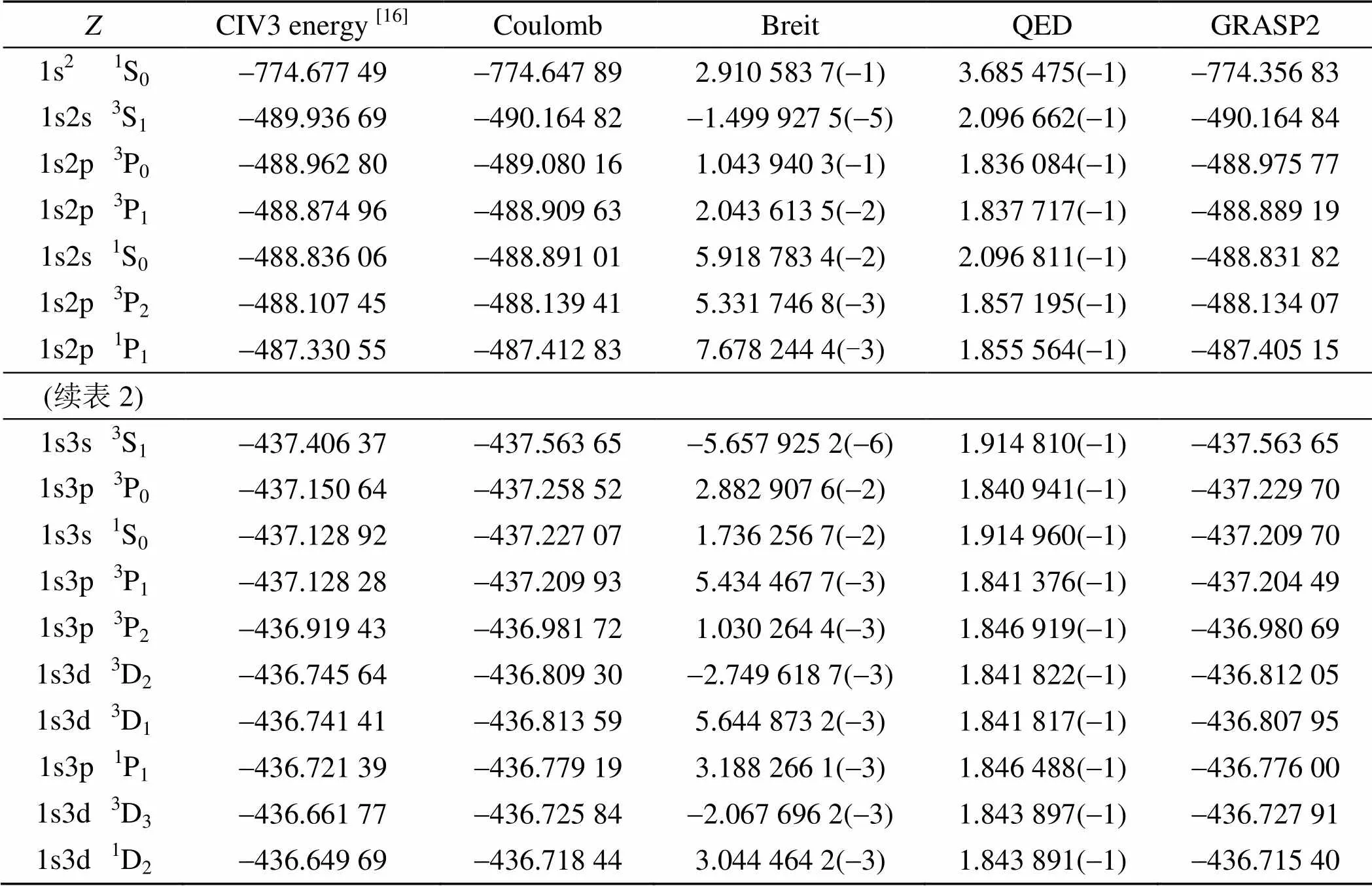
表2 类氦镍离子Coulomb、Breit和QED对能级的贡献及与CIV3计算方法的能级比较/a.u.

注: 表中()表示× 10

表4—表5计算了Al、Ti、Cu、Mo和Au类氦离子1s2 1S0-1s2p1P1、1s2 1S0-1s2p3P1、1s2 1S0-1s3p1P1和1s2 1S0-1s3p3P1光谱跃迁能级间隔、跃迁几率和振子强度. 计算过程中发现, 沿整个等电子序列Breit修正和QED量子电动力学关联效应修正均随着核电荷数的增加而增加. Breit修正和QED量子电动力学关联效应均不能被忽略, Breit修正一般比QED修正大1至几个数量级. Breit相互作用修正和量子电动力学QED效应修正对精细结构能级作了重要的贡献, 尤其是对高离化重元素原子离子. 由于量子电动力学(QED)效应与高次幂成比例, QED效应在高离化态高原子就变得比较重要, 尤其是对高元素的高离化态的重离子而言.

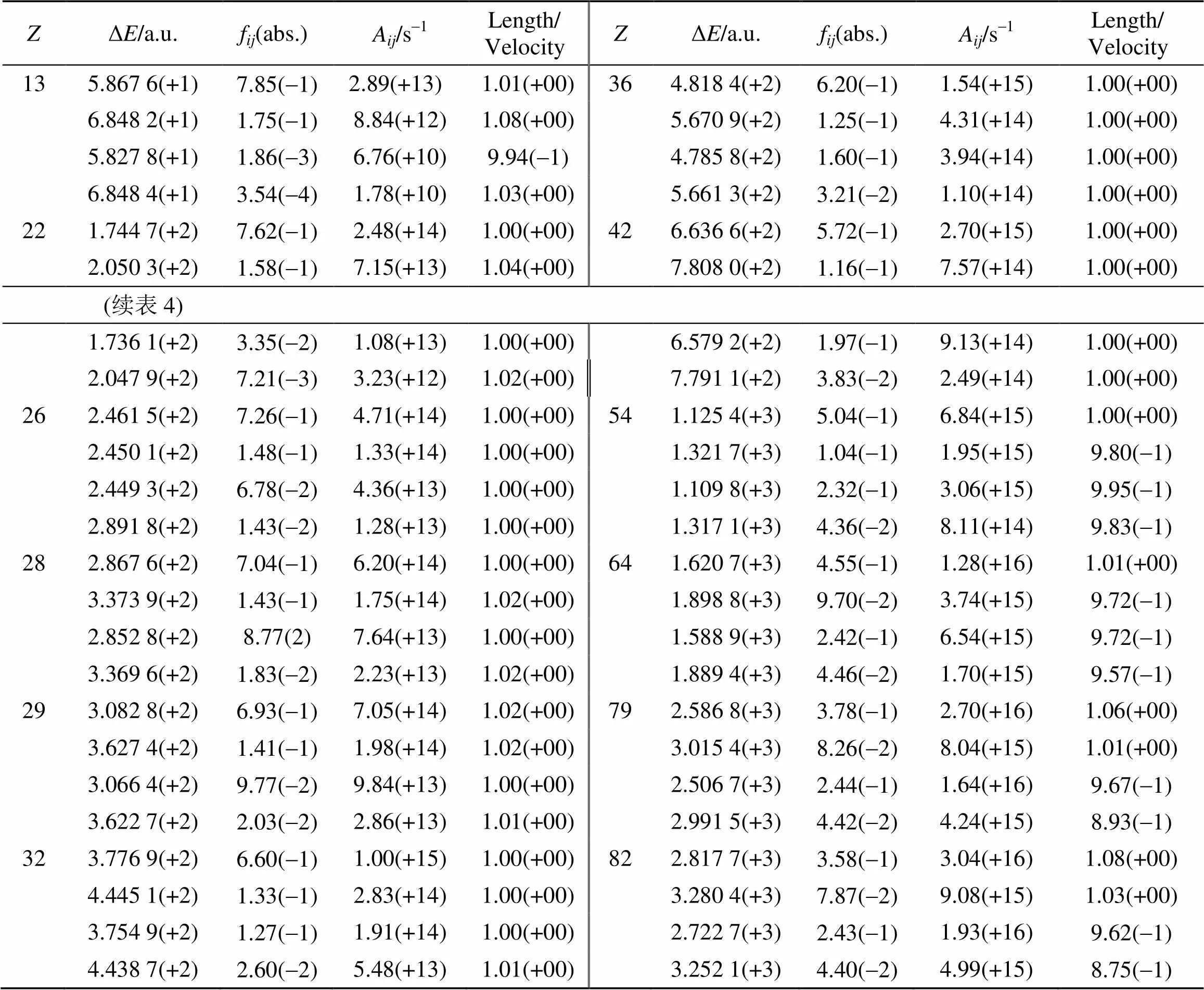
表4 Al、Ti、Cu、Mo和Au类氦离子光谱跃迁能级间隔、跃迁几率和振子强度 (Z = 13～82)

注: 表中()表示× 10

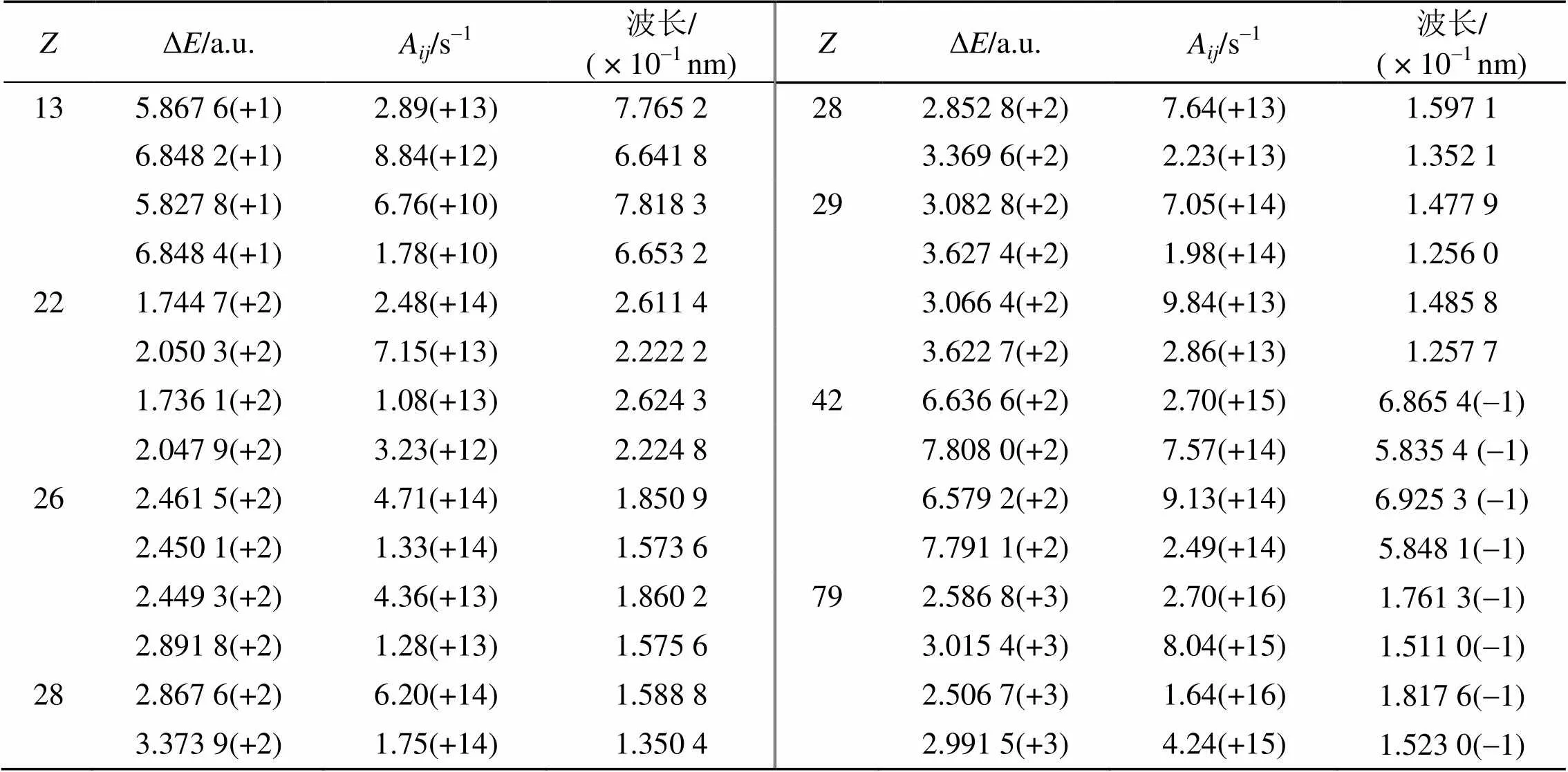
表5 Al、Ti、Cu、Mo和Au类氦离子光谱跃迁的能级间隔、跃迁几率和跃迁波长

注: 表中()表示× 10

3 结论

选取11个电子组态1s2、1s2s、1s3s、1s2p、1s3p、1s3d、2s2、2s3s、2s2p、2s3p和2s3d, 带有Breit和QED修正, 2参数费米(Fermi)有限核电荷分布, 采用多组态Dirac-Fock平均能级方法和全相对论量子力学GRASP2计算程序系统计算了Al、Ti、Cu、Mo和Au类氦离子1s2 1S0-1s2p1P1、1s2 1S0-1s2p3P1、1s2 1S0-1s3p1P1和1s2 1S0-1s3p3P1光谱跃迁能级间隔、跃迁几率和振子强度. 得出如下主要结论: ①采用多组态相对论自洽场方法, 结果表明, Breit修正和QED修正会使得类镁离子部分精细结构能级间隔发生交错和倒置, 且沿整个等电子系列Breit修正和QED修正均随核电荷数的增加而增加. 对离化程度很高的重元素原子离子, 其间存在更强的Breit修正效应和量子电动力学QED修正效应; ②尽管低值时, 类氦离子光谱跃迁的自发跃迁几率很小, 一般而言, 电偶极过程的自发跃迁几率为107～109s-1, 然而, 高高离化原子离子的类氦离子光谱跃迁过程的却超过中性原子电偶极跃迁过程的自发跃迁几率; ③随着原子的核电荷数增加, 类氦离子光谱跃迁的计算结果的精细结构间隔光谱项从LS耦合过渡到J-J耦合. 对于高电荷重离子类镁离子谱项为典型的J-J耦合; ④从理论上预言了激光等离子体Al、Ti、Cu、Mo和Au类氦离子1s2 1S0-1s2p1P1、1s2 1S0-1s2p3P1、1s2 1S0-1s3p1P1和1s2 1S0-1s3p3P1光谱跃迁的精细能级结构间隔、跃迁波长、跃迁几率和振子强度.

[1] Shen Z M, Mever-ter-Vehn J. Inverse Faraday effect and propagation of circularly polarized intense laser beams in plasmas [J]. Phys Rev E, 1996, 54(2): 1833—1842.

[2] Zheng C Y, He X T. Magnetic field generation and relativistic electron dynamics in circularly polarized intenser laser interaction with dense plasma [J]. Physics of plasmas, 2005, 12: 044505-01.

[3] Wilks S C, Kruer W L, Tabak M, et al. Absorption of ultra-intense laser pulses [J]. Phys Rev Lett, 1992, 69: 1383—1386.

[4] Sudan R N. Mechanism for the generation of 109G magnetic fields in the interaction of ultraintense short laser pulse with an overdense plasma target [J]. Phys Rev Lett, 1992, 70: 3075—3078.

[5] Mason R J, TabakM. Magnetic field generation in high-intensity-laser–matter interactions [J]. Phys Rev Lett, 1998, 80: 524—527.

[6] Teychenné D, Giulietti A, Giulietti D, et al. Magnetically induced optical transparency of overdense plasmas due to ultrafast ionization [J]. Phys Rev E, 1998, 58: 1245—1247.

[7] Macchi A, JarqueE C, BauerD, et al. Steady magnetic field generation due to transient field ionization in ultrashort laser-solid interaction n[J]. Phys Rev E, 1999, 59: 36—39.

[8] BhattacharyyaB, SanyalU, LawandeS V, et al. Model for the generation of toroidal and poloidal magnetic fields in a laser-produced plasma [J]. Phys Rev E, 2000, 63(1 Pt 2): 016404-01.

[9] Pukhov A. Three-dimensional simulations of ion acceleration from a foil irradiated by a short-pulse laser [J]. Phys Rev Lett, 2001, 86: 3562—3565.

[10] Borghesi M, MacKinnon A J, Bell A R, et al. Megagauss magnetic field generation and plasma jet formation on solid targets irradiated by an ultraintense picosecond laser pulse [J]. Phys Rev Lett, 1998, 81: 112—115.

[11] Fuchs J, Adam J C, Borghesi M, et al. Experimental study of laser penetration in overdense plasmas at relativistic intensities. II: Explosion of thin foils by laser driven fast electrons [J]. Phys Plasmas, 1999, 6: 2569—2572.

[12] 杨富利, 易有根. 类钾离子4s S1/2─3d D3/2电四极矩2光谱跃迁的理论研究[J]. 物理学报, 2008, 57(3): 1622 —1625.

[13] 欧阳永中, 易有根, 朱正和, 等. 类铍离子磁四极2 2s21S0-2s2p3P2(= 10～103)禁戒跃迁[J]. 物理学报, 2007, 56(7): 3880—3886.

[14] Grant I P. Gauge invariance and relativistic radiative transitions[J]. J Phys, 1974, B7: 1458—1475.

[15] Harra L K, Boone A W, Norrington P H, et al. Energy levels and oscillator strengths for transitions in helium-like Ni XXVII [J]. J phys B, 1993, 26: 2543—2553.

Theoretical study of spectral transition of He-like Al, Ti, Cu, Mo and Auions

YI YouGen1, YE XianJue1, XIE HaiJun1, ZHU ZhengHe2

(1. College of Physics and Electronics, Central South University, Changsha 410083, China; 2. Institute of Atomic and Molecular Physics, Sichuan University, Chengdu 610065, China )

A fully relativistic multiconfiguration Dirac-Fock method with Breit and QED corrections was used to calculate transition energy level separations, transition probabilities and oscillator strengths for the He-like Al, Ti, Cu, Mo and Au ions. In calculation, the significant magnetic field effects and Breit and QED corrections were considered. The results were compared with recent experimental data and other theoretical values. The results show that the electric transition probabilities were significant and can not be ignored in the laser plasma of high temperature in ICF and MCF Fusion.

highly stripped ion; He-like ions; transition energy level; transition probability; oscillator strength

10.3969/j.issn.1672-6146.2014.04.004

O 571.4

1672-6146(2014)04-0016-06

email: yougenyi@163.com.

2014-05-08

国家自然科学基金(10275056); 中南大学本科生自由探索计划项目(2282013bks022)

(责任编校:刘刚毅)