基于最小二乘法引导的信赖域算法在电力系统动态负荷参数辨识中的应用

肖阳，康忠健，马晓炜

（1.中国石油大学（华东）电气工程系，山东青岛 266580；2.新疆石油勘察设计研究院（有限公司）电气所，新疆克拉玛依 834000）

近些年来，伴随着电网安全要求的日益提高，电压稳定，特别是暂态电压稳定分析的重要性和准确性日渐成为研究者们关注的重点。暂态电压稳定是以分析系统受到扰动后短时间内是否稳定为研究目的，以动态分析最为有效，其相比静态电压稳定分析更注重系统的动态过程对研究结果的影响，负荷模型能否反映系统动态特性和实际运行状态直接关系到研究结果的准确性[1-2]。动态建模方法在自然科学和工程领域的广泛应用，这种能够利用被控系统的输入数据和输出数据来估算系统中未知参数的能力，在电力系统电压稳定性分析，特别是暂态电压建模稳定分析中，有着重要的意义[3]。动态建模的需求促进了电力系统辨识技术的广泛应用。

系统辨识作为系统科学的一个分支，虽是一门较为新型的学科，但已成为各个领域和行业中必不可少的分析手段和运算方法，就电力系统领域而言，系统辨识在数据处理、在线调试、故障检测、工况预报、动态等值等方面提供新的解决方案[4]。例如最小二乘法，卡尔曼滤波法等，多是适用于线性系统[5-6]，而电力系统本质上是一种非线性高阶复杂随机系统，只能采用一些线性化或扩展化的近似方法解决此类问题，容易产生收敛和局部最优等问题。

基于二次插值的信赖域算法是一种最优化求解算法[7-8]。最优化算法的种类比较多，按照是否需要计算梯度可分为3类：梯度类算法、无梯度类算法和人工智能算法。人工智能算法本质上也属于无梯度类算法，但由于人工智能算法是通过仿生技术来解决和处理复杂问题，因此将其独立于无梯度类算法单独列为一类。基于二次插值的信赖域是一类目标函数近似逼近的无梯度算法，为提高其计算效率，满足工程需要，有学者提出一种改进的由近似梯形引导的二次插值模型方法对油藏数值进行模拟运算。在油藏生产优化领域有较好的应用，但对电力系统领域而言，此方法还未能广泛应用。

本文针对动态负荷模型参数辨识问题，提出结合最小二乘法思想，应用基于二次插值的信赖域法对动态负荷模型参数进行辨识，并应用IEEE的3机9节点标准模型验证了该算法的有效性。

1 动态负荷参数辨识模型的构建

电力系统分析数学模型是电力系统离线分析的重要手段之一。传统的数学模型是以物理机理为基础，参数以铭牌数据或经验参数为主，实际参数与设定值有较大差异。利用动态辨识建模可做到与实际运行方式相符。本文针对动态负荷模型构建其参数辨识模型。

通常可以将负荷动态模型分为3种：机械暂态过程负荷模型、机电暂态过程负荷模型和电磁暂态过程负荷模型。以上3种模型中，机械暂态过程负荷模型和机电暂态过程负荷模型较为常见，而仅有在考虑电磁暂态过程时，才使用电磁暂态负荷模型。本文不考虑系统电磁暂态过程，以简单的机械暂态负荷模型为例，说明算法原理。负荷模型如图1所示。

图1 考虑机械暂态过程的动态负荷模型Fig.1 The dynam ic load model diagram considering the mechanical transient process

图1中，UL为三相对称母线电压；IL为相应感应电机电流，滑差为s，rs和Xs是定子电阻和漏抗；rr和Xr为转子等值电阻和漏抗；rr和Xm为铁损的等值电阻和漏抗，则可得其等值阻抗如式（1）所示[4]：

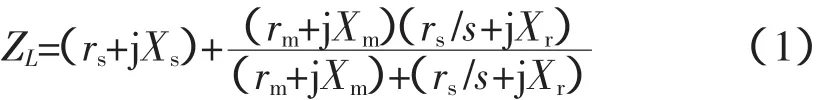
式中，rs、Xs、rr、Xr、rm、Xm和s为待辨识的7个未知量。本文借用最小二乘法思想，即估计点与采样点之间的距离最小，对式（1）进行相应的引导变换，得到信赖域算法所需适应度函数。构建采样点与估计点距离函数：

式中，ZL即为含有待辨识参数的等值阻抗方程；Z（LX）为通过实际测量电压电流值求取的等值阻抗值，求取G（LX）最小值。可以认为每一组Z（LX）-ZL的值都为最小值。将式（2）转化为求取一系列Z（LX）-ZL=0的非线性方程组，对G（LX）分别关于rs、Xs、rr、Xr、rm、Xm和s求取雅克比矩阵，如式（3）所示：

得到的方程F即为G（LX）的雅克比矩阵，则可知n维非线性方程组G（LX）=0，其修正方程为：

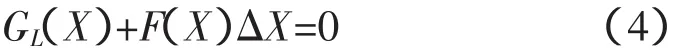
G（LX）的最小值方程可表示为：

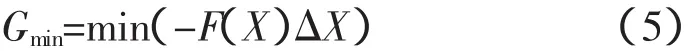
即使得G（LX）最小的rs、Xs、rr、Xr、rm、Xm和s等7个参数即为所需的辨识结果。式（5）将辨识负荷模型问题转变为求解非线性方程组的问题，应用基于二次插值的信赖域算法求解其最优解即可得到待辨识参数值。

2 基于信赖域的动态负荷参数辨识

2.1 信赖域算法基本原理

参数辨识问题是一种求解非线性优化问题，常用的求解非线性优化问题的算法有信赖域算法和线性搜索法。相比线性搜索法，信赖域算法思想新颖，可靠性高，具有较强的有效性和收敛性，故选择此算法应用于电力系统参数辨识。

信赖域算法的基本思想是基于迭代算法的，不同的在于每次迭代中给出一个信赖域，此信赖域通常是当前迭代点xk附近的一个领域，并在此领域内求解相应子问题，得到试探步长sk，然后应用某一种评价标准来评价这个试探步长是否合理并确定下一次迭代的信赖域[8-9]。如果合理则：

否则：

对于信赖域大小的选择，取决于试探步长的好坏，即如果试探步长好，则下一次迭代的信赖域相应扩大或保持不变，反之则减小。总体而言，信赖域算法的思想是通过每次对模型求解寻找试探步长，确定每一步的搜索方向，而不是传统的先确定搜索方向，再寻找试探步长[10]。

假设式（5）在当前点xk处有一微小领域，可定义为：

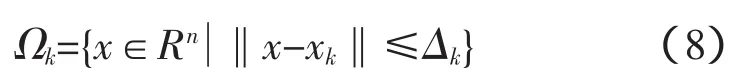
式中，Δk称之为信赖域，通常用信赖域半径来表示信赖域的大小。

由初值x0估计一个初始的信赖域半径，在这个领域内，目标函数在极值点附近可近似为一个二次函数[11]。本文中所讨论的为无约束最优化问题，因此可利用二次逼近，构造信赖域的子问题：

式中，s=x-xk；gk是目标函数 （f xk）在当前迭代点xk的梯度；Bk∈Rn×n对称，是 （f xk）在xk处Hesse矩阵的近似。假设式（9）的解为sk，则定义目标函数 （f xk）第k步真实下降量为：

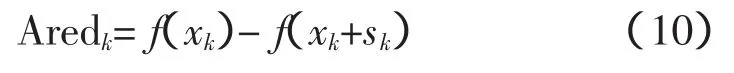
定义二次函数的预测下降量为：

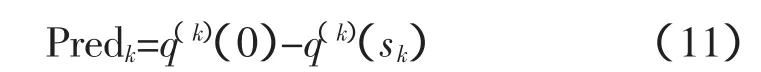
可得比值：

式（12）反应出二次函数的逼近目标函数的程度，即rk越接近1说明逼近程度越高[12]。利用rk作为确定信赖域的判据，当rk接近1时，说明二次函数逼近目标函数的程度良好，此时增大Δk，扩大信赖域。当rk∈（0，1）时，说明二次函数正在逼近目标函数，保持信赖域不变。当rk接近0时，减小Δk，缩小信赖域[13]。

2.2 基于信赖域的动态负荷参数辨识方法实现

根据基于二次插值信赖域算法流程，建立考虑机械暂态过程的动态负荷模型方程，由2.1节中提出的最小二乘法思想对动态负荷模型方程进行变换。通过提取系统运行时，动态负荷模型节点PMU数据，构建当前运行状态下如式（1） ～（5）所示的测量值与估测值之差的非线性方程组。

估测动态负荷模型各参数初始值，确定初始信赖域，进行动态负荷模型参数辨识，直至满足辨识终止条件，系统参数辨识终止，此时所得参数值即为辨识结果。参数辨识算法实现流程图如图2所示。

图2 信赖域算法流程图Fig.2 The flow chart of trust region algorithm

3 仿真算例与分析

本文使用Matlab/PSAT工具包，建立基于动态负荷模型的IEEE的3机9节点标准模型，用以验证由最小二乘法引导的信赖域算法辨识动态负荷模型参数的准确性。在Matlab/PSAT软件环境下建立如图3所示的IEEE的3机9节点标准模型。

分别在节点5、6、8上将PQ负荷模型替换为感应电机模型，作为系统的动态负荷模型。由于系统中同步电机及其AVR对系统电压起到一个维持和补偿作为，在仿真时间内其过程是一个动态变化的过程，故对于所建立的模型在考虑动态特性的情况下，可以进行参数辨识。仿真时间20 s，分别应用节点5、6、8的PMU数据，对其各节点等效动态负荷模型参数进行辨识。由于铁损的等值电阻和漏抗值相对于电力系统分析而言影响相对较小，在PSAT工具箱中感应电机模型参数未设定其铁损的等值电阻和漏抗。节点5、6、8动态负荷参数辨识结果如表1 ～表3所示。

表1 ～3分别表示实际参数与辨识结果对比结果，其误差相对较小，在可接受范围之内。图4 ～6分别表示在信赖域计算中每个收敛阶辨识结果与实际参数的差值，图中表明辨识过程约需要迭代10 ～15此即可得到辨识结果，收敛速度仍有待提高。由此可知信赖域算法应用于电力系统动态负荷主要参数的辨识是有效可行的。

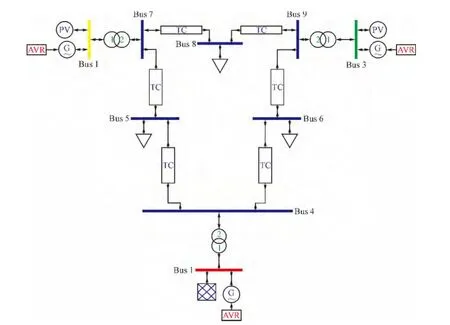
图3 IEEE3机9节点模型Fig.3 IEEE 3-machine 9-bus model

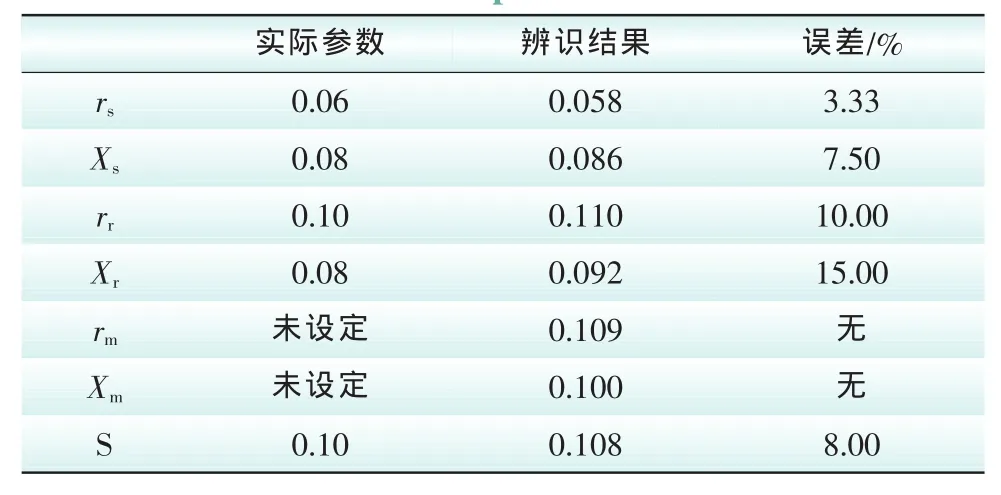
表1 节点8待辨识参数辨识结果Tab.1 The identification results of No.8 bus unknown parameters

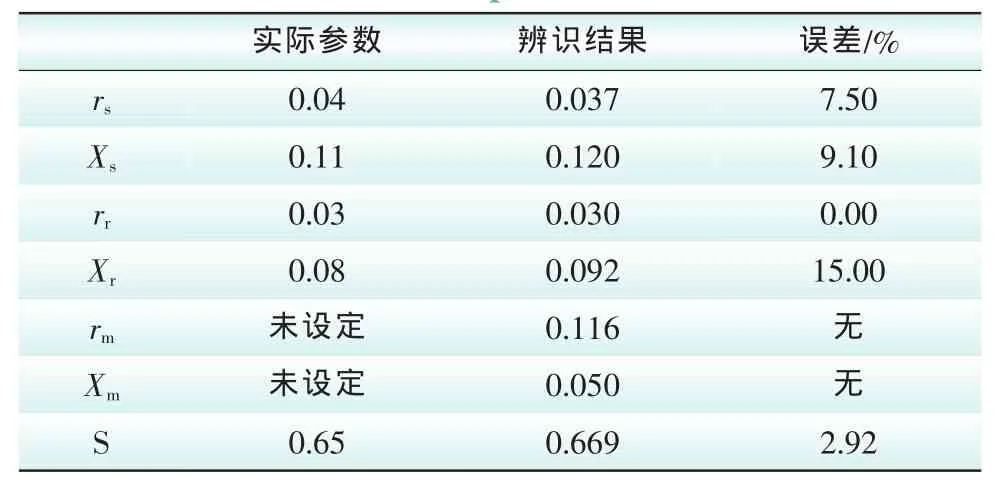
表2 节点5待辨识参数辨识结果Tab.2 The identification results of No.5 bus unknown parameters

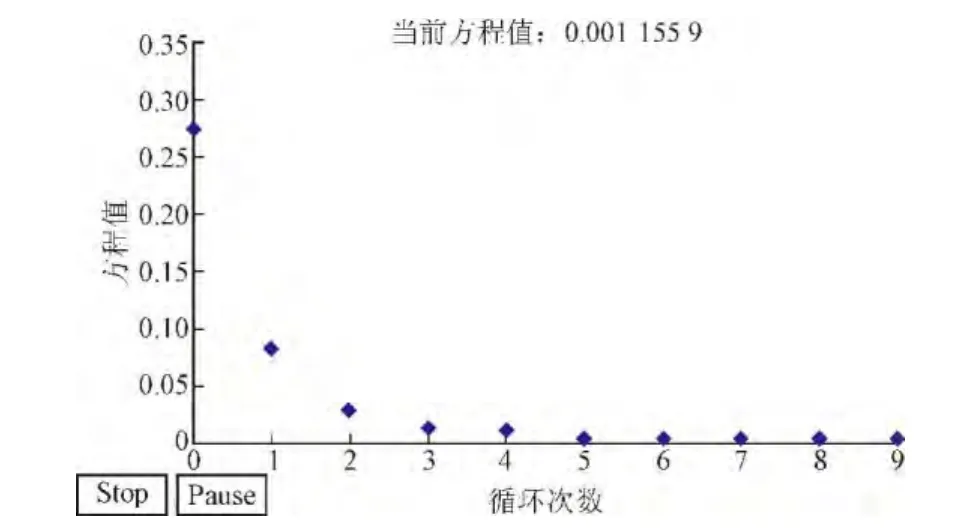
图4 节点8负荷辨识收敛阶与最小值关系Fig.4 Diagram of the m inimum and order of convergence for No.8 bus load identification

图5 节点5负荷辨识收敛阶与最小值关系Fig.5 Diagram of the m inimum and order of convergence for No.5bus load identification

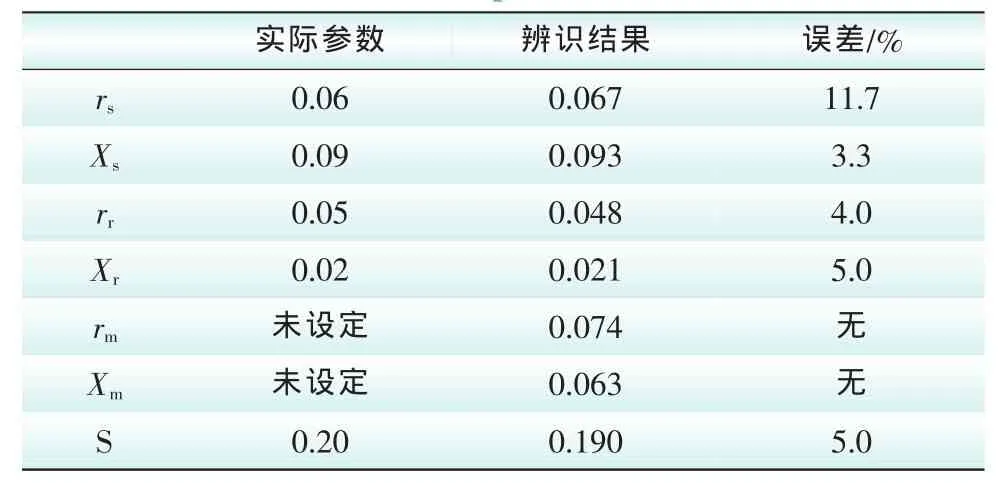
表3 节点6待辨识参数辨识结果Tab.3 The identification results of No.6 bus unknown parameters

图6 节点6负荷辨识收敛阶与最小值关系Fig.6 Diagram of the m inimum and order of convergence for No.6 bus load identification

4 结语

本文提出将信赖域算法应用于电力系统动态负荷参数辨识中。此方法以最小二乘算法思想为基础，能够将原本的参数辨识问题转化为求解非线性方程组最优解的问题，简化计算过程。仿真结果表明此算法有适应性强，不易陷入局部最优等优点，在电力系统辨识领域有广阔的应用前景[14-15]。

但由于算法本身的缺陷，运算实时性有待提高，同时，其适应于电力系统辨识的算法改进，如收敛判定、适应度函数等尚待进一步研究。

[1] 李颖，贺仁睦，徐衍会.广东电网基于PMU的负荷模型参数辨识研究[J].南方电网技术，2009，3（1）：16-19.LI Ying，HE Renmu，XU Yanhui.Research of PMU-based load model parameters identification of guangdong power grid[J].Southern Power System Technology，2009，3（1）：16-19（in Chinese）.

[2] 李涌.基于最小二乘法的汽轮机电液调节系统参数辨识[J].电力与能源，2013，34（1）：27-33.LI Yong.DEH system parameters identification based on the least squares method[J].Power and Energy，2013，34（1）：27-33（in Chinese）.

[3] 刘传铨，庄稼犁，田茜.供电线路事故特征的辨识及处理[J].电力与能源，2012，33（1）：27-30.LIU Chuangquan，ZHUANG Jiali，TIAN Xi.Supply lines accident identification method and treatment measures[J].Power and Energy，2012，33（1）：27-30（in Chinese）.

[4] 沈善德.电力系统参数辨识[M].北京：清华大学出版社.

[5] 陈宝林.最优化理论与算法[M].北京：清华大学出版社.

[6] 龚纯.精通MALAB最优化计算[M].北京：清华大学出版社.

[7] 王琳，马平.系统辨识方法综述[J].电力情报，2001（4）：63-65.WANG Lin，MA Ping.Review on methods of system identification[J].Information on Electric Power，2001（4）：63-65（in Chinese）.

[8] 张世华.信赖域算法中的若干调比技巧[D].石家庄：河北师范大学硕士论文，2006.

[9] 杨伟国，刘建.高压导电线路导线状态辨识研究[J].高压电器，2012，48（7）：62-65.YANG Weiguo， LIU Jian.Condition identification of highvoltage transmission lines[J].High Voltage Apparatus，2012， 48（7）： 62-65 （in Chinese）.

[10] 孙家南，赵洋，韦莉，等.基于系统辨识的电化学超级电容器建模[J].高压电器，2012，48（9）：16-21.SUN Jianan， ZHAO Yang， WEI Li， et al.Modeling of electrochemical super capacitor based on system identification[J].High Voltage Apparatus， 2012， 48（9）： 16-21 （in Chinese）.

[11] 赵菲，王铁强，贾京华，等.BPF法与PSO算法在励磁系统参数辨识中的应用[J].电力科学与工程，2011，27（11）:39-42.ZHAO Fei，WANG Tie qiang，JIA Jinghua，et al.Time domain parameters identification of generator excitation system based on WAMS[J].Electric Power Science and Engineering，2011，27（11）:39-42.

[12] 袁中琛，刘连光.变压器铁芯磁滞回线模型参数辨识[J].电网与清洁能源， 2010， 26（9）： 17-19.YUAN Zhongchen， LIU Lianguang.Identification of transformer core hysteresis loop model parameters[J].Power System and Clean Energy， 2010， 26（9）： 17-19 （in Chinese）.

[13] 陆进军，张力.基于PMU量测的线路参数辨识算法[J].电网与清洁能源，2012，28（11）：27-31.LU Jinjun， ZHANG Li.Line parameter identification algo-rithm based on PMU measurements[J].Power System and Clean Energy， 2012， 28（11）： 27-31 （in Chinese）.

[14] 刘晓倩，董新伟，杨瑞静.输电线路防雷措施的仿真与分析[J].电瓷避雷器，2012，135（4）：64-68.LIU Xiaoqian，DONG Xinwei，YANG Ruijing.Simulation and analysis on lightning protection measures of transmission lines[J].Insulators and Surge Arresters，2012，135（4）：64-68（in Chinese）.

[15] 曹海洋，王亮，朱启伟，等.MOA全电流在线监测实验平台设计与实现[J].电瓷避雷器，2012，135（4）：69-73.CAO Haiyang，WANG Liang，ZHU Qiwei，et al.MOA full current on-line testing platform design and implementation of experimental[J].Insulators and Surge Arresters，2012，135（4）：69-73（in Chinese）.