变电站应用大容量主变供电半径优化

王庆，秦旷宇，陈德伟

（1.国网山东省电力公司泰安供电公司，山东泰安 271000；2.上海市电力公司经济技术研究院，上海 200002）

变电站规划是配电网规划的核心和基础，其投资成本也在总成本中占较大比重。近期，上海市正着力推广远郊地区新建配网110 kV变电站应用大容量主变（63、80 MV·A）。这些地区通常供电面积大、负荷总量较小，故负荷密度较低，且主要集中在工业区、新城区和镇区，110 kV变电站采用大容量主变后，会导致10 kV电网的供电半径较长，供电电压质量的压力较大[1-4]。因此，如何确定变电站布点与容量，如何平衡主变容量释放与供电半径之间相对合理的关系，都是配网规划中需解决的核心问题[5]。

大容量变电站规划的主体部分包括变压台数、容量及供电半径的确定，是决定变电站投资成本及运行可靠性的重要因素。其关键在于建立一个合理有效的规划模型。

本文所建立的数学模型，可用于大容量主变变电站规划研究，考虑了适用于大容量主变的容载比约束，探讨了变压器容量、台数以及供电半径之间的关系，并寻求其最佳组合方案。

1 模型概述

本模型建立在总成本最小化的基础上。配网的投资运营成本包括：建设投资成本和每年的运行费用。

建模之前作以下假设[6-9]：

1）由一座位于区域中心的220 kV变电站向下级变电站供电。

2）中压配电网为辐射网络结构。

3）模型研究的对象是110/10 kV变电站，围绕220 kV变电站均匀分布。

4）规划目标区域内负荷均匀分布，每个110 kV变电站供电区域面积相等且为圆形，变电站处于圆心。

5）投资过程中不考虑资金的动态性，建设费用在规划期一次性投入。

6）负荷预测完全准确，年运行费用按当年实际负荷水平在年初一次性投入。

7）不考虑接线模式对进线平均长度的影响。

8）期末固定资产残值为零。

2 投资运行费用

2.1 配电网投资成本

配网建设投资总成本：

式中，Cb为变电站投资成本，万元；C、C为进、出线投资成本，万元。

2.1.1 变电站投资成本

假设变压器的台数为M，单台变压器容量为ΔS，则单个变电站的投资成本为：

式中，abo为变电站建设的固定成本，万元；ab为单台变压器的固定成本，万元；bb为与变压器容量相关的成本系数。

2.1.2 进线投资成本

假设变电站供电半径为l，进线平均长度L=l，系数β为曲折系数；若不考虑接线模式对进线长度的影响，可取β=2，则进线投资成本：

2.1.3 出线投资成本

假设每台变压器的出线为N为条，出线长度即为供电半径l，出线投资成本为：

式中，aLl为每条出线的固定成本，万元；b为单位长度出线投资成本，万元/km。

2.2 配电网运行成本

配网的年运行费用为：

式中，Fb为变电站运行费用，万元；Fl为线路运行费用，万元；Fw为设备维护费用，万元。

2.2.1 变电站运行费用

设变电站供电区域内的负荷密度为σ，则该区域内总负荷为PT=Aσ=πl2σ；每台变压器承担负荷为πl2σ/M，每条进线承担负荷为πl2σ/M，每条出线承担负荷为πl2σ/MN。

变压器运行时的电能损耗包括负载损耗与空载损耗，对应的实际运行费用分别为：

负载损耗

式中，ω为电价，元；ΔPd为变压器负载损耗，kW；cos φb为变压器功率因数；τ为最大负荷利用小时数。

空载损耗

式中，ω为电价，元；ΔPo为变压器空载损耗，kW；T为变压器运行的时间，这里取一年，即T=8760 h。

变压器总运行费用

2.2.2 线路运行费用

线路运行费用即进出线损耗所产生的费用，它由进出线的电流密度、单位电阻等因素决定。

进线运行费用：

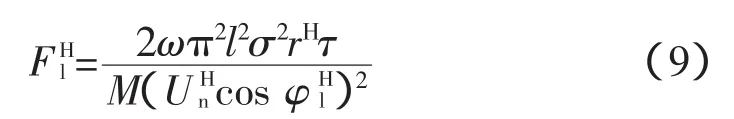
式中，ω为电价，元；l为变电站供电半径；σ为负荷密度，MW/km2；U为进线电压等级；rH为进线单位等效电阻；cos φ为进线功率因数。

出线运行费用：

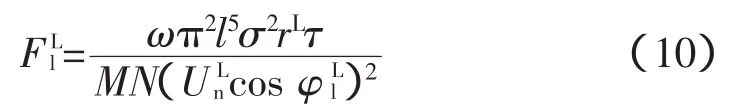
线路总的运行费用为：

2.2.3 设备维护费

设备维护费为配网运行费用中的固定费用，一般取投资成本的某一比例，表示为：

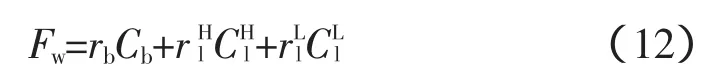
式中，Cb、C、C为变电站及进出线投资成本，万元；、为变电站及进出线维护率。

3 优化模型

3.1 目标函数

由于规划期内配网运营的收入流取决于规划区域实际负荷需求，与变压器的容量、台数和供电半径均无关，且期末固定资产残值为零，故将最小化总成本作为优化目标；实际目标函数为所有投资成本与运行费用的现值。

设目标规划区域的面积为A，则区域内变电所数量为：

符号「·骎表示取整运算。

规划总成本的现值为：

式中，i为贴现率（此处可取电力工业平均收益率）；n为规划期年数；（P/F，i，n）为现值系数，计算如下：

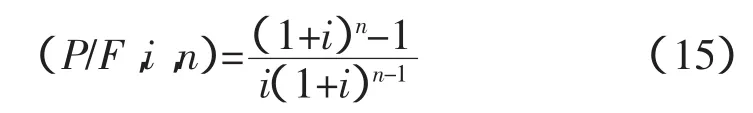
3.2 约束条件

目标函数需要满足以下约束条件：

“N-1”约束即其中一台变压器因故障退出运行，其余变压器承担全部负荷而不过载[10-12]，此时变压器容量和台数应满足下式

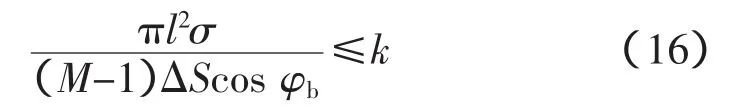
式中，k为变压器短时允许过载率。k值有2种定义方式，一种是根据变压器绝缘老化定理，允许变压器短时间（一般为2 h）过负荷而不会影响变压器的使用寿命，此时k=1.3；一种是根据变电所中任一台变压器因故障停运时，剩余变压器承担全部负荷而不过载来定义，此时k=1。

容载比约束

容载比要求满足

式中，Rsmin、Rsmax分别为110 kV配电网容载比的最小值和最大值。应用110 kV大容量主变后，10 kV配电网的容载比范围可取1.9 ～2.1。

综上，完整的优化模型为

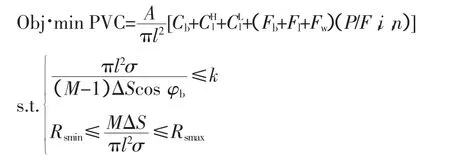
对此优化模型的求解，可通过对目标函数分别对主变容量、台数、供电半径求导，并令其等于零即可得到。

4 算例分析

110/10 kV变电站目前容量以40 MV·A为主，为节约占地面积等，以上海某地区应用大容量主变为例，对大容量主变应用后变电站的最优供电半径进行研究。

上海某地区供电面积为26.62 km2，计划2 a内新建110/10 kV变电站应用大容量主变，主变容量为80 MV·A，台数为2台。80 MV·A主变和进、出线基本参数，如表1所示。进线选用截面积为800 mm2电缆，出线选用截面积为3×400 mm2的电缆。

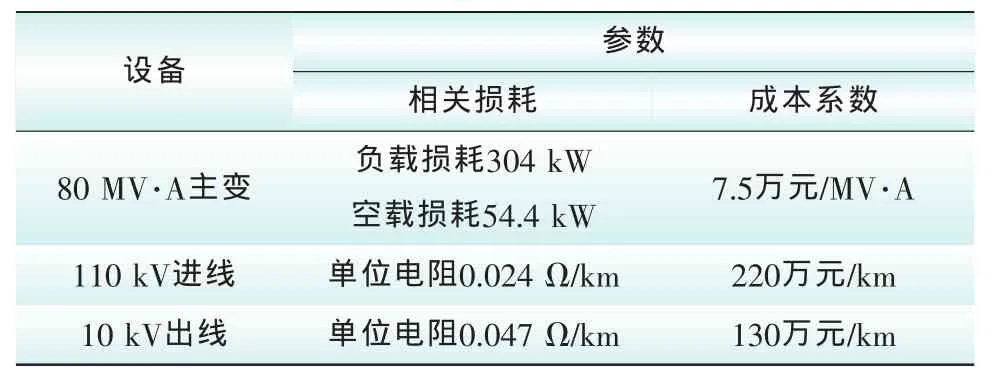
表1 80 MV·A主变和进、出线基本参数Tab.1 The 80 MV·A transformers and its basic inlet，outlet parameters

每座变电站本体及其他设备投资成本为150万元，单台变压器的固定成本为20万元，每条进线固定成本为80万元，每条出线固定成本为45万元。变压器的功率因数为0.95，进出线的功率因数为0.9，所有设备每年的维护费均取其投资额的3.2%，最大负荷利用小时数为5700 h，平均电价为0.52元/kW·h，电力工业平均收益率8%，变压器短时容许过载率为1.3，容载比范围1.9 ～2.1。

根据变电站供电半径优化模型，代入上述各个参数，并对供电半径求导，可得不同负荷密度对应的最优供电半径，以及所需建设的大容量变电站个数。其中，以负荷密度为30 MW/km2为例，总成本现值和供电半径之间的关系如图1所示，可见，对于一定的负荷密度，一定存在一个使总成本最小的最优供电半径。

图1 投资总成本与供电半径关系图Fig.1 Relationship between the total investment cost and power supp ly radius

不同负荷密度对应的最优供电半径，以及所需建设的大容量变电站个数的计算结果见表2。

表2 80 M V·A主变对应的参数结果Tab.2 Parameters corresponding to the 80 MV·A transformer

根据表2的计算结果可知，负荷密度小于3 MW/km2时，供电半径超过2 km；负荷密度小于10 MW/km2时，供电半径超过1.5 km。随着负荷密度的升高，变电站供电半径逐渐变小，所需变电站数目和费用增加。

同时将计算结果与该地区规划情况相对比，该区计划新建1座2×80 MV·A的110 kV变电站，10 kV及以下总负荷约为81.31MW，负荷密度约为3.1 MW/km2，与该模型的计算值相同，验证了模型的正确性。

对该地区来说，新建的110 kV大容量变电站，不仅给区内近期新增负荷提供了电源，同时取代了容量较小的35 kV变电站，且与该地区其他小容量110 kV变电站形成联络，为本地区的发展做出贡献。

若该区新建的110 kV变电站主变容量是50MV·A，根据上述变电站供电半径优化模型，计算应用50 MV·A主变时的最优供电半径及变电站数目和规划总成本。其中，50 MV·A主变参数，如表3所示，进线选用截面积为630 mm2的电缆，出线选用截面积为3×400 mm2的电缆。

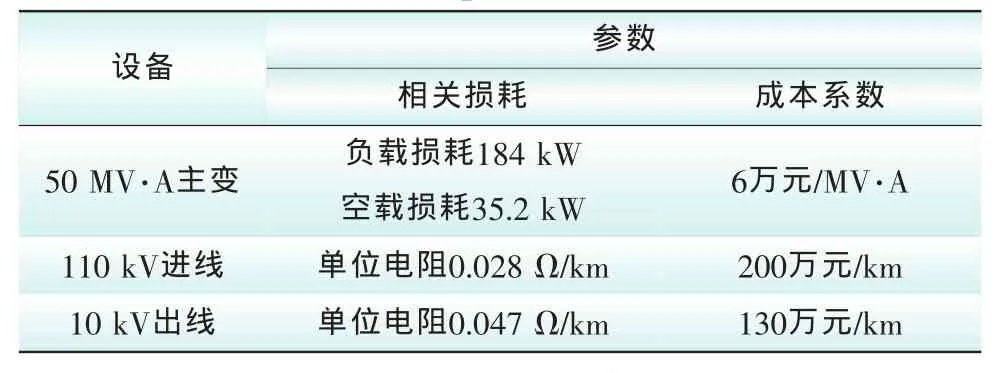
表3 50 MV·A主变和进、出线基本参数Tab.3 The 50 MV·A transformers and its basic inlet，outlet parameters

每座变电站本体及其他设备投资成本为130万元，单台变压器的固定成本为15万元，每条进线固定成本为80万元，每条出线固定成本为45万元。其他参数不变。

经计算，主变容量为50 MV·A时，不同负荷密度对应的最优供电半径以及所需建设的大容量变电站个数的计算结果，如表4所示。

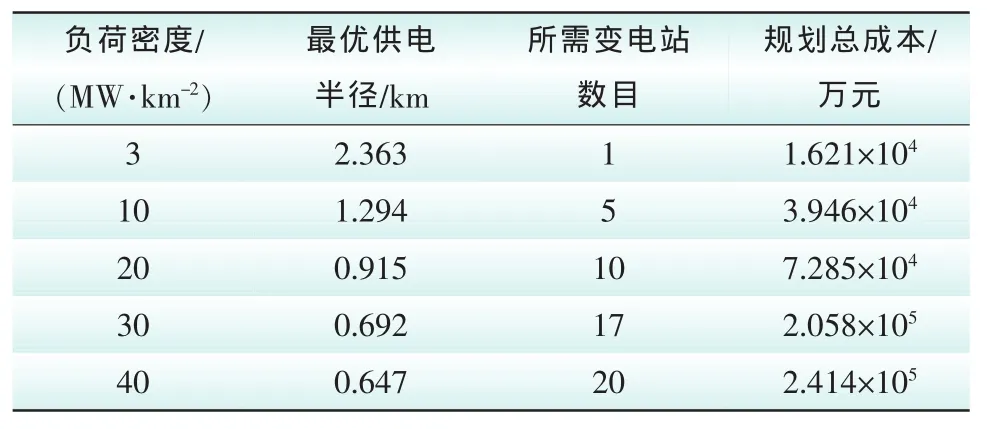
表4 50 M V·A主变对应的参数结果Tab.4 Parameters corresponding to the 50 MV·A transformer

由表2和表4的计算数据，可得出图2和图3。主变关于供电半径和变电站个数的图形比较，如图2、图3所示。

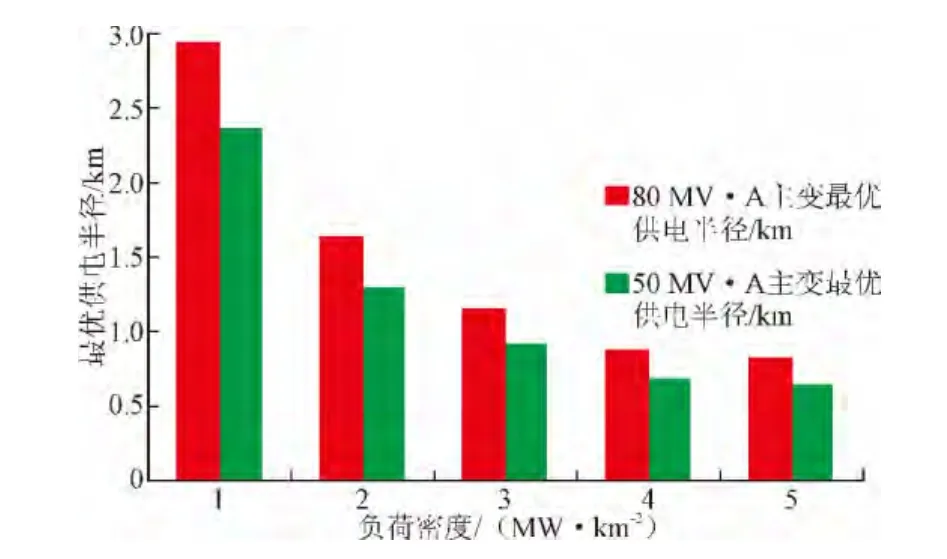
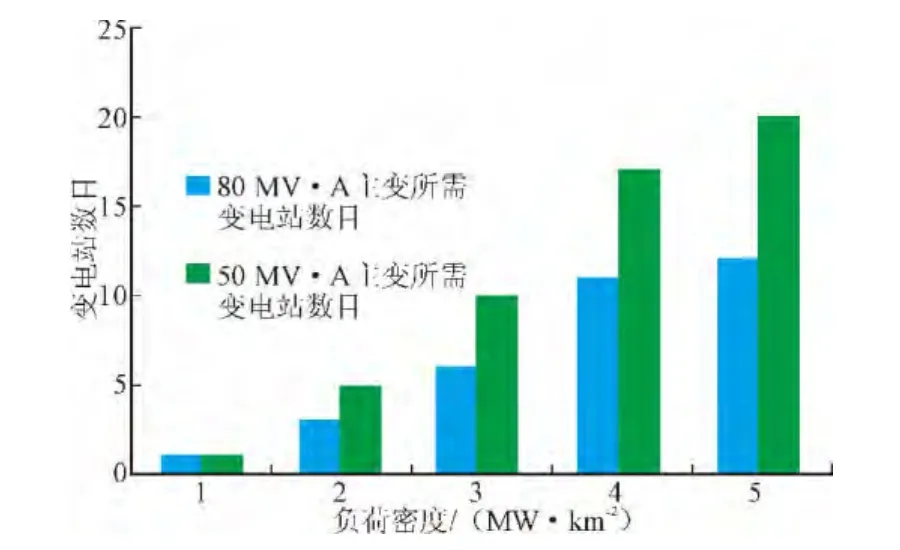
图3 不同容量主变对应的变电站个数图Fig.3 Number of substations corresponding to transformers of different capacities

从图2、图3可知，当变电站用50 MV·A主变时，变电站的最优供电半径较80 MV·A主变时有所减小，所需变电站数目有所增加，规划总成本增加。供相同大小负荷，应用大容量主变所需的变电站数目较少，节省了占地资源。且当供电区负荷密度高于20 MW/km2时，建设大容量变电站比建设相对小容量变电站的费用少，具有一定的经济效益。

5 结论

本文提出的变电站规划模型可用于求解变电站应用大容量主变后的最优供电半径，同时也可求主变容量和台数。利用该模型对上海某地区的大容量变电站进行规划，可得出该变电站的最优供电半径及所需变电站数目和规划期总投资费用。从计算结果可以看出，随着地区的发展，负荷密度逐渐提高，变电站的最优供电半径变小，设备运行费用提高，所需变电站的个数也随之增多。

与建设较小容量变电站相比，110 kV变电站应用较大容量主变可减少变电站建设数目，减少变电站建设投资，具有一定的经济效益。但是大容量主变应用后，中压网相关配置也会随之改变，经济效益需进一步分析，此处不考虑中压网投资建设费用。

[1] 王璞，王承民，张焰，等.城市配电网规划中变电站最佳供电半径及容量的实用计算方法[J].电气应用，2011，30（23）：38-41.WANG Pu，WANG Chengmin，ZHANG Yan，et al.Practical calculation method of the optimal power substation radius and capacity of urban distribution network planning[J].Power Distribution，2011，30（23）:38-41（in Chinese）.

[2] 肖萍，周新军，汪沨，等.基于先导闪络判据的变电站侵入波过电压的研究[J].电瓷避雷器，2013（1）：16-20.XIAO Ping，ZHOU Xinjun，WANG Feng，et al.Study of the lightning invaded overvoltage in substation based on leader flashover criterion[J].Insulators and Surge Arresters，2013（1）：16-20.

[3] 杨丽徙，贾德峰，任群，等.数据融合技术在变电站选址中的应用[J].电力自动化设备，2003，23（8）：57-59.YANG Lixi，JIA Defeng，REN Qun，et al.The application of data fusion technology in the transformer substation locations[J].Electric Power Automation Equipment，2003，23（8）:57-59（in Chinese）.

[4] 牛卫平，刘自发，张建华，等.基于GIS和微分进化算法的变电站选址及定容[J].电力系统自动化，2007，31（18）：82-86.NIU Weiping，LIU Zifa，ZHANG Jianhua，et al.Substation locating and sizing based on GIS and differential evolution algorithm[J].Automation of Electric Power Systems，2007，31（18）:82-86（in Chinese）.

[5] 李公波，徐刚，沈杨.变压器循环电流对无功自动补偿装置测量的影响[J].电力电容器与无功补偿，2012，33（6）：30-32.LI Gongbo，XU Gang，SHEN Yang.Influence of transformer circulating current on reactive power automatic compensation device[J].Power Capacitor&Reactive Power Compensation，2012，33（6）:30-32（in Chinese）.

[6] 王成山，魏海洋，肖峻，等.变电站选址定容两阶段优化规划方法[J].电力系统自动化，2005，29（4）：62-66.WANG Chengshan，WEI Haiyang，XIAO Jun，et al.A two-stage optimal planning method for substation locating and sizing[J].Automation of Electric Power Systems，2005，29（4）:62-66（in Chinese）.

[7] 顾洁，陈章潮，张焰，等.城市电网变压器负载率取值研究[J].电力系统及其自动化学报，1995，7（4）：26-32.GU Jie，CHEN Zhangchao，ZHANG Yan，et al.The value ranging study of urban power transformer load rate[J].Proceedings of the CSU-EPSA，1995，7（4）:26-32（in Chinese）.

[8] 刘友强，李欣然.变电站经济容量和经济供电半径的探讨[J].广东电力，2005，18（11）：7-9.LIU Youqiang，LI Xinran.Discussion on economical capacity and economical power supply radius for transformer substations[J].Guang Dong Electric Power，2005，18（11）:7-9（in Chinese）.

[9] 朱立蓉，王璞，王承民，等.配电网规划中电压等级的优化选择方法研究[J].电网与清洁能源，2010，26（11）：16-18.ZHU Lirong，WANG Pu，WANG Chengmin，et al.Optimal selection method of voltage level in power distribution network planning study[J].Power System and Clean Energy，2010，11（26）:16-18（in Chinese）.

[10] 厉达，程浩忠，俞国勤，等.变电站的经济容量优化模型及其不同负荷密度下的变压器配置研究[J].电力系统保护与控制，2009，37（19）：5-9.LI Da，CHENG Haozhong，YU Guoqin，et al.Optimum model for substation’s economical capacity and the configuration of transformer under different load density[J].Power System Protection and Control，2009，37（19）:5-9（in Chinese）.

[11] 魏凯鸿.基于变电站容量与供电半径经济性的数学模型建立[J].动力与电气工程科技资讯，2008（30）：109-111.WEI Kaihong.Based on the substation capacity and the economical power supply radius established mathematical model[J].Automation of Electric Motivation and Electrical Engineering Science and Technology Information，2008（30）:109-111（in Chinese）.

[12] 曹静，王五一.500 kV主变保护与其他关联回路的简要分析[J].电力科学与工程，2009，25（12）:49-52.CAO Jing，WANG Wuyi.Analysis of 500 kV main trans for merprotection and other related loop[J].Electric Power Science and Engineering，2012，28（11）:28-31.