板模型中带周期边界条件的迁移算子的谱分布
2014-05-11
(上饶师范学院,江西 上饶 334001)
1 相关知识
二十世纪五十年代,文献[1]对无限平行板几何提出了最具一般的中子迁移方程:
该迁移方程解的渐近性态和该迁移算子的谱分析研究已成为数学和物理等众多科学领域感兴趣的课题(部分参见文献[5-8]). Khalid Latrach 等人在文献[2]中研究了一类带周期和完全反射边界条件粒子单能的迁移方程,证明了迁移算子产生C0半群,证明了该C0半群产生的Dyson-Phillips展开式的二阶余项是紧和弱紧性。王胜华等人在文献[3]中对L2空间板几何中带周期边界条件连续能量的迁移方程进行研究,证明了这类迁移算子产生C0半群V(t)(t≥0)以及该半群产生的二阶余项是紧的,得到了该迁移算子的谱分析等结果。文献[4]又将文献[3]的部分条件做了推广,其中边界条件推到广义边界条件:
ψ(-a,v,μ)=αψ(a,v,μ),0<μ<1;ψ(a,v,μ)=αψ(-a,v,μ),-1<μ<0;0≤α<1
注意到,文献[4]中的α∈〔0,1),显然当α=1时,结果又将如何?引起了我们的关注。本文对板模型中一类带周期边界条件下非均匀介质的迁移方程进行研究,证明了这类迁移算子AH产生C0半群V(t)(t≥0),证明了该半群产生的Dyson-Phillips展开式的二阶余项的紧和弱紧性,最后得到了文献[4]的结果。下面研究一类带周期边界条件下非均匀介质的初边值问题:
其中H平行板的左右面上的周期算子。即,

(1.1)
其余符号意义见文献[4,7]。
令Xp=Lp(D=〔-a,a〕×E×〔-1,1〕)(1≤p<∞)表按通常范数构成的Banach空间,在Xp上定义streaming算子:
令σ0=ess-inf{σ(x,v)}。对φ∈Xp,考虑方程
(λ-B)ψ=φ
则对任何Reλ>-σ0,当μ∈〔-1,1〕时有
(1.2)
由半群的性质和(1.2)式可得,算子BH在Xp上生成C0半群U(t)(t≥0)的表达式为:
引理1.1[3]设H为(1.1)式中所确定的周期边界算子,那么迁移算子AH在Xp空间上生成C0半群(V(t)(t≥0),而且
当n=2时,显然可以得到二阶余项为:

(1.3)
2 主要结果
假设(O):K为正则算子,即K限制在Lp(D)上是紧正算子。不妨假设K为秩一算子,并且仍用K表示。那么
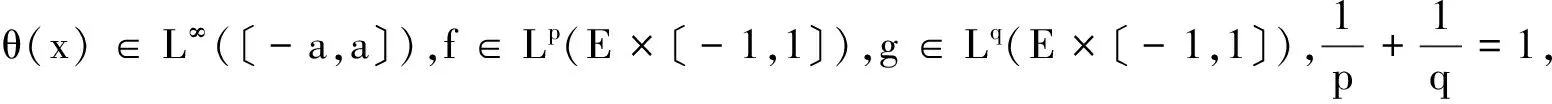
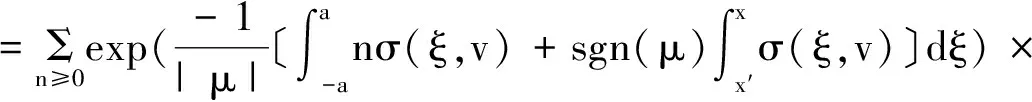
φ(2na sgn(μ)-μt2+x,v′,μ′)χ〔((2n-1)a+sgn(μ)x)/|μ|,((2n+1)a+sgn(μ)x)/|μ|〕(t2)

由引理1.1可令:
(2.1)
f(v′,μ′)g(v″,μ″)dμ″(V(t-t1-t2)φ)(2ka sgn(μ)-μt1+x1,v″,μ″)×
χ〔((2n-1)a+sgn(μ′)x1)/|μ′|,((2n+1)a+sgn(μ′)x1)/|μ′|〕(t2)χ〔((2k-1)a+sgn(μ)x)/|μ|,((2k+1)a+sgn(μ)x)/|μ|〕(t1).
令Γ=σ(AH)∩{λ∈C|Reλ>ω},其中ω>e是(U(t)(t≥0)本质谱型)。
定理2.1 若假设条件(O)被满足,则迁移算子AH的谱在区域Γ中仅由有限个具有限代数重数的离散本征值所组成。
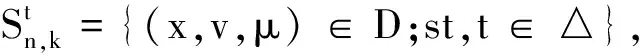
由于对任意固定的t>0 ,必∃k0(t)∈Z,使得当k≥k0(t)时有:
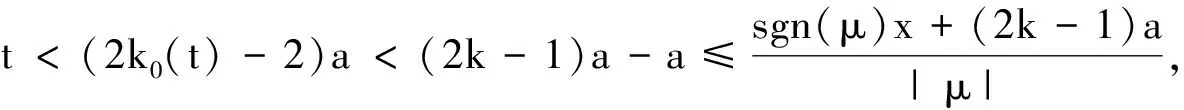
于是(2.1)可表示为:
f(v′,μ′)g(v″,μ″)dμ″(V(t-t1-t2)φ)(2ka sgn(μ)-μt1+x1,v″,μ″)×
χ〔((2n-1)a+sgn(μ′)x1)/|μ′|,((2n+1)a+sgn(μ′)x1)/|μ′|〕(t2)χ〔((2k-1)a+sgn(μ)x)/|μ|,((2k+1)a+sgn(μ)x)/|μ|〕(t1),
f(v′,μ′)g(v″,μ″)dμ″(V(t-t1-t2)φ)(2ka sgn(μ)-μt1+x1,v″,μ″)×
χ〔((2n-1)a+sgn(μ′)x1)/|μ′|,((2n+1)a+sgn(μ′)x1)/|μ′|〕(t2)χ〔((2k-1)a+sgn(μ)x)/|μ|,((2k+1)a+sgn(μ)x)/|μ|〕(t1).

Tε={(t1,t2)∈R2,t1≥0,t2≥ε>0,t1+t2≤t},
于是可得
θ(2ka sgn(μ)-μ′(t1,t2,x,x0,μ)t1+x1)(V(t-t1-t2)φ)(t1,t2,x0,v″,μ″)×
χ〔((2n-1)a+(2na-μ′(t1,t2,x,x0,μ)t2+x))/|μ′(t1,t2,x,x0,μ)|,((2n+1)a+(2na-μ′(t1,t2,x,x0,μ)t2+x))/|μ′(t1,t2,x,x0,μ)|〕(t2)×
χ〔((2k-1)a+sgn(μ)x)/|μ|,((2k+1)a+sgn(μ)x)/|μ|〕(t1).
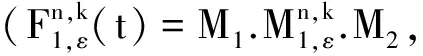
M1:Xp→Lp(Tε×D),M1φ(t1,t2,x,v,μ)=(V((t-t1,t2)φ)(x,v,μ);

χ〔((2n-1)a+(2na-μ′(t1,t2,x,x0,μ)t2+x))/|μ(t1,t2,x,x0,μ)|,((2n+1)a+(2na-μ′(t1,t2,x,x0,μ)t2+x))/|μ(t1,t2,x,x0,μ)|〕(t2)×
χ〔((2k-1)a+sgn(μ)x)/|μ|,((2k+1)a+sgn(μ)x)/|μ|〕(t1).

其中D0=E×〔-1,1〕,M为常数。下面延拓h(.,.)使得它在E×〔-1,1〕外为0,延拓φ(.,.,.,.)使得它在Tε×〔-a,a〕×E外也为0,则



参考文献:
[1] Lehner.J and Wing.G.M.Solution of the linearized Boltzmann equation for the slap geometry[J]. Duke.Mate,1956,23:125-142.
[2] Khalid Latrach and Abdelkader Dehici. Spectral properties and time asymptotic behaviour of linear transport equations in slab geometry[J].Mathematical Methods in the Applied Sciences,2001,24: 689-711.
[3] 王胜华,贾善德. 板几何中一类具周边条件迁移算子的谱[J].西南师范大学学报,2005,30(6):964-970.
[4] 吴红星,王胜华.板几何中具广义边界条件的迁移算子的谱[J].南昌大学学报(理科版),2009,33(5):415-420.
[5] Wang Shenghua,Yang Mingzhu,Xu Genqi. The spectrum of the transport operator with generalized boundary conditions[J].Transport Theory and Statistical Physics,1996,25 (7):811-823.
[6] 吴红星,王胜华,袁邓彬.一类具抽象边界条件的迁移算子的谱分布[J].纯粹数学与应用数学,2013,29(5):489-497.
[7] 吴红星,王胜华,袁邓彬. 紧性在迁移方程中的应用[J].数学的实践与认识,2013,43(22):166-173.
[8] Voigt J. Spectral properties of the neutron transport Equation[J].Journal of Mathematical Analysis and Applications ,1985,106:140-153..
[9] 曹玉平.基于高职数学分层教学的实验研究[J].职教论坛,2013,(2):35-37.
