一种改进的多假设跟踪算法

蒋富勤 朱鲲 祝献

（第七一五研究所 声纳技术重点实验室，杭州，310012）

在目标检测中，提高门限，可以降低虚警，但同时也降低了检测概率，影响目标检测，尤其是弱目标检测。事实上，对于虚警，可以通过后续观察予以剔除。因此，在目标检测过程中，适当降低门限，提高检测概率，允许一定的虚警概率，通过后续观察数据来辨识哪些是目标，哪些是虚警，哪些出现漏报。

在检测概率小于1和存在虚警或杂波情况下的目标跟踪，其主要难点在于数据关联。目前，已发展了许多方法试图解决这一问题。两种简单的方法是强近邻方法（SN）[1]和最近邻方法（NN）[2]。SN 关联跟踪门内最强的测量。NN则关联跟踪门内与预测值最接近的测量。随着虚警概率的增加，这两种方法无法实现目标跟踪。概率数据关联（PDA）[3]则选用跟踪门内所有测量，而不是其中一个，赋予它们不同的概率。在多目标情况下，除了测量与测量之间存在竞争外，测量还可能位于多个目标的跟踪门内，数据关联与跟踪变得更为困难。其它方法还有全局最近邻方法（GNN）、联合概率数据关联（JPDA）[4]、多假设跟踪（MHT）[5]、概率多假设跟踪（PMHT）[6]，维特比数据关联（VDA）[7]等。

1979年，Reid在0-1整数规划方法基础上，结合全邻最优滤波器和Bar-Shalom的聚概念，提出了多假设跟踪方法。MHT建立多个候选假设，通过后续观察数据进行延迟关联判决，但假设数目随目标个数和虚警个数的增加呈指数级增加，需要对假设进行修剪，删除低概率的假设，维持适度规模的假设数目。这也是MHT实现工程化应用的关键步骤。

维特比算法在通信和语音识别中广泛使用，它在离散马尔科夫系统中是最佳的。在数据关联中，维特比算法同样得到应用。VDA的关键思想是基于测量而不是离散状态集创建网格图。网格上的路径对应一个数据关联序列。维特比算法可确定网格上的最小代价路径。本文结合MHT和VDA的思想，提出了一种改进的多假设跟踪算法。降低计算复杂度，实现快速目标关联与跟踪。

1 状态-空间模型

对于单阵多目标数据关联和跟踪问题，为简单起见，这里假设目标个数为T，且目标相互独立，不机动。那么多目标跟踪系统模型可用状态-空间模型表示：

其中i= 1,2,… ,T，xi(k)是k时刻第i个目标的状态向量，F(k)是已知的状态转移矩阵，vi(k)和wi(k)是独立同分布的零均值白高斯噪声，yj(k)是目标测量，H(k)是测量矩阵。目标和测量之间的对应关系i↔j未知。在测量过程中，目标可能存在漏报和虚警。虚警采用PDA均匀/泊松模型，即虚警测量值在测量空间内服从均匀分布，虚警个数服从泊松分布，其参数为λ。

2 算法原理

2.1 多假设跟踪算法

NN是最简单的关联算法，它关联跟踪门内与预测值最接近的测量，其计算公式如下：

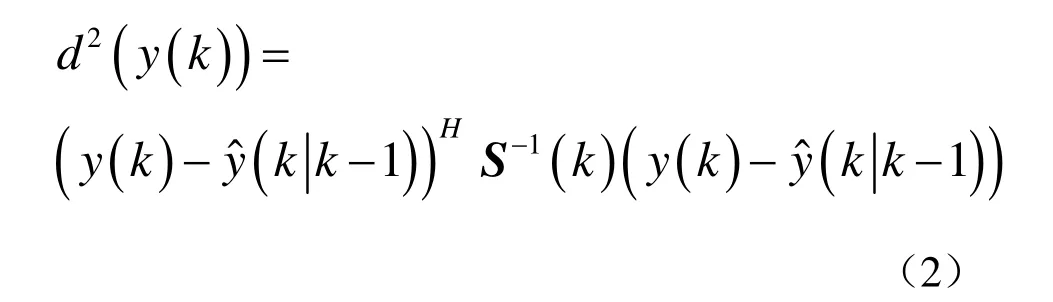
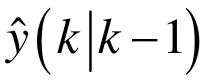
MHT正是基于延迟判决的思想发展而来的。它认为每个新接收到的测量可能源于新目标、虚警或已知目标，它通过一个有限长度的时间滑窗，建立多个候选假设，通过数据聚类、假设生成、假设删除、假设矩阵管理等步骤实现数据关联和目标跟踪。由于假设数目随目标个数和虚警个数的增加呈指数级增加，需要对假设进行修剪，删除低概率的假设，如 m-最优MHT算法。

m-最优MHT算法的核心思想是通过Murty算法搜索前m个最优解，即删除各时刻低概率假设，保留前m个最优假设，抑制假设个数的急剧增加。这种算法虽然可以缓解计算量的指数级增长，但当目标个数和虚警数目较多时，Murty算法搜索最优m个解依然需要较长时间，需要进一步优化。

2.2 维特比数据关联算法

VDA 算法[7]是在网格图中搜索数据关联kΘ中最有可能的序列：

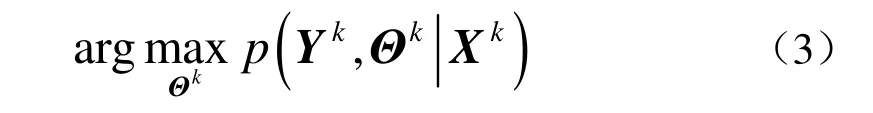
其中，Xk、Yk分别是1～k时刻的状态序列和测量序列。

关于测量序列和关联事件序列的联合概率密度可分解为

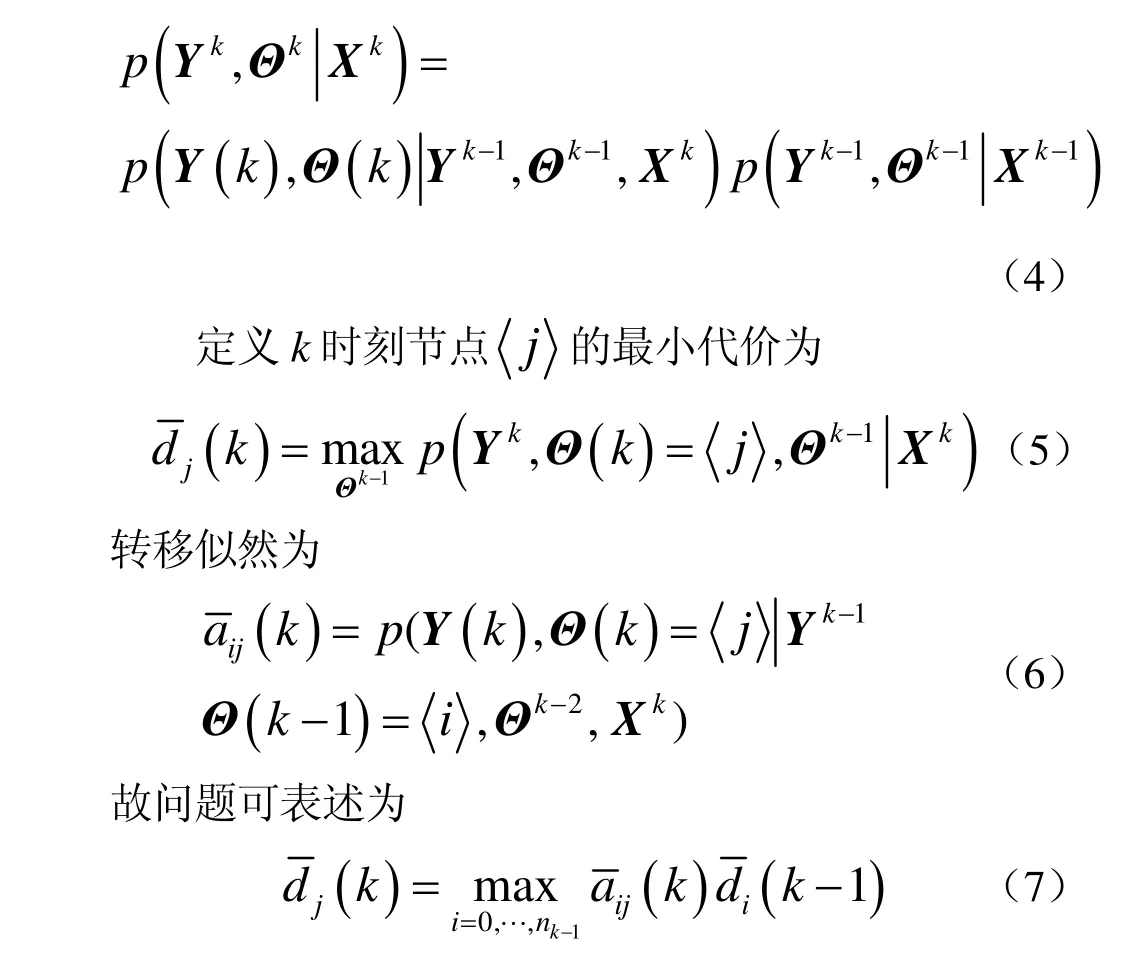
其中j= 0 ,… ,nk，nk是k时刻时网格图的节点个数，其与测量个数有关。对代价取负对数，问题可转化为搜索最小代价路径问题：

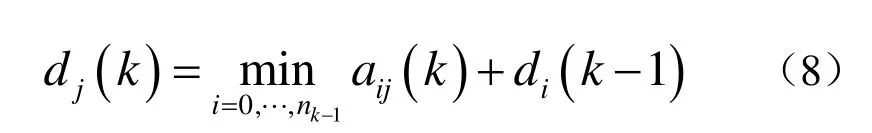
2.3 改进的多假设跟踪算法

为减少MHT计算量，需要对假设生成和假设删除等进行优化。这里，通过网格图减少假设数目，删除低概率假设，实现快速目标关联跟踪。每个新接收到的测量可能源于新目标、虚警或已知目标，同时考虑这3种情况计算复杂。这里对于目标的关联跟踪分成两步。

2.3.1 关联跟踪已知目标。

对于已知目标而言，新目标和虚警测量都是错误关联的测量，均可视为虚警。因此，测量假设分为两种情况：源于已知目标、源于虚警和新目标。

图1表示k-1时刻到k时刻的网格图。每个节点包含目标编号、当前时刻目标状态和协方差矩阵、路径代价，以及指向前一时刻的节点位置。图1(a)表示位于门限范围以内的路径；通过比较节点上各路径的代价，图1(b)给出了各节点选择的幸存路径。从图中可以看出，k时刻节点3没有与k-1时刻的节点关联，认为其为虚警。k时刻节点1和节点2均与k-1时刻节点1关联，路径出现分支，需要通过后续观察数据确定哪一条是真实路径。k-1时刻节点2没有与后续节点关联，该路径终止，停止跟踪。如果它是分支路径之一，认为其不是真实路径。但实际上检测概率不为1，会出现漏报，为此k时刻设置新的节点，关联k-1时刻未被关联的路径节点2，节点状态采用预测值。若这条路径不是真实路径，其后续路径多采用预测值，而不是测量值与之关联。在一定长度时间窗内，当采用预测值次数或代价大于某个门限时，停止跟踪，修剪这条分支路径，释放分支期间关联的测量数据。

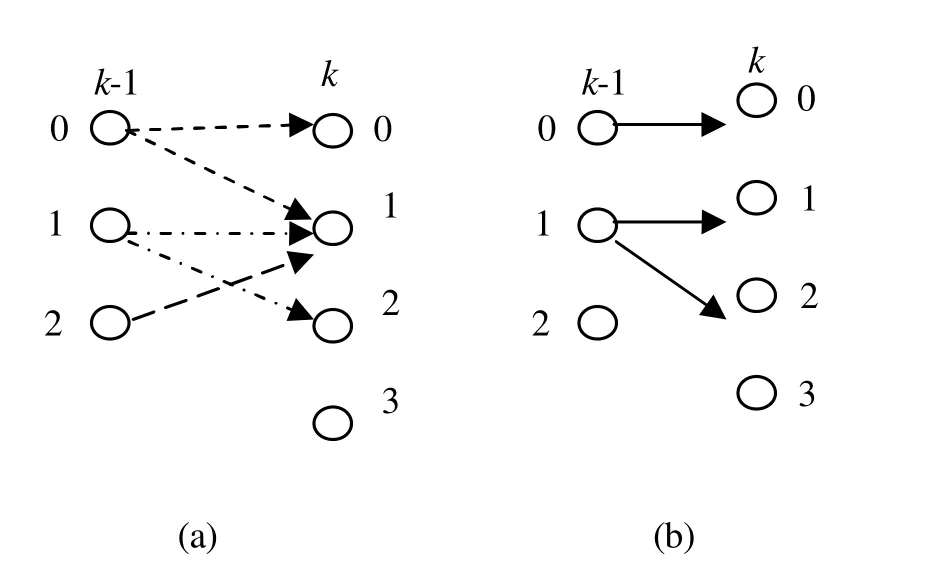
图1 网格图

2.3.2 新目标初始化

测量假设分为两种情况：潜在的新目标和虚警。在k-p时刻，若存在m个未关联的测量数据（即认为是虚警的测量和被修剪的分支测量），假定其为潜在的新目标Newi,i= 1 ,… ,m，重复第一步的过程，其中关联的数据为k-p～k时刻未关联的测量数据。到k时刻时，若某个潜在目标路径上关联的测量数据个数大于某个门限（如Pd*（p+1）,其中Pd为检测概率），则认为该目标为新目标，否则认为是虚警。

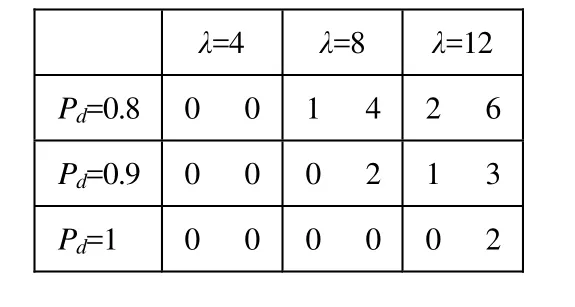
在目标跟踪过程中，设置计数器q，q

若目标1和目标2在跟踪过程中出现交叉，有时会出现交叉之后，1）交叉后目标1路径分配给目标2，目标2路径分配给目标1，称之为交叉交换；2）交叉之后的两条路径均分配给同一个目标，造成另一个目标失跟。为此，若目标间距离小于某个门限值，认为其可能会出现交叉，对其进行数据关联时应考虑：1）门限内存在多个测量时，每个目标至少分配一个节点，避免目标失跟；2）根据一段时间的目标路径数据进行曲线拟合，预测当前时刻测量值，而不是采用一步预测值。在这两个原则基础上选择使代价最小的数据关联方案。

3 仿真结果

仿真中，共有6个目标，测量数据为目标方位，其方位标准差σ为0.5º，检测概率Pd为0.8，虚警值服从均匀分布，其个数服从泊松分布，参数λ取4和8。改进的MHT算法结果见图2。

图2 多目标关联跟踪结果

图2（a）和（c）是λ取4和8时的测量数据，图 2（b）和（d）为相应的关联跟踪结果，不同颜色代表不同目标的关联跟踪结果。从图中可以看出，改进的MHT算法可以实现虚警环境下的多目标关联与跟踪。

在个人计算机上，采用 m-最优 MHT算法（m=2，延迟判决长度N=5）时，完成上述6个目标的跟踪（λ=4）需要845 s，不使用新目标初始化功能时需要31.5 s；而相同情况下，采用改进的MHT算法前者只需2.9 s，后者只需1.5 s，运算速度得到大幅提高。

假定跟踪后得到的方位值与真实值相差 1°以内，则认为该时刻检测到目标，那么跟踪前后参数λ取不同值时的检测概率Pd如图3所示（跟踪前检测概率恒定，50次蒙特卡洛仿真，6个目标结果取平均值），检测性能得到提高。

图3 跟踪前后检测性能变化曲线

图4给出目标起始时刻不同时的关联跟踪结果，验证了本算法新目标初始化的有效性。

图4 新目标初始化关联跟踪结果

对于交叉目标，考虑方位上较远目标和相近目标交叉两种情况，如图5所示。

图5 交叉目标关联跟踪结果

改进的MHT算法对交叉目标进行跟踪时，虽没有交叉后两条路径分配给同一个目标，但交叉交换现象依然存在，表1给出不同检测概率和虚警个数时的交叉交换次数（表中前一个数字表示较远目标的交叉交换次数，后一个数字表示相近目标的交叉交换次数）。从表中可以看出，检测概率越高、虚警个数越少，完成交叉过程越短，出现交叉交换的可能性越低。

表1 出现交叉交换的次数（50次蒙特卡洛仿真）

4 总结

在检测概率小于1和存在虚警或杂波情况下的目标跟踪，其主要难点在于数据关联。理想情况下，MHT算法是数据关联问题的最优解，但计算量大。本文结合VDA和MHT，提出了一种改进的MHT算法，它通过对假设生成和假设删除过程进行优化，分步进行已知目标的关联跟踪和新目标的初始化，降低计算复杂度，实现快速目标关联跟踪，并且提高了检测性能。对于交叉目标，采用曲线拟合方式预测当前时刻的测量值，降低交叉交换出现的可能。通过仿真分析，验证了该方法的有效性。

[1] RONG LI X, ZHI XIAORONG. A refined strongest neighbor filter for tracking in clutter[C]. Proceedings of the 35thconference on Decision and control, Kobe, 1996:2557-2562.

[2] RONG LI X, BAR-SHAALOM Y. Tracking in clutter with nearest neighbor filters: analysis and performance[J]. IEEE transactions on aerospace and electronic systems, 1996, 32(3):995-1010.

[3] BAR-SHALOM Y, KIRUBARAJAN T, LIN X.Probabilistic data association techniques for target tracking with applications to sonar,radar and EO sensors[J]. IEEE A&E systems magazine, 2005, 20(8): 37-56.

[4] BAR-SHALOM Y, BLAIR W D. Multitarget-multisensor tracking: applications and advances Volume III[M]. Norwood,MA: Artech House, 2002: 175-184.

[5] WILLETT PETER, LUGINBUHL TOD, EVANGELOS GIANNOPOULOS. MHT tracking for crossing targets[C]. SPIE conference on Signal and Data Processing of Small Targets, 2007:66991C:1-12.

[6] WILLETT PETER, RUAN YANHUA, STREIT ROY.PMHT: problems and some solutions[J]. IEEE transactions on aerospace and electronic systems, 2002, 38(3): 738-754.

[7] PULFORD G W. Multi-target viterbi data association,information fusion[C]. The 9th International Conference of ICIF, 2006.