基于改进Chan－ Vese模型的图像分割

杨名宇

（中国科学院 长春光学精密机械与物理研究所，中国科学院航空光学成像与测量重点实验室，吉林 长春 130033）

1 引 言

自Kass等人提出主动轮廓模型［1］以来，基于曲线演化的形变模型已被广泛地应用于图像分割、跟踪等领域。其中，在医学图像分割领域的成功应用［2－6］，使得该模型备受关注。该模型的优点在于将图像分割问题转化为求解泛函的极小值问题，并能有效地融合利用图像自身的低层视觉属性与对待分割物体已有的先验知识，因此可较好地获得分割区域的完整表示，在一定程度上克服了传统非模型分割方法由于自身的局限性使得分割区域的边界可能不完整，以及缺乏结合先验知识能力等缺陷。Malladi、Caselles等人后又提出几何主动轮廓模型［7－8］，该模型基于曲线演化理论和水平集方法，通过水平集函数的零水平集间接的表达物体轮廓，该方式虽不如参数主动轮廓［7］模型直观，但易于处理曲线的拓扑形变。

2001年Chan和Vese提出了基于水平集的Chan－Vese模型，该模型一旦初始化后便可自动检测待分割物体的内部轮廓，并且曲线的初始化与位置、梯度无关，因此该模型既可在很大程度上减少噪声的干扰，又适用于待分割物体边缘模糊甚至不连续的情况。但上述模型在实际应用中都有共同的缺点，即没有明确的算法终止条件。目前常用的做法是预先设定一个迭代次数，但这种做法有其缺点：如果迭代次数设置过小，则不能得到图像的完整分割；反之如果迭代次数设置过大的话，则不能正确地反映出算法性能，造成计算资源的浪费。因此如何设置一个恰当的停止条件对于此类基于能量泛函最小值的分割显得至关重要。

本文提出了一种改进的Chan－Vese模型，并给出了该模型相应算法的终止条件。实验表明改进后的模型在新的算法终止条件下，分割结果正确，并且可以大幅减少原始Chan－Vese模型的迭代次数，且速度更快。

2 曲线演化理论与水平集方法

曲线演化是解决静止或运动图像中分割和目标检测问题的一种有效方法［8－9］。该方法利用闭合曲线或曲面形变的特定规律，定义度量闭合曲线或曲面形变的能量函数，最小化此能量函数可使闭合曲线逐渐逼近图像中指定的目标边缘。该方法将图像分割、运动检测转化为求解泛函的极值问题，因而有大量成熟的数学工具可以直接使用，使得该方法在处理纹理、结构复杂的情况下有较好的效果。曲线演化在具体求解中常以偏微分方程的形式来表达，其表达方式可分为显式和隐式两类。显式表达直接通过曲线的各种参数变化来描述曲线的演化过程；隐式表达则通过隐式函数来描述曲线的演化过程。

水平集方法（Level Set Method）最早由Osher和Sethian［9－10］提出，该方法的基本原理是将运动界面作为零水平集嵌入到高一维的水平集函数中，由闭超曲面的演化方程可以得到水平集函数的演化方程，而嵌入的闭超曲面总是其零水平集，所以最终只要确定零水平集即可确定移动界面的演化结果。经过多年的发展，水平集方法已经在图像分割、拓扑优化、闭合界面演化等领域得到广泛的应用［8－10］。

在水平集方法中，二维曲线的演化问题转化为三维空间中水平集函数曲面演化的零水平集求解问题［10］，这里的水平集指的是由水平集函数值相等的点组成的集合。设φ（t）＝φ（x，y，t）表示t时刻的二维闭合曲线，引入水平集函数后，φ（t）被隐式表示为三维空间上一簇具有相同函数值的曲线，如图1所示。

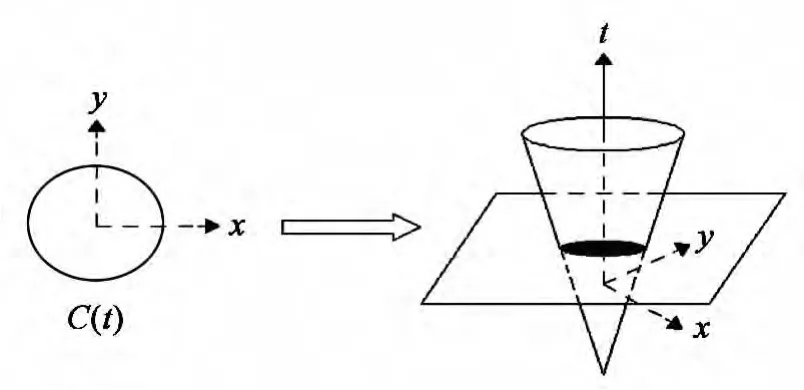
图1 引入水平集后的二维曲线在三维空间表示Fig.1 2Dcurve displayed in 3Dspace with level set

由图1可知，当t＝0时三维曲线C（x，y，t＝0）即为二维曲线c（x，y），此时的封闭曲线为零水平集。不断更新水平集函数即可实现隐含在水平集函数中闭合曲线的演化，而最终水平集函数的零水平集即为曲线的演化结果。因此，水平集方法其实质就是将n维空间的问题映射到n＋1维空间来求解，从而避免了因拓扑结构变化而需做的处理。

在曲线演化过程中，零水平集上的点始终满足

对式（1）两端对t求导得：

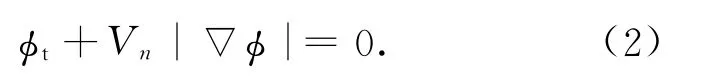
φ为水平集函数，Vn为水平集在法线方向上的速度，曲线的内外区域通常用φ≤0和φ＞0来表示。水平集函数φ通常初始化为符号距离函数，即

其中：设Ω表示图像区域，Ω0为闭合曲线内部区域，∂Ω0为闭合曲线的边界。d（x，y）表示点x和点y的欧氏距离。

3 Chan－Vese模型

Mumford－Shah模型（以下简称 M－S模型）是20世纪80年代提出并被广泛使用研究的一种图像处理模型［11］，该模型通过求解一个广义能量泛函的最小值将图像分割、噪声去除和图像重建三个问题巧妙的融合在一起。Mumford和Shah认为，可以通过最小化下述泛函得到图像的一个分段光滑的近似：

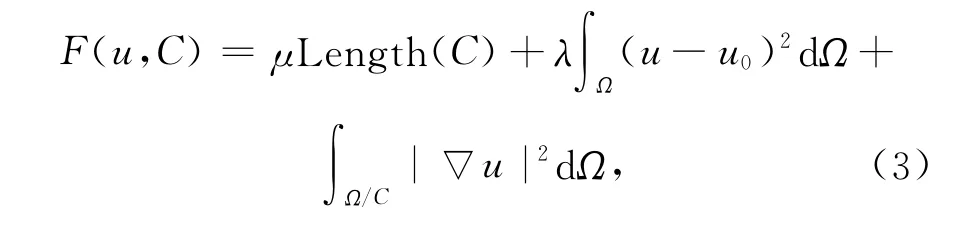
其中：Ω是图像定义域，u0为实际观察到的图像，C是图像u0边缘的连续封闭曲线，u是u0的分段光滑近似。第一项是长度规整项，第二项是能量项，第三项是面积平滑项。

通过求解式（3）的最小值，可以一次性地实现图像的分割、去噪和重建；而且，由于该模型不依赖于图像的梯度信息，因此对具有弱边界、甚至不连续边界的图像也能有较好的分割效果。

但由于M－S模型在具体求解中存在较大难度，因此众多学者分别提出了简化的M－S模型。Chan和Vese提出将原图像分成两个分段光滑的区域，并用每个区域的均值来表示该区域［12］，同时省略了M－S模型中的面积项，模型如下：

结合水平集方法，设Ф是根据初始轮廓线C构造的水平集函数，即｛C｜Φ（x，y）＝0｝，式（4）可写成：

式（5）关于Φ的梯度下降方程为：

由于Chan－Vese模型采用了非紧支且光滑的Hε来近似H，故式（6）与下式具有相同的静态解：

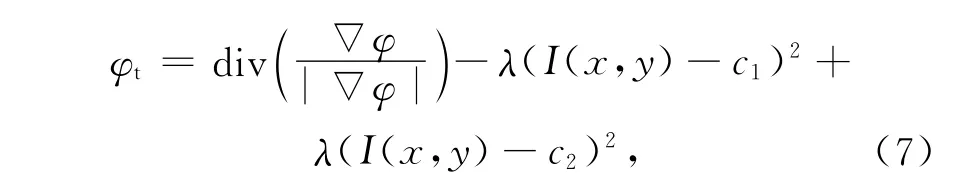
而式（7）又是式（8）对应的梯度下降方程：

由于式（8）是关于Φ的一次齐次函数，一般来说不存在最小值，即随着演化的持续，水平集函数Φ将趋于＋∞或－∞。因此，Chan和Vese提出了将水平集函数Φ约束在［0，1］以求取式（6）的最小值［13－14］的方法。

4 改进的Chan－Vese模型

与上述出发点不同，新模型不是对Φ的取值范围加以约束，而是通过对原Chan－Vese模型进行改动，从而得到算法的终止条件。从Chan－Vese模型式（5）中可以看出，由于Heaviside函数的特性，只有当水平集函数Φ改变符号时，才会对最小化有影响。因此，当演化曲线附着在物体的外层轮廓时，水平集函数Φ在下一步没有改变符号，此时算法就会终止。因此，本文提出如下改进的Chan－Vese模型：

通过在原Chan－Vese模型中加入（ε＋φ）与（ε－φ），可以明确地反映出在每一次迭代中能量项的变化，同时，还可以加快模型的收敛速度；其中ε为一小正数，作用在于控制Φ的大小。Hε（α＋Φ）和Hε（α－Φ）为 Heaviside函数的一个变形，即在原始Chan－Vese模型的Hε（Φ）和Hε（－Φ）分别加上正常数α。由于Heaviside函数的二值性，所以加入正常数α可以使Hε（α＋Φ）中的Φ当Φ＞－α时，随着曲线的演化逐渐趋近于－α；同理，可以使Hε（α－Φ）中的Φ当Φ＜α时，随着曲线的演化逐渐趋近于α。故改进后的能量项将水平集函数Φ的取值范围约束在［－α，α］，随着曲线的演化，Φ将趋向于－α或α，即｜Φ｜将趋近于α。这样，算法的终止条件（Stop Criterion）可以通过下式来确定：

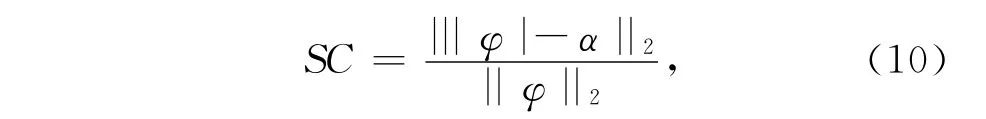
其中：｜·｜2表示2范数，此处定义矩阵设时间步长为Δt，可得如下迭代方程：

A＝（αij）的2范数为

对于式（9）的求解，首先固定Φ，可得c1，c2如下：

再由梯度下降法可得关于φ的偏微分方程，形式如下：

其中：Hε为正则化的 Heaviside函数，δε为正则化的Dirac函数，即Heaviside函数之导数，表示分别如下：

使用有限差分的隐式策略求解式（14），（15）。

5 实验结果对比

下面的实验对比Chan－Vese算法和本文方法对同一幅图像的分割效果。实验环境：CPU为Intel T5500，内存1G，软件平台为 Matlab 7.0，操作系统为 Windwos XP SP3。在以下实验中，λ1和λ2均取作0.5，ε取作0.01，α取作3。

图2 Chan－Vese模型与本文模型分割结果对比Fig.2 Comparison between Chan－Vese model and proposed model

图2是对一幅合成图像的分割实验，其中图2（a）是原始图像及初始轮廓。这里，初始轮廓Φ取作以图像中心为分界，左边为－1，右边为1，图像尺寸为200×200；图2（b）为Chan－Vese模型的分割结果，迭代次数为84次；图2（c）为新模型的分割的效果。由图中可以看出，该图像两种方法的分割效果类似，但新模型在其停止条件下，仅用了18次迭代便自动停止。

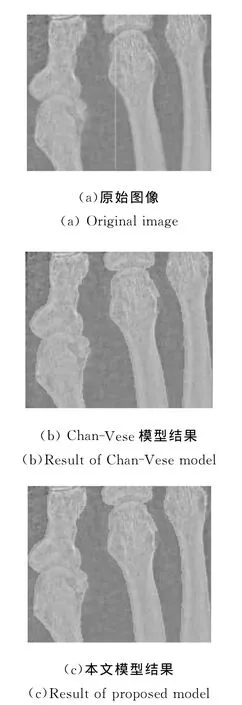
图3 Chan－Vese模型与本文模型分割结果对比Fig.3 Comparison between Chan－Vese model and proposed model

图3是一幅人体脚骨的图像，其中图3（a）是原始图像及初始轮廓。这里，初始轮廓Φ简单的取作以图像中心为分界，左边为－1，右边为1，图像尺寸为150×125；图3（b）为Chan－Vese模型的分割结果，迭代次数为184次；图3（c）为新模型分割的效果。可以看出，Chan－Vese模型在局部出现了一些错误，相比之下，新模型的分割结果更为准确，且在新的停止条件下，仅用了24次迭代便自动停止。表1给出了Chan－Vese模型与本文方法的迭代次数与运行时间对比，可以看出，对于图2和图3来说，新模型的收敛速度比Chan－Vese模型快3～6倍。

表1 Chan－Vese方法与新方法迭代次数和运行时间对比Tab.1 Comparison of iteration number and running timebetween Chan－Vese method and proposed method

6 结 论

针对基于水平集方法的图像分割没有统一、明确的算法终止条件，本文提出一种改进的Chan－Vese模型，并在此基础上明确给出了相应算法的终止条件。在新的算法终止条件下，无需手工设定迭代次数，扩大了算法的实用性。实验结果表明，新模型在新的终止条件下，分割结果正确，与传统Chan－Vese模型相比，新模型的手链速度比Chan－Vese模型快3～6倍，并且具有较好鲁棒性。进一步的研究将集中在水平集函数初始化方面。

［1］ Kass M，Witkin A，Terzopoulos D.Snakes：Active contour models［J］.International Journal of Computer Vision，1988，1（4）：321－332.

［2］ 王醒策，张美霞，武仲科，等.基于全局LBF水平集模型的脑血管层次粗分割［J］.光学 精密工程，2013，21（12）：3283－3297.Wang X C，Zhang M X，Wu Z K.Level coarse brain vessel segmentation based on global LBF model［J］.Opt.Precision Eng.，2013，21（12）：3283－3297.（in Chinese）

［3］ 王卫星，苏培垠.基于颜色、梯度矢量流活动轮廓及支持向量机实现白细胞的提取和分类［J］.光学 精密工程，2012，20（12）：2781－2790.Wang W X，Su P Y.Blood cell image segmentation on color and GVF snake for Leukocyte classification on SVM［J］.Opt.Precision Eng.，2012，20（12）：2781－2790.（in Chinese）

［4］ Chunming L，Chiu－Yen K，Gore C，et al.Minimization of region－scalable fitting energy for image segmentation［J］.IEEE Trans.Image Processing，2008，17（10）：1940－1949.

［5］ 田丰，夏雪，王鹤.真三维显示在医学教育与仿真中的应用［J］.液晶与显示，2012，27（4）：535－538.Tian F，Xia X，Wang H.Applications of volumetric three－dimensional display in medical simulation and education［J］.Chinese Journal of Liquid Crystals and Displays，2012，27（4）：535－538.（in Chinese）

［6］ 张麟，汪源源，王威琪，等.活动轮廓模型和Contourlet多分辨率分析分割血管内超声图像［J］.光学 精密工程，2008，16（11）：2303－2311.Zhang L，Wang Y Y，Wang W Q，et al.Intravascular ultrasound image segmentation based on active contour model and contourlet multiresolution analysis［J］.Opt.Precision Eng.，2008，16（11）：2303－2311.（in Chinese）

［7］ Malladi R，Sethian J A，Vernuri B C.Shape modeling with front propagation：A level set approach ［J］.IEEE Trans.Pattern Analysis and Machine Intelligence，1995，17（2）：158－175.

［8］ Caselles V，Kimmel R，Sapiro G.Geodeisic active contours［J］.International Journal of Computer Vision，1997，22（1）：61－79.

［9］ Sethian J A.Level Set Methods and Fast Marching Methods：Evolving Interfaces in Computational Geometry，Fluid Mechanics，Computer Vision，and Materials Science ［M］.London：Cambridge University Press，1999.

［10］ Osher S，Sethian J A.Fronts propagating with curvature dependent speed：algorithms based on Hamilton－Jacobi formulation［J］.Journal of Computer Physics，1988，79（1）：12－49.

［11］ Mumford D，Shah J.Optimal approximation by piecewise smooth functions and associated variational problems［J］.Comm.Pure Appl.Math.，1989，42（5）：577－685.

［12］ Chan F，Vese L.Active contours without edges［J］.IEEE Trans.Image Processing，2001，10（2）：266－177.

［13］ Chan F，Esedoglu S，Nikolova M.Algorithms for finding global minimizers of image segmentation and denoising models［J］.SIAM J.Appl.Math.，2006，66（5）：1632－1648.

［14］ Bresson X，Esedoglu S，Vandergheynst P，et al.Global minimizer of the active contour／snake model［J］.J.Math.Image Vis.，2007，28（1）：151－167.