基于CS测量矩阵优化的图像融合

孙永明，吴 谨，刘 劲

（武汉科技大学 信息科学与工程学院，湖北 武汉 430081）

1 引 言

图像融合是将多个传感器获得的某一场景的多幅图像进行综合，以获得信息更丰富、更符合人眼视觉特性或更适于计算机处理的新图像。其应用已遍及机场导航、安全监控、医学成像与诊断、机器视觉、智能交通、工业过程及军事等领域。当前大多数图像融合研究工作主要集中在像素级，像素级图像融合存在中间环节数据量大、存储空间大、实时性差等缺点。基于压缩感知（Compressed Sensing，CS）的图像融合技术由于其只对少量的采样数据进行分析处理，解决了中间环节数据量大的问题。

目前国内外对基于压缩感知的图像融合中的采样模式、测量矩阵设计、重构算法以及融合规则问题进行了探索研究。文献［1］比较了3种压缩采样模式对压缩感知重建性能的影响，并进行了图像融合仿真实验，在采样率为50%时仍有较好的融合结果。文献［2］提出了一种基于双放射状采样模式的压缩感知图像融合算法，在相同采样率下比单放射状采样模式的融合效果要好。文献［3］提出了一种基于特征值分解减小Gram矩阵的整体互相关系数的测量矩阵优化方法，在优化速度和重建效果方面都有一定的优势。由于高斯随机测量矩阵硬件实现起来比较困难。因此，设计一种易于硬件实现的测量矩阵是基于CS图像融合的重要问题。

测量矩阵主要有高斯随机矩阵、循环矩阵和哈达玛矩阵。其中高斯随机矩阵最为常用，但由于其不确定性使得硬件实现比较困难；循环矩阵利于存储和硬件实现，但是效果较差，需要对其进行优化；哈达玛矩阵效果最好且易于硬件实现，但N 必需满足N＝2k，k＝1，2，3…，限制了其应用范围。针对以上问题，本文设计了一种由－1，0和1构成的测量矩阵，并对其进行优化，其优点是易于硬件实现，重构效果较好且不受图像大小限制。

2 压缩感知基本原理

压缩感知理论是Candes、Donoho和Tao等人于2004年提出的一种新的信息获取理论，与传统的压缩如文献［4］中所述的压缩有所不同，其核心思想是在信号采样的同时实现信息的压缩，它突破了奈奎斯特2倍最低采样频率的限制。该理论指出，若信号在某个变换域是稀疏的或可压缩的，就可以利用与变换矩阵非相关的测量矩阵将变换系数投影为低维观测向量。这种投影保持了重建信号所需的信息，通过进一步求解稀疏最优化问题就能够从低维观测向量精确地或高概率地重建原始高维信号。因此，将压缩感知理论用于图像融合，在压缩域对少量的线性测量值进行融合，然后对融合的测量值进行重构，这在很大程度上减少了数据量和对存储空间的需求。

假设图像信号X∈RN×N，它的稀疏基为Ψ∈CN×N，ΨΨH＝ΨHΨ＝I，其中I为单位矩阵。利用稀疏基Ψ对X进行稀疏变换，可以得到X在Ψ域的等价表示Θ＝ΨX。

对X稀疏变换后，需要设计一个合理的测量矩阵Φ∈ZM×N，M＜N，实现对信号X的观测取样，获得观测值Y，其大小为M×N。即：

测量矩阵设计的目的是如何采样得到M个观测值，并保证从少量观测值中有效重构出长度为N的高维度信号X，或其等价表示Ψ域下的稀疏向量值。由于观测集合Y的数量小于原始信号X的维数，因此重构信号X变成了一个求解欠定性方程组的问题，不易求解。但当Φ×Ψ满足有限等距特性（Restricted Isometry Property，RIP）［5－6］时，欠定性方程组的求解问题可转化为l0范数的最优化求解问题：

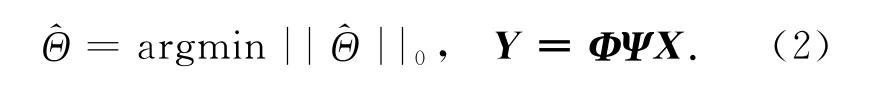
RIP给出了上式高概率重构的条件。因此，Φ×Ψ必须满足RIP条件。而Φ×Ψ是否满足RIP条件由Φ和Ψ间的相关性决定，如果不相关，则Φ×Ψ 具有RIP性质的概率很高［7］。CS理论的框架如图1所示。

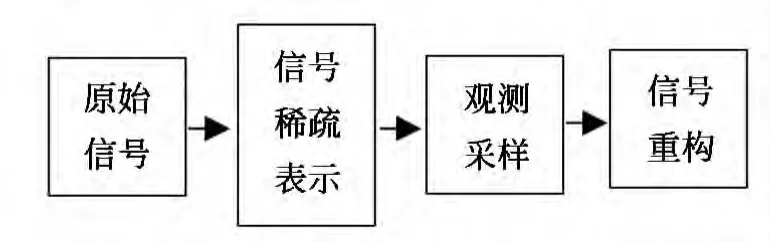
图1 CS理论框架Fig.1 CS theoretical framework

3 测量矩阵设计与优化方法

设D＝ΦΨ，其中Φ为测量矩阵，Ψ为稀疏变换矩阵。设D～表示对D进行列单位化之后的矩阵，则称G＝D～TD～为 Gram 矩阵［8］。为了达到较好的重构效果，测量矩阵Φ和稀疏变换矩阵Ψ的相关性必须要小，即使得D＝ΦΨ有很小的列相关系数，即Gram矩阵的非对角线元素尽可能为零。互相关系数μ可以定义为Gram矩阵所有非对角线元素的绝对值之和，即

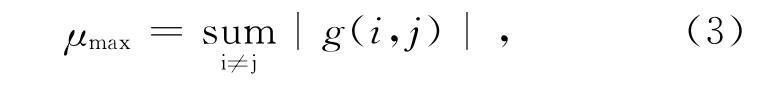
其中：g（i，j）是 Gram 矩阵的元素。

本文对测量矩阵的优化采用模拟退火法，该方法减小互相关系数的核心思想是：按一定的规则改变测量矩阵的每一个元素值，求得改变后相应的互相关系数；如果互相关系数变小，则以一定的概率p（本文中p＝0.5）改变该元素值；否则，保持不变。

Φ生成算法具体步骤如下：

步骤1：生成一个只含有－1、0和1的向量a，长度为N；

步骤2：对向量a以步长1循环移位N次得到向量序列a1，a2…aN得到初始测量矩阵Φ＝［a1，a2…aN］T，大小为 N×N；

步骤3：根据式（3）计算 Gram 矩阵G＝D～TD～的相关系数μ0；

步骤4：依次将0变为1求得相应Gram矩阵的相关系数μ1，将0变为－1求得相应Gram矩阵新的相关系数μ－1；令μnew＝min（μ1，μ－1），如果μnew大于μ0，保持0值不变；否则，如果μ1小于μ－1，将0变为1，如果μ1大于μ－1，将0变为－1。

4 基于压缩感知的图像融合

基于压缩感知图像融合的核心思想是在压缩域对少量的测量值进行融合，然后对融合得到的测量值进行重构，以达到减小中间计算量的目的。

本文基于压缩感知的图像融合方案：

（1）对两幅源图像f1和f2分别进行小波变换，得到小波系数F1和F2；

（2）分别对其小波系数F1和F2进行测量取值，得到测量值Z1和Z2；

（3）按照系数绝对值取大法进行融合，得到融合后的测量值Z；

（4）采用正交匹配追踪 （Orthogonal Matching Pursuit）算 法［9］重构出融合后的小波系数F；

（5）进行小波逆变换，得到融合后的图像f。其框图如图2所示。

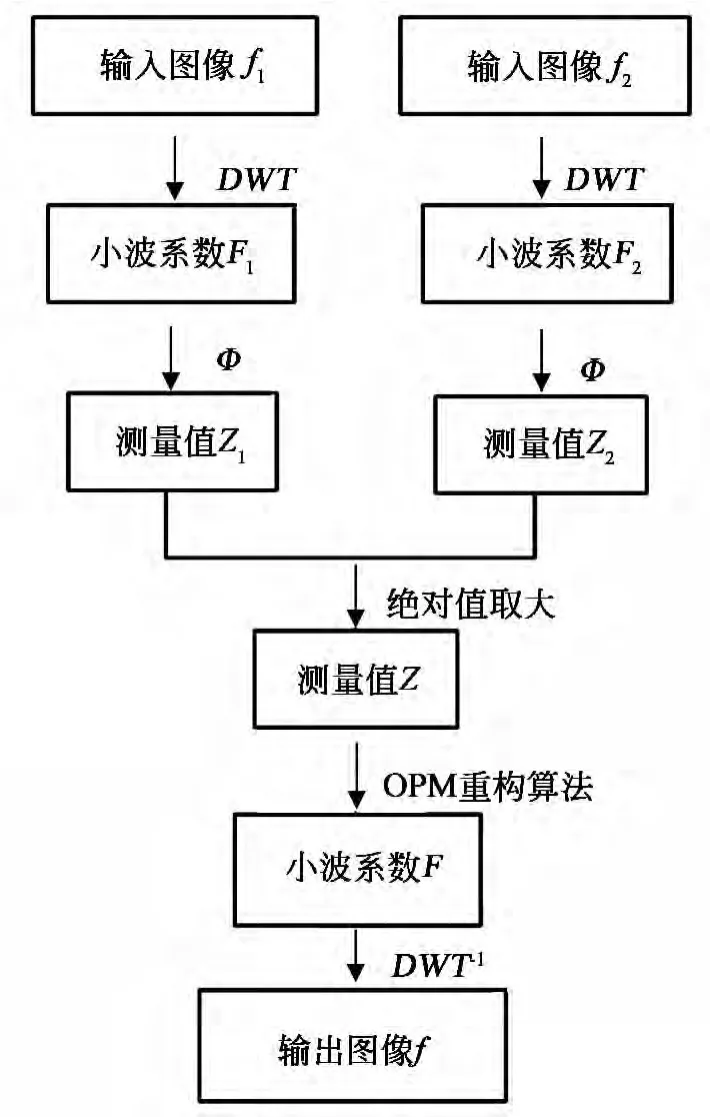
图2 基于CS图像融合框图Fig.2 Image fusion framework based on CS theory

5 实验仿真

5.1 测量矩阵设计及优化实验

选取标准Lena图像（256×256），由3中所提出的方法构造出大小为190×256的测量矩阵，测量矩阵优化前后的重构图像峰值信噪比（PSNR）如图3所示。

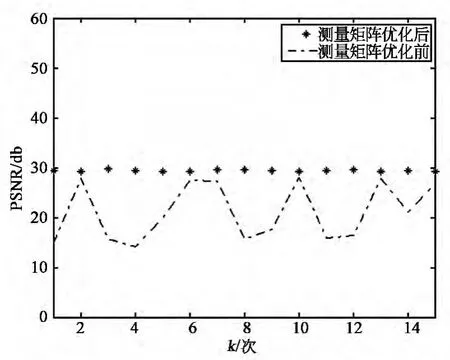
图3 优化前后PSNR值Fig.3 PSNR values before and after optimization

优化前后重构图像PSNR的均值μ和方差σ如表1所示。重构图像的平均PSNR较优化前提高了8.232 5dB。方差近似为零表明优化后的该测量矩阵能保证图像具有较稳定的重构结果。

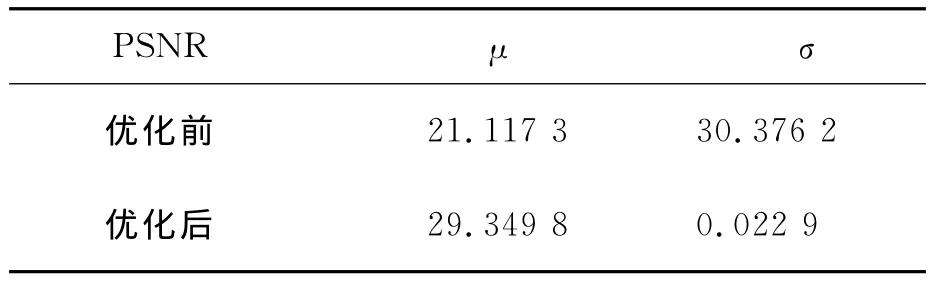
表1 优化前后PSNR的均值和方差Tab.1 Mean value and variance of PSNR before and after optimization

5.2 图像融合实验

实验选取大小为512×512的Clock和Pepsi左右聚焦图像，采样率为50%的情况下，分别用高斯测量矩阵和本文测量矩阵进行CS图像融合，得到融合图像的峰值信噪比（PSNR）、空间频率（SF）、平均梯度（G）［10］如表2和表3所示，融合效果如图4和图5所示。从实验结果数据和融合效果图都可以可以看出，本文测量矩阵基本能够达到高斯测量矩阵的性能，取得了较好的融合效果。

图4 Clock图像融合结果Fig.4 Fusion results of Clock image

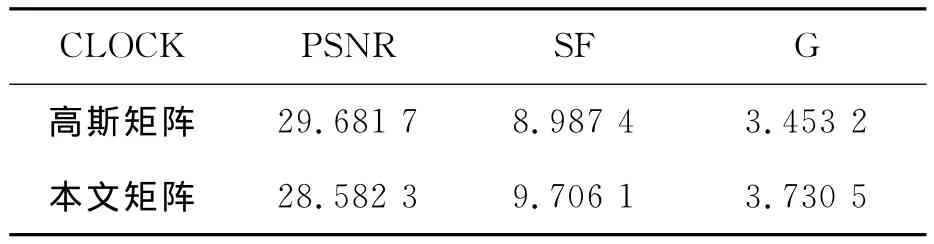
表2 Clock图像融合评价指标Tab.2 Evaluation index of Clock image fusion

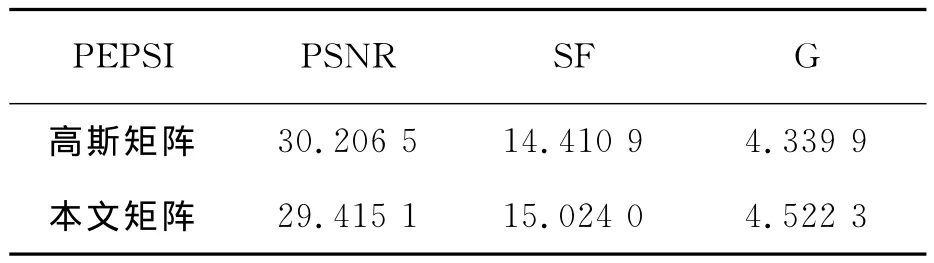
表3 Pepsi图像融合评价指标Tab.3 Evaluation index of Pepsi image fusion

图5 Pepsi图像融合结果Fig.5 Fusion results of Pepsi image

6 结 论

针对随机测量矩阵的不确定性和硬件实现难度大的问题，本文设计的测量矩阵仅含有－1、0和1三个值，其优点是易于硬件实现。实验结果表明，经过优化后的该测量矩阵取得了不错的重构效果。将该测量矩阵用于基于压缩感知的图像融合，在采样率仅为50%的情况下仍能取得较好的融合效果。

［1］ Wan T，Canagarajah N，Achim A.Compressive image fusion ［C］／／Processing of the International Conference on Image Processing，California，USA：IEEE Press，2008：1308－1311.

［2］ 黄晓生，戴秋芳，曹义亲一种基于小波稀疏基的压缩感知图像融合算法［J］.计算机应用研究，2012，29（9）：2581－2583.Huang X S，Dai Q F，Cao Y Q.Compressive sensing image fusion algorithm based on wavelet sparse basis ［J］.Application Research of Computers，2012，29（9）：2581－2583.（in Chinese）

［3］ 赵瑞珍，秦周，胡绍海.一种基于特征值分解的测量矩阵优化方法［J］.信号处理，2012，28（5）：653－657.Zhao R Z，Qin Z，Hu S H.An optimization method for measurement matrix based on eigenvalue decomposition［J］.Signal Processing，2012，28（5）：653－657.（in Chinese）

［4］ 殷亚男，王晓东，李丙玉.基于预测和JPEG2000的MODIS红外辐射多光谱图像无损压缩算法［J］.液晶与显示，2013，28（6）：922－926.Yin Y N，Wang X D，Li B Y.Lossless compression method based on prediction and JPEG2000for MODIS emissive IR bands multispectral image［J］.Chinese Journal of Liquid Crystals and Displays，2013，28（6）：922－926.（in Chinese）

［5］ Donoho D.Compressed sensing［J］.IEEE Transactions on Information Theory，2006，52（4）：1289－1306.

［6］ Candes E，Tao T.Robust uncertainty principles：exact signal reconstruction from highly incomplete information［J］.IEEE Transactions on Information Theory，2006，52（2）：489－509.

［7］ 郑万泽，何劲，魏星，等.基于Contourlet变换的图像压缩感知重构［J］.计算机工程，2012，38（12）：194－196.Zheng W Z，He J，Wei X，et al.Image compressive sensing reconstruction based on contourlet transform ［J］.Computer Engineering，2012，38（12）：194－196.（in Chinese）

［8］ Abolghasemi V，Ferdowsi S，Sanei S.A gradient－based alternating minimization approach for optimization of the measurement matrix in compressive sensing［J］.Signal Processing，2012（92）：999－1009.

［9］ Needell D，Vershynin R.Uniform uncertainty principle and signal recovery via regularized orthogonal matching pursuit［J］.Foundations of Computational Mathematics，2007，9（3）：317－334.

［10］ 傅瑶，孙雪晨，薛旭成，等.基于非下采样轮廓波变换的全彩色图像与多光谱图像融合方法研究［J］.液晶与显示，2013，28（3）：429－433.Fu Y，Sun X C，Xue X C，et al.Panchromatic and multispectral image fusion method based on nonsubsampled contourlet transform ［J］.Chinese Journal of Liquid Crystals and Displays，2013，28（3）：429－433.（in Chinese）