振动压路机模型仿真探讨

2014-05-09张晓曦

交通科技 2014年1期

张晓曦

（江苏省交通科学研究院股份有限公司南京 210017）

在工程质量和进度要求越来越严格的今天，振动压路机一直受到广大施工单位的青睐。随着控制技术和振动压实技术的日益提高，特别是微电子技术、计算机技术和自动化控制计算的不断发展，振动压路机还有不可限量的发展前景。为了更清楚地了解振动过程中加速度的改变对被压材料压实效果的影响，笔者结合试验段实际工程，通过设置压路机的初始参数，对振动压路机进行模拟仿真［1］。

1 基于Matlab／Si mulink对振动压路机控制系

统仿真

Si mulink是Matlab软件的一个工具箱，它是结合了框图界面和交互仿真能力的非线性动态性系统仿真工具，以Matlab的核心数学、图形和语言为基础。Si mulink Blockset是专门为特定领域设计的Si mulink功能块的集合［2－3］。利用它对振动压路机控制系统进行仿真具有重要意义。

（1）在仿真过程中，可以求解各种复杂的代数方程、偏微分方程及积分方程等。在某种程度上，仿真与理论和试验相比，其对问题的认识更为细致、深刻，可以清晰地了解问题本质，而且可重复地、随时地、连续动态地观察事物的发展状况。

（2）可以清晰、直观地解释一些现象，易于分析理解，可以显示发生在结构内部的物理现象。

（3）仿真完善了试验，可以对试验方案的正确制定、试验中的合理测点布置、仪表量程选择等提供更加可信的理论依据。

（4）和试验不同，仿真软件可以复制拷贝，重复利用，可以进行适当改变，以满足不同试验条件的需求

。

2 模型仿真

2.1 理论分析

选择典型机械轮胎驱动振动压路机为对象，写出并分析振动系统运动方程，以两自由度的数学模型为例，见图1。首先假设对模型的有关参数和条件。

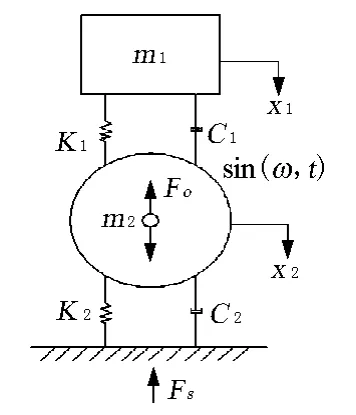
图1 振动压路机数学模型

（1）土是弹性体，具有一定刚度，其值为K2，阻尼为线性阻尼，其值为C2。

（2）振动压路机上车质量为m1，瞬时位移为x1，下车质量为m2，瞬时位移为x2，且上下车简化具有一定质量的集中质量块。

（3）振动碾压过程中，任意时刻振动轮始终保持与碾压面紧密接触。数学模型的运动方程为

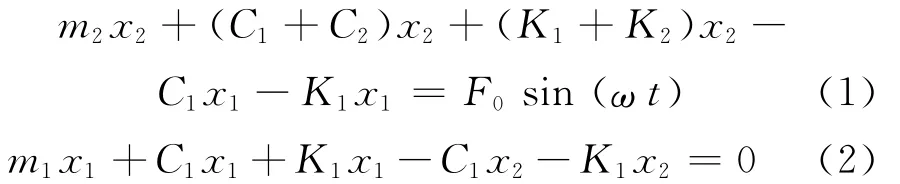
式中：m1为上车的质量；m2为下车质量（振动质量）；K1为减振器刚度；K2为土的刚度；C1为减振器阻尼；C2为土的阻尼；F0为激振力幅值；x1为上车瞬时位移（瞬时振幅）；x2为下车瞬时位移（瞬时振幅）；ω为工作频率（角频率）；Fs为下车对路面的作用力。

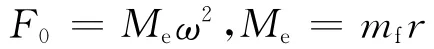
式中：Me为偏心块静偏心力矩；mf为偏心力；r为偏心距。

振动系统与激振力系统有相同的频率ω做强迫振动。式（1），（2）微分方程的解为：

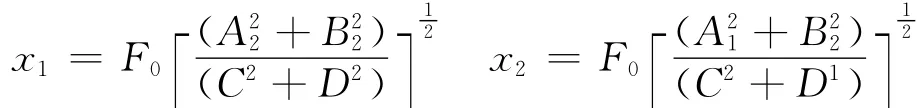
式中：A1＝k1－m1ω2·B1＝C1ω；A2＝k1·B1＝C1ω；C＝m2m1ω4－m2K1ω2－C1C2ω2＋K1K2－m1K1ω2；D ＝ K2C1ω ＋ K1C2ω2－ m2C1ω3－m1C2ω3－m1C1ω3

振动轮在简谐力激振力作用下，垂直加速度幅值为

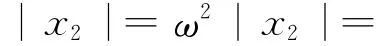
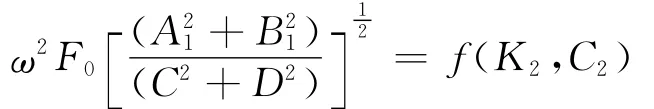
2.2 仿真模型与方法

首先，在Si mulink Library Browser各模块库中选取合适的模块；其次，根据动力学方程所描述的关系构建起系统的仿真框图，见图2。最后在各模块参数修改框中输入初值，保存、运行，进行仿真［4－5］，见图3、图4。

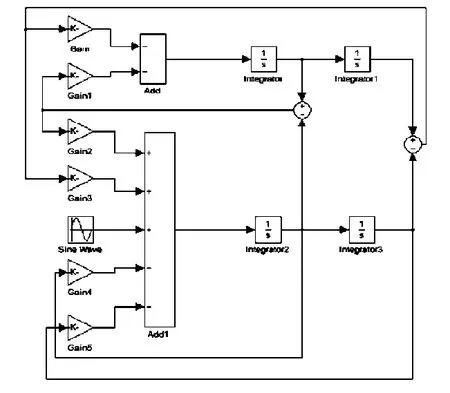
图2 系统仿真图

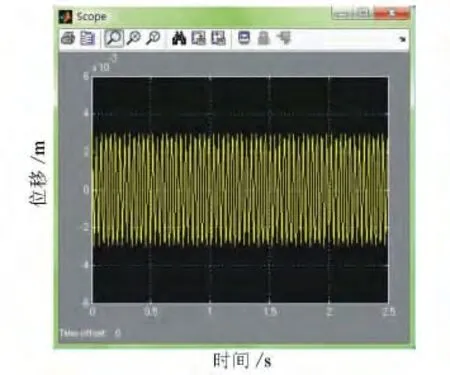
图3 振动轮位移响应

图4 振动轮加速度响应

由图3可见，起振瞬间有较大的位移，此后振动频率增大且趋于稳定，其原因是路堤填石料受迫振动逐渐密实。由图4可见，振动轮是由多同频率的简谐运动叠加而成，而不是一种频率的简谐运动。振动压路机工作时，由于路面的情况复杂多变，其固有频率也不尽相同，这样单一频率激振就显得不足。多频率叠加的复杂激振，使得填石料更方便处于高频状态，对填石料的压实效果更好。

2.3 仿真结果分析

依据工程实际和相关参考文献，仿真时基本参数确定为m1＝3 000 kg，m2＝7 000 kg，F0＝4.3×105N，ω＝2πf，f＝30 Hz，K1＝1.6×106N／m，K2＝1.7×107N／m，C1＝5.25×104Ns／m，C2＝7.0×104Ns／m，ω＝2 300 r／min。

从理论分析了解到，振动加速度的变化与填石料的阻尼、刚度系数等因素有关。为使得仿真更真实，就要考虑这些因素的改变对仿真结果的影响。

当其他参数保持不变，填石料刚度系数由K2变为2 K2时，仿真时域图变化见图5。

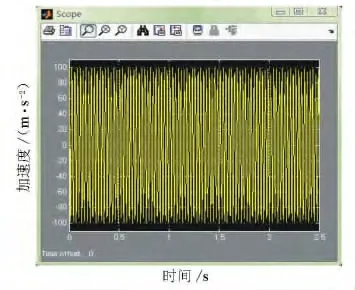
图5 2 K 2情况下振动轮加速度响应

结合图4和图5可见，当填石料刚度为2 K2时，振动加速度的变化率增大，同时加速度幅值也增大，得到的振动轮的垂直加速度与填石料的刚度正相关。仅刚度变化时引起的仿真结果见图6。

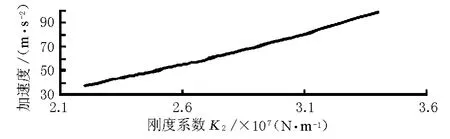
图6 振动加速度随刚度K 2的变化

由图6可见，随着刚度系数的增大，振动加速度也在增大。这表明随着压实度的增大，填石料刚度增大，振动加速度也增大，两者正相关。

当其他参数保持不变，填石料的阻尼由C2变为2C2时，仿真时域图变化见图7。

结合图3和图7可见，阻尼为2C2时，振动加速度的变化频率增大，幅值变小，表明加速度与压实度也是相关的。这一结论与理论分析结果一致。仅阻尼变化时引起的仿真结果见图8。

由图8可见，随着阻尼的增大，振动加速度随之减小，两者负相关。

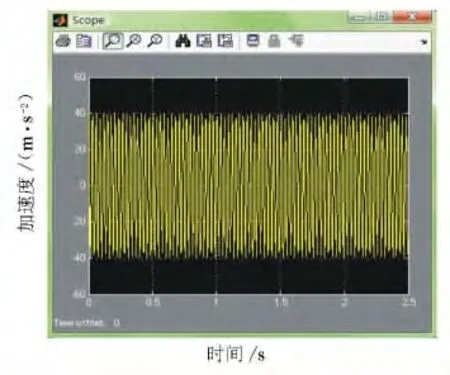
图7 2C2情况下振动轮加速度响应

图8 振动加速度随阴尼C 2的变化

由以上系统模型仿真可以得到：振动压路机的垂直加速度与填石料的阻尼、刚度密切相关。振动轮垂直加速度与路面材料相互作用，使被压填石料的压实密度增大。所以，选取压路机振动轮的加速度间接反映被压路面的压实状况是可行的。

3 信号的采集与分析

在压实过程中，要对压实状态进行动态实时监控，以便了解压实效果的状态变化，这一变化就是一种信息。信息本身不能进行传输和交换，只能通过信号途径才可实现这种传递和交换，信号是通过测试获得的，其最终目的就是获取信息。测试、信号、信息之间的关系见图9。

图9 信息与信号及测试的关系

由于振动压路机对路堤的作用，其状态会随时发生变化，这种变化又可以反馈给压路机，压路机对该反馈作用的信息（动态响应）就是需要获得的信息。该信息是通过测量系统进行采集、存储，最后再传递给分析系统进行合理的分析判断，并发出针对这种反馈信息的指令，目的是为了对压路机及路基进行合理的控制提供可靠的依据，见图10。

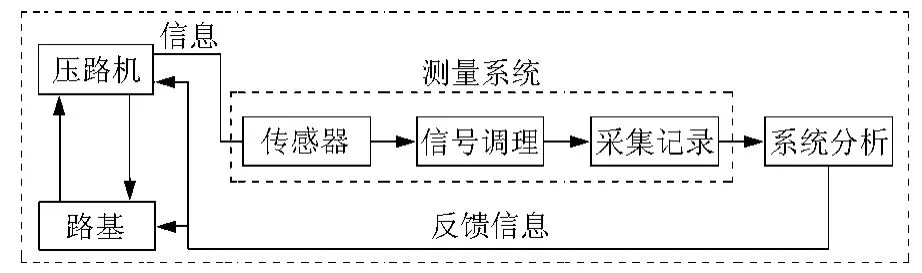
图10 压实过程信息的传递与获取

经过振动信号分析、信号处理（信号滤波、噪声分析、信号变换算法），最终反映信号。通过Matlab编程，对采集并经过处理的振动加速度信号进行Fourier变换，结果见图11。图11中出现了振动加速度幅值基波频率和多次谐波频率。图中50 Hz对应的幅值为主频对应的幅值，120 Hz对应的幅值为二次谐波对应的幅值。通过分析比较，取出基波和二次谐波成份，将其比值（CMV）作为路堤连续压实质量控制的指标。

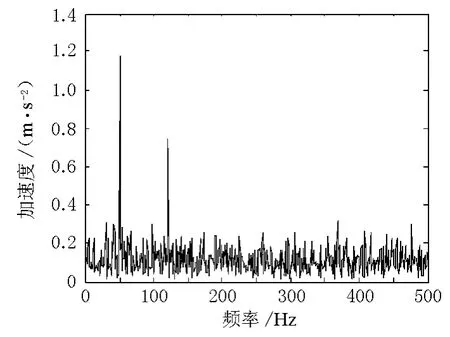
图11 振动加速度信号频谱

4 现场试验

根据仿真试验理论，选取某项目进行现场试验。本试验段为某单线电气化I级干线标准铁路，设计时速为120 k m／h。填石料最大粒径10 c m，不均匀系数10～30，粗颗粒含量大于70%，摊铺厚度45 c m的填石料，在自重19.8 t，强振时振动力43 t、弱振时振动力26 t、刚度3.1×107N／m、阻尼2.2×105Ns／m作用下，在相同条件下可以达到较好的压实效果；CMV取值62.2可以作为参考值。