差分模型和灰色理论组合预测模型在桥梁施工控制中的应用
2014-05-09朱伟伟杨逸江
朱伟伟 杨逸江
(长江生态(湖北)科技发展有限责任公司 武汉 430014)
随着桥梁跨度的不断增大,我国规定必须对大跨度桥梁进行施工控制,以保证桥梁施工的安全性。连续梁桥是目前应用较多的一种结构形式,主要采用悬臂现浇对称施工。而施工中受多种不确定因素的影响,增加了桥梁监控工作的难度。虽然通过现场数据的实时采集、设计参数误差的识别与修正、精确计算模型的不断重建,大部分不确定影响因素可以被消除,但这种方法使得数据采集和模拟计算的工作量大大增加,加上计算模型与实际结构也存在差别,有些状况甚至无法模拟,因此有必要寻找一种更简单、更有效的控制方法。
本研究以内蒙古包头镫口黄河特大桥施工监控为背景,利用最优加权组合预测模型的基本原理,提出了差分模型和灰色系统理论中的新陈代谢GM(1,1)模型的组合预测模型,预测梁段的应力值,为桥梁施工控制中的实时预测提供了一种新的途径。
1 最优加权组合预测模型
设预测对象的一个观测序列X=(x1,x2,…,xn),对x采用k种不同的预测方法,预测结果^X=,…)。式中:=(x1,j,x2,j,…xn,j)表示第j种预测方法所得的预测序列。设k种预测方法在组合预测模型中的权重W=(w1,w2,…wk),则组合预测模型为[1-2]
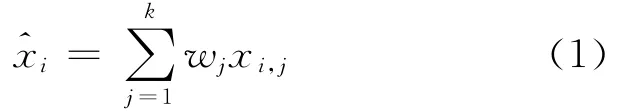
式(1)模型的预测误差ei为

由式(1)和式(2)得
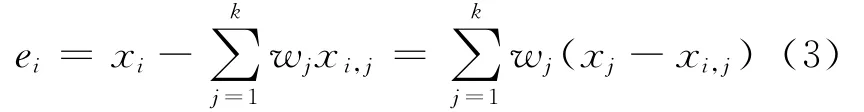
令ei,j=xi-xi,j,由式(3)得

组合预测模型的关键之一是估计预测模型式(1)中的权重wj,本文采用最小二乘法准则(误差平方和最小),从而转化为求解下述优化模型
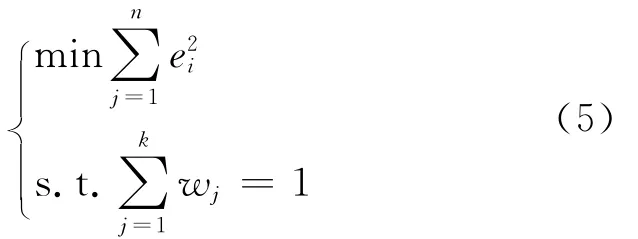
令
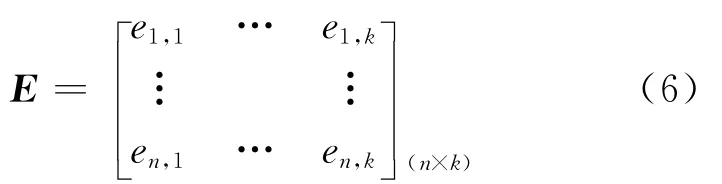
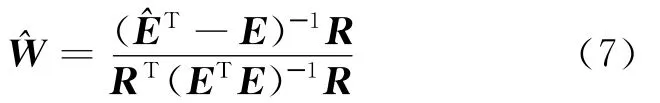
式中:R=(1,1,…,1)T(k×1)。
2 差分模型和灰色系统理论中的新陈代谢GM(1,1)模型
2.1 差分模型[3]
设上述观测序列X=(x1,x2,…xn),其一阶差分序列定义为

式中:Δxi=xi+1-xi。
应用差分模型预测时,若采用一阶差分模型,则在i时刻预见期为 Δt的预测值^xi+Δt为
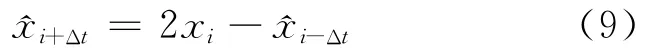
式(9)称为一阶差分预测模型。依此类推,可得其他差分预测模型。实际应用时,首先要根据观测序列确定预测模型的阶数。
2.2 灰色系统理论中的新陈代谢GM(1,1)模型
灰色系统理论就是以灰关联空间为基础的分析体系,它以现有信息或原始数列为基础,通过灰过程及灰生成对原始数列进行数据加工与处理,建立灰色预测模型方程。通常灰色模型表示为GM(m,n),即m阶n个变量的灰色微分方程模型,当时就构成了邓聚龙教授提出的灰色预测GM(1,1)模型。当数据序列的新数据补充进去、去掉老数据,并保持其维数不变,这样的模型称作新陈代谢 GM(1,1)模型[4]。
2.2.1 GM(1,1)模型
将上述观测序列 X=(x1,x2,…xn)记为X(0)(k):

利用式x(1)(k)=x(0)(k)对 X(0)(k)作一次累加生成
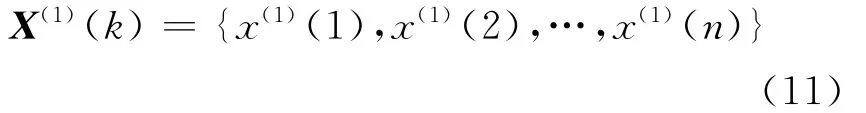
累加生成数据序列X(1)(k)可建立如下白化形式的微分方程
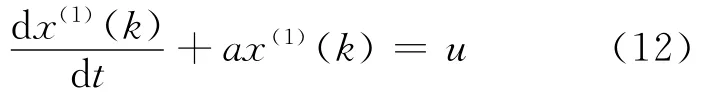
其解为

式中:参数a,u可由下述公式求解
对式(13)作一次累减生成,可得原始数据序列 X(0)(k)的预测函数为
2.2.2 模型精度检验
后验差检验法是一种被普遍采用的GM(1,1)模型精度检验方法。后验差检验是残差统计特性的检验,该方法以各点的预测误差为基础,通过计算后验差比值C和小误差频率P获得模型的精度级别。将实测值作为原始数据(k=1,2,…,n),建立 GM(1,1)模型并获得预测值(k=1,2,…,n),则残差为
记原始序列和残差序列的均值分别为^x(0),¯q(0),计算原始数列和残差数列的方差分别为
计算后验差比值

小误差频率
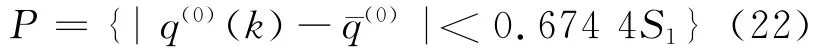
指标C越小越好。C越小,表示S1越大而S2越小,表明尽管原始数据很离散,而模型所得计算值与实际值之差并不太离散。指标P越大越好。P越大,表明残差与残差平均值之差小于给定值0.674 4 S1的点较多[5]。
按C与P 2个指标,可综合评定预测模型的精度。见表1。

表1 模型精度指标
如果检验不合格,可建立残差GM(1,1)模型来修正原模型,待模型合格后再进行预测分析。
3 应用实例
结合内蒙古包头镫口黄河特大桥的施工,建立差分模型和灰色系统理论中的新陈代谢GM(1,1)模型的组合预测模型来预测梁段应力值,并通过预测值与实测值的分析比较,验证了该组合预测模型的预测精度。
内蒙古包头镫口黄河特大桥是是鄂尔多斯市树林召至包头东兴公路跨越黄河大桥,全长6.355 k m,桥面宽12.5 m,行车道宽11.5 m,主桥结构型式为55 m+9×100 m+55 m,上部结构主桥为预应力变截面连续箱梁,采用挂篮对称悬臂施工,逐节段向前推进。引桥为40 m装配式部分预应力混凝土连续箱梁。
现以包头镫口黄河特大桥某一施工节段为例,来说明差分模型和灰色系统理论中的新陈代谢GM(1,1)模型的最优组合预测模型在桥梁施工控制中的应用。应力控制截面位于墩顶0号块附近悬臂梁根部,在浇筑0号块混凝土前,用扎丝将钢弦式应变传感器捆扎在控制截面箱梁上、下缘纵向钢筋上,测点布置见图1。
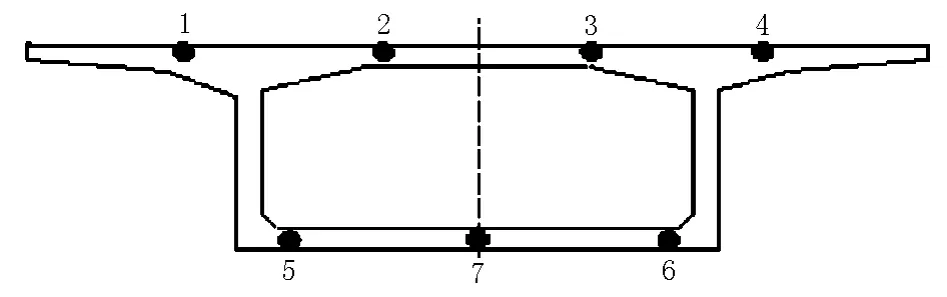
图1 箱梁横截面测点布置示意图
取116号墩悬臂箱梁5号节段已施工完毕并已移出挂篮为该施工状态,建模时以包头侧2,3,4和5号4个节段张拉预应力后根部上缘4个点(见图1)的平均实测应力值作为原始序列来预测6号块预应力张拉后116号墩根部上缘应力值。
单个模型预测分别为
差分模型经模型识别采用一阶差分模型^x5=2x4-x3=7.14,预测值见表2中第(3)栏。与实测值比较,预测值的相对误差为

灰色系统理论中的新陈代谢GM(1,1)模型:原始序列为X(0)(k)={1.94,3.49,4.42,5.78};累加生成序列为 X(1)(k)={19.4,5.43,9.85,15.63};代入式(14)得到灰微分方程的参数列为[a,u]T=[-0.253 5,2.529 4]T;白化方程为-0.253 5x(1)(k)=2.529 4;由式(13)得其解为^x(1)(k+1)=11.92e0.2535k-9.98;又由式(17)得预测序列为 ^X(0)(k+1)={1.94,3.44,4.43,5.71};后验差比值C=0.024 8<0.35;小误差频率P=1>0.95;可见,模型精度很好,为一级,可用于后续应力的预测。当k=4,^x(0)(5)=7.36,则6号块张拉后116号墩根部上缘应力预测值为7.36;与实测值比较相对误差为
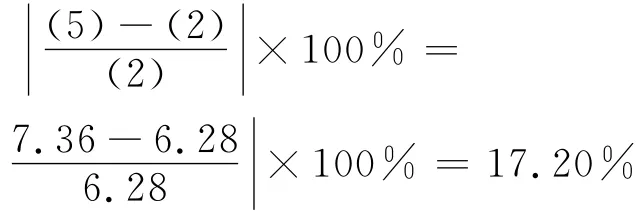
同样,取116号墩悬臂箱梁6号节段已施工完毕并已移出挂篮为该施工状态,建模时以包头侧3,4,5和6号4个节段张拉预应力后根部上缘应力实测数据作为原始序列来预测7号块预应力张拉后116号墩根部上缘应力值。依此类推可得到8号块预应力张拉后116号墩根部上缘应力值。
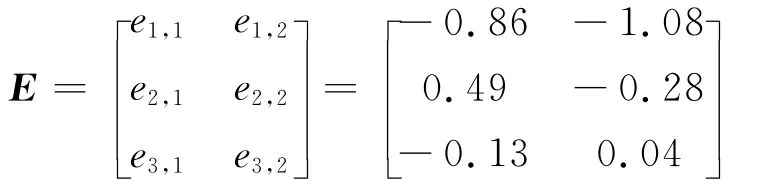
根据最优加权组合预测模型的原理,残差矩阵E为
具体应力实测值与3种模型的预测结果对比见表2。
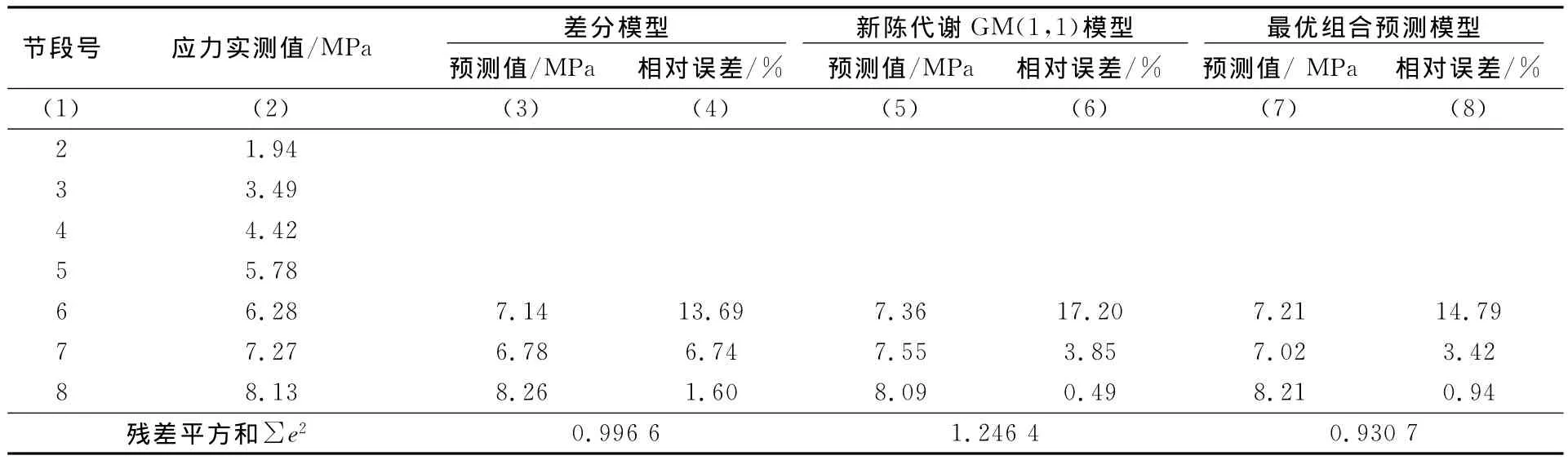
表2 应力实测值与3种模型的预测结果对比
从计算结果来看,最优组合预测模型的相对误差处于差分模型和灰色系统理论的新陈代谢GM(1,1)模型之间,且均小于15%,具有较好的稳定性;残差平方和∑e2比各单个预测模型有所减小,可见差分模型和灰色系统理论中的新陈代谢GM(1,1)模型的最优组合模型在桥梁施工控制中的预测精度较单个预测模型要好。
4 结论
(1)最优组合预测模型的相对误差处于差分模型和灰色系统理论的新陈代谢GM(1,1)模型之间,且均小于15%,具有较好的稳定性;残差平方和∑e2比各单个预测模型有所减小,因此,最优组合预测比各单个预测模型有较高的精度和较好的稳定性,而且运用 Matlab等程序很容易实现计算过程,是一种切实可行的科学建模方法。
(2)最优组合预测的精度取决于个单个预测模型的精度,还与模型的数量和关联程度有关。因此,提高单个预测模型的精度是提高组合预测模型精度的关键。
(3)最优组合预测模型用于桥梁施工控制中,能够预测出精度较高的各节段应力值,具有很好的实时性,能及时控制桥梁施工的未来发展。若能进一步研究桥梁施工控制中的其他各种预测方法的不同最优组合,或许能获得精度更高的桥梁施工控制预测方法。
[1] 赵梅娟,王钟羡.组合预测在应力集中问题中的应用[J].机械强度,2006,28(1):96-098.
[2] 李秀珍,孔纪名,王成华.最优加权组合模型在滑坡变形预测中的应用[J].自然灾害学报,2008,17(2):53-57.
[3] 程银才,李明华,范世香.基于差分模型和最小二乘法的组合预测模型在实时洪水预报中的应用[J].中国农村水利水电,2009(11):50-52.
[4] 熊和金,徐华中.灰色控制[M].北京:国防工业出版社,2005.
[5] 邓聚龙.灰色系统基本方法[M].武汉:华中理工大学出版社,1996.
