基于改进TOPSIS法的城市公交发展水平评价方法

谢晓琳 ，张卫华，丁 恒，王胜萍

随着国民经济的持续增长和城市化进程的不断加快，中国机动车拥有量急剧增加。汽车保有量的迅速增长使得城市交通压力倍增，导致道路容量严重不足，公共交通发展滞后，公交分担率低。交通拥堵、交通安全、停车困难及空气污染等交通问题接踵而至。优先发展城市公共交通已成为解决城市发展进程中交通需求、能源消耗及环境保护等诸多问题的出路。20个世纪80年代，一些交通专家就提出了中国必须优先发展公共交通，这是中国大城市交通发展的必由之路。然而，实际上许多大城市的公共交通事业却是在一片优先之声中并未能真正得到加强。

目前，城市公共交通的不足之处包括：公交设施用地难以保证、资金投入不足、路权优先措施少、服务质量与公交吸引力不高及智能化信息化程度低等方面。由于城市公共交通中种种不足的客观存在，从另一层面反映出城市公交整体发展潜力巨大。各个城市公共交通的发展因其经济和人口等因素的不同而产生差异，通过对城市公共交通的发展水平进行评价分析，有助于挖掘城市公共交通的发展潜力，为城市公共交通的发展规划和管理等方面提供依据，从而提高公共交通的分担率，缓解城市交通拥堵，对整个城市公共交通的发展起到积极的推动作用，具有一定的现实意义。

1 评价指标的建立

1.1 指标体系建立的原则

1）整体完备性原则：从不同侧面反映城市公共交通发展的特征和状况。

2）客观性原则：保证评价指标体系的客观公正，保证数据来源的可靠性、准确性和评估方法的科学性。

3）系统性原则：指标体系应能全面反映城市公共交通合理发展水平的综合情况。

4）可操作性原则：指标体系中的每一个指标都必须是可操作的，指标含义明确，能够及时收集到准确的数据，计算简单，易于掌握。

5）独立性原则：每个指标要内涵清晰、相对独立，同一层次的各个指标之间应尽量不相互重叠，相互间不存在因果关系。指标体系要层次分明，简明扼要。

1.2 评价指标体系的构建

城市公共交通系统是一个非常复杂的系统，其要素包括流动的人、行驶的车和变化的路。其评价指标有很多种，对城市公共交通发展水平的评价应当选择尽量少的指标，反映最主要和最全面的信息。作者拟采用层次分析法，分别从城市公共交通的运营能力、服务能力及发展能力等3个方面选择公共交通发展水平的指标，采用塔式结构建立评价体系［1－2］，如图1所示。

图1 城市公共交通发展水平评价指标体系Fig.1 The evaluation index system of urban public transport development level

2 城市公共交通发展水平评价模型

2.1 评价方法

目前，用于城市公共交通发展水平评价的方法主要有层次分析法、模糊综合评价法、数据包络分析法和人工神经网络以及各种方法的组合［3］。不同的评价方法具有各自的优、缺点和实用性。作者拟采用的是改进的 TOPSIS法［4－5］，将评价指标分成成本型指标、效益型指标和区间型指标，运用极差变换法对指标进行量化［6］，再计算相对贴近度，对城市公共交通的发展水平进行评价。

2.2 结构熵权－改进TOPSIS法的评价模型

基于结构熵权－改进TOPSIS法的城市公共交通发展水平评价模型的主要思想是：首先基于熵理论，使用主观赋值法与客观赋值法相结合的结构熵权法，获得指标体系中评价指标的权重；然后运用改进的TOPSIS法，对城市的公共交通发展水平进行评价。

2.2.1 结构熵权法

结构熵权法是把主观赋值法与客观赋值法相结合，同时又把定量分析与定性分析相结合，用于测评指标体系权重的新方法。其主要思想是：通过分析指标及其相互关系，将采集专家意见的德尔菲专家调查法与模糊分析法相结合，形成“典型排序”，用熵理论对“典型排序”进行熵值计算和“盲度”分析，并对可能产生潜在的偏差数据做统计处理。最后计算出总体认识度，归一化后即得到指标的综合权重［7］。其步骤为：

1）征询专家的意见，形成初始的“典型排序”。

2）对“典型排序”进行“盲度”分析，用熵理论计算数据的熵值，减少初始排序的不确定性。假设有k个专家参加调查，获得的问卷调查表有k张，每一张表对应的指标集为U＝｛u1，u2，…，un｝，指标集的初始排序矩阵记作：A＝A（aij）k×n（i＝1，2，…，k；j＝1，2，…，n），其中：aij为第i位专家对第j个指标uj的评价。对初始排序进行定性和定量转换，定义转换熵函数为：

式中：r为专家依据初始排序的样式对某个指标评价后给出的定性排序数。

令m＝s＋1，s为实际最大顺序号，将排序数r＝aij代入式（3）可得到定量转换值bij（（uaij）＝bij），矩阵B＝（bij）k×n为隶属度矩阵，平均认识度记为bj，bj＝（b1j＋b2j＋…＋bkj）／k，表示k 位专家对指标uj的一致看法。专家zi对因素uj由认识产生的不确定性称为“认识盲度”，记作Qj。

对于每一个因素，定义k位专家关于u的总体认识度为xj，则：

由xj即得k位专家对指标uj的评价向量X＝（x1x2… xn）。

3）归一化处理，得到运用结构熵权算出的权重：

处理后的结果ωj即为每个指标j的综合权重。

2.2.2 改进的TOPSIS法

逼近于理想解的排序方法（technique for order preference by similarity to ideal solution，简称为TOPSIS法）是有限方案多目标决策分析的一种常用方法。该方法的基本思想是：基于归一化后的原始数据矩阵，找出有限方案中的最优方案和最劣方案（分别用最优向量和最劣向量表示），然后分别计算各评价对象与最优方案和最劣方案间的距离，获得各评价对象与最优方案的相对接近程度，以此作为评价优劣的依据。但是，TOPSIS法求规范矩阵时比较复杂，不易求出正理想解和负理想解，而且权重是事先确定的，具有一定的主观性和随意性［8］。因此，本研究采用改进的TOPSIS法对城市公共交通的发展水平进行评价。

改进的TOPSIS评价方法的步骤为：

1）对矩阵进行规范化，得到标准化矩阵Rij＝（rij）m×n。

将城市公共交通发展水平的评价指标变量进行规范化处理，将其转换为［0，1］范围内。对于定量化的指标，根据其属性将其分为成本型、效益型和区间型。定义rij∈［0，1］为样本模式i评价指标xj的指标xij的标准化值，则3种类型指标的标准化转换函数为：

对于成本型指标（其值越小越好），

对于效益型指标（其值越大越好），

对于区间型指标（其值在某一区间［a1，a2］为最佳），

式中：xjmax＝max｛xij｜i＝1，2，…，m｝，xjmin＝min｛xij｜i＝1，2，…，m｝。

对于定性化的评价指标，采用专家评分的方式，进行归一化处理，使其指标介于［0，1］之间。

2）确定绝对正理想解和绝对负理想解。

使用TOPSIS法的关键是要确定合理的绝对正理想解和绝对负理想解。在对原始数据进行标准化处理后，决策数据均转化为［0，1］间的值，故绝对正理想解可设定为向量（1）n×1＝（1 1 …1）T；绝对负理想解可设定为向量（0）n×1＝（0 0… 0）T。

3）计算各个决策方案到绝对正理想解和绝对负理想解的距离：

4）计算相对贴近度：

5）按照相对贴近度的大小对各个城市公共交通发展水平进行排序，数值越大，则说明其发展水平越高。

城市公共交通发展水平评价模型如图2所示，运用该模型评价的主要步骤为：①运用结构熵权法计算权重ωj。②运用改进的TOPSIS法，得到相对贴近度。③根据相对贴近度的大小，得出城市公共交通发展水平的排序。

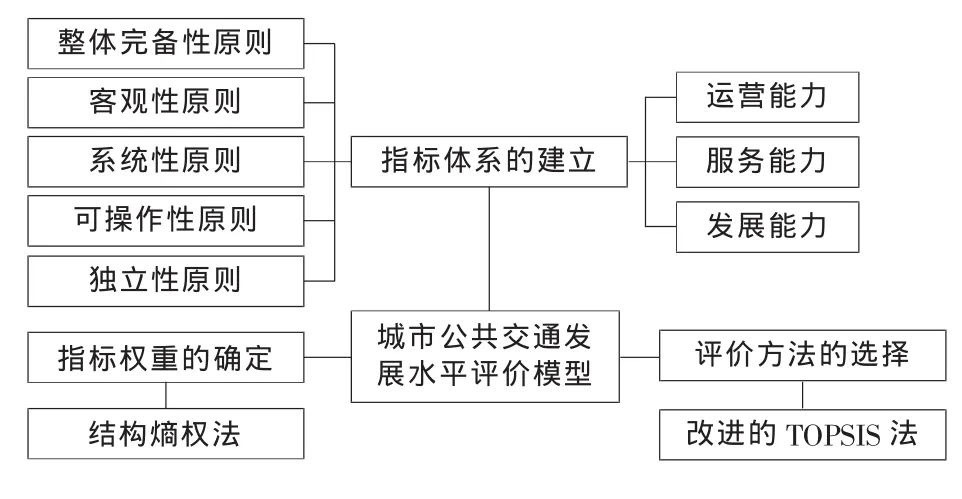
图2 城市公共交通发展水平评价模型Fig.2 The evaluation model of urban public transport development level

3 实例分析

基于A城市和B城市2012年的调查数据，分别从运营能力、服务能力和发展能力对其公共交通发展水平进行比较分析。

1）根据结构熵权法，确定指标权重ωj，见表1。

2）运用改进的TOPSIS法，计算相对贴近度。

通过对A城市与B城市进行调查，所得的各项指标见表2。表2中的规范值／范围为国家相关规范及十二五发展规划中的建议值／范围，万人拥有量的范围则是根据A城市及B城市的人口等相关资料进行预测分析的建议范围。

表1 基于结构熵权法的评价指标权重Table 1 The evaluation index weight based on the structure entropy weight method

运用改进的TOPSIS法，求出的到正、负理想解的距离和相对贴近度见表3。智能化公交建设是定性指标，按照拥有一个智能化公共交通服务中心为1、公交智能服务中心建设已起步为0.8、公交智能服务中心建设刚刚起步为0.6及缺乏公交智能服务中心为0.4进行智能化公共交通指标的标准化。

从表3中可以看出，在公共交通运营能力、服务能力和发展能力的评价中，A城市的相对贴近度均优于B城市的。然后采用加权平均的方法对公共交通发展水平的综合相对贴近度进行计算，A城市的综合相对贴近度为0.552 7，而B城市的综合相对贴近度为0.404 0。由此可知，A城市的公共交通发展水平优于B城市的。对照表2中两个城市公交发展水平各个现状的指标可以看出：A城市的线网密度、线路重复系数、公交车辆进场率、平均发车间隔、平均站距及公交分担率等指标均比B城市的更接近规范值或规范范围，故A城市的公交综合发展水平优于B城市的，这与运用改进的TOPSIS法进行评价的结果相一致，也从另一层面说明了B城市的公共交通较A城市的更具有发展潜力。由此可见，B城市可效仿A城市的公共交通发展，通过减少线路重复系数、提高公交车辆的进场率和车均场站面积、缩短车辆的发车间隔和站点的平均间距等措施来提高其公交的发展水平。

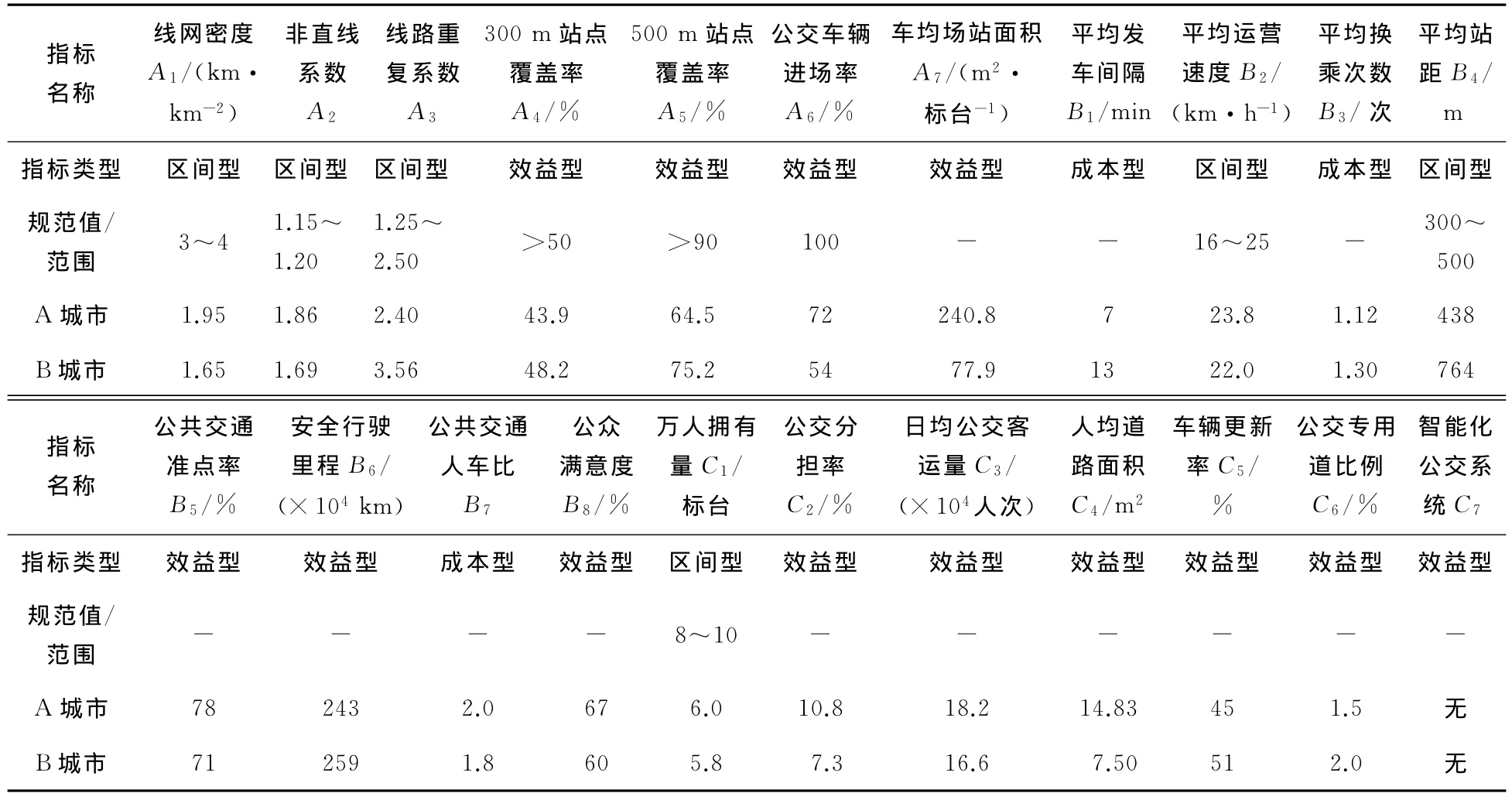
表2 A城市与B城市2012年评价指标及其范围Table 2 The evaluation index value and its scope in 2012of city A and city B

表3 基于改进的TOPSIS法的公交发展水平相对贴近度比较Table 3 The relative closeness degree of the public transport development level based on the improved TOPSIS method

4 结论

根据整体完备性、客观性、系统性、可操作性及独立性等原则，从城市公共交通的运营能力、服务能力和发展能力等3个方面建立指标体系。然后，运用主观与客观相结合的结构熵权法，确定指标权重。运用改进的TOPSIS法，建立评价模型。最后，通过对A城市和B城市两个城市的公共交通发展水平进行比较分析，分别评价了两个城市的运营能力、服务能力和发展能力，并运用综合加权法计算综合发展水平，对两个城市的公共交通综合发展水平进行了分析。分析结果表明：运用改进的TOPSIS法对城市公共交通的发展水平进行评价，具有良好的可操作性和实用性。

（

）：

［1］ 王炜，杨新苗，陈学武.城市公共交通系统规划方法与管理技术［M］.北京：科学出版社，2002.（WANG Wei，YANG Xin－miao，CHEN Xue－wu.Urban public transportation system planning method and management technology［M］.Beijing：Sciences Press，2002.（in Chinese））

［2］ 乔欢，张鹤.城市公共交通发展评价指标体系研究［J］.交通与运 输，2009（12）：62－65.（QIAO Huan，ZHANG He.The development evaluation system of public transport research［J］.Traffic and Transportation，2009（12）：62－65.（in Chinese））

［3］ 李远远，云俊.多属性综合评价指标体系理论综述［J］.武汉理工大学学报：信息与管理工程版，2009，31（4）：305－309.（LI Yuan－yuan，YUN Jun.Synthetic research on the theory of multiple－attributed comprehensive evaluation index system［J］.Journal of Wuhan University of Technology Information ＆ Management Engineering，2009，31（4）：305－309.（in Chinese））

［4］ 乔永辉.一种基于TOPSIS的多属性决策方法研究［J］.企 业 技 术 开 发，2006，25（9）：89－91.（QIAO Yong－hui.A study for the multide－attibuted decisionmaking method based on TOPSIS［J］.Technological Development of Enterprise，2006，25（9）：89－91.（in Chinese））

［5］ 周亚.多属性决策中的 TOPSIS法研究［D］.武汉：武汉理工大学，2009.（ZHOU Ya.The study of the TOPSIS method in multiple attributed decision making［D］.Wuhan：Wuhan University of Tchnology，2009.（in Chinese））

［6］ 李美娟，陈国宏，陈衍泰.综合评价中指标标准化方法研究［J］.中国管理科学，2004，12（10）：45－48.（LI Mei－juan，CHEN Guo－hong，CHEN Yan－tai.Study on the target standardization method of the comprehensive evaluation［J］.Chinese Journal of Management Science，2004，12（10）：45－48.（in Chinese））

［7］ 程启月.评测指标权重的结构熵权法［J］.系统工程理论与实践，2010，30（7）：1225－1228.（CHENG Qiyue.Structure entropy weight method to confirm the weight of evaluating index［J］.Systems Engineering－Theory ＆ Practice，2010，30（7）：1225－1228.（in Chinese））

［8］ 陈伟.关于TOPSIS法应用中的逆序问题及消除的方法［J］.运 筹 与 管 理，2005，14（3）：39－43.（CHEN Wei.The problem and elimination of rank reversal in the application of the TOPSIS method［J］.Operations Research and Management Science，2005，14（3）：39－43.（in Chinese））