基于Rao－Blackwellised粒子滤波的岩石声发射信号去噪

凌同华，刘伟宏，朱 亮，吴联迎

在岩石声发射的信号处理中，信号去噪是最基础、也是最关键的一项工作。目前，信号去噪处理的方法主要有两种：频域和时间－空间域分析方法。假设噪声和期望信号成分在频域范围内相互不重叠，可以通过频域方法滤除噪声（如：高通滤波、带通滤波及带阻滤波等）。例如：白噪声分布于整个频域范围内，传统的频域方法已经不能清除噪声成分。相反，一种基于噪声统计特性的状态空间方法被用来去除噪声成分。在时域上建立起来的常用滤波有：维纳滤波、卡尔曼滤波［1－2］及扩展卡尔曼滤波等。维纳滤波局限于处理线性平稳静态过程，并具有很好的效果。卡尔曼滤波常被用于处理非静态过程的信号。当需要确保滤波精度时，动态系统需满足线性且噪声服从高斯白噪声分布。另外，扩展卡尔曼滤波已被用来处理非线性系统，但对预测状态的估值问题仍需线性化处理，噪声要求服从高斯分布。

近几年，迅速发展起来的粒子滤波［3－5］（Particle Filter，简称为PF）是一种基于蒙特卡罗的非线性、非高斯系统状态估计的滤波方法，完全突破了卡尔曼滤波理论框架，对系统的过程噪音和量测噪音不加任何限制。在PF基础上，作者拟提出Rao－Blackwellised 粒 子 滤 波 （Rao－Blackwellised particle filter，简称为RBPF）来加强岩石声发射信号采集质量。

1 粒子滤波

从动态系统中获取信息和估计系统的状态，建立一个精确的模型是至关重要的。大多数物理现象服从随机分布，其状态可以用有限维向量描述，并通过向量差分方程来模拟。建立PF系统模型，至少需要两个方程：①状态方程，用于描述系统状态随时间演变的过程；②观测方程，用于将系统在某时刻的输出和系统的状态联系起来。

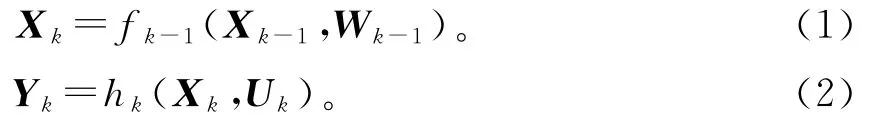
式中：Xk，Yk分别为动态系统在k时刻的状态向量和观测向量；f 为状态函数；h为观测函数；Wk－1，Uk分别为状态过程和观测过程的噪声。

粒子滤波算法流程如图1所示，其详细过程见文献［3，4］。

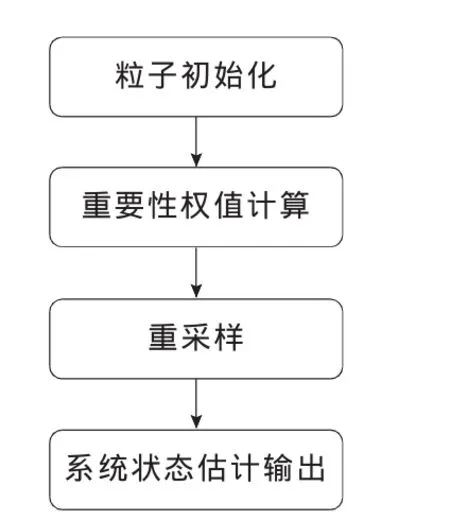
图1 PF算法流程Fig.1 Flow chart of PF algorithm

2 Rao－Blackwellised粒子滤波

2.1 RBPF方法

由于声发射信号的采集频率比较高（通常在兆赫兹以上），粒子滤波需要大量的样本点来组建后验概率分布，使计算效率下降。尤其在高维状态空间和实时监控应用中，计算效率下降较明显。为实现粒子滤波在实时声发射监控中应用，采取具有降维作用的 RBPF［6－9］。

RBPF将标准状态空间向量xk分解成两个子空间，其中一部分x1k可以通过卡尔曼滤波进行分析解计算；而另一部分x2k可通过粒子滤波计算，并使其计算的复杂程度大大降低。RBPF的目的就是用较少的粒子获取同样的估计精度，从而降低计算量，实现其成本的节约与推广应用。基于两个子空间所构成的条件概率，并对其进行推演：

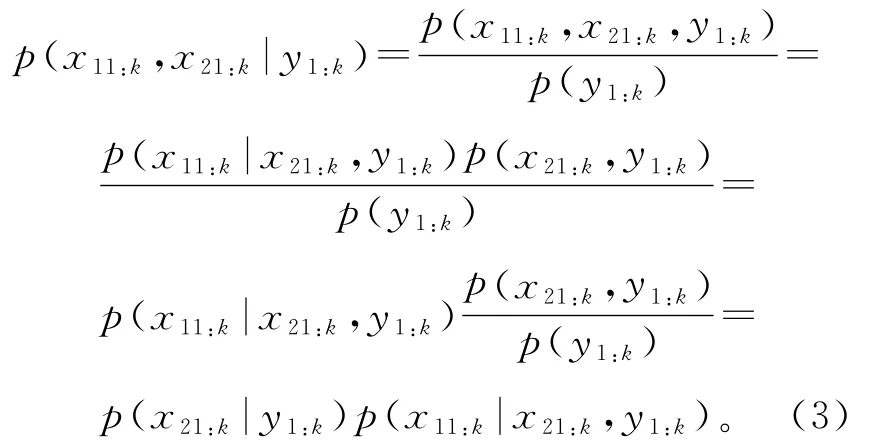
式中：p（x21：k｜y1：k）为x21：k的后验概率密度函数。

如果p（x11：k｜x21：k，y1：k）服从条件线性高斯分布，则可通过卡尔曼滤波实现其最优估计。因此，由两个子空间构成的后验概率密度函数通过运用粒子滤波估计时，仅需考虑与x21：k相关的一部分。RBPF可以看成是卡尔曼滤波与粒子滤波的结合体，是一种加强的粒子滤波。

2.2 RBPF实时处理特征

RBPF是一种状态空间时域的滤波技术，每次输入一个新的数据算法立即更新。在更新过程中，RBPF不依赖于全部已输入的信号序列，仅需考虑前一时刻的数据。因此，在采集过程处理信号时，对采集数据长度和采样频率没有特殊要求，此外，RBPF在计算过程所需存储数据的空间将大大降低，其运算速度获得较大的提高。断铅试验常被用来模拟声发射源，断铅试验中采集的声发射信号如图2所示。从图2中可以看出，滤波效果不受采集数据长度的影响。RBPF进行信号去噪处理时不受将来采集数据的干扰，仅与当前时刻及前一时刻所处的状态有关。传统的滤波器不具有这一特征，在滤波过程中需要完整的数据链。由于RBPF有实时在线处理功能，并能处理高维的非线性非高斯系统，而备受研究者的关注。

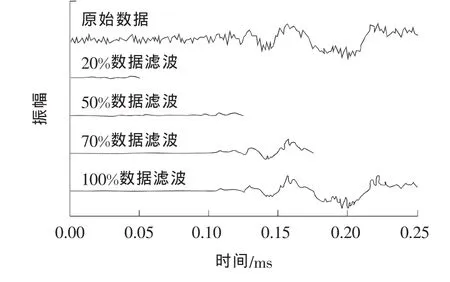
图2 RBPF实时处理信号滤波的特征Fig.2 The real－time processing feature of RBPF based signal filtering

3 RBPF在声发射信号去噪中应用

3.1 状态空间模型的建立

由于地震波信号与声发射信号具有相似性，地震波模型可以成为合适的候选对象来代表结构中的声发射事件。其模型为：

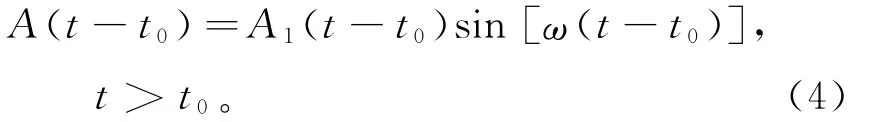
式中：A1（t－t0）为声发射源波形的振幅；t0为波形到达时间；ω为主导角频率（ω＝2πf）。

在处理地震数据中，类似的方法被其他学者采用，地震波的振幅可用随机过程X1（t）表示，同时地震波用随机过程Xw（t）表示，则该过程可以改写为：

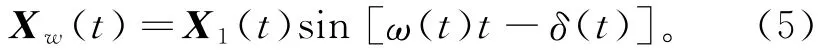
式中：δ（t）为相位角。

由于高斯－马尔卡夫（Gauss－Markov）过程能用来模拟许多物理现象，其中也包括模拟地震波的振幅X1（t），其离散形式为：

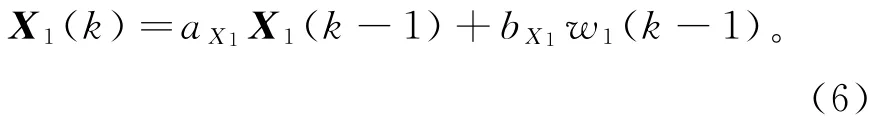
假定状态空间的噪声部分也可用高斯－马尔卡夫过程代替，其表达式为：

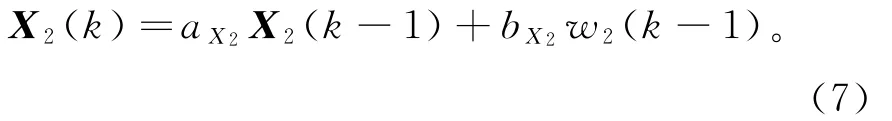
式中：aX2，bX2均为高斯－马尔卡夫过程的参数；w2与w1相互独立。

这些方程中涉及的参数可通过声发射信号的噪声部分确定。

利用模型式（6），（7），声发射的状态空间系统可以构造为：

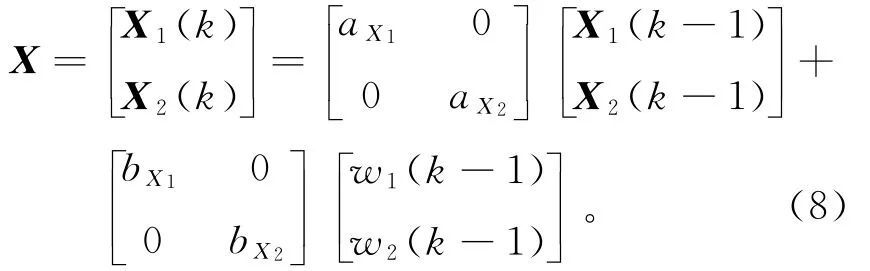
此外，其量测方程构造为：

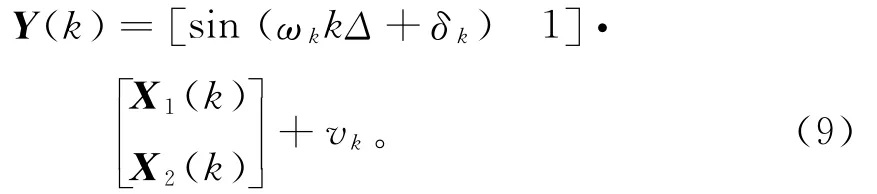
式中：ωk为第k时间步长的主频率；vk为量测噪声。

式（8），（9）可分别用简化的矩阵形式表示为：

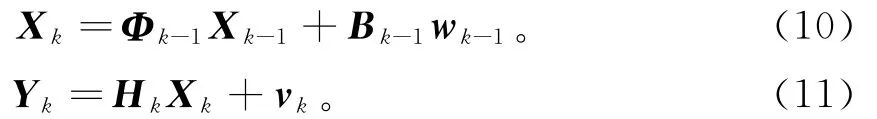
由于没有固定的主导角频率，通过运用频率粒子集［ωik］Mi＝1，会比运用具体指定的频率有更高的估计精度。在研究中，每一个粒子的动态函数和量测函数分别为：

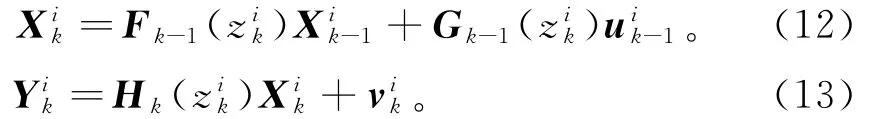
从式（12），（13）可知，每一个粒子的状态和量测函数均为线性。从另一个角度来说，本研究提出了用RBPF的方法来估计声发射信号，即由标准卡尔曼滤波处理状态更新，同时利用粒子滤波处理非线性的量测函数。

3.2 基于声发射信号去噪的RBPF算法

完整RBPF算法的步骤为：

1）卡尔曼滤波初始化：X1（0）＝0，X2（0）＝Y0；误差协方差在实验过程中，发现：R选择相对较大值时，能得到一个较满意的结果；递推过程收敛时，R的选取对滤波结果影响甚小。

2）状态估计预测和误差协方差预测：

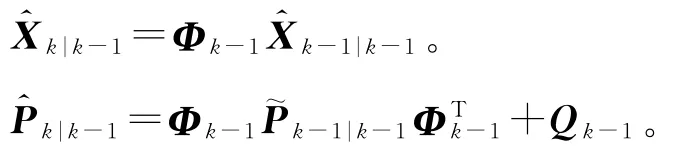
3）粒子更新：

①采样ωik～p（ωk），zik＝sin（ωikkΔ），i＝1，2，…，M；

②计算外推量测估计和方差：

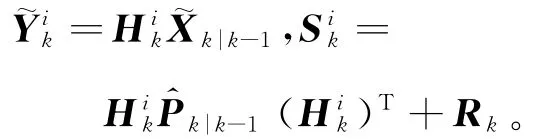
式中：Rk为量测函数中观测噪声的方差，即vk～（0，Rk）。

③计算预测密度：

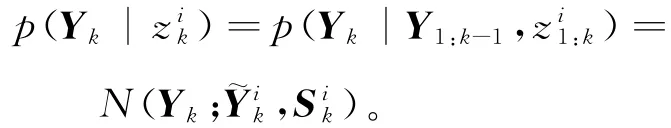
④计算每个粒子的重要性权重：

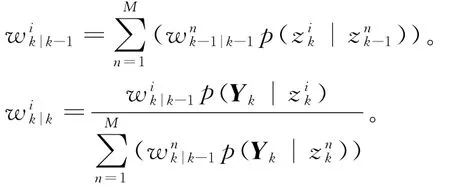
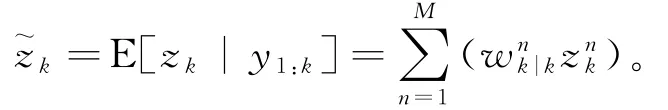
⑥更新量测矩阵：G～k＝［1 z～k］。

8）设定k＝k＋1，回到步骤2）。

针对算法中出现的参数，需要说明：

Φk－1能够根据状态函数的先验知识设定初值，Φk－1可分两种情况考虑：①时变性，即随时间需要更新或传递；②时不变性。在岩石冲击声发射实验中，由于实验环境相对较简单，且RBPF用于声发射信号去噪目前处于探索性阶段，因此仅考虑时不变性，设定，其中：a1，a2均为高斯－马尔卡夫过程中的参数，详细的解释可参考式（6），（7）。a1，a2合适的取值可以从信号的噪声部分（没有目标信号参与进行采集）和附有噪声的信号序列中获取。

Qk－1为状态过程噪声的协方差，其表达式为：

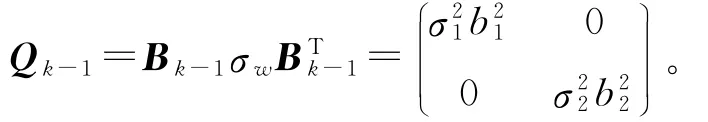
假定噪声的方差为时不变随机过程，那么，Qk－1为固定值Q。Q矩阵可通过信号的噪声部分初始化，确定Q的步骤为：①采集没有目标信号参与的噪声信号，即采集周围噪声；②计算采集噪声信号的自相关性；③利用模型σ2e－β｜τ｜对自相关数据进行拟合，其中：σ，β均通过回归分析确定。

利用该方法可获得σX2和βX2。在探讨过程中，观测噪声的方差假定为相对较小的常数。

3.3 RBPF仿真实验

为检验RBPF的滤波效果，借助于Matlab对其进行仿真模拟。首先需要构造一个不受噪声污染的原始信号作为标准信号，便于与其加噪处理后进行滤波所得结果比较。为验证RBPF处理噪声信号的效果，需对原始信号（如图3（a）所示）加入高斯密度分布的噪声，其附加噪声的方差为0.2，附加噪声的信号如图3（b）所示。对加噪信号运用RBPF进行滤波处理，处理后的信号如图3（c）所示。

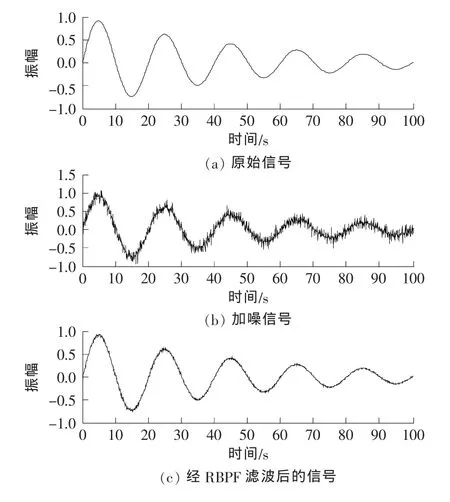
图3 仿真结果Fig.3 Simulation results

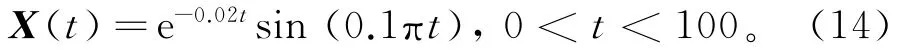
从图3中可以看出，RBPF在信号去噪处理中能获得较好的滤波效果。

3.4 RBPF在声发射信号去噪中应用

试验数据来源：利用SHPB系统对两组石灰岩进行冲击荷载作用下声发射试验，具体试验装置如图4所示。采集两组声发射数据X11和X21，在采集过程中有噪声干扰，利用本研究提出的RBPF处理采集的声发射数据，对应的去噪信号分别为X21和X22，经RBPF后的结果如图5所示。

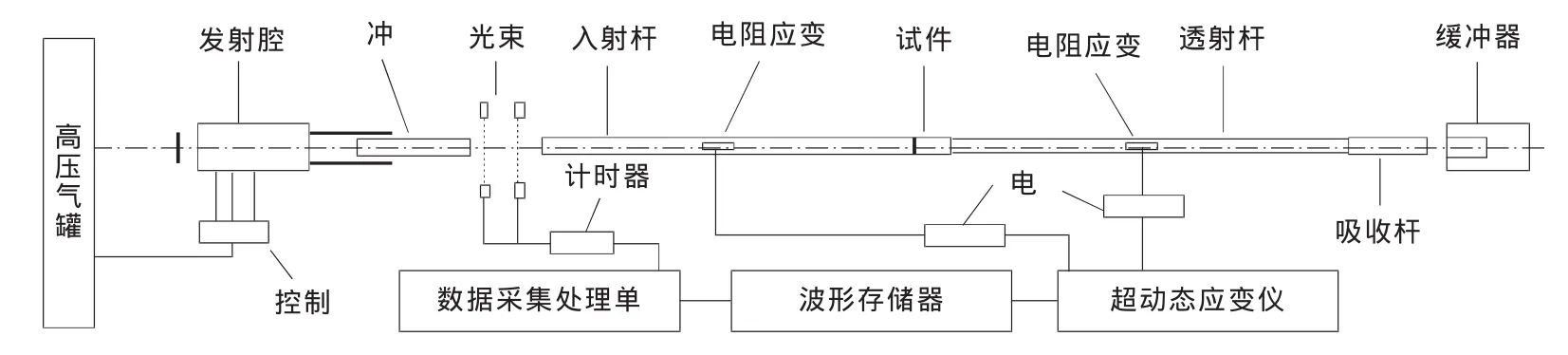
图4 SHPB测试系统Fig.4 SHPB testing systems

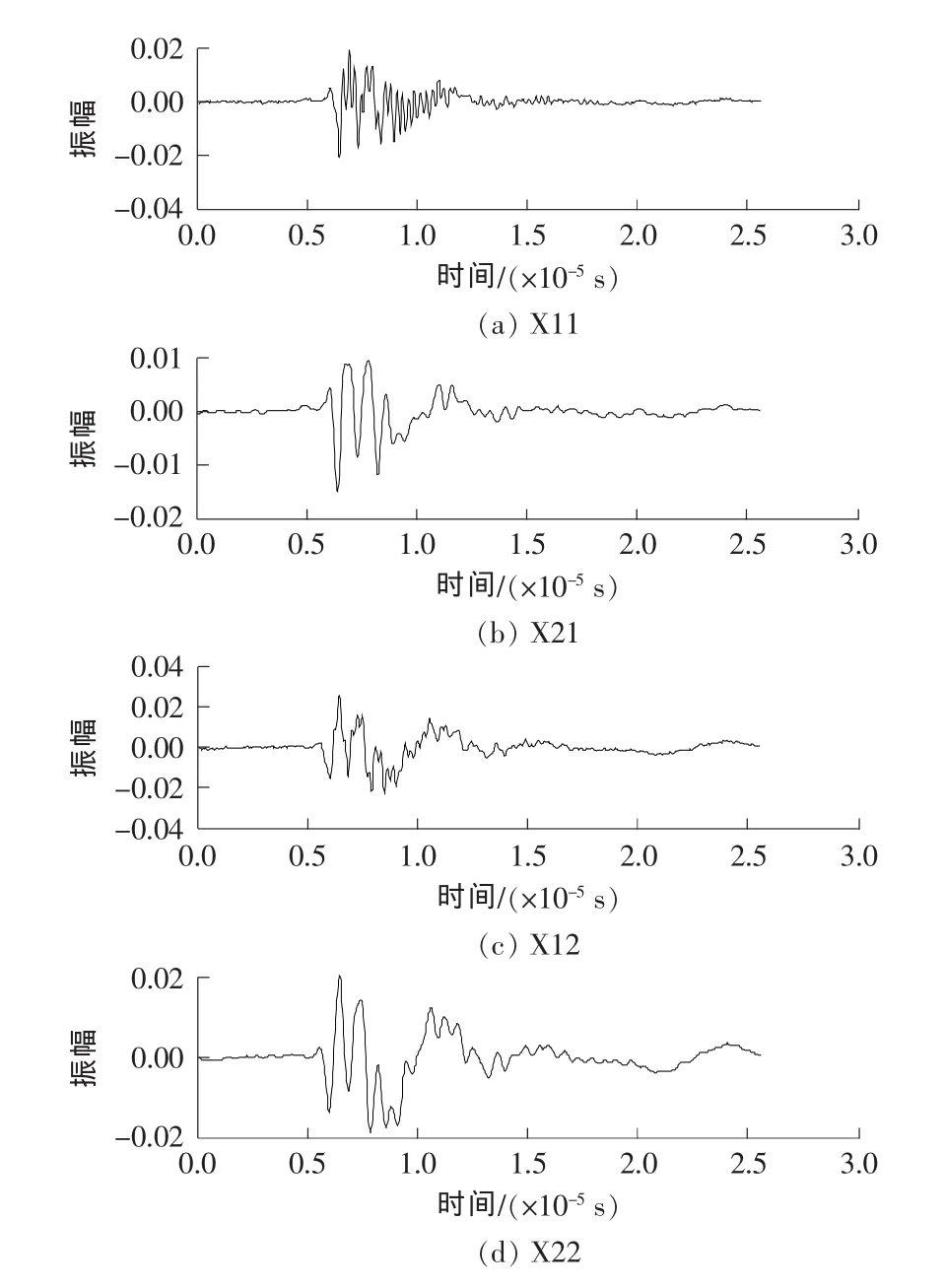
图5 X11和X21为原始信号，X12和X22为其对应的去噪信号Fig.5 X11and X21as original signals，X12and X22as corresponding denoising signals

在处理两组声发射数据时，粒子总数取200，噪声按高斯－马尔卡夫过程模拟，计算时间常数Tc＝4.5×10－4ms，方差σ＝6.7×10－3v2。声发射源的采样频率40MHz，并遵循假设：开始波形的振幅为零，X1（1）＝0；第一个测量值y1设定为噪声，即X2（1）＝y1。

为进一步分析声发射数据并检验RBPF的效果，利用FFT求出图5中各信号的频谱图，如图6所示。从图6中可以看出，X11最大振幅所对应的频率分别为0.15，1和3MHz，而X21最大振幅所对应的频率分别为0.15和1MHz。X21在0.15和1MHz对应的幅值分别高于X11所对应的点，而在3MHz时，两者相差不大，甚至低于X11的，在3MHz出现的现象由噪声所致。通过RBPF对原始信号进行去噪，发现两者在3MHz的幅值都趋于零。可见，RBPF在处理声发射信号中具有很大的潜力。

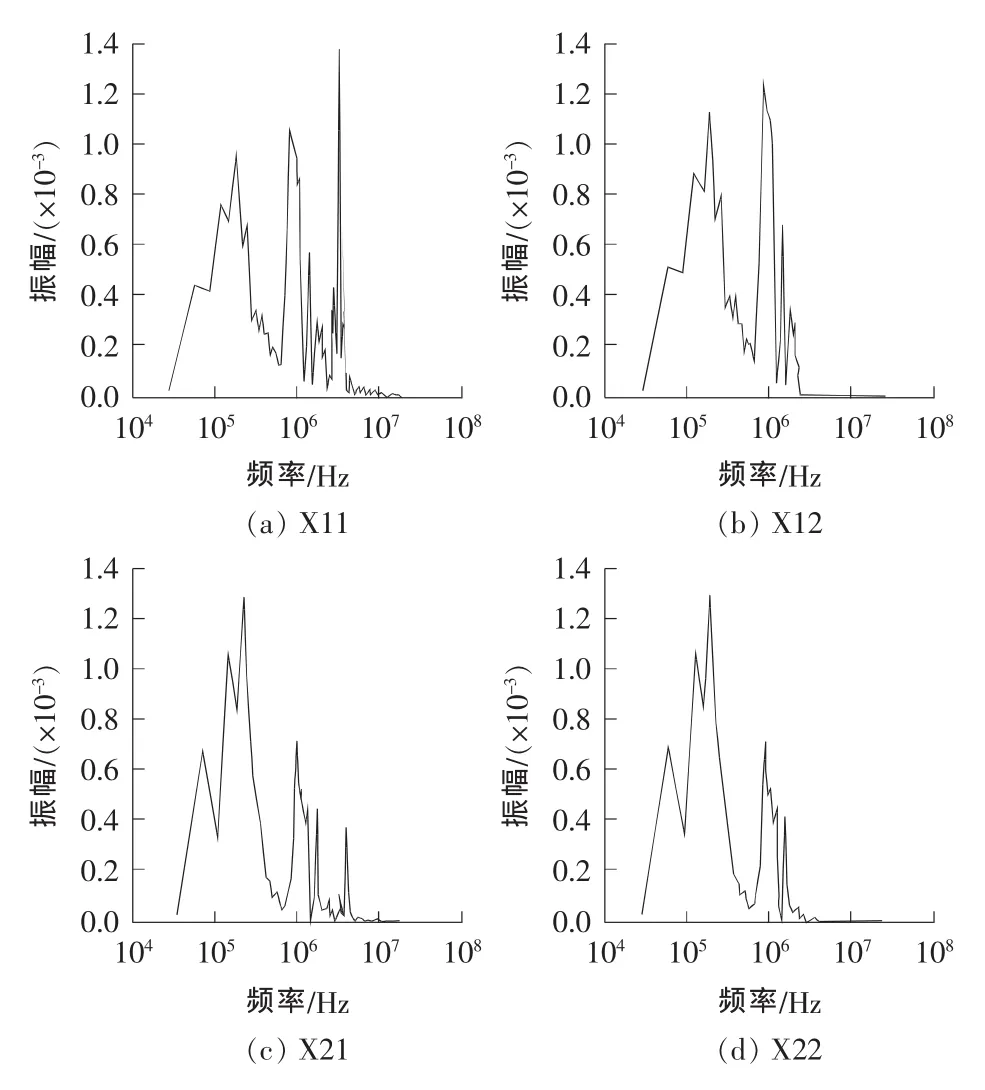
图6 图5中对应信号的频谱Fig.6 Spectrogram of the corresponding signal in Fig.5

4 结论

本研究提出了一种时空滤波方法RBPF，并对声发射信号进行去噪处理。通过合理选择模型参数，由实验结果验证了RBPF能够加强声发射信号的信噪比，并保留其主要频率成分。实验中还发现，冲击荷载作用下石灰岩最大振幅所对应的频率为0.15和1MHz，这对爆破与机械震动作用下的声发射监控有着重要的参考价值。

值得注意的是：论文研究模型最初来源于其他学者用来处理地震数据。由于考虑到声发射与地震波具有一些共通性，通过修正其模型参数，延伸到RBPF处理声发射信号中，并取得了不错的效果。然而，对声发射信号最优模型的建立和过程，噪声特征仍需作进一步的研究。

（

）：

［1］ Niri E D，Farhidzadeh A，Salamone S.Nonlinear Kalman filtering for acoustic emission source localization in anisotropic panels［J］.Ultrasonics，2014，54：486－501.

［2］ Baziw E，Jones I W.Application of Kalman filtering techniques for microseismic event detection［J］.Pure and Applied Geophysic，2002，159：449－471.

［3］ Zhang W M，Du G，Zhong S，et al.Study of nonlinear filter methods：Particle filter［J］.Journal of Systems Engineering and Electronics，2006，17（1）：1－5.

［4］ Petar M D，Jayesh H K，Zhang J Q，et al.Particle filtering［J］.IEEE Signal Processing Magazine，2003，20（5）：19－38.

［5］ Zhou C J，Zhang Y F.Particle filter based noise removal method for acoustic emission signals［J］.Mechanical Systems and Signal Processing，2012，28：63－77.

［6］ Menéndez R M，Freitas N，Poole D.Dynamic modelling and control of industrial processes with particle filtering algorithms［J］.Computer Aided Chemical Engineering，2004，18：721－726.

［7］ Freitas N.Rao－blackwellised particle filtering for fault diagnosis［J］.IEEE Aerospace Conference Proceedings，2002，4：1767－1772.

［8］ Mustière F，Bolic＇M，Bouchard M.Rao－Blackwellised particle filters：Examples of application［A］.IEEE CCECE／CCGEI［C］.Ottawa，Canada：［s.n.］，2006：1196－1200.

［9］ 潘宏侠，门吉芳.粒子滤波在轴承故障振动信号降噪中的应用［J］.振动、测试与诊断，2011，31（3）：354－356.（Pan Hong－xia，Men Ji－fang.Bearing fault vibration signal noise reduction based on particle filtering［J］.Journal of Vibration，Measurement ＆ Diagnosis，2011，31（3）：354－356.（in Chinese））