基于响应面法的斜拉桥静力体系可靠度

王 达，唐 浩，2

斜拉桥以其合理的结构形式、优美的外观及经济的造价等特点得到了迅速的发展和广泛的应用，成为大跨度桥梁的主要选型之一。在运营期间，由于拉索锈蚀、混凝土碳化、汽车超载以及不可预见的自然灾害等因素的影响，该类桥梁结构的安全储备将会逐渐降低，其安全性引起了人们的重视。目前，主要采用有限元等确定性分析方法，对该类桥梁结构进行安全分析。然而，实际工程存在诸多随机因素，如：混凝土主梁的容重和弹性模量等参数的随机性、斜拉索的材料变异性及索力的误差等，常规的确定性分析理论与方法不再适用于随机因素作用下大跨度预应力混凝土（The prestressed concrete，简称为PC）斜拉桥的安全分析。

以概率统计理论为基础的结构可靠度方法在考虑结构参数与荷载随机性的安全评估中得到了应用和发展。陈铁兵［1］基于响应面法（The response surface method，简称为RSM），分析了考虑结构几何非线性和参数随机性的斜拉桥在正常使用极限状态下的可靠度。程进［2］对比了拉索垂度效应、梁柱效应及大位移效应等几何非线性因素对静力可靠度的影响。然而，斜拉桥由斜拉索、主梁、索塔及辅助墩等多种构件和多种材料组成的超静定结构体系。在随机因素作用下，其失效模式较多，如：主梁弯曲失效、拉索强度失效及主梁跨中位移超限失效等，且单一的构件破坏并不致使结构体系的失效，结构体系表现出明显的失效历程。应用结构体系可靠度，可解决该类问题。刘扬［3］采用改进的β约界法，对一座跨径为460m的PC斜拉桥进行了施工期体系可靠度分析，构建了混凝土斜拉桥的主要失效树。但目前针对斜拉桥在运营期间的体系可靠度研究较少。

RSM以其对隐式功能函数重构的能力在结构可靠度分析中得到了广泛的应用，然而，在体系可靠度方面的应用较少。由于RSM可以给出结构的显式功能函数，由此得到各功能函数间的相关系数，因此可基于RSM对斜拉桥结构进行体系可靠分析。作者拟建立斜拉桥结构体系可靠度的数学模型，提出基于RSM的体系可靠度分析方法。以一座主跨420m混凝土斜拉桥为工程背景，展开体系可靠度分析，以期得出斜拉桥在随机荷载作用下混凝土斜拉桥的主要失效路径。

1 斜拉桥结构体系可靠度的数学模型

斜拉桥单个构件的失效概率计算和结构失效共（k－1）个 单 元 逐 个 失 效，Er（11），Er（22／）r1，…，E（k－1）rk－1／r1，r2，…，rk－2分别表示每个单元的失效事件。在第k阶段的失效过程中，单元rk的失效事件为E（k）r1k／r1，r2，…，rk－1。定义P（E（k）rk／）为失效事件E（k）rk／发生的概率，则其可靠指标为：路径的构建是斜拉桥体系可靠度分析的两个研究方面。与梁式桥相比，斜拉桥的功能函数是高次非线性的隐式函数，多个失效模式间具有一定的相关性。因此须基于失效概率计算和结构失效路径两个特征来建立其体系可靠度的数学模型。

1.1 结构体系的失效准则与搜索策略

Bruneau［4］采用主梁弯曲失效后增加塑性铰的方式实现结构体系转换的方法，对一座斜拉桥主梁的14种失效模式进行了分析。在实际工程应用中，若考虑到所有主梁的塑性铰，必然会有无数的失效路径，增加了体系可靠度分析的难度。事实上，斜拉桥主梁塑性铰的出现已经影响到斜拉桥的使用性能，即可认为结构体系的失效。另一方面，若索塔的某一截面形成塑性铰，也可认为结构体系失效。因此，本研究以主梁和主塔截面出现塑性铰的形式来判断结构体系的失效。

目前，广泛使用的失效模式搜索策略为Thoft－Christensen［5］提出的β约界法。假定：由n个单元组成的结构体系中，有r1，r2，…，rk－1

若定义β（mkin）＝min（βr（kk／）），则候选单元的条件为：

针对预应力混凝土斜拉桥，斜拉索失效后，直接删除失效单元，在混凝土主梁和索塔失效后，则认为结构体系失效。

1.2 主要失效模式的极限状态方程

承载能力极限状态下，斜拉桥分别由斜拉索的强度破坏和主梁塑性铰两种失效模式产生。由于索塔和主梁存在着较大的轴力，并直接影响其极限承载力，因此，应按压弯构件考虑。这两类失效模式的功能函数分别为：

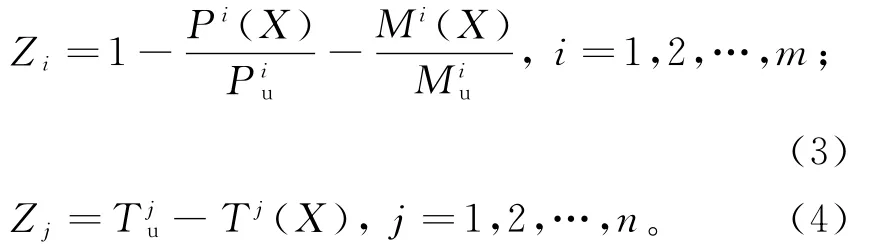
式中：X为随机变量；m和n分别为可能发生弯曲失效和拉索强度失效的单元数量；Piu和Miu分别为主梁或索塔第i个截面的轴力抗力和弯曲抗力；Pi（X）和Mi（X）分别为主梁或索塔第i个截面的轴力和弯矩作用效应值；Tju为第j根斜拉索的强度；Tj（X）为第j 根斜拉索的索力；Pi（X），Mi（X），Tj（X）和u（X）均为具有高次非线性的隐式函数，可以通过本研究提出的响应面法求解。

2 斜拉桥体系可靠度分析方法

考虑到斜拉桥可靠度模型的特点和影响结构受力状态的因素非常复杂，随机变量的输入与输出之间的关系是高度非线性的，在进行可靠度分析时，往往不能给出功能函数的明确表达式。在计算这类复杂结构的可靠度时，采用一次二阶矩阵法求解存在困难。而采用 Monte－Carlo抽样（MCS）无法直接求解失效概率较低的工程结构的可靠度。其次，斜拉桥具有高次超静定结构，其失效路径较为繁杂，构建完整的失效树较困难，且体系失效概率难以求解。针对这类问题，本研究拟采用基于二次序列响应面法和宽界限法，对斜拉桥进行体系可靠度分析。

2.1 结构构件可靠度求解

Bucher［6］最早提出了二次序列响应面法，然后将其应用于结构的可靠度分析中。二次序列响应面法应用于复杂结构可靠度分析中的优点是：具有将隐式功能函数显示化的能力，即可采用显式的函数表达式来表达结构的功能函数。基于二次序列响应面法的优点，本研究拟将其应用于斜拉桥结构体系可靠度中。其基本思路为：采用二次序列响应面方法，构建斜拉桥各个构件的隐式功能函数，然后由约束优化的方式搜索验算点，反复迭代，求解可靠指标。不含交叉项的二次响应函数表达式为：

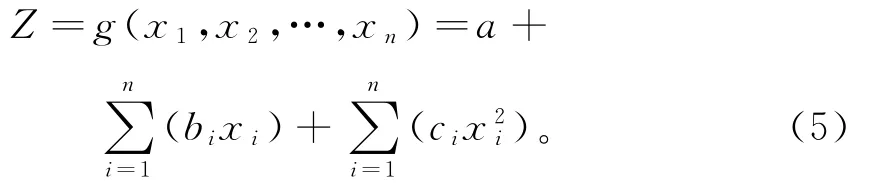
式中：xi为第i个随机变量；a，bi和ci均为待定系数（待定系数可能过2n＋1个样本点数据求解）。

得出显式的响应面函数后，即可采用约束优化方式求解可靠指标。优化函数为：

式中：xi为第i个随机变量；μ′xi和σ′xi分别为随机变量当量正态化后的均值和标准差。

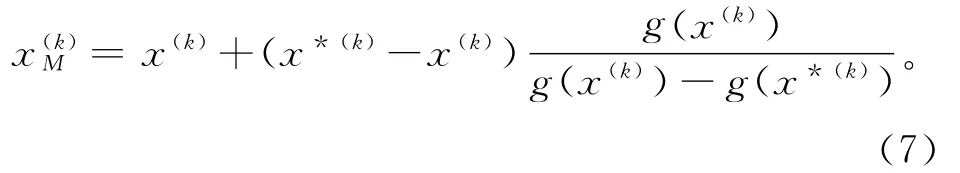
基于RSM和有限元方法，结构构件可靠指标求解步骤［7］为：

1）根据结构有限元模型内力分析结果，选取主要失效模式。

3）通过有限元方法，求解样本点处的功能函数样本值。

4）解线性方程组，得2n＋1个待定系数，由此得到响应面函数。

5）采用式（7）的约束优化方法，求得验算点x＊（k）和可靠指标β（k）。

6）验证β（k）是否满足计算精度，若不满足精度，则采用插值方式，得到新的验算点。

2.2 结构体系可靠度求解

在获得构件可靠度后，即可通过串、并联关系得到体系可靠指标。根据斜拉桥结构的受力特点，当主梁和索塔弯曲失效后，即认为结构体系失效；当拉索失效后，直接删除失效单元，进入下个阶段分析，直至结构体系失效。

通过分析主要失效模式并构建失效树［7］，得出连续刚构桥在运营期间的体系可靠度。然而，与连续刚构桥型相比，斜拉索在外界荷载作用下的失效路径更为繁杂。因此，在高效构建失效树方面，应做更多的研究工作。结构体系失效事件Es是由m 个独立的失效模式Ei（i＝1，2，…，m）导致的，Ei包含Eji（j＝1，2，…，n）共n 个相继失效状态。则体系可靠度表示为：

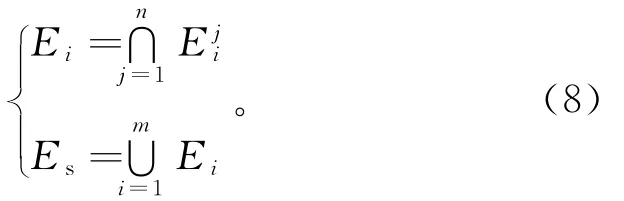
由式（8）可知，单个失效模式由各失效状态并联而成，而体系失效则由各失效模式串联而成。由于失效模式间具有一定的相关性，因此应分析各失效模式间的相关系数。考虑失模式间的相关性，在构建失效树时应将相关性高的失效状态归为一类，并选择最易失效的失效状态作为代表。针对宽界限法中存在的问题，采用Ditlevsen［8］提出的窄界限法，两个失效模式联合失效的可靠度为：

式中：σij为两个失效模式间的相关系数。

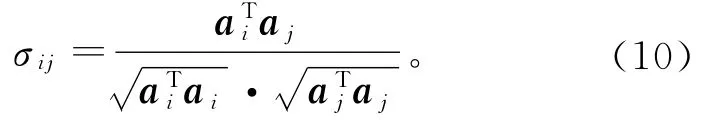
式中：ai和aj分别为两个功能函数在验算点处的方向余弦。

由式（5）和式（6）可重构出斜拉桥主要失效模式的功能函数表达式可靠指标；然后由式（10）计算两个功能函数间的相关系数，并得出相关系数矩阵；最后由式（9）和式（11）可得出斜拉桥的体系可靠指标。

3 工程实例

3.1 工程概况

合江长江二桥是泸渝高速公路上一座主桥跨径布置为210＋420＋210m的刚构体系双塔混凝土斜拉桥（如图1所示）。用C60混凝土作为主梁材料，用C50混凝土作为主塔材料，用钢绞线做斜拉索，每个塔均有34对拉索。桥面宽30m，双向六车道，公路－I级汽车荷载。

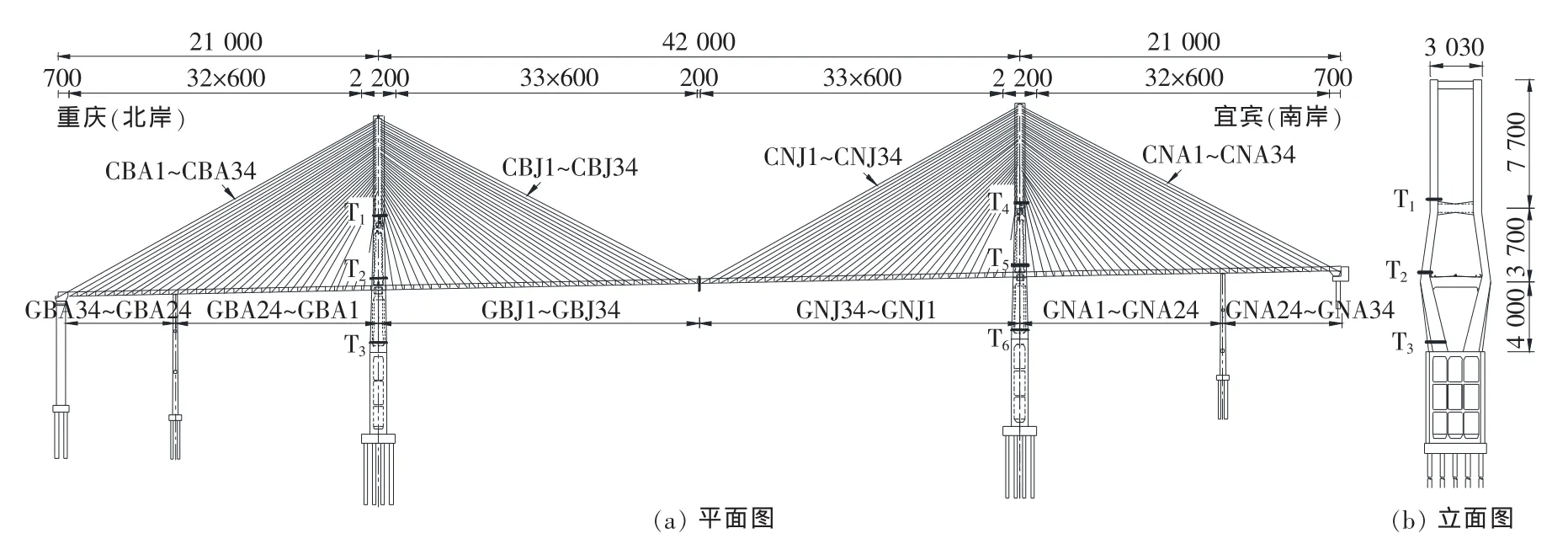
图1 合江二桥桥型布置及构件编号（单位：cm）Fig.1 The general arrangement diagram and series number of the second Hejiang Bridge（unit：cm）

从图1中可以看到各失效模式的关键失效位置编号。主梁单元编号为GBA1～GBA34，GBJ1～GBJ34，GNJ1～GNJ34和GNA1～GNA34；拉索单元编号为CBA1～CBA34，CBJ1～CBJ34，CNJ1～CNJ34和CNA1～CNA34；索塔单元编号为T1～T6。

钢绞线的屈服强度为σb＝1 860MPa。运营期的汽车荷载简化为中跨的均布荷载。随机变量X的统计参数见表1。

3.2 失效模式及相关参数

针对该斜拉桥具有隐式功能函数问题，要识别其主要失效模式和失效路径。与主梁和索塔等构件相比［9］，斜拉索具有较低的可靠指标，斜拉桥的可靠指标如图2所示。

由图2可知，可靠指标较低的斜拉索编号为CBA34和CBA33，其可靠指标分别为βCBA34＝4.84，βCBA33＝5.02，其响应面函数表达式分别为：

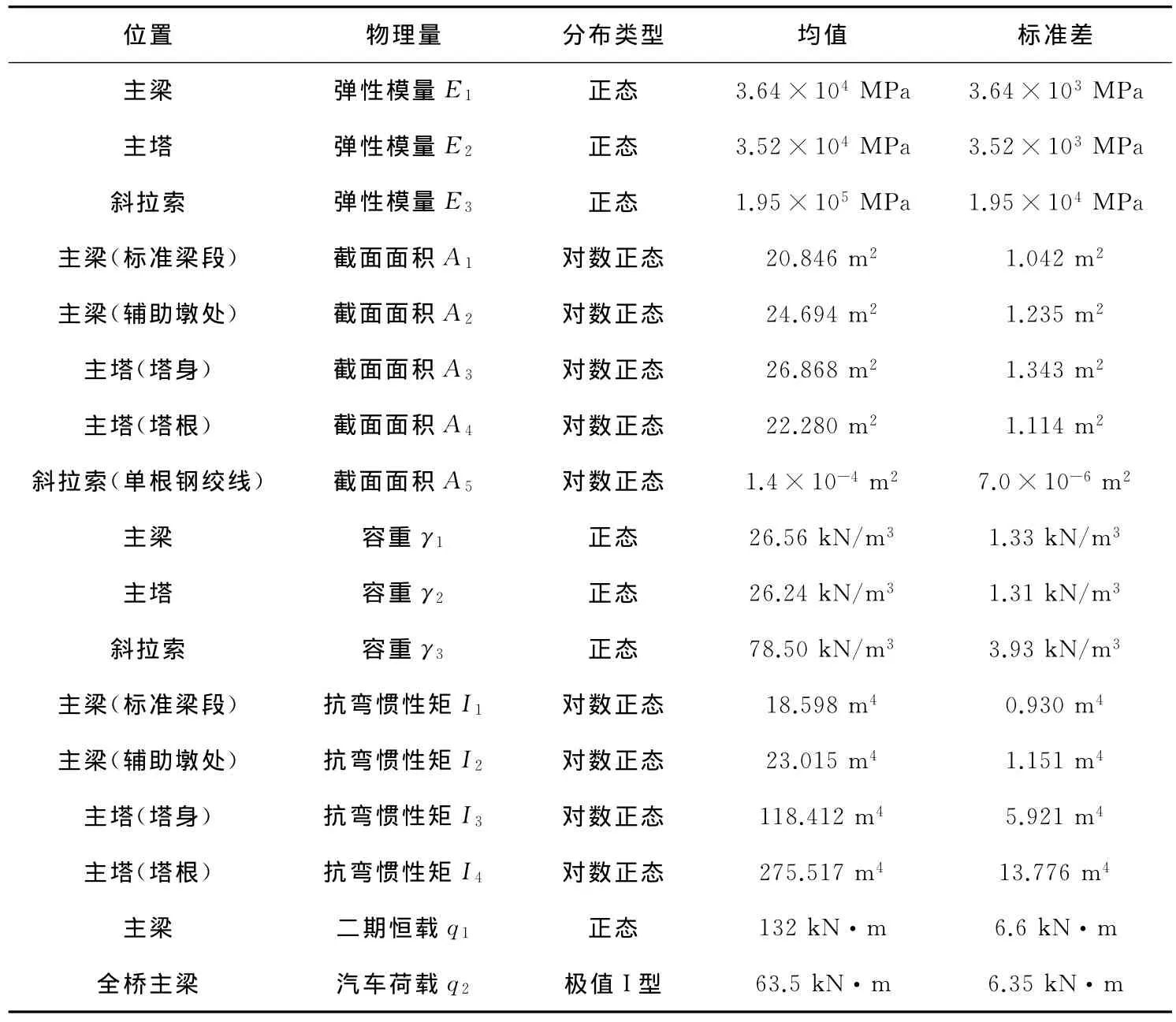
表1 合江二桥随机变量的统计参数Table 1 Statistic parameters of random variables for the second Hejiang Bridge

图2 斜拉索可靠指标Fig.2 Reliability index of cables

由式（10）可得出式（12）和式（13）相关系数为ρCBA34－CBA33＝0.93，其失效模式为高级相关，因此，选择CBA34为失效路径的第一层。在进行第二级失效路径搜索时，删除CBA34斜拉索。然后根据主梁和索塔的内力变化构建失效树，第二级失效路径构建时，主梁的可靠指标如图3所示。

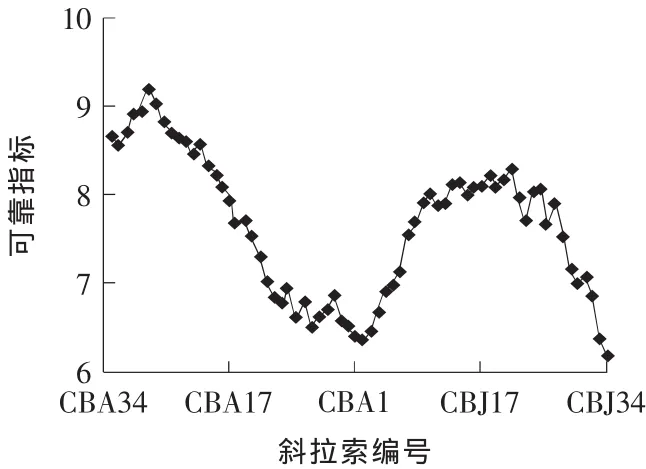
图3 删除CBA34号斜拉索后主梁的可靠指标Fig.3 Reliability index of girders under the failure of cables with series of CBA34

由图3可知，当CBA34号斜拉索失效后，塔梁交界处的主梁GBJ1和跨中主梁GBJ34的可靠指标最低，其可靠指标分别为βGBJ1＝6.34，βGBJ34＝6.17。因此，筛选该两个单元为候选失效单元。由于GBJ1号主梁为负弯矩失效，而GBJ34为正弯矩失效，因此该两个失效模式的相关性为低级相关。选取GBJ34号主梁的弯曲失效为代表失效模式。由此构建出的GBJ34号主梁弯曲失效的响应面函数表达式为：

由式（10）可得出式（12）和式（14）的相关系数为ρCBA34－GBJ34＝0.65，其相关性为低级相关。由式（9）和式（11）可得出由CAB34斜拉索强度失效后GBJ1号主梁和GBJ34号主梁弯曲失效这两条失效路径导致斜拉桥结构体系失效的可靠指标为βs＝4.69。

通过分析可知，影响斜拉桥体系可靠度的主要参数为主梁和斜拉索的弹性模量、主梁（标准段）的容重、主梁（标准段）和斜拉索的截面面积、主梁的容重和惯性矩、桥面二期恒载及汽车荷载，其他参数对可靠指标的影响较小，在响应面函数中已被略去。斜拉索端索的可靠指标与结构体系的可靠指标较为接近，斜拉索的安全性直接影响到斜拉索结构体系的安全性，因此，在运营期间，应对斜拉索进行定期检测和安全评估。

4 结论

针对斜拉桥静力体系可靠度分析中隐式功能函数重构和多种失效模式的特点，提出了一种基于响应面法的体系可靠度分析方法，并应用于主跨为420m的混凝土斜拉桥的体系可靠度分析。得出的结论为：

1）采用响应面法，得出斜拉桥多种失效模式的显式功能函数；然后，基于该显示功能函数，即可得到多种失效模式间的相关系数；最后，通过窄界限法，估算出体系的可靠指标，将响应面法成功地应用于斜拉桥体系可靠度分析中。

2）影响斜拉桥体系可靠度的主要参数为主梁和斜拉索的弹性模量、主梁（标准段）的容重、主梁（标准段）和斜拉索的截面面积、主梁的容重和惯性矩、桥面二期恒载及汽车荷载，其他参数对可靠指标的影响较小。

3）斜拉索是影响斜拉桥体系可靠度的主要构件，斜拉索端索的可靠指标较低，且与斜拉桥的体系可靠指标较为接近。

4）混凝土斜拉索的两个主要失效路径分别为斜拉索端索失效导致塔梁交界处主梁负弯矩失效和跨中主梁的正弯矩失效。

（

）：

［1］ 陈铁冰，王书庆，石志源.计入结构几何非线性影响时斜拉桥可靠度分析［J］.同济大学学报，2000，28（4）：407－412.（CHEN Tie－bing，WANG Shu－qing，SHI Zhi－yuan.Reliability analysis of cable－stayed bridges considering geometrical non－linearity［J］.Journal of Tongji University，2000，28（4）：407－412.（in Chinese））

［2］ 程进，肖汝诚.斜拉桥结构静力可靠度分析［J］.同济大学学报：自然科学版，2004，32（12）：1593－1598.（CHENG Jin，XIAO Ru－cheng.Static reliability analysis of cable－stayed bridges［J］.Journal of Tongji U－niversity：Natural Science，2004，32（12）：1593－1598.（in Chinese））

［3］ 刘扬，张建仁.混凝土斜拉桥施工阶段的体系可靠度［J］.中国公路学报，2006，19（5）：53－58.（LIU Yang，ZHANG Jian－ren.System reliability for concrete cable－stayed bridges during construction［J］.China Journal of Highway and Transport，2006，19（5）：53－58.（in Chinese））

［4］ Bruneau M.Evolution of system－reliability methods for cable－stayed bridge design［J］.Journal of Structure Engineering，1992，118（4）：1106－1120.

［5］ Thoft－Christensen P，Sørensen J D.Reliability of structural systems with correlated elements［J］.Applied Mathematical Modelling，1982，6（3）：171－178.

［6］ Bucher C G，Bourgund U.A fast and efficient response surface approach for structural reliability problems［J］.Structural Safety，1990，7（1）：57－66.

［7］ 刘扬，鲁乃唯.基于响应面法的连续刚构桥体系可靠度分析［J］.交通科学与工程，2010，26（4）：24－29.（LIU Yang，LU Nai－wei.Analysis on system reliability of rigid frame bridge based on response surface method［J］.Journal of Transport Science and Engineering，2010，26（4）：24－29.（in Chinese））

［8］ Ditlevsen O.Narrow reliability bounds for structural systems［J］.Journal of Structural Mechanics，1979，7（4）：453－472.

［9］ 朱劲松，肖汝诚，何立志.大跨度斜拉桥智能可靠度评估方法研究［J］.土木工程学报，2007，40（5）：41－48.（ZHU Jin－song，XIAO Ru－cheng， HE Li－zhi.Reliability assessment of large－span cable－stayed bridges based on artificial intelligence［J］.China Civil Engineering Journal，2007，40（5）：41－48.（in Chinese））