平板式移相变压器的磁场分析
2014-05-07王众赵镜红孙盼李兵
王众,赵镜红,孙盼,李兵
平板式移相变压器的磁场分析
王众,赵镜红,孙盼,李兵
(海军工程大学电气与信息工程学院,武汉 430033)
提出了一种应用于多脉波整流的移相变压器,该新型移相变压器采用直线电机结构,具有结构简单,易于制造等优点。介绍了其工作原理。在不考虑平板式移相变压器的纵向端部效应和横向端部效应的前提下,分析了平板式移相变压器的磁场分布,为以后平板式移相变压器的优化设计提供了依据。
多脉波整流 移相变压器 磁场 直线电机
0 引言
文献[1]对多脉波整流技术的现状做了详尽的介绍,总结了现有的多脉波整流技术在实际应用中存在的诸多不足。寻找一种低容量,可以交、直流侧电隔离的新型移相变压器拓扑是未来多脉波整流技术发展的一个方向。图1所示的平板式移相变压器就是一种新的移相变压器拓扑,它是基于直线感应电机的结构,稍作改进而来。因此需要对这种新型移相变压器的磁场分布进行计算,以便于以后进一步的研究。

图1 平板式移相变压器二维示意图
1 平板式移相变压器的工作原理
我们知道,通过向旋转感应电机的定子绕组供对称正弦三相电,其气隙中就会产生沿气隙方向旋转的旋转正弦磁场,然后转子绕组会产生正弦电流,从而受力旋转。如果对其转子堵转,引出转子绕组,会得到一个正弦的电压或者电流。如果把旋转电机从一半径剖开,展开成直线电机,同样的对其原边绕组供对称正弦三相电,它的气隙中会产生平移的幅值不变的正弦磁场,从而在次边绕组中会产生正弦电流。如图1所示的平板式移相变压器,对其原边绕组中的ABC三相施加对称的正弦三相电,其气隙中就会产生平移的正弦磁场,次边绕组中的六个绕组会感应出两组相位相差30°的三相电。
这种新型平板式移相变压器有着直线电机的结构,接线和绕组都比传统的旋转电机更加方便;同时能够做成方形结构,便于模块化,在需要大电压或大电流的时候,通过多个平板式移相变压器的串并联就能实现;它的初级铁心和次级铁心通过螺栓固定在一起,相对静止,因此它的气隙可以通过调整初级铁心和次级铁心间的垫片厚度就能调整气隙的大小,如果是旋转电机结构,这基本上是不可能的;另外通过对次边开槽数目的调整,可按需要制成用于任意脉波整流的移相变压器(图1是用于十二脉波整流的移相变压器)。
2 平板式移相变压器的物理模型
为了能够有效的使用麦克斯韦方程组分析该平板式移相变压器内部的电磁场,必须把开了槽的初级铁心用一光滑表面所代替,用一理想的无限薄的电流层来代替初级绕组中的电流,这个电流层用线电流密度表示。

图2 二维理想场模型
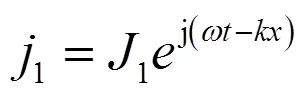
—电机极距;—电源角频率;1—初级绕组的相数;1——初级绕组每相串联匝数;w——初级绕组系数;1——初级绕组的极对数;1——初级相电流的有效值;



图3 多层通用模型
3 平板式移相变压器的电磁场方程式和解析解
为求得平板式移相变压器的电磁场,首先得对如图4所示的区域n的电磁场问题进行分析。
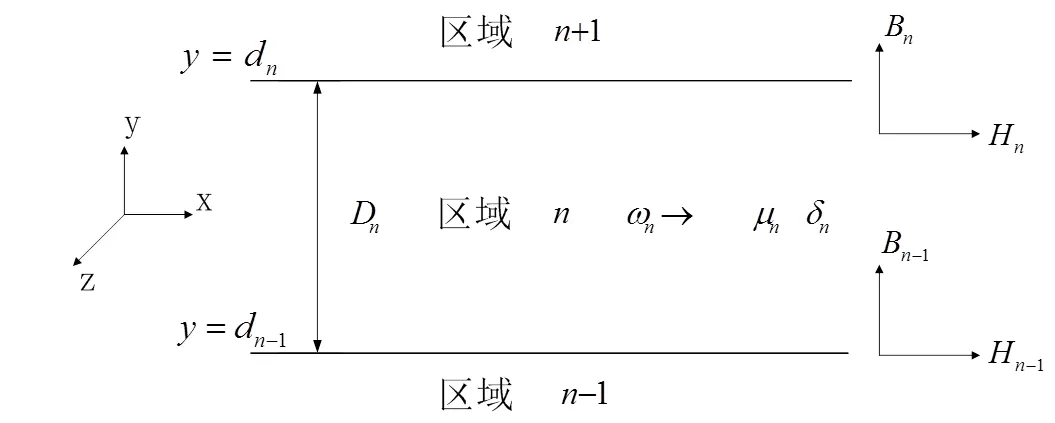
图4 区域n的通用模型


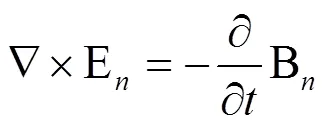




由式(1) ~ (3) 和式(6) 可以得到

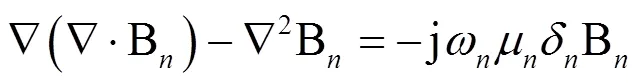
将式(4) 入式(8) 可得
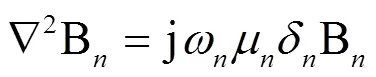
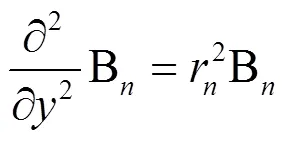
式中,

式中:n——电磁波的透入深度,
又因为B是和的函数。可以表示为

将式(11) 带入(10)得到


式中:B—B在坐标y上的分量;
B—B在坐标x上的分量。
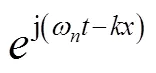

带入式(12) 中可求得

式中1、2——积分常数。
同理B可表示为

由磁场连续原理得

将式(15)和式(16)带入式(17)中,可得

由式(6) 和式(18)得

式中,

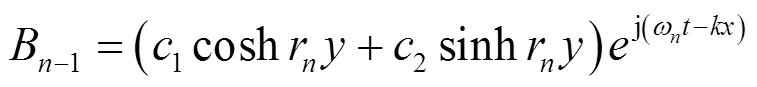

式(22) 和式(23) 可表示成矩阵形式


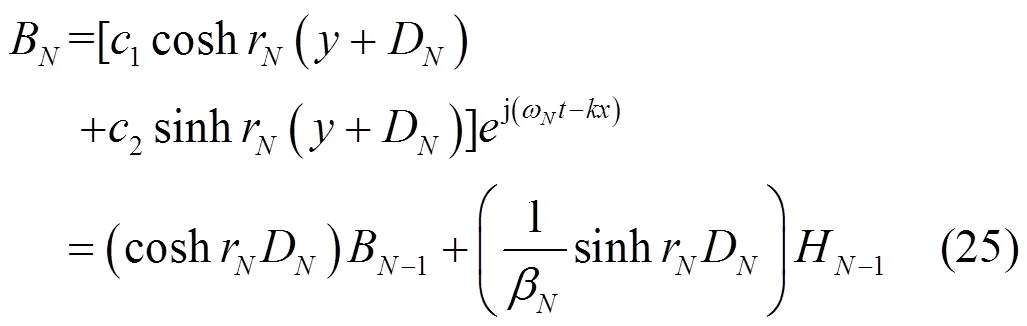
如果D趋于无穷大,则B趋于0,于是得
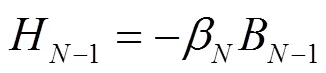
对于第1区域,有
(28)
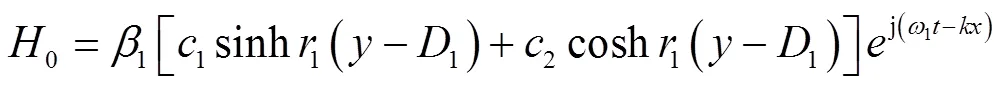
如果1趋于无穷大,0趋于0,于是得

由式(24) 考虑各个边界上的边界条件,可得到
于是由式(27) 、式(30) 、式(31)和式(32)求得1、1、r、r、N-1、N-1。再根据(24可求出图3中任意边界上的n和n。
4 结论
本文介绍了一种用于多脉波整流的新型移相变压器——平板式移相变压器,介绍了其工作原理并说明了其优点,在不考虑平板式移相变压器的纵向端部效应和横向端部效应的前提下,计算了平板式移相变压器的磁场分布n和n,为以后平板式移相变压器的优化设计提供了依据。
[1] 孟凡刚, 杨世彦, 杨威. 多脉波整流技术综述[J]. 电力自动化设备, 2012, 32(2): 9-22
[2] A.E. Fitzgerald, Charles Kingsley,Jr., Stephen D. Umans. Electric Machinery[M], Sixth Edition, 2004.
[3] 王铁军, 饶翔, 姜小弋等. 用于多重化逆变的移相变压器[J]. 电工技术学报, 2012, 27(6): 32-37.
[4] Jin Xu, Weiming Ma, Junyong Lu, et al. Analysis of magnetic field distribution and parameter calculation of linear induction motor with novel winding construction[C]. XIX ICEM Rome, 2010.
[5] 汤蕴璆, 梁燕萍. 电机电磁场的分析与计算[M]. 北京: 机械工业出版社, 2012.
[6] Nasar S A,Boldea I. Linear Motion Electric Machine [M]. New York: Wiley, 1976.
[7] 许金, 马伟明, 鲁军勇. 无槽双边长定子直线异步电动机二维磁场分布及电磁力计算[J]. 电工技术学报, 2008, 23(9): 38-44.
Field Analysis of Flat Phase-shifting Transformer
Wang Zhong, Zhao Jinghong, Sun Pan, Li Bing
(Naval University of Engineering, Wuhan 430033, China)
TM402
A
1003-4862(2014)12-0035-04
2014-05-08
王众(1989-),男,研究生。研究方向:电机与电器。
