基于SIFT特征匹配的图像拼接算法

廖 飞，叶玮琼，王鹏程，吴金津，许可可

（湖南工业大学 计算机与通信学院，湖南 株洲 412007）

基于SIFT特征匹配的图像拼接算法

廖 飞，叶玮琼，王鹏程，吴金津，许可可

（湖南工业大学 计算机与通信学院，湖南 株洲 412007）

针对传统图像拼接算法效率低和鲁棒性差的问题，提出一种改进的基于SIFT特征匹配的图像拼接算法。在图像预处理阶段，首次运用离散余弦变换、量化、反离散余弦变换、反量化，来对图像增强。其次，在计算变换模型时，由于没有预检验策略，致使RANSAC算法迭代次数增加。为此，提出了预检验策略。实验结果表明，在不改变匹配精度的前提下，该改进算法得到了比较理想的效果。

图像拼接；离散余弦变换；RANSAC算法；SIFT算法

0 引言

图像拼接是指将二幅或以上具有部分重叠的图像利用一定的图像拼接算法进行无缝拼接，得到一幅大型的无缝高分辨率宽视角图像。图像拼接可分为图像配准和图像融合两个步骤。图像配准是将不同时间、不同传感器（成像设备）或不同条件下（天候、照度、摄像位置和角度等）获取的两幅或多幅图像进行匹配、叠加的过程。图像融合是指综合和提取两个或多个多源图像信息，获得对同一场景或者目标更为准确、全面和可靠的图像，使之更适应于人眼感知或计算机后续处理。目前，图像融合技术在算法上已经相当成熟，对图像拼接的质量影响不大，图像配准的好坏直接关系到图像拼接的质量和效率，是图像拼接的关键[1]。尺度不变特征变换匹配算法[2]（scale invariant feature transform，SIFT）由于其对图像旋转和尺度变化等均具有不变性，是广泛使用的一种特征匹配算法。但是SIFT算法提取特征点后，必须消除不匹配点。传统的随机取样一致性算法[3]（random sample consensus，RANSAC）在消除过程中效率非常低，尤其当图像待匹配特征点中误匹配点比例较大时，耗时较多，大大影响了图像拼接算法效率。

针对传统图像拼接算法效率低和鲁棒性差的问题，课题组提出一种改进的基于SIFT特征匹配的图像拼接算法。在图像预处理阶段，首先，运用离散余弦变换、量化、反离散余弦变换、反量化对图像增强。其次，在计算变换模型时，由于没有预检验策略，致使RANSAC算法迭代次数增加。因此，提出了预检验策略，通过改进大大减少了算法迭代次数，提高了匹配效率。

1 图像预处理

为了剔除图像噪声和提升图像品质，要对原始图像和目标图像进行预处理操作。利用人眼对高频部分不敏感的特性，采用空间域的低通滤波器和量化过程实现图像数据优化处理。

1.1 离散余弦变换和反离散余弦变换

离散余弦变换（discrete cosine transform，DCT）实际上是空间域的低通滤波器，具有很强的“能量集中”特性。大多数自然信号（包括声音和图像）的能量都集中在离散余弦变换后的低频部分。

二维正向离散余弦变换F(u, v)（forward DCT，FDCT）计算公式如下（采用 8×8 图像块）：

式中：c(u)为第u个余弦变换系数；c(v)为第v个余弦变换系数；u，v为广义频率变量；f(i, j)为空间域中的二维向量；u, v, i, j=0, 1, 2,…, N-1。

当对图像解码时，使用反向离散余弦变换f(i, j)（inverse DCT，IDCT），变换公式如下：

二维离散余弦变换具有可分离性，所以二维变换可分解为一系列的一维变换G(i, v)。（行，列）计算公式如下：

1.2 量化和反量化

量化是在不引起明显的视觉效果失真的前提下，部分抛弃图像数据，以达到剔除图像中噪声的目的[4]。量化过程实际上是简单地把频率领域上的每个值，除以量化表中对应的常数，四舍五入取最接近的整数。整个量化的目的是减小非“0”系数的幅度以及增加“0”值系数的数目。

图像块（8×8）经过DCT变换后，低频分量都集中在左上角，高频分量分布在右下角。由于图像的主要信息包含在低频率分量中，而高频分量往往包含噪声信号，影响图像品质和数据优化处理，所以可以剔除高频分量。将高频分量去除就是量化，反量化是量化的逆过程。由于量化表左上角的值较小，右下角的值较大，这样就起到了保持低频分量和抑制高频分量的作用。

量化值计算公式如下：

式中：Sq(u, v)为量化后的结果；F(u, v)为DCT系数；S(u, v)为量化表中的数值。

图像预处理过程具体实现步骤如下：

Step1 将两幅图像进行离散余弦变换，把图像中点与点间的规律呈现出来；

Step2 进行量化处理，在高频段，将出现大量连续的零，这样就剔除了图像中的噪声；

Step3 进行反量化和反离散余弦变换，把图像从空间域变换到时间域，预处理过程结束。

2 算法流程

传统SIFT特征匹配算法可归为在不同尺度空间上查找特征点的问题。由于其具有很好的不变性，所以被广泛运用于图像的特征提取和匹配中，但是其提取出来的特征点往往包含着大量误匹配特征点对，因此，对其进行改进，添加预检验策略过程。

2.1 传统的SIFT特征匹配算法

1999年British Columbia大学大卫·劳伊（David G. Lowe）教授总结了现有的基于不变量技术的特征检测方法，正式提出了一种基于尺度空间的、对图像缩放、旋转甚至仿射变换保持不变性的图像局部特征描述算子SIFT[5]。

传统的SIFT算法具体实现步骤如下。

1）关键点检测。关键点是一些十分突出并且不会因光照条件的改变而消失的、在不同尺度空间的图像检测出的具有方向信息的局部极值点。

高斯核是唯一可产生多尺度空间的变换核[6]，一个函数的尺度空间L(x, y, )，定义为输入图像I(x, y)（代表图像在位置(x, y)的像素值）与一个可变尺度的二维高斯函数G(x, y, )卷积运算（ 为高斯正态分布标准差，称为尺度空间因子）。

为更有效检测出尺度空间中的稳定特征点和简化运算，引入高斯差分函数D(x, y, )（k为相邻两个图像的尺度比例因子的尺度）：

2）关键点描述。描述的目的是在关键点计算后，用一组向量将这个关键点描述出来，这个描述子不但包括关键点，也包括关键点周围对其有贡献的像素点。通过对关键点周围图像区域分块，计算块内梯度直方图，生成具有独特性的向量。

3）关键点匹配。分别对原始图像和目标图像建立关键点描述子集合。目标的识别通过两点集内关键点描述子的比对来完成。采用欧式距离作为具有128维的关键点描述子的相似性度量。即取一幅图像的一个特征点，找出另一幅图像中与其距离最近的前两个特征点，在这两个特征点中，若最近距离除以次近距离小于比例阈值，则接受该匹配点。

4）消除误匹配特征点。关键点匹配并不能标志算法结束，因为在匹配的过程中存在着大量的误匹配特征点。消除误匹配特征点，就要使用RANSAC算法。

2.2 改进的预检验策略

改进算法思想为：用RANSAC算法对误匹配特征点进行提纯时，因存在大量误匹配特征点，而RANSAC算法没有预检验策略，将在错误变换模型的计算和检验上耗费大量时间，致使其迭代次数增加、效率降低，并且影响拼接图像质量。为此，提出一种改进的预检验策略，在计算变换模型之前，用聚类法预筛选数据；再将筛选出来的数据用视差梯度法二次筛选，通过两次筛选大大减少了误匹配特征点对数目，提高了RANSAC算法效率。

2.2.1 预检验策略聚类法初次筛选

在运行RANSAC算法之前，根据待拼接图像匹配点之间的连线斜率应相同或相近的特性，将两幅待匹配的图像置于同一坐标系下，然后以某一斜率值为中心，设定一邻域阈值，依据以下特征找到某一较小邻域内包含最多的斜率相近点对，则这些点就是最精确匹配的相关点对。

定义如下特征来判断关键点是否是精确匹配的特征点对。

式中：ki，kj分别代表第i和第j条直线的斜率。

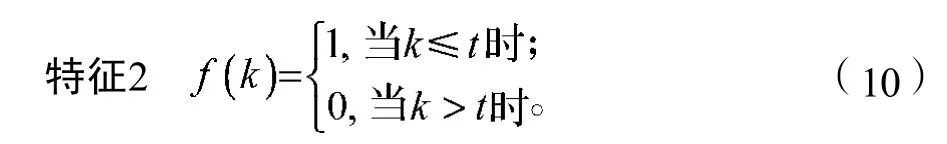
式中：t为邻域阈值（依据经验值本文取0.02）。

具体预检验策略实现步骤如下：

Step1 将原始图像和目标图像变换到同一坐标系下，计算粗匹配数据集中所有直线的斜率值；

Step2 由特征1和特征2循环计算值，并记下此时值，由此计算出邻域内的点对集，作为预选出的待匹配点，删除在邻域外的点对集；

Step3 如此循环，遍历整个粗匹配特征点集，得到初次筛选匹配特征点集。

2.2.2 预检验策略视差梯度法二次筛选

根据视差梯度的定义[7]，若原始图像中的两个相邻的特征点m，n分别和目标幅图像中的特征点m′，n′匹配，则视差梯度应小于2。采用视差梯度可以更精确地对特征点进行筛选，视差梯度的定义如特征3所示。

特征3 视差梯度Gd为

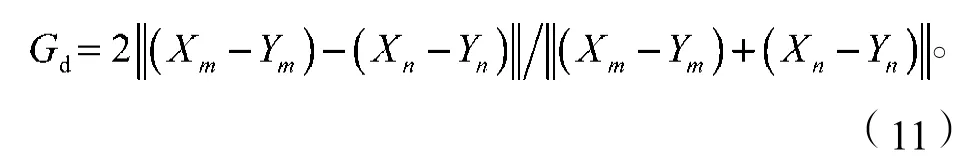
式中：（Xm, Ym）和（Xn，Yn）是对应特征点的图像坐标向量；·表示向量的模。

具体预检验策略实现步骤如下：

Step1 对2.2.1节筛选出的待匹配点集，从中随机选择两对匹配点，根据特征3计算它们的视差梯度值，若其视差梯度小于2，则接收该特征点对为精确匹配特征点对，否则剔除该点对；

Step2 如此循环，遍历所有特征点集，得到二次筛选匹配点集；

Step3 对筛选出来的匹配点集，再由RANSAC算法对其进行精确提纯，得到的结果集即为匹配的特征点对；

Step4 使用匹配的特征点计算变换矩阵，并用列文伯格-马夸尔特法[8]（levenberg-marquardt，LM）算法进行优化，最终完成特征匹配。

3 实验结果与分析

选择的实验平台为Visual C++6.0，改进图像拼接算法过程图如图1所示。

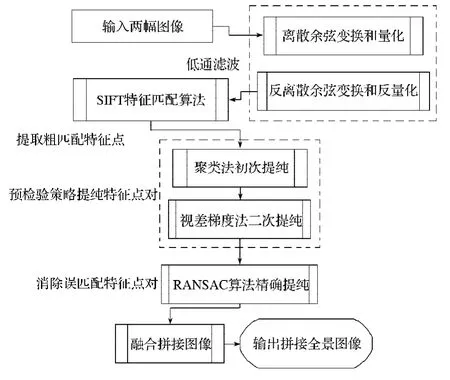
图1 图像拼接算法过程图Fig.1 The process of image stitching algorithm

为了更好地验证算法的有效性，选择2幅具有部分重叠区域的自然场景图像进行实验，图像如图2～3所示。

图2 待拼接图像1Fig.2 Original image 1

图3 待拼接图像2Fig.3 Original image 2

利用SIFT算法提取2幅图像的特征点并匹配，得到272个匹配点对。其结果如图4所示。由图4可以看出，对于图像的匹配结果存在误匹配现象。本研究组采用预检验策略和RANSAC算法对粗匹配点集进行提纯，删除误匹配特征点，对于同一图像得到筛选后的匹配点92对。最后，图像拼接后的效果图如图5所示。

图4 SIFT特征提取与匹配Fig.4 SIFT features extracting and matching

图5 图像拼接后的效果图Fig.5 The result of images stitching

通过和原算法比较，得到的对比结果如表1所示。

表1 改进算法与原算法对比Tabel1 The improved algorithm comparing with the original algorithm

从表1可以看出，改进算法一方面所用时间有所减少（其中包括预检验策略消耗的时间）、迭代次数明显降低；另一方面，用预检验策略剔除误匹配点时，消耗了大量时间，并且增加了算法复杂度。

4 结语

基于SIFT特征匹配的图像拼接算法，弥补了传统图像拼接方法在尺度、光照变化上的缺陷，但是该算法提取出来的粗匹配特征点包含大量误匹配特征点对，影响匹配效率。因此，提出两点改进之处：在SIFT算法之前，加入低通滤波器，使用量化过程剔除图像中的噪声，使图像增强；在运行RANSAC算法之前，用预检验策略筛选特征点集。实验结果表明，在不改变匹配精度的前提下，该改进算法效率更高。

[1] 张 琳，褚龙现. 基于全局拼接的船舶图像拼接算法研究[J]. 计算机仿真，2012，29(4)：282-285. Zhang Lin，Chu Longxian. Aerial Image Mosaic AlgorithmsResearch Based on Global Mosaic[J]. Computer Simulation，2012，29(4)：282-285.

[2]Brown M，Love D. Recognizing Panoramas[C]//Proceeding of the 9th International Conference on Computer Vision. Nite：[s.n.]，2003：218-225.

[3]Chen Fuxing，Wang Runsheng. Fast RANSAC with Preview Model Parameters Evaluation[J]. Journal of Software，2005，16(8)：1431-1437.

[4]张春田，苏育挺，张 静. 数字图像压缩编码[M]. 北京：清华大学出版社，2006：68-70. Zhang Chuntian，Su Yuting，Zhang Jing. Digital Image Compression Coding[M]. Beijing：Tsinghua University Press，2006：68-70.

[5] 曹 楠，王 萍. 基于SIFT特征匹配的图像无缝拼接算法[J]. 计算机与应用化学，2011，28(2)：242-244. Cao Nan，Wang Ping. Seamless Image Stitching Based on SIFT Feature Matching[J]. Computers and Applied Chemistry，2011，28(2)：242-244.

[6] Koenderink J J. The Structure of Images[J]. Biological Cybernetics，1984，50：363-370.

[7]马颂德，张正友. 计算机视觉[M]. 北京：北京科学出版社，1988：82-83. Ma Songde，Zhang Zhengyou. Computer Vision[M]. Beijing：Beijing Science and Technology Press，1988：82-83.

[8]Richard Szeliski，Hung-Yung Shum. Creating Full View Panoramic Image Mosaics and Environment Maps[C]// Proceeding of 24th Annual Conference on Computer Graphics and Interactive Techniques，Los Angels：ACM Press，1997：251-258.

（责任编辑：申 剑）

Image Mosaic Algorithm Based on SIFT Feature Matching

Liao Fei，Ye Weiqiong，Wang Pengcheng，Wu Jinjin，Xu Keke
（School of Computer and Communication， Hunan University of Technology，Zhuzhou Hunan 412007，China）

In order to solve the problem of low efficiency and poor robustness of traditional image mosaic algorithm, an improved SIFT-based feature matching algorithm for image stitching were put forward. Firstly enhanced the images by using the discrete cosine transform，quantization, inverse discrete cosine transform and inverse quantization in the image preprocessing stage, and then proposed the pre-inspection strategy in view of the RANSAC algorithm iteration increasing when computing the transformation models. The experimental results showed that the improved algorithm obtained the quite ideal effect without changing the matching precision.

image mosaic；discrete cosine transform；RANSAC algorithm；SIFT algorithm

TP317.4

：A

：1673-9833(2014)01-0071-05

2013-10-18

廖 飞（1988-），男，湖南常德人，湖南工业大学硕士生，主要研究方向为嵌入式系统，

E-mail ：1525127621@qq.com

10.3969/j.issn.1673-9833.2014.01.015